탐색과 이진탐색 (Binary Search)

먼저 탐색이란 주어진 자료에서 원하는 값을 찾는 작업, 즉 '검색'이다. 영어로도 'search'라고 한다.

탐색의 가장 단순한 방법은 리스트를 처음부터 마지막까지 하나씩 검사하며 내가 찾는 정보가 있는지 확인하는 '순차탐색'이 될 것이다. 하지만 이 방법은 최악의 경우 모든 데이터를 다 도는 $O(n)$의 시간복잡도를 가진다.

이진탐색이란 정렬된 리스트에서 특정 값을 빠르게 찾는 알고리즘이다. '이진'이란 키워드가 힌트하듯이 반으로 나누는 방식을 사용하여 탐색 범위를 점점 줄여 나가는 방법이다. 반으로 나누는 방식을 이전에 퀵정렬에서 분할정복 알고리즘을 통해 배운 바 있다. 분할정복 알고리즘은 문제를 더 작은 부분 문제로 분할하여 탐색의 범위를 좁힌 후 각 부분 문제를 재귀적으로 해결하며 정복해서 해답을 구하는 방식이다.

이진탐색의 원리

이진탐색의 원리를 알아보자.

1. 분할: 탐색 범위를 절반으로 나눈다. 이때 절반으로 나누는 기준은 리스트의 중간 값을 기준으로, 찾는 값 < 중간 값이면 왼쪽 리스트, 찾는 값 > 중간 값이면 오른쪽 리스트만 남긴다.

2. 정복: 중앙에 위치한 값과 찾는 값을 비교하여 분할하는 과정을 반복해가며 탐색 범위를 좁혀나간다.

3. 결합: 정렬에서는 리스트 전체를 정렬하는게 목적이었으므로 사혼의 구슬마냥 쪼개진 리스트들을 다시 붙이는 단계가 필요했는데, 이진탐색은 찾는 값이 발견되면 반환만 하면 되기 때문에 결합 단계는 필요없다.

여기서 중요한 점은 이진탐색은 리스트가 정렬되어 있다는 가정 하에 진행된다. 즉 실제로 코드로 구현할 때는 리스트를 정렬하는 작업이 먼저 필요하다.

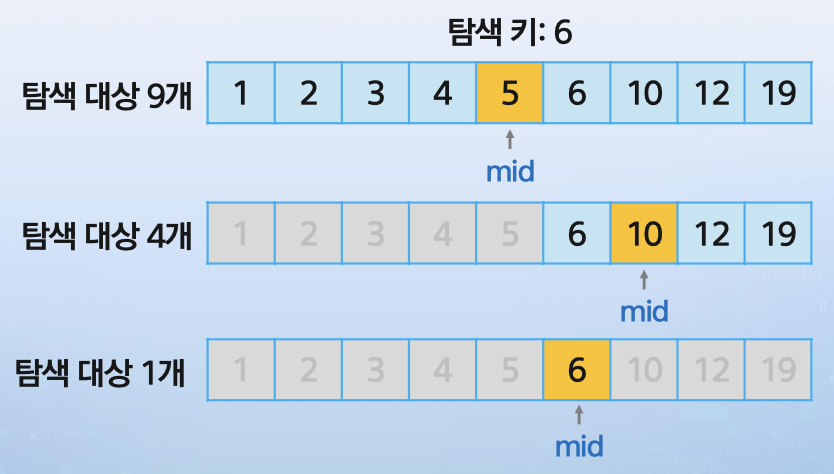
예시를 살펴보자.
여기서 찾아야 할 값은 6이다.
먼저 리스트 전체의 중간값은 5이다.
5와 6을 비교했을 때 6이 더 크므로 다음 탐색 대상은 5의 오른쪽 리스트가 된다.
그 다음 중간값은 10인데 6이 더 작다. 그러므로 왼쪽 리스트만 남는데 10의 왼쪽은 6뿐이므로 벌써 타겟을 찾았다.

시간복잡도 $O(logn)$

첫번째 탐색에서 데이터의 크기는 n이다.
그 다음 리스트를 절반으로 나누면 $n/2$이다.
이걸 계속 쪼개다가 k번째 탐색에서는 $n/2^k$이 된다.
마지막에 탐색이 완료되었을 때는 찾는 값 하나만 남게 되므로 $n/2^k=1$이 된다. 즉 $logn=k$가 되므로 입력 크기가 n일 때 k번 탐색하면 $O(logn)$의 시간복잡도를 가지게 된다.

장단점

이진탐색의 장점으로는 O(logn)인만큼 큰 데이터셋에서도 빠르게 값을 찾을 수 있다는 효율성과, 동작의 단순성이다.
하지만 단점으로는 정렬된 리스트에만 적용 가능하고, 그렇기 때문에 데이터를 추가하거나 삭제하기 어렵다는 점이다.

이진탐색 구현하기

예시를 통해 좀 더 자세히 이진탐색이 어떻게 동작하는지 살펴보자.
이진탐색에는 low, mid, high 세 개의 인덱스가 필요하다.
초기 mid는 (low+high)//2로 구한다.

mid와 찾는 값(x)을 비교해서

• mid와 찾는 값이 같다면 mid를 최종 값으로 반환한다.
• mid < x 라면 low = mid+1로 업데이트한다. (x가 mid보다 오른쪽 리스트에 있을 것이기 때문)
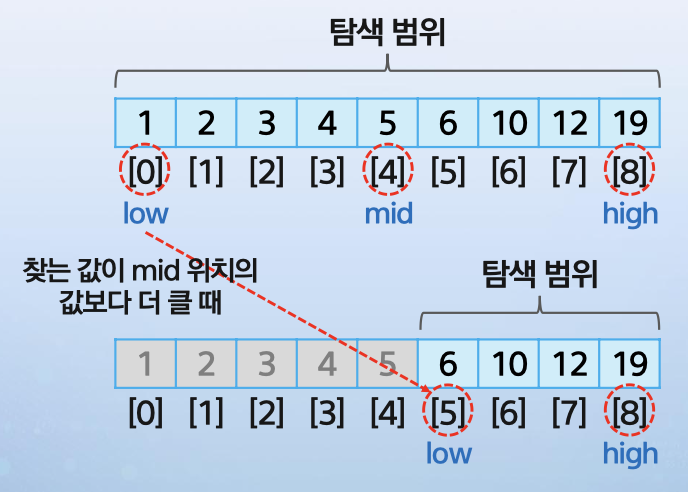  low = 4+1 = 5 가 된다. 이때 탐색 범위는 5~8로 축소된다.
• mid > x 라면 high = mid-1로 업데이트한다.(x가 mid보다 왼족 리스트에 있을 것이기 때문)
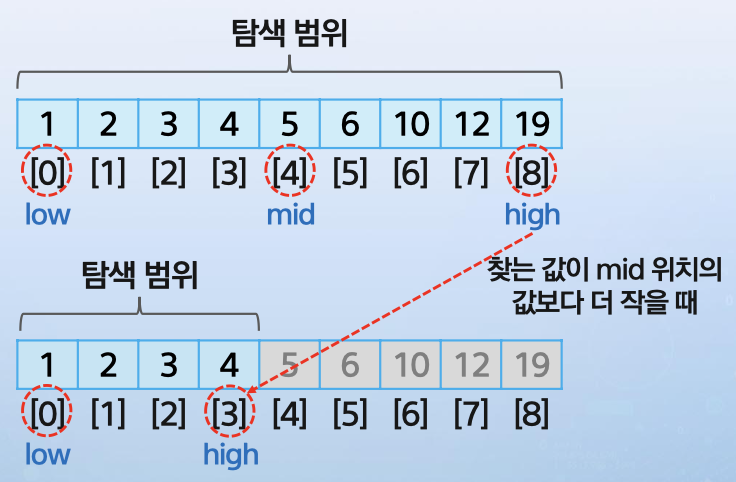  high = 4-1 = 3이 된다. 탐색 범위는 0~3으로 축소된다.

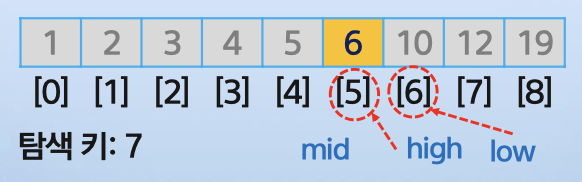
<탐색 실패하는 경우>
찾는 값이 없다면 탐색에 실패한다.
이건 어떻게 아느냐 -> 탐색 범위가 계속 좁혀지다가 low > high가 되면 찾는 값이 리스트에 없다는 뜻이므로 탐색 과정을 종료한다.
이때 종료 시점의 low 위치는 찾는 값을 삽입할 수 있는 위치가 될 수도 있다.

코드

이진탐색은 반복문과 재귀함수 두 가지 방식으로 구현할 수 있다.

1. 반복 (while문)

def binary_search_iterative(arr, x): 
	low = 0
    high = len(arr) – 1 
    while low <= high:				# 반복의 조건이다. 만약 low > high가 되면 반복문을 종료하고 탐색에 실패했으므로 None을 반환한다. 
		mid = (high + low) // 2 
        if arr[mid] == x:			# x의 위치를 찾음. 
			return mid 
       	elif arr[mid] < x:
			low = mid + 1 
		else :
			high = mid – 1 
	return None

2. 재귀

def binary_search_recursive(arr, low, high, x):
	if high >= low:		# 탐색이 계속 가능한 조건일 때는 재귀함수를 호출하게 된다. 
    	mid = (high+low)//2
        if arr[mid] == x:
        	return mid
       	elif arr[mid] > x: # x가 mid보다 작으면 탐색 범위를 mid의 왼쪽으로 줄여야 하므로 high 자리에 mid-1을 넣어준다. 
        	return binary_search_recursive(arr, low, mid-1, x)		
        else:
        	arr[mid] < x: # x가 mid보다 크면 탐색 범위를 mid의 오른쪽으로 줄여야 하므로 low 자리에 mid+1을 넣어준다. 
            	return binary_search_recursive(arr, mid+1, high, x)