모델 규제하기

Contents

1. Ridge Regression
2. Lasso Regression
3. Elastic Net Regression

회귀 알고리즘은 보통 비용 함수의 값을 최소화 하는
방향으로 학습을 합니다.

회귀 알고리즘의 학습에 사용되는 특성의 갯수가 많아질수록
과대적합 문제가 나타나게 됩니다.

과대하게 학습을 한 머신러닝 모델은 절대로 테스트 세트에 대한
점수를 높게 받을 수 없습니다.

아래의 그림은 과소적합과 과대적합을 나타낸 그림입니다.

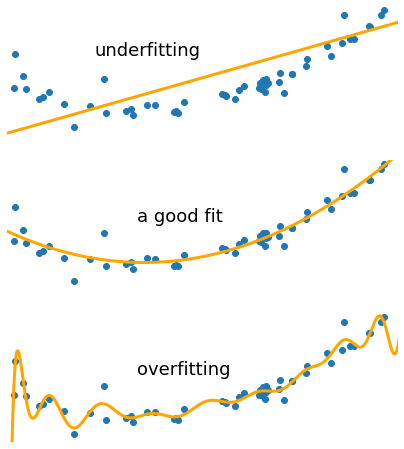
과대 적합이 왜 문제가 되는지 확실히 눈에 보입니다.

# 01 - Ridge Regression

릿지 회귀는 모델의 비용함수에 L2-norm 규제항을 추가합니다.
이때 규제항을 추가한 비용함수는 미분 가능하여 경사하강법을 사용할 수 있습니다.

릿지 회귀 모델의 비용함수는 다음과 같습니다.

$MSE(\theta) + \lambda\displaystyle\sum_{i=1}^{n}{\theta_{i}}^{2}$

위와 같이 비용함수에 규제항(L2-norm의 제곱) 을 추가한 모습입니다.
이때 $\lambda$가 바로 하이퍼파라미터 입니다.
$\lambda$의 값을 통해서 규제의 강도를 정할 수 있습니다.

# 02 - Lasso Regression

라쏘 회귀는 모델의 비용함수에 L1-norm 규제항을 추가합니다.
라쏘 회귀는 미분이 불가능 하여 Numerical optimization methods 들을 사용합니다.

라쏘 회귀 모델의 비용함수는 다음과 같습니다.

$MSE(\theta) + \lambda\displaystyle\sum_{i=1}^{n}{\vert\theta_{i}\vert}$

위와 같이 비용함수에 규제항(L1-norm) 을 추가한 모습입니다.
릿지 회귀와 마찬가지로 $\lambda$는 하이퍼파라미터 입니다.

라쏘 회귀는 릿지 회귀와는 다르게 중요하지 않은 가중치(비용 함숫값이 큰 특성)는
0 으로 만들어 버립니다. 이 점이 라쏘 회귀의 특징이자 단점입니다.
가중치를 0으로 만들어버리기 때문에 데이터 손실이 일어나서 정확도가 떨어질 수 있습니다.

위와 같은 라쏘 회귀의 특징 때문에 중요한 특성들이 많을 때에는
릿지 회귀를 사용하는게 좋고 중요한 특성들이 별로 없을 때에는
라쏘 회귀를 사용하는게 좋습니다.

릿지 회귀 또한 라쏘 회귀와는 다르게 상관관계가 높은 특성들을
선택하지 못한다는 단점이 존재합니다.

# 03 - Elastic Net Regression

릿지 회귀와 라쏘 회귀의 장점들은 모은 규제 알고리즘이 바로
Elastic Net 입니다.

Elastic Net 의 비용함수는 다음과 같습니다.

$MSE(\theta) + \lambda_{1}\displaystyle\sum_{i=1}^{n}{\theta_{i}}^{2} + \lambda_{2}\displaystyle\sum_{i=1}^{n}{\vert\theta_{i}\vert}$

역시 비용함수의 L1-norm과 L2-norm의 제곱을 더해준 것을 확인할 수 있습니다.
Elastic Net은 상관관계가 높은 특성들을
동시에 선택할 수 있다는 장점을 가지고 있습니다.

Elastic Net은 하이퍼 파라미터가 두개 입니다.
보통 이 두개의 하이퍼 파라미터는 그리드 서치를 이용하여 찾습니다.

이때 $\lambda_{1}=1$ 이면 Ridge 회귀 $\lambda_{2}=1$ 이면 Lasso 회귀 입니다.