
github url: https://github.com/EojinK/KU_DeeplearningAssignment1
In this assignment, I implemented 2-Layer Neural Net with Sofmax Classifier. I Performed the image classification using “CIFAR-10” dataset.
• Two weights W1, W2 with biased b1, b2.
• Predicted output y' = W2 relu W2x + b1 + b2.
• Total loss = data loss (softmax+log likelihood loss) + L-2 regularization loss (to W1, W2, not b1, b2).
1. description of my code
a) neural_net.py
#############################################################################
# TODO: Perform the forward pass, computing the class scores for the input. #
# Store the result in the scores variable, which should be an array of #
# shape (N, C). #
#############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
z1 = X.dot(W1) + b1
a1 = np.maximum(0, z1)
scores = a1.dot(W2) + b2
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# ... 중략
#############################################################################
# TODO: Finish the forward pass, and compute the loss. This should include #
# both the data loss and L2 regularization for W1 and W2. Store the result #
# in the variable loss, which should be a scalar. Use the Softmax #
# classifier loss. #
#############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# scores
a2 = np.exp(scores) / np.sum( np.exp(scores), axis=1, keepdims=True )
# softmax loss
loss = ( np.sum(-np.log(a2[range(N), y])) / N ) + ( reg * (np.sum(W1 ** 2) + np.sum(W2 ** 2)) )
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# ... 중략
#############################################################################
# TODO: Compute the backward pass, computing the derivatives of the weights #
# and biases. Store the results in the grads dictionary. For example, #
# grads['W1'] should store the gradient on W1, and be a matrix of same size #
#############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
dscores = a2
dscores[range(N), y] -= 1.0
dscores /= N
dhidden = np.dot(dscores, W2.T) * (z1 > 0)
grads['W2'] = np.dot(a1.T, dscores)
grads['b2'] = np.sum(dscores, axis=0)
grads['W1'] = np.dot(X.T, dhidden)
grads['b1'] = np.sum(dhidden, axis=0)
grads['W2'] += reg * W2
grads['W1'] += reg * W1
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# ... 중략
#########################################################################
# TODO: Create a random minibatch of training data and labels, storing #
# them in X_batch and y_batch respectively. #
# - See [ np.random.choice ] #
#########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
random_indices = np.random.choice(num_train, batch_size)
X_batch = X[random_indices]
y_batch = y[random_indices]
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# ... 중략
#########################################################################
# TODO: Use the gradients in the grads dictionary to update the #
# parameters of the network (stored in the dictionary self.params) #
# using stochastic gradient descent. You'll need to use the gradients #
# stored in the grads dictionary defined above. #
#########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
self.params['W2'] -= learning_rate * grads['W2']
self.params['b2'] -= learning_rate * grads['b2']
self.params['W1'] -= learning_rate * grads['W1']
self.params['b1'] -= learning_rate * grads['b1']
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# ... 중략
###########################################################################
# TODO: Implement this function; it should be VERY simple! #
# perform forward pass and return index of maximum scores #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
a1 = np.maximum(0, np.dot(X, self.params['W1']) + self.params['b1'] )
scores = np.dot(a1, self.params['W2']) + self.params['b2']
y_pred = np.argmax(scores, axis=1)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****In neural_net file, I put z1 as a pre-activation of first layer(z = wx + b), a1 as an activation of first layer, scores as a pre-activation of second layer. I builded a2 value (regularization of W1 and W2 data) and loss value (with softmax). To compute backward pass, I made dscores and hidden values that can be used in grads dictionary. I created X_batch, y_batch and stored random indices with function np.random.choice(). Using stochastic gradient descent, I updated gradients from W2 to W1, from b2 to b1. Finally, I put a1, scores, y_pred to final predict result.
b) Hyperparameter tuning in two_layer_net.ipynb
best_net = None # store the best model into this
#################################################################################
# TODO: Tune hyperparameters using the validation set. Store your best trained #
# model in best_net. #
# #
# To help debug your network, it may help to use visualizations similar to the #
# ones we used above; these visualizations will have significant qualitative #
# differences from the ones we saw above for the poorly tuned network. #
# #
# Tweaking hyperparameters by hand can be fun, but you might find it useful to #
# write code to sweep through possible combinations of hyperparameters #
# automatically like we did on the previous exercises. #
#################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
best_val = -1
best_stats = None
learning_rates = [1e-2, 1e-3, 1e-4]
regularization_strenghts = [0.3, 0.4, 0.5]
iters = 2000
results = {}
for lr in learning_rates:
for rs in regularization_strenghts:
net = TwoLayerNet(input_size, hidden_size, num_classes)
stats = net.train(X_train, y_train, X_val, y_val,
num_iters=iters, batch_size=200,
learning_rate=lr, learning_rate_decay=0.95,
reg=rs, verbose=False)
y_train_pred = net.predict(X_train)
train_acc = np.mean(y_train == y_train_pred)
y_val_pred = net.predict(X_val)
val_acc = np.mean(y_val == y_val_pred)
results[lr, rs] = train_acc, val_acc
if best_val < val_acc:
best_stats = stats
best_val = val_acc
best_net = net
for lr, rs in sorted(results):
train_accuracy, val_accuracy = results[(lr, rs)]
print('lr: %e rs: %e train accuracy: %f val accuracy: %f' % (
lr, rs, train_accuracy, val_accuracy))
print('best validation accuracy: %f' % best_val)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****In hyperparameter tuning part, I tried to find the optimal learning rate and regularization strengths. The learning rates I tested were 1e-2, 1e-3, 1e-4 and the regularization strenghts were 0.3, 0.4, 0.5. I used a for loop to test all cases. I applied each parameter to TwoLayerNet and stored the highest accuracy in the best_val variable.
2. results
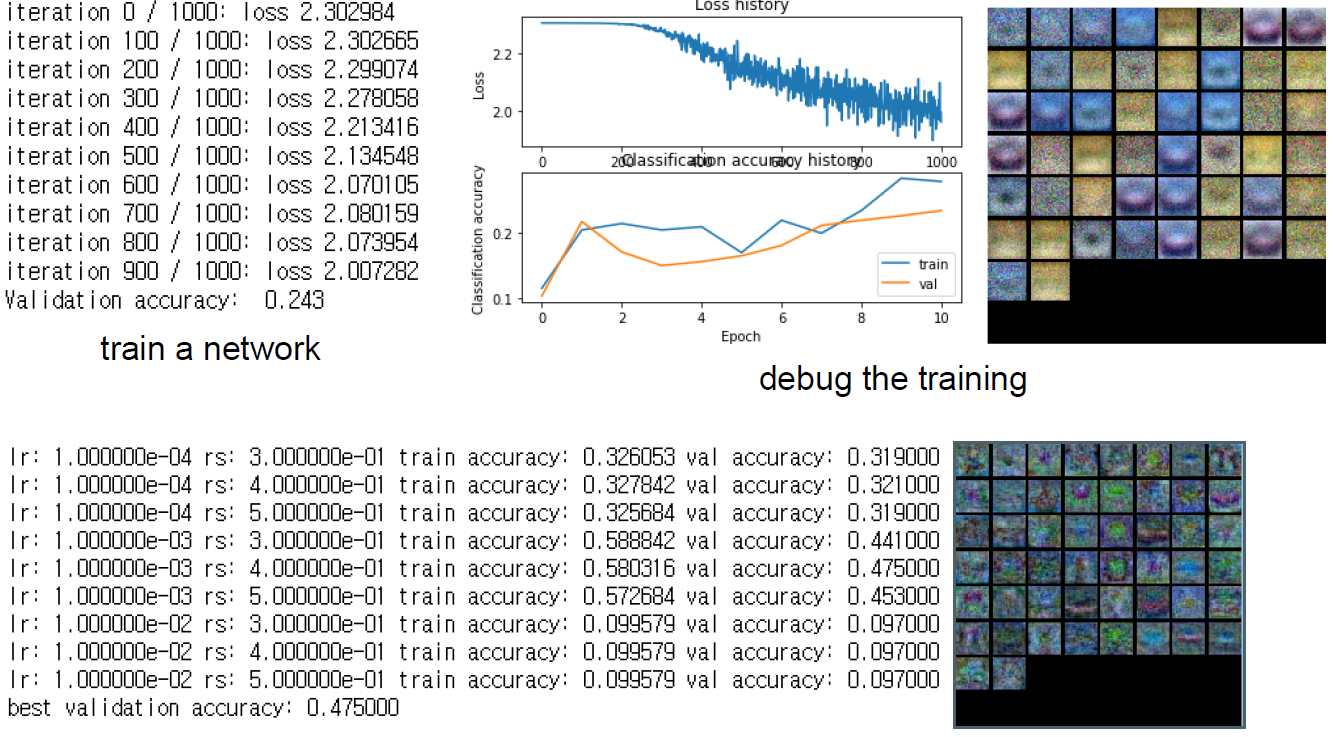
3. Discussion
My optimal hyperparameters were learning rates 0.001, regularization strengths 0.4, batch size 200, learning rate decay 0.95.
Best validation accuracy achieved during cross validation was 0.475.
Final test accuracy was 0.477.