해시 브라운(Hash Brown) to 비트코인(Bitcoin)

ephist·2023년 10월 29일

Summary

해시 브라운(Hash Brown)과 해시 테이블(Hash Table)

맥도날드에 '해시 브라운'이라는 감자로 만든 사이드 메뉴가 있음.

해시(Hash): 원래는 '잘게 썬 음식'을 가리키는 용어로, 컴퓨팅 영역에서는 데이터를 작은 조각으로 쪼개고, 이를 규칙에 따라 섞어 새로운 형태로 변환하는 과정을 뜻함.

해시 테이블(Hash Table): 키(Key)를 해시 함수(Hash Function)를 통해 해시값(Hash Value)으로 변환하고, 이를 인덱스(Index)로 사용해 값(Value)을 저장/검색하는 데이터 구조.

리스트(List)/사전(Dictionary)

Python의 리스트(List)와 사전(Dictionary)은 탐색 시간(searching time)에 차이가 있음.

List: 탐색 시간이 O(n) (선형 탐색, Linear Search).

Dictionary: 탐색 시간이 O(1) (상수 시간, Constant Search).

해시 함수(Hash Function)와 비트코인(Bitcoin)

해시 함수: 입력값을 받아 고정된 길이의 해시값을 출력하는 함수.

비트코인(Bitcoin): SHA-256 해시 함수를 사용하여 고유한 해시값 생성.

채굴(Mining): 새 비트코인 생성 및 거래 검증, 네트워크에 추가하는 과정. 작업 증명(Proof of Work)과 연관됨.

작업 증명: 채굴자가 특정 조건을 만족하는 해시값을 찾아야 함. 이를 위해 nonce를 사용하여 여러 해시 계산 시도.

Details

Hash Brown

맥도날드 맥모닝 사이드 메뉴에 해시 브라운 (Hash Brown) 이라는 게 있습니다. 짭짤하면서도 고소해서 좋아하는 메뉴 중 하나인데요, 여기서 Hash는 잘게 썬 음식물 또는 다양한 재료를 잘게 썰어 섞은 요리 를 가리키는 용어입니다.

Hash/Hash Table

컴퓨팅 분야에서 Hash는 데이터를 작은 조각으로 쪼개고 이를 특정 규칙에 따라 섞어서 완전히 새로운 형태로 변환한다 는 의미로 확장해서 사용됩니다. 아직 해시 브라운이 머릿속에 있다면 어렵지 않게 받아들일 수 있는 확장입니다.

Hash table은 hash를 활용하는 데이터 구조 중 하나로, 이 구조에서는 키 (key) 를 해시 함수(hash function) 를 통해 해시값(hash value) 로 변환하고, 이 해시값을 인덱스(index) 로 사용하여 값(value) 을 저장하거나 검색합니다. 참고로 hash value = index != value 이니 혼동하지 마시길 바랍니다.

List/Dictionary

Coding을 조금이라도 접해보신 분이라면 array 혹은 list 개념을 아실 것입니다. 둘 다 비슷한 개념이지므로 앞으로는 python에서 사용하는 list로 통칭하겠습니다.

List만 하더라도 데이터 구조를 다루는데 충분할 것 같지만 어느 순간 dictionary의 유용성을 깨닫기 시작합니다.

# List
fruits = ["사과", "바나나", "체리"]

# Dictionary
person = {
    "이름": "홍길동",
    "나이": 30,
    "도시": "서울"
}

이미 짐작하신 분들도 계시겠지만 python의 dictionary가 바로 hash table을 사용해 구현된 자료 구조입니다. 우리가 알고 있는 dictionary의 key, value 가 바로 위에서 얘기한 key, value 와 같습니다 (다시 한 번 말씀드리지만 hash value 가 아닙니다)

이 두 자료형에는 많은 차이점이 있지만 우선 searching time 관점에서 비교해 보도록 하겠습니다.

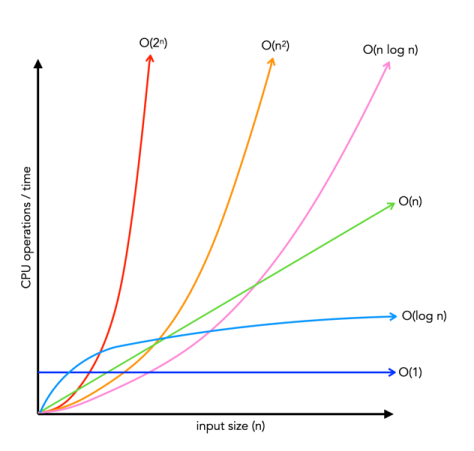
O(n) vs O(1)

굳이 Big O Notation 까지 알 필요는 없습니다만 그냥 넘어가면 섭섭하니깐 아주 가볍게 O(n) 과 O(1) 두 가지만 짚고 가죠.

O(n) 이라함은 작업을 수행하는데 걸리는 시간이 입력 데이터의 크기 (n) 에 비례한다 는 뜻이고, O(1) 이라함은 입력 데이터의 크기와 상관없이 항상 일정하다 는 것을 의미합니다. Linear search는 O(n), constant search는 O(1)에 해당합니다.

예를 들어 상자 안에 공이 하나 있다고 가정합시다. 이 공을 찾기 위해서 상자를 열어보는 작업은 상자 안의 공의 개수와 상관없이 (10개든, 100개든, 1000개든) 한 번만 열면 되니, 이것이 O(1)입니다. 반면, 공이 여러 개 있고 특정 숫자가 적힌 공을 찾아야 한다면, 최악의 경우 모든 공을 다 확인해봐야 합니다. 공이 100개 있으면 최대 100번, 1000개 있으면 최대 1000번 확인해야 하죠. 이런 경우가 O(n)입니다.

List 안에 특정 원소(element)가 있는지 확인하는 데 걸리는 시간은 O(n)인데 반해 hash table 에서 특정 키(key)가 있는지 확인하는 데 걸리는 시간은 O(1) 입니다 (엄밀히는 ~O(1), 즉, O(1)에 근접합니다). 즉, 데이터의 양이 많을 때 hash table이 훨씬 빨리 key (혹은 element) 에 접근할 수 있다는 뜻이죠. 아래는 list로 원래 표현했어야 했지만 hash table의 search time 장점을 활용하기 위해 (그다지 의미없는 value와 함께) dictionary로 만든 자료 구조입니다. (참고로 search 뿐만 아니라 add/remove 시에도 O(1) 입니다)

# List
fruits_list = ["사과", "바나나", "체리", "귤"]

# Dictionary
fruits_dict = {
    "사과": True,
    "바나나": True,
    "체리": True,
    "귤": True
}

여기서 이상한 점을 느끼셨다면 당신은 매우 이성적이고 비판적으로 글을 읽는 사람이란 것을 자부하셔도 좋습니다. 아마도 이런 질문이 떠올랐을 것입니다.

Hash table은 list와 같이 index와 value 쌍을 가지고 있는데 어떻게 list보다 빠를 수 있을까요?

이 magic을 가능하게 해 주는 것이 바로 해시 함수(hash function) 입니다.

Hash Function

Hash Function 은 어떤 입력값(데이터)을 받아, 고정된 길이의 문자열이나 숫자 등의 해시값(hash value) 을 출력하는 함수를 말합니다. Hash function은 사용자가 정의하기 나름이므로 어떤 것도 될 수 있습니다.

예를 들어 위의 fruits_dict 에서 hash function을 '글자의 개수' 라고 정했다고 해 봅시다. 그럼 각각의 hash value는 아래와 같이 되겠죠.

사과 -> Hash Function (글자의 게수) -> 2
바나나 -> Hash Function (글자의 개수) -> 3
체리 -> Hash Function (글자의 개수) -> 2
귤 -> Hash Function (글자의 개수) -> 1

이 경우 사과와 체리가 모두 2라는 hash value로 mapping 되므로 (이를 해시 충돌(hash collision)이라고 합니다) 이후에 이 둘을 구분하기 위해서는 다시 한 번 searching이 필요할 것입니다. 가장 쉽게는 다시 한 번 linear search를 해 주면 되겠죠 (이런 경우가 발생할 수 있기 때문에 hash table의 searching time이 O(1) 보다는 살짝 증가합니다). 하지만 이런 경우가 많아지면 hash table의 장점이 반감되므로 좀 더 복잡한 hash function을 만들어보죠. 이번엔 '자음과 모음 개수의 합' 이라고 정의해 보겠습니다.

사과 -> Hash Function (자음과 모음 개수의 합) -> 5
바나나 -> Hash Function (자음과 모음 개수의 합) -> 6
체리 -> Hash Function (자음과 모음 개수의 합) -> 4
귤 -> Hash Function (자음과 모음 개수의 합) -> 3

이번엔 모두 유일한 hash value가 나왔네요. 하지만 곧 다른 데이터가 들어온다면 처음과 비슷한 상황이 발생할 거란 걸 쉽게 알 수 있습니다.

다행히도 hash table을 사용하기만 하면 되는 (대다수의) 여러분은 더 이상 어떤 hash function을 사용해야하는지 고민할 필요가 없습니다. 이미 똑똑한(!) 수학자들이 가능하면 겹치지 않는 hash value를 만들어주는 많은 hash function들을 고안해냈고, 대부분의 프로그래밍 언어, 보안, 혹은 암호화폐(crypto currency) 영역에서 쓰이고 있습니다 (드디어 암호화폐가 등장했네요!)

마지막으로 해시 함수가 가지면 좋은 특징들은 다음과 같습니다. 이런 특징들이 있으면 왜 좋을까 에 대해 한 번 생각해 보시기 바랍니다.

결정성(Deterministic): 동일한 입력값에 대해 해시 함수는 항상 같은 해시값을 반환해야 합니다.

고정된 길이의 출력: 입력값의 길이에 관계없이 해시 함수는 고정된 길이의 해시값을 생성합니다. 예를 들어, 매우 긴 텍스트든 단 한 글자든, 결과 해시값은 동일한 길이를 가집니다.

빠른 계산 속도: 해시 함수는 입력값에 대해 해시값을 매우 빠르게 계산할 수 있어야 합니다.

해시 충돌의 최소화: 서로 다른 두 개의 입력값이 동일한 해시값을 가지는 경우를 '해시 충돌(hash collision)'이라고 하는데, 좋은 해시 함수는 이러한 해시 충돌의 발생 가능성을 최소화합니다.

원본 데이터의 추론 어려움: 해시값만 보고는 원본 입력값을 추론하기 어렵도록 해야 합니다. 이는 특히 암호학적 해시 함수에서 중요한 요소입니다.

Bitcoin (Finally!)

비트코인 백서 (Bitcoin Whitepaper) 의 초록에 다음과 같은 문장이 있습니다.

The network timestamps transactions by hashing them into an ongoing chain of hash-based proof-of-work, forming a record that cannot be changed without redoing the proof-of-work.

이제는 우리에게 익숙한(?) hash라는 단어가 나왔네요. 이는 Bitcoin 뿐만 아니라 많은 crypto currency에서 매우 중요한 동작 원리 중 하나입니다. Bitcoin에서는 주로 SHA-256 (Secure Hash Algorithm 256-bit) hash function을 사용합니다. 이 함수는 입력 데이터에 대해 256비트 길이의 고유한 hash value를 생성합니다.

Mining

Bitcoin 채굴(Mining) 은 새로운 Bitcoin을 생성하고, 동시에 거래를 검증하고 네트워크에 추가하는 과정입니다. 이 과정에서 중요한 역할을 하는 것이 바로 작업 증명(Proof of Work) 입니다.

채굴자들은 특정 조건을 만족하는 hash value를 찾아야 합니다. 예를 들어, Bitcoin 네트워크는 hash value의 앞부분이 특정 수의 연속된 0으로 시작하도록 요구할 수 있습니다. 이 조건을 만족하는 hash value를 찾기 위해 채굴자들은 거래 데이터에 nonce 라는 숫자를 추가하여 무수히 많은 hash 계산을 시도합니다. 이 nonce가 앞서 우리가 살펴보았던 key 에 해당합니다. 즉, 적절한 nonce 값을 찾아 조건에 부합하는 hash value를 생성하는 것이 채굴의 목표 입니다. 이는 매우 복잡하고 연산 집약적인 과정이기 때문에, 이를 해내는 채굴자에게는 새로 생성된 Bitcoin과 수수료가 보상으로 주어집니다.

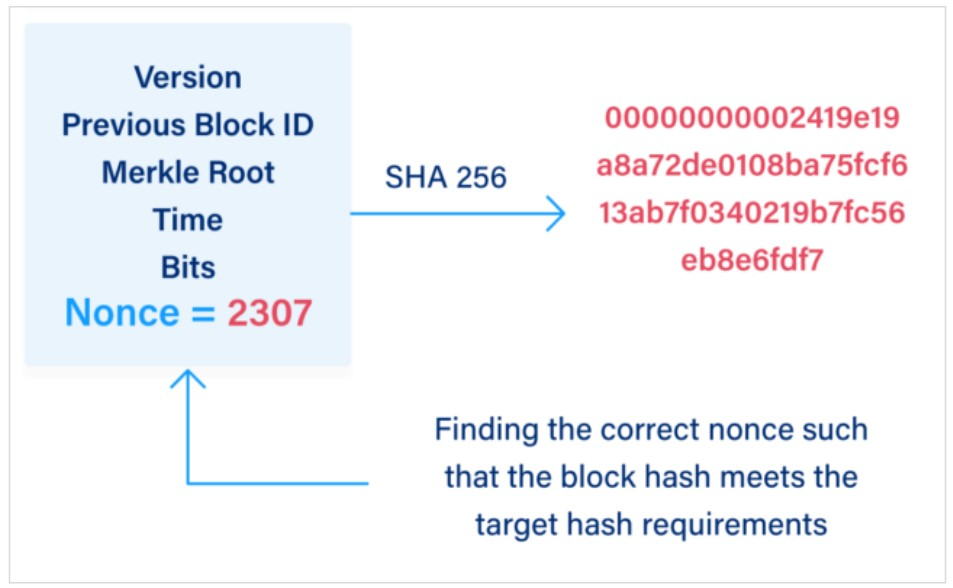
Nonce는 (이론상) hash value로부터 곧바로 계산해낼 수 없습니다. 따라서 mining이라는 과정은 사실상 nonce를 찾기 위한 노가다 라고 정의할 수 있겠죠. 맞는 답이 나올 때까지 무식하게 방정식에 x값을 대입시켜보는 과정이라고도 볼 수 있습니다.

Epilogue: GPU/NVIDIA/Quantum Computing

CPU는 똑똑한 녀석, CPU보단 덜 똑똑하지만 (비교적 쉬운) 많은 일을 잘하는 게 GPU다보니 mining에는 GPU가 적합할 수밖에 없었고, 암호화폐 boom 때 NVIDIA graphic card가 불티나게 팔릴 수밖에 없었죠.

Quantum computing은 전통적인 computing보다 훨씬 더 많은 정보를 동시에 처리할 수 있기 때문에 만약 현실화된다면 mining 시간이 획기적으로 줄어들게 될 것입니다. 그 때가 되면 Bitcoin의 반감기는 급속도로 빨라지고 (현재는 2140년 경으로 예상하는) 2100만개의 모든 Bitcoin 채굴이 금방 끝날 것이라고 보는 시각이 많습니다.