▪️ 의문점: 2011년도의 해상도 최대가 270p인 강의가 지금도 남아 있는 비결은 무엇일까? 그리고 6.006/6.046?의 의미는 무얼까?🤔
▪️ 인상 깊은 점: 강의 자료가 잘 정리되어 있음. 칠판을 (6 + @)개 쓰는 클래스 🤣
About
-
강의 계획서
https://courses.csail.mit.edu/6.006/spring11/notes.shtml -
강연자(Erik Demaine) 홈페이지
https://erikdemaine.org/
1. Introduction
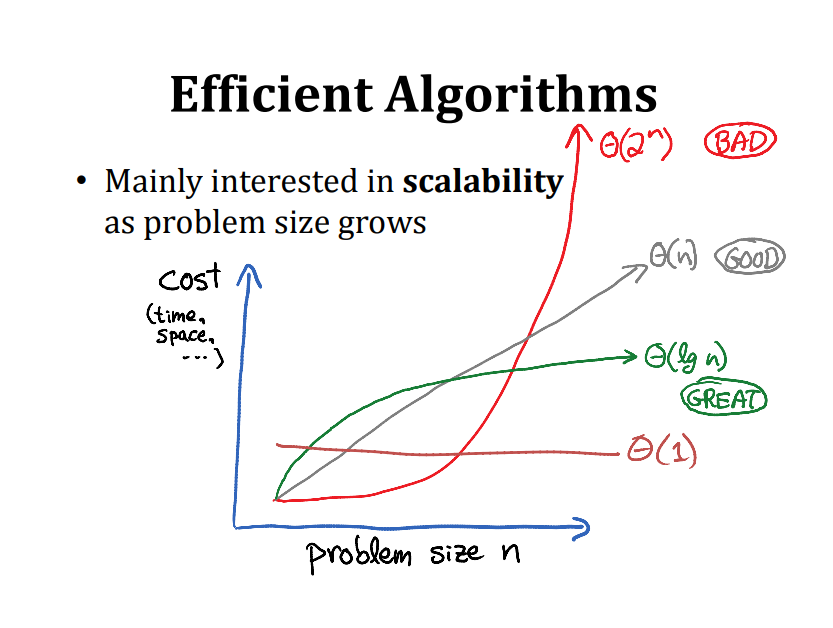
- 큰 입력을 받는 문제를 처리하기 위한 효율적인 방법에 관한 수업
- 확장성: 입력이 커짐에 따라 알고리즘이 어떻게 진행될 지 추적할 수 있어야 한다.
- 알고리즘 설계는 일부, 알고리즘 분석
- 후속 과목 6.046 : 알고리즘의 설계
개요
- 알고리즘 사고 (Algorithmic thinking)
- 정렬과 트리(Sorting & tree)
- 해싱(Hashing)
- 수 (Number: RSA)
- 그래프 - 루빅 큐브 (Graphs- rubiks'cube)
- 최단 경로(shortest paths: Caltech -> MIT)
- 이미지 압축(Dynimic programming: Image compression)
- Advanced topics
🔷극대값 찾기
문제: 극댓값이 존재할 경우 그 값을 찾아라.
cf. 질문에 대한 답을 찾을 수 없거나 모든 요구 조건을 만족하지 못 했을 때, 포기하고 이렇게 얘기한다.
오랫동안 열심히 찾아봤습니다. 열심히 노력한 흔적이 여기 있는데, 그럼에도 불구하고 찾지 못했습니다.😀
- 시작점 설계 왼쪽에서 시작해서 가로지르기
- 최악의 경우 Θ(n) : 모두 확인해야 한다.
- 이 알고리즘의 점근적 복잡도(Asysmptotic Complexity)는 선형적..?
- 더 효율적으로
- 루빅큐브 방석을 받은 Chase의 알고리즘
- 재귀적(recursive) 알고리즘
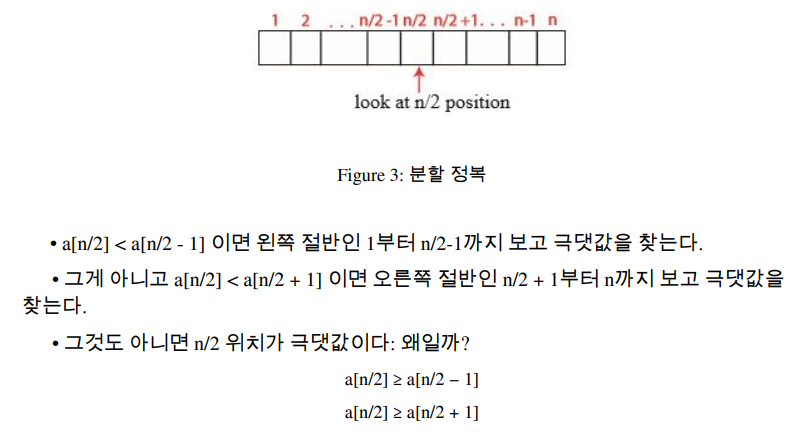
- 알고리즘 실행 시간에 관한 식:
T(n)의 점화식 = T(n/2) + Θ(1) = Θ(1) + ... + Θ(1) (cf. T(1) = Θ(1))
-> times = Θ
- 2차원
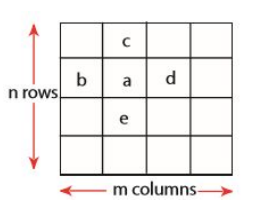
- a b, a c, a d, a e라면, a가 극댓값
- 탐욕 상승 알고리즘(Greedy Ascent algorithm) :
Θ(nm) 복잡도, m = n이면 Θ(n2) - 시도 1
- 중앙 열j = m/2를 선택
- (i,j)에서 1차원 극댓값 찾기
- (i,j)를 시작 지점으로 하여 i행에서 1차원 극댓값을 찾는다.
- but, 효율적이나 틀렸다.
(복잡도 지만, 극댓값이 i행에 존재하지 않을 수도 있다.)
- 시도 2
- 중앙 열 j = m/2 선택
- (i,j)에서 j열의 최댓값을 찾는다.
- (i, j-1),(i,j),(i,j+1)를 비교한다.
- (i, j-1)>(i,j)이면 왼쪽 열을 선택
- 오른쪽도 똑같이 진행
- if, 두 조건 모두 만족하지 않으면 (i,j)가 2차원 극댓값
- 열 개수가 절반으로 줄어든 새로운 문제를 푼다.
- 열이 1개 남으면, 최댓값을 찾았다!
- 복잡도: n개의 행과 m개의 열이 있는 문제를 해결하기 위한 일의 양을 T(n,m)
T(n, m) = T(n, m/2) + Θ(n)
= Θ(n) + Θ(n) + ... + Θ(n) () = Θ(n)
if, m = n이면, Θ(n)
🔷 계산 모델
알고리즘이란?
-
문제를 푸는 계산, 계산 과정을 정의하는 방법
-
컴퓨터 프로그램에 대응하는 수학적 표현
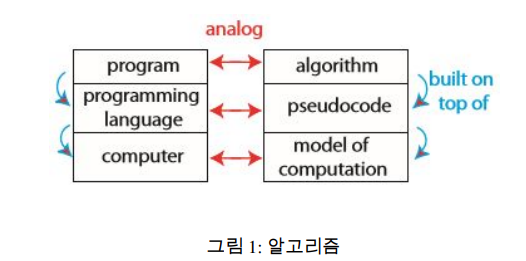
계산모델
- 컴퓨터가 상수의 시간 동안 할 수 있는 것이 무엇인지 알려준다.
- 알고리즘이 할 수 있는 연산과 그 연산의 비용/시간을 결정.
- 알고리즘의 총 비용 = 각각의 연산 비용의 총합(실행 시간)
<이론적 모델>
- 임의 접근 머신(Random Access Machine=RAM)
- 임의 접근 기억 장치(Random Access Memory)
- 거대한 배열(0~8/16GB)
- 워드(Word)
- w
- 포인트 머신(Point Machine)
- 동적으로 할당된 객체(namedtuple)
- 하나의 객체는 일정한 개수의 필드를 가진다.
- 필드는 워드(정수, 입력 객체, 계산 대상, 카운터 등을 저장하는 것) 또는 포인터(다른 객체를 가리키거나, null)
문서 거리 문제 d(D, D 계산
- D, D 이 유사한가?
- 공통으로 갖는 단어가 많으면 유사하다고 할 수 있음 - 단어: 영어와 숫자로 이루어진 문자열
- 문서: 단어들의 나열, 하나의 벡터
- 문서 거리: 두 벡터의 내적, 두 벡터 사이의 각도(0도에 가까우면 유사도가 높고, 90도라면 공통 단어가 없다.)

문서 거리 알고리즘
- 각 문서를 단어들로 쪼갠다.
- 단어 빈도를 센다(문서 벡터)
- 내적을 계산한다.

