🔷 정렬 & 트리
키워드
- 삽입 정렬
- 합병 정렬
- 재귀 풀이
삽입 정렬과 합병 정렬
1. 왜 정렬을 해야 할까?
= 여러 종류의 복잡한 프로그램에서 정렬은 서브루틴이다.
-
데이터 압축: 여러 항목으로 구성되어 있는데, 정렬을 하면, 중복된 아이템들을 찾을 수 있다.
-
컴퓨터 그래픽: 장면을 렌더링할 때, 해당 장면에 많은 층들이 존재한다. 대부분 렌더링은 앞에서 뒤로 진행(이게 효율적). 단, 투명도가 걱정된다면 뒤에서 앞으로 렌더링...(?)
-
입력 값의 종류나 문제의 종류의 따라 가장 빠른 알고리즘은 달라진다.
2. 삽입 정렬(Insertion Sort)
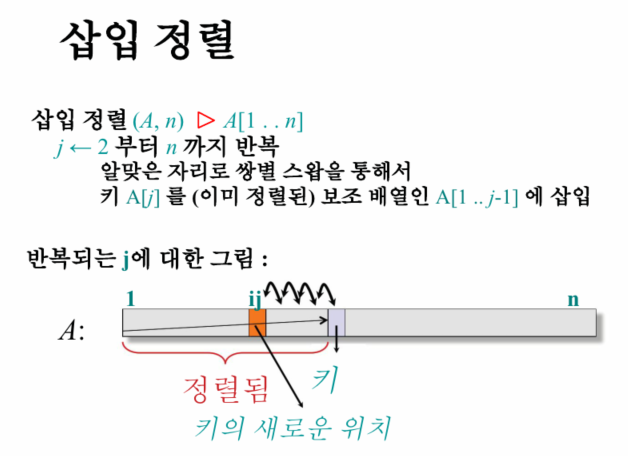
- 쌍별 스왑(pairwise swaps)을 통해 원래 A[i]에 있던 숫자를 알맞은 자리에 보냄. -> 두 수의 자리 바꿈이라는 의미다;

- 비교가 일반적으로 swap보다 비용이 많이 든다.
- pairwise -> binary search로 바꾸면, 복잡도를 개선할 수 있다.
3. 이진 탐색(binary search)
- 이미 정렬된 부분에서 탐색

4. 합병 정렬 (Merge Sort)
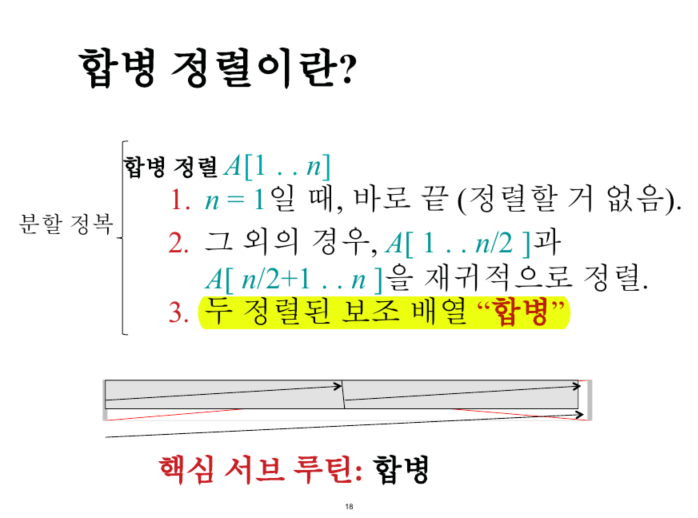
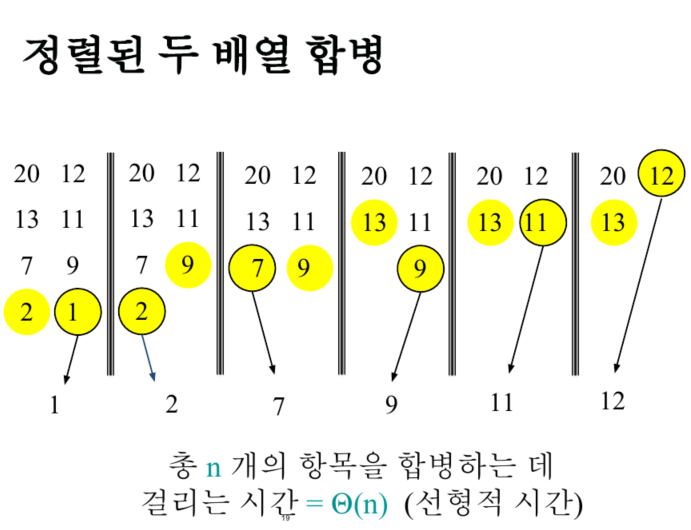
-
복잡도는 Θ(n) : 그림으로 증명.....⬇️
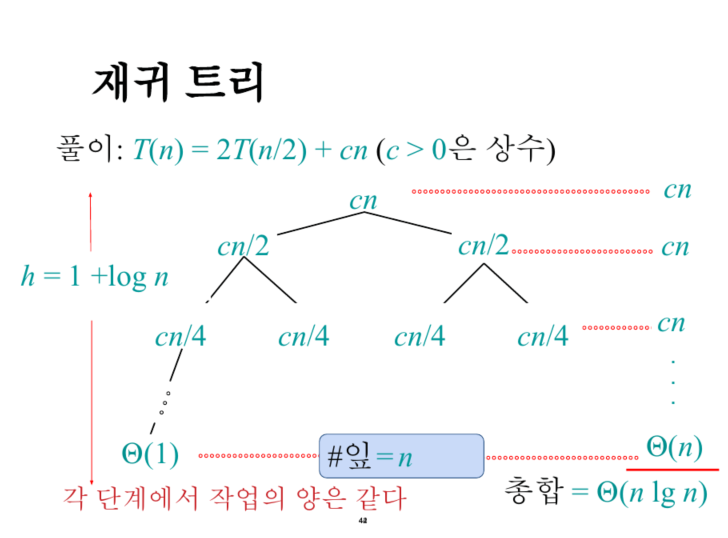
-
합병 정렬과 비교해서 삽입 정렬의 장점은?
삽입 정렬은 제자리 정렬이어서 추가 공간이 필요 없다. 즉, 보조 공간이 Θ(1)(swap 할 때, 사용되는 임시 변수. 거기에 덮어쓰는 것을 반복). 합병 정렬은 L L'이므로 Θ(n) 보조 공간이 따로 필요하다. -
제자리 합병 정렬도 있는데,
- 성능적으로 약간 비실용적임. 실행시간이 긺.
🔷 힙 & 힙 정렬
키워드
- 우선순위 큐
- 힙
- 힙 정렬
우선순의 큐(Priority Queue)
-
요소들 집합 S를 구현하는 자료구조
-
각 요소들은 키와 관련이 있고, 다음 작업들을 지원한다.
-
추상 자료형(abstract data type, ADT)의 명세(Specification). ADT란, 컴퓨터 과학에서 자료들과 그 자료들에 대한 연산들을 명기한 것이다.
- insert(S, x): 요소 x를 집합 S에 삽입
- max(S): 최대 키인 S의 요소를 반환
- extract_max(S): 최대 키인 S의 요소를 반환하고 집합 S에서 제거
- increase_key(S,x,k): 요소 x의 키를 새로운 값 k로 증가시킴
(k가 현재 값만큼 크다고 가정)
🔹 이번 강의에서는, 힙의 특성을 변하지 않게 하는 불변성에 대해 살펴볼 예정.
힙
- 우선 순의 큐의 구현
- 완전 이진 트리로 시각화된 배열
- 최대 힙 특성: 노드의 키가 자식 값들의 키보다 크다.(최소 힙도 마찬가지)
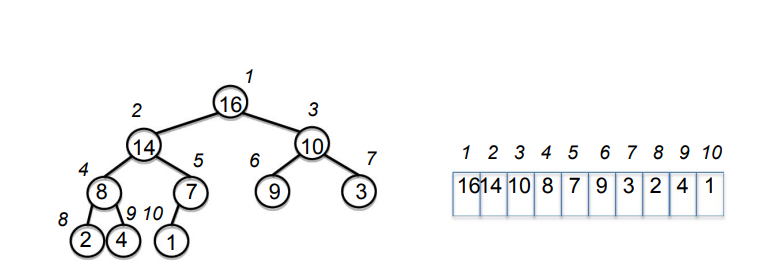

- 우선 순위 큐에서 할 수 있는 가장 간단한 작업: 우선순위 큐 생성하기, extract_max() 반복적으로 사용하기
Max_heapify
- method : 최대-힙 특성의 대표 불변량을 유지해 줌
- left(i)와 right(i) 서브 트리들이 최대-힙이라고 가정
- 만약 요소 A[i]가 최대-힙 특성을 위반한다면, 요소
트리A[i]를아래로 흘러 내려가도록 하면서 위반을 수정한다. 서브 트리들은 최대-힙으로 만든다.
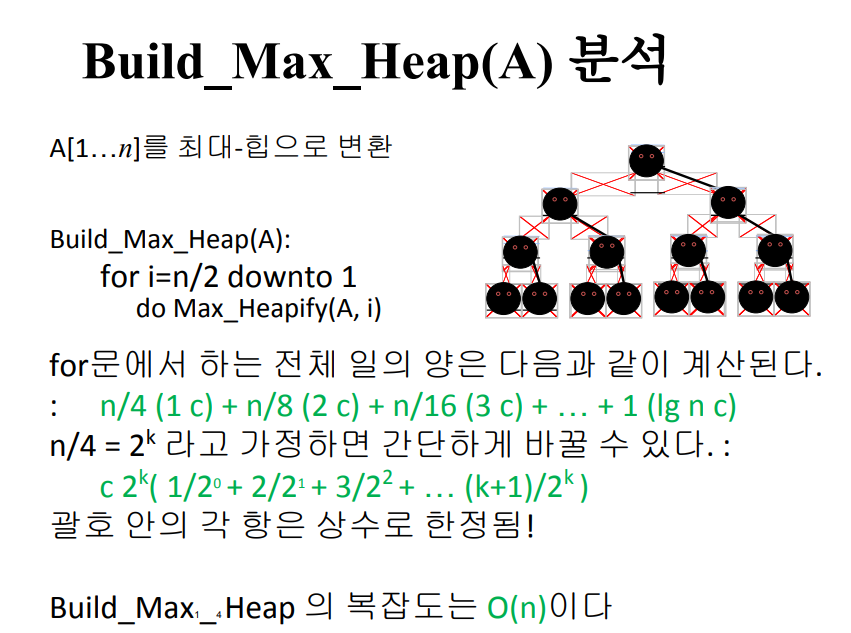
힙 정렬
정렬 전략:
1. 정렬된 배열에서 최대-힙을 만든다.
2. 최대 요소 A[1] 을 찾는다.
3. 요소 A[n]와 A[1]을 스왑한다. : 이제 최대 요소는 배열의 끝에 위치
4. 힙에서 노드 n 을 제거한다. (힙 크기 변수를 줄이는 방법을 통해)
5. 새로운 루트는 아마 최대-힙 특성을 위반할 것이다. 하지만, 그 자식 값들이 최대 힙이다. max_heapify로 해결한다.
6. 힙이 비어있지 않다면 2단계로 돌아간다.
실행시간: n번 반복 후 힙이 비게 된다. 각 반복은 swap과 max_heapify 작업을 포함. 따라서, O(log) 시간이 걸린다.
🔷 일정 예약과 이진 탐색 트리
키워드
- 활주로 예약 시스템: 정의, 이진트리로 해결하는 방법
- 이진 탐색 트리: 계산 과정
🤔 이번 강의부터 강의 자료가 조금 달라졌는데, 기존 강의자료보다도 더 잘 정리되어서 놀람. 너무 잘 되어있어서 내가 정리할 게 없을 정도...ㅎㅎ
1. 활주로 예약 시스템

더 나은 방법?
• 정렬된 리스트: 추가 및 정렬에는 Θ(nlogn) 시간이 소요된다. 추가와 정렬 과정을 하지 않고 새로운 시간/비행기를 삽입할 수 있다. 그러나 삽입에는 Θ(n)만큼 시간이 소요된다. 삽입 위치가 파악되기만 하면 k분 떨어져 있는지 확인하는 작업은 O(1) 안에 가능하다.
• 정렬된 배열: 이진 탐색을 이용하여 O(lg n) 시간 안에 삽입하려는 위치를 찾을 수 있다. 이진 탐색을 이용하여 R[i] ≥ t 를 만족하는 최소의 i 값을 찾을 수 있다. (예를 들면, 다음으로 큰 요소) 그 다음 t에 대해 R[i] 와 R[i − 1] 비교한다. 실제 삽입 과정에는 Θ(n) 시간이 소요되는 자리 이동 필요
• 정렬되지 않은 리스트/배열: k분 떨어져 있는지 확인하는 데에 O(n)만큼
시간이 소요된다.
• 최소-힙: O(lg n) 시간 안에 삽입 가능하다. 그러나 k분 떨어져 있는지 확인하는 데에는 O(n) 시간만큼 소요된다.
• 딕셔너리 또는 파이썬 Set: 삽입은 O(1)만큼 시간이 소요된다. k분 떨어져 있는지 확인하는 데에는 Ω(n)만큼 시간이 소요된다.
cf. 배열은 자리이동 시 좋지 않다. (삽입 후 기존 원소가 다 움직여야 함)
so.. 정렬된 리스트에 빠르게 삽입하려면 어떻게 해야 하는가?
2. 이진 탐색 트리(BTS: Binary Search Trees)
🔹 특성
이진 트리의 각 노드 x에는 키인 key(x)가 있다. 루트가 아닌 다른 노드는 부모인 p(x)가 있다. 노드에는 왼쪽 자식인 left(x) 와 오른쪽 자식인 right(x)이 있다. 이것들은 힙과는 달리 포인터이다.
불변성 : 모든 노드 x와 x의 왼쪽 하위 트리에 있는 모든 노드 y에 대해서 key(y) ≤ key(x)이다. 또한 x의 오른쪽 하위 트리에 있는 모든 노드 y에 대해 key(y) ≥ key(x)이다.
🔹 삽입
삽입: insert(val)
그림 2와 같이, 알맞은 위치를 찾을 때까지 왼쪽 및 오른쪽 포인터를 따라 내려간다. 삽입을 하는 도중에 활주로 예약 시스템에서 “k=3 내”에 다른 예약이 있는지 확인이 가능하다. 루트에서부터 보았을 때, 삽입을 원하는 값의 k=3 이내에 있는 다른 요소를 발견하게 되면, 과정을 중단하고 삽입하지 않는다.
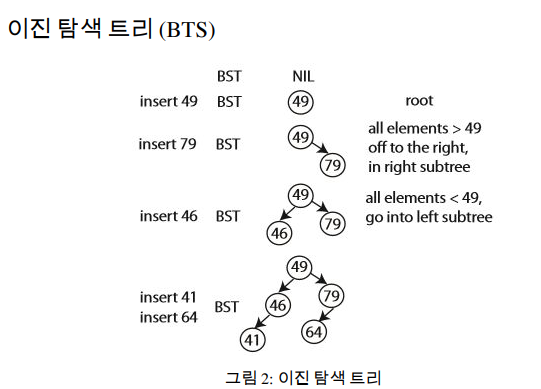
- 무수한 포인터들이 트리 구조에 추가되어 있는 걸 제외한다면 정렬된 배열과 같다. 정렬된 리스트와 정렬된 배열의 중간.
- h: 트리의 높이라면, 확인을 하든 안하든 O(h)의 시간이 든다. -> 이게 이진 탐색 트리의 장점.
🔹새로운 요구 조건
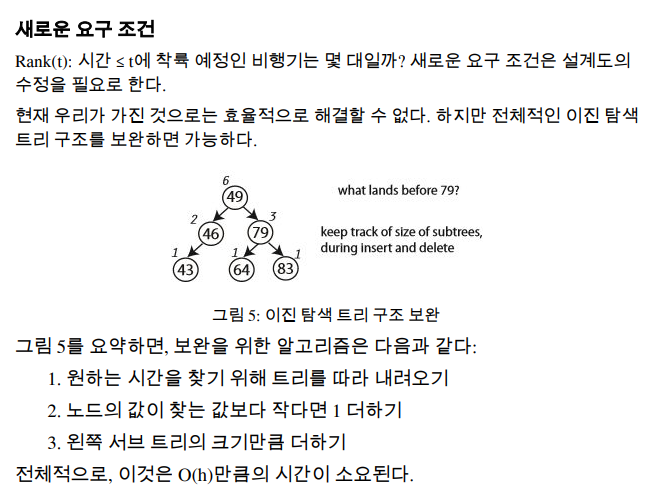
균형 이진 탐색 트리의 개념이 필요하다..?
균형 이진 탐색 트리(Balanced BSTs)
키워드
- 균형을 이루는 것의 중요성
- AVL 트리
- 정의와 균형
- 회전
- 삽입
- 다른 균형 트리들
- 일반적인 데이터 구조들
- 하한
1. 균형을 이루는 것의 중요성
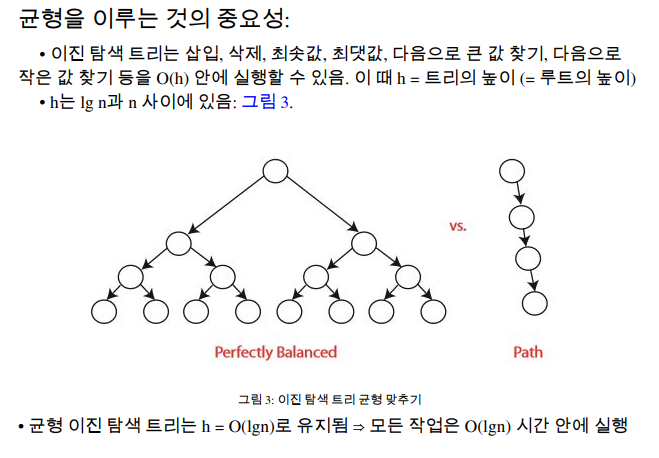
- 루트부터 잎까지의 가장 긴 경로는 이진 탐색 트리의 높이와 같다.
🔹 오늘의 목표는 트리가 항상 균형 잡히도록 유지하는 것.
2. AVL 트리
- 노드의 높이(height of node): 그 노드에서부터 단말 노드(?leaf node)까지 가장 긴 경로.
- 노드의 높이 계산: 자식의 높이의 최대 +1, 왼쪽 자식 높이와 오른쪽 자식 높이 중 큰 값에 +1

