WHY MACHINES LEARN(기계는 왜 학습하는가)

부제: The elegant math behind modern AI

Anil Ananthaswamy

(사진 출처: linkedin)

저자 홈페이지: https://anilananthaswamy.com/

느껴진다. 유쾌한 수학 덕후의 향기가! 😃

원문

링크드인에 저자 분이 직접 책을 소개하는 글이 있어서 그대로 가져왔다.

What's So Elegant About the Math of Machine Learning? I have often been asked this question, given it's the sub-title of WHY MACHINES LEARN.

If you have been studying machine learning for a long time, the elegance might not be obvious. But if you came to ML like I did--decades after having studied the relevant math for my undergrad and graduate EE degrees, and decades after having done regular software engineering--then machine learning hits you like a ton of bricks.

Who would have thought that basic ideas like vectors, matrices, matrix-vector multiplication, differential calculus, gradient descent, elementary probability and statistics -- all of which you learn in high school or at least during the first years of undergrad in STEM -- would form the basis of the extraordinary revolution that's underfoot?

But that's just wonder. What about elegance? Well, that's really a subjective perspective. Again, many might disagree. But here's a sampling of the kinds of things I found beautiful:

The Perceptron Convergence Proof: It's just linear algebra, but the proof of why the perceptron algorithm will linearly separate two clusters of data in finite time, if such a divide exists, is a thing of beauty.

Support Vector Machines and Kernel Methods: These algorithms have been somewhat forgotten, given the success of deep neural networks, but when you encounter the formulation of SVMs, and the use of kernel methods to project data into higher dimensions -- it's such a counter-intuitive thing to do--you can't but be amazed. I was!

Hopfield Networks Convergence Proof: Again, just linear algebra shows you something very powerful--that these networks will settle into an energy minimum when perturbed and retrieve what amounts to a stored memory! Think about that. I can't help wonder whether our brains are doing something similar. John Hopfield--who won the @NobelPrize in Physics in 2024 for this work--certainly did.

The Backpropagation Algorithm: This might be a contentious candidate; some don't think it's elegant. But I find backprop powerful, and consequently elegant. Something that can be used to train a tiny, tiny neural network with just one hidden neuron can also be used to train the giant Large Language Models of today. The elegance is in its power. It's almost certainly not what our brains are doing, but still!

All of this and more, of course, is detailed in WHY MACHINES LEARN.

머신러닝의 수학이 왜 그렇게 우아할까?
이 질문을 자주 받습니다. 제 책 WHY MACHINES LEARN의 부제가 바로 그것이기 때문이죠.

오랫동안 머신러닝을 공부해 온 사람들에게는 그 우아함이 당연하게 느껴질 수도 있습니다. 하지만 저처럼 학부와 대학원에서 전자공학(EE)을 전공하고, 이후 오랜 시간 일반적인 소프트웨어 엔지니어링을 하다가 머신러닝을 접한 경우, 그 충격은 이루 말할 수 없습니다.

누가 감히 예측했을까요? 벡터, 행렬, 행렬-벡터 곱셈, 미적분학, 경사 하강법, 확률과 통계 같은 기초적인 개념들이 지금 우리가 목격하는 엄청난 혁명의 토대가 될 줄이야!

하지만 그것은 단순한 경이로움입니다. 그렇다면 우아함은 무엇일까요? 사실, 이는 주관적인 문제입니다. 많은 이들이 동의하지 않을 수도 있겠죠. 하지만 제가 아름답다고 느낀 몇 가지를 소개하겠습니다.

퍼셉트론 수렴 증명
이것은 단순한 선형대수로 이루어진 증명입니다. 하지만 퍼셉트론 알고리즘이 두 개의 데이터를 유한한 시간 안에 선형적으로 분리할 수 있다는 사실을 증명하는 과정은 정말 아름답습니다.

서포트 벡터 머신(SVM)과 커널 방법
최근에는 딥러닝의 성공으로 인해 다소 잊혀진 알고리즘이지만, SVM의 수학적 공식화와 커널 방법을 이용해 데이터를 고차원으로 투영하는 개념을 접하면 감탄할 수밖에 없습니다. 처음 보면 정말 직관에 반하는 개념이지만, 그 작동 원리를 이해하면 놀라움을 금할 수 없습니다. 저도 그랬습니다!

홉필드 네트워크의 수렴 증명
역시 선형대수를 이용한 증명이지만, 이를 통해 네트워크가 외부의 자극을 받더라도 에너지 최소점으로 수렴하며 마치 기억을 복원하는 것처럼 동작한다는 사실을 알게 됩니다. 이것을 생각해보면 정말 신기합니다. 어쩌면 우리의 뇌도 이와 비슷한 방식을 사용하는 것이 아닐까요? 2024년 노벨 물리학상을 수상한 존 홉필드(John Hopfield)도 같은 생각을 했겠죠.

역전파(Backpropagation) 알고리즘
이 항목은 다소 논란이 있을 수 있습니다. 일부는 역전파가 우아하지 않다고 생각하기도 합니다. 하지만 저는 역전파가 강력하기 때문에 오히려 우아하다고 봅니다. 단 하나의 은닉 뉴런(hidden neuron)을 가진 작은 신경망을 학습시키는 데 사용할 수 있는 알고리즘이, 오늘날 거대한 대형 언어 모델(LLM)도 학습시킬 수 있다니! 그 자체로 우아함이 아닐까요? 물론 우리의 뇌는 역전파와는 다른 방식으로 학습할 가능성이 크지만, 그럼에도 불구하고 말이죠.

이 외에도 많은 내용이 WHY MACHINES LEARN에 담겨 있습니다.

about

여기에도 Erdos가!

몬티 홀 딜레마

미국의 TV 게임 쇼 <Let's Make a Deal>에서 유래한 퍼즐

세 개의 문 중에 하나를 선택하여 문 뒤에 있는 선물을 가질 수 있는 게임쇼에 참가했다. 한 문 뒤에는 자동차가 있고, 나머지 두 문 뒤에는 염소가 있다. 이때 어떤 사람이 예를 들어 1번 문을 선택했을 때, 게임쇼 진행자는 3번 문을 열어 문뒤에 염소가 있음을 보여주면서 1번 대신 2번을 선택하겠냐고 물었다. 참가자가 자동차를 가지려할 때 원래 선택했던 번호를 바꾸는 것이 유리할까?

➡️ Yes, 문을 바꾸는 게 유리하다.

💡 풀이

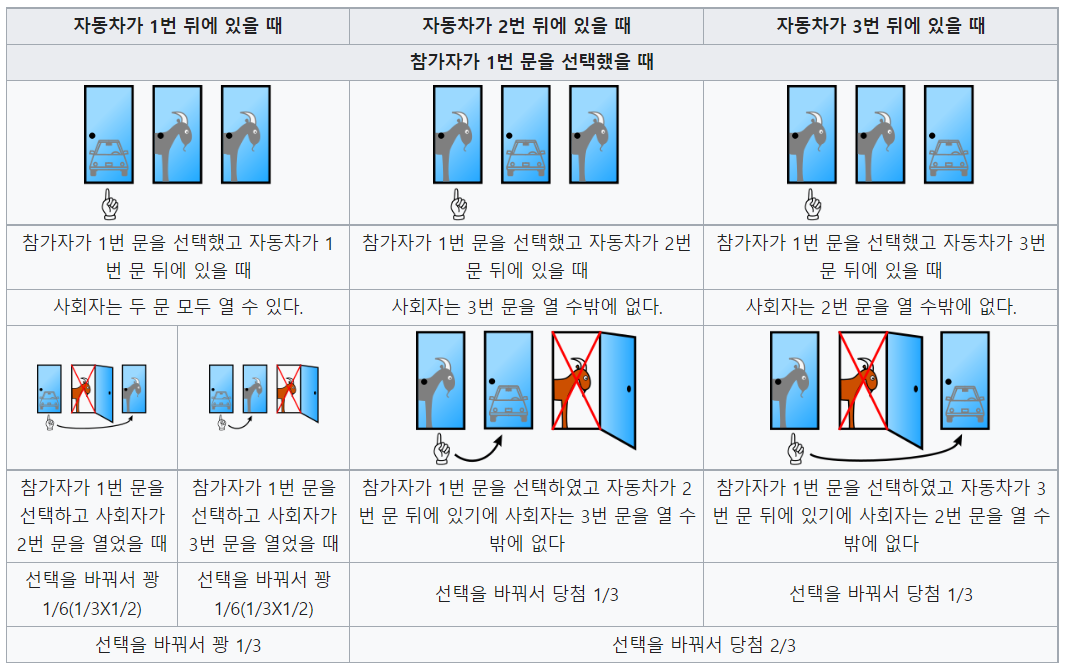
(출처: 위키백과 https://ko.wikipedia.org/wiki/%EB%AA%AC%ED%8B%B0_%ED%99%80_%EB%AC%B8%EC%A0%9C)

감상평

제 AI의 지식은요..

• 6개월 공부 한 적은 있음
• ML은 그럭저럭 즐겁게 했는데, Deep Learning은 흐린 눈으로 공부했다.
  개념, 역사적인 키워드만 인지한 정도다.
  딥러닝에 왜 질색하게(!) 되었는가 고심해보면, 구체적인 근거 없이 추상적인 결과가 너무 이상하게 느껴졌다.

이 책 덕분에..

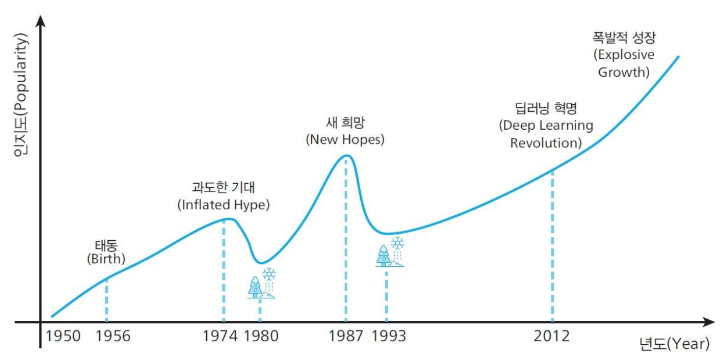
• 이 단순한 그래프에 실제했고 현재도 존재하는 수많은 사람들과 이론들을 차근차근 설명해 준다. 그래서인지 질색하던 딥러닝도 조금 재미있게 느껴졌다.

• 오랜만에 PCA를 찾아 보았는데, 그림이 너무 환상적이라 😃.
  
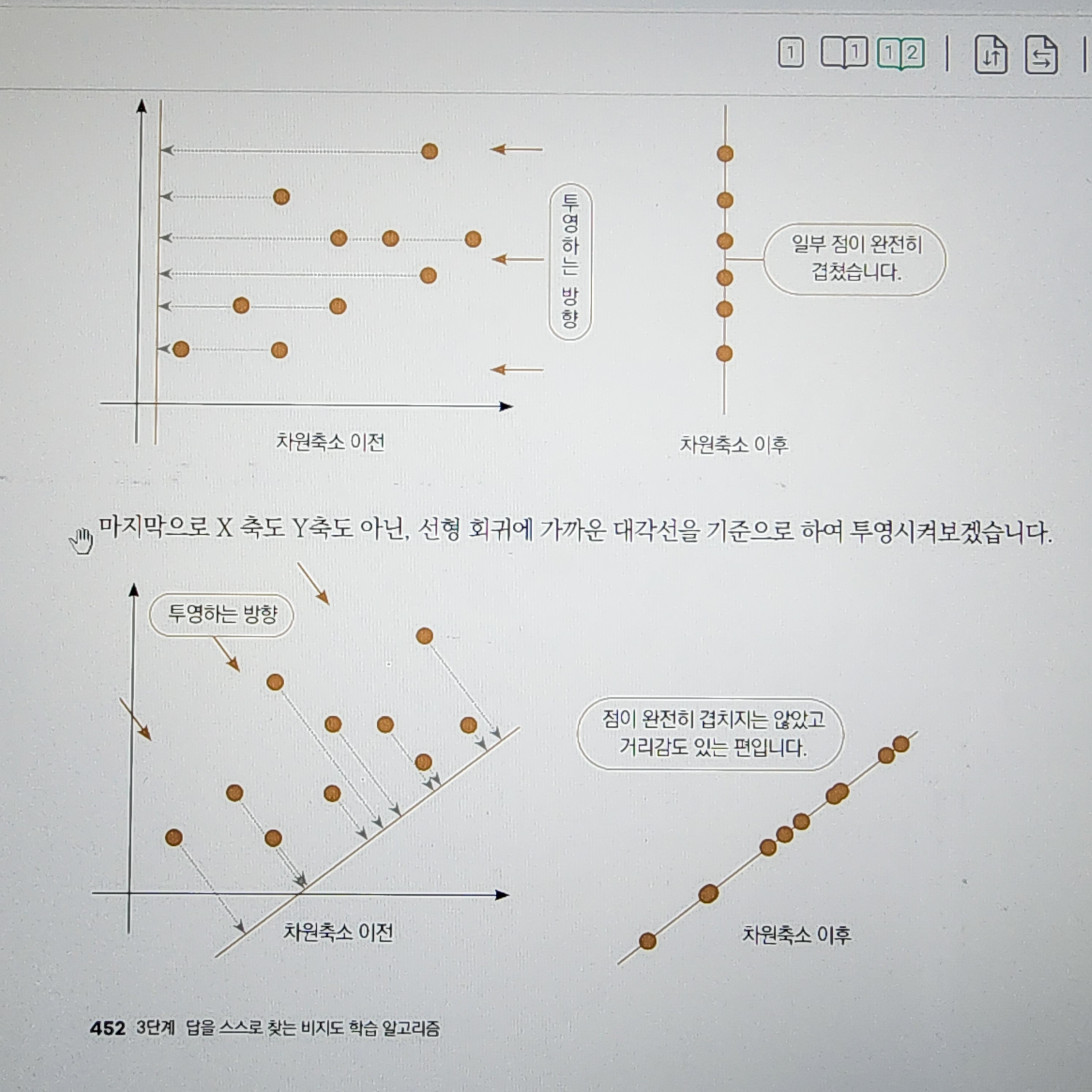
  (출처: 데싸노트의 실전에서 통하는 머신러닝)

  주성분 분석 (Principal Component Analysis, PCA): 데이터의 차원을 줄이고, 데이터의 주요 특징을 유지하는 통계적 기법

• AI에 들어있는 우아한 수학에 대해 확실히 알게 되었다.
  대체 어떤 수학이 들어있는 건데? 에 대답을 그럭저럭 할 수 있을 것 같다.

참고사항

• ML과 AI의 기본 지식이 있는 게 좋을 것 같음.
  최소 머신러닝 기본서 1권, 딥러닝 기본서 1권
• 수학 공식이 무척 많다.
  모든 것을 다 알 필요는 x, 중요한 부분만 기록/이해하려는 노력 정도면!