다이나믹 프로그래밍(DP) / 평범한 배낭(boj 12865)

정의

다이나믹 프로그래밍(동적 계획법)은 하나의 큰 문제를 여러 개의 작은 문제로 나누어 결과를 저장하고 다시 큰 문제를 해결하는 방식의 알고리즘이다. 쉽게 말하자면 이전의 저장한 값으로 다음 값을 얻어가며 문제를 풀어가는 방식이다.

재귀와의 차이점

큰 문제를 작은 문제로 나누어 해결한다는 과정에서 재귀와 비슷하게 들릴 수도 있지만 재귀는 자기 자신을 재참조 함으로써 하위 문제를 찾아가며 문제를 해결 하는 Top-Down 방식이지만 DP는 이미 연산된 작은 값들을 활용하여 큰 문제를 해결하는 Bottom-Up 방식의 알고리즘이다.

동적 계획법의 목적

동적계획법은 이전의 구한 문제의 값을 저장하기 때문에 중복되는 연산을 하지 않도록 해준다. DP의 가장 유명한 예시인 피보나치 문제를 통해 DP의 원리를 알아보자!

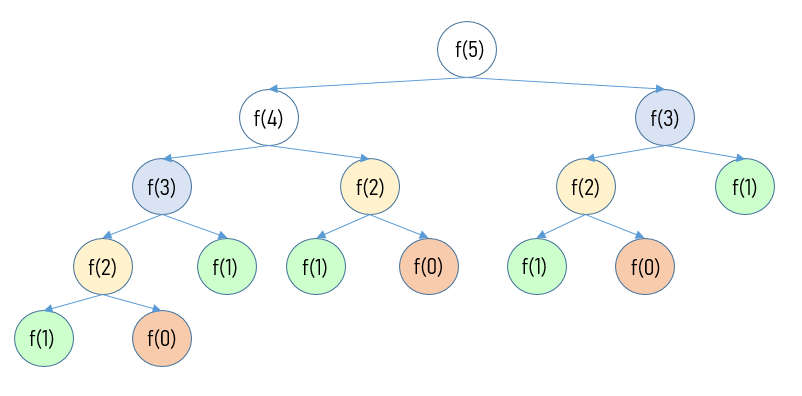
재귀로 구현한다면 return f(n) = f(n-1) + f(n-2)의 방식으로 문제를 풀 수 있을 것이다. 이때 연산 과정을 트리로 그려본다면 아래와 같을 것이다. 이렇듯 같은 연산이 반복해서 호출 하는 것을 볼 수 있다.

반면에 동적 계획법을 활용 한다면 dp[n] = dp[n-1] + dp[n-2]의 방식으로 문제를 해결 할 수 있다. dp[0]과 dp[1]의 값만 미리 넣어준다면 반복문을 통해 그 다음값을 구할 수 있고 이미 구한 값을 호출함으로써 중복되는 연산을 막을 수 있다. 따라서 다이나믹 프로그래밍을 활용한다면 기존의 O(n^2)의 문제를 O(n)의 시간복잡도 만으로 해결 할 수 있다.

DP를 위한 조건

1. Optimal substructure (부분 반복 문제) : 반복되는 연산의 값을 저장하여 재활용하는 방식의 알고리즘 이므로 이전에 본 피보나치 문제처럼 동일한 작은 문제들이 반복되어 나타날 때 DP를 사용 할 수 있다.
2. Overlapping problems (최적 부분 구조) : 이전 문제들의 값을 반복문을 돌려 다음 값을 구해 나가는 방식의 알고리즘으로 부분 문제에서 구한 최적 결과가 전체 문제에서도 동일하게 적용될 수 있을 때 DP를 사용 할 수 있다.

⭐️동적 계획법의 과정⭐️

1. 변수간의 상관관계 정의하기
2. 최적해를 구할 수 있는 점화식 구하기
3. 최적해를 위한 기저 상태 저장하기
4. 반복문 혹은 재귀 중 적합한 풀이를 선정하여 구현하기

문제를 통해 위의 과정을 구해보자 다음은 다이나믹 프로그래밍에서 가장 유명한 문제 중 하나인 평범한 배낭 문제에 대한 해설이다. (https://www.acmicpc.net/problem/12865)

1. 변수간의 상관관계 정의하기

   문제를 해결하기 위해 고려해야 하는 변수는 크게 두가지로 w(무게)와 v(가치)이다. 무게는 최대 하중 k이하이면 되고 v의 합이 최대가 되어야 한다. 따라서 배낭의 리미트 k를 늘려나가면서 해당 물건을 넣었을 때 넣지 않았을 때를 고려하여 문제를 해결 할 수 있을 것이다.

2. 최적해를 구할 수 있는 점화식 구하기
   물건 하나씩 넣을지 말지를 판단하면서 현재 하중에서 버틸 수 있는 최대 가치를 구할 것이다. 두 가지 경우로 나누어 생각 할 수 있을 것이다.

   먼저 현재 물건이 최대 하중보다 가벼울 때이다. 이때는 현재 물건을 가방에 넣을 수 없으므로 이전 물건까지 연산한 값을 그대로 가져오면 될 것이다. 따라서 점화식으로는 dp[i][w]=dp[i-1][w]로 표현 할 수 있다.

   다음 경우는 현재 물건의 무게가 최대 하중보다 작거나 같을 때이다. 이때는 물건을 넣을 경우와 넣지 않았을 경우 중 더 높은 값을 가져오면 될 것이다. (물건을 넣을 때 현재 물건의 하중만큼의 빈공간이 있어야 하므로 dp[i-1][w-W[i]]값에 가치를 더하면 된다.) 즉 dp[i][w]=max(dp[i-1][w-W[i]]+V[i],dp[i-1][w]) 점화식으로 표현 할 수 있다.
   

3. 최적해를 위한 기저 상태 저장하기

   이 문제에서 기저 상태는 배낭에 아무것도 없을 경우 0으로 초기화 해주면 된다.
   

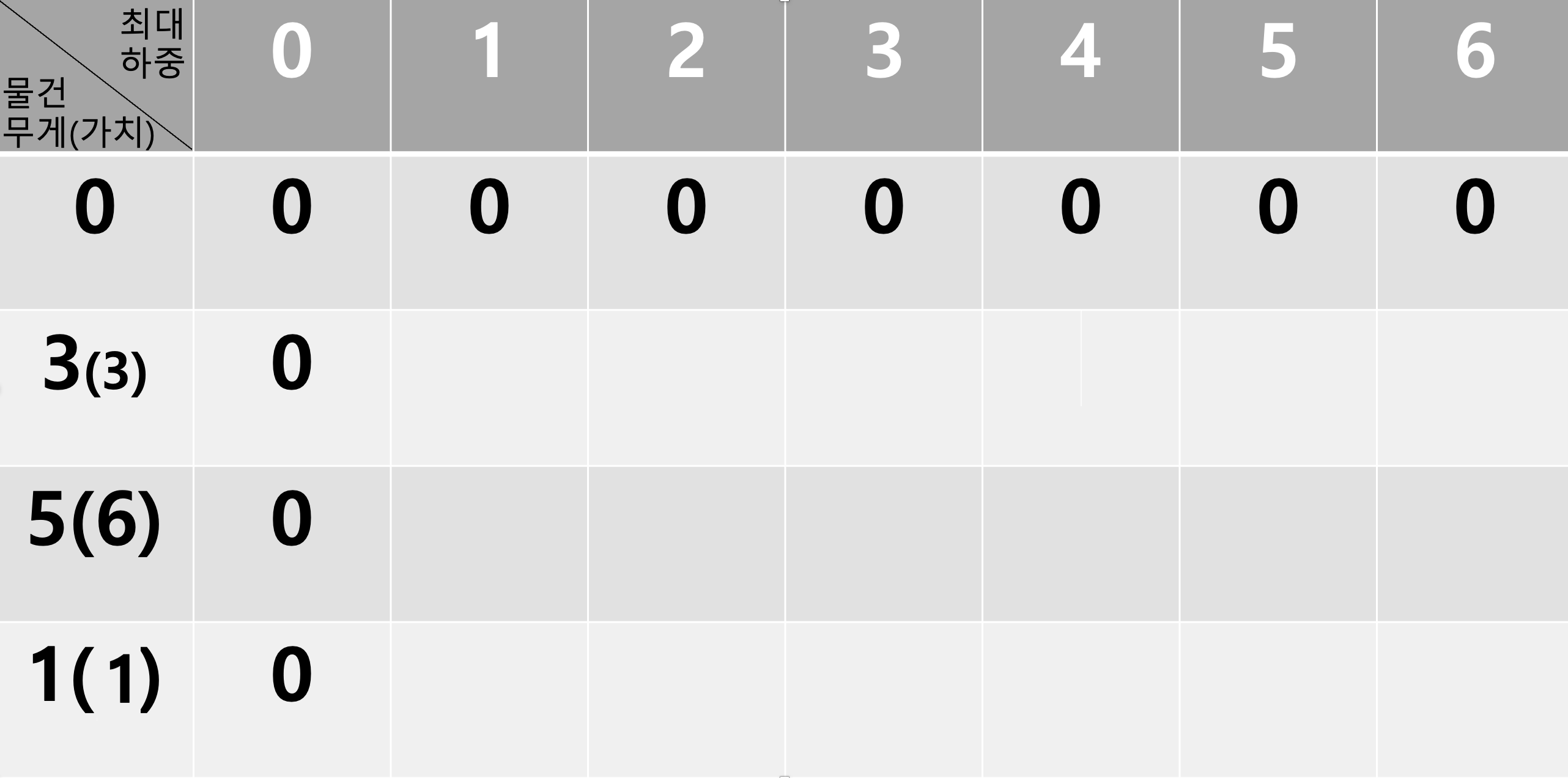
4. 반복문 혹은 재귀 중 적합한 풀이를 선정하여 구현하기

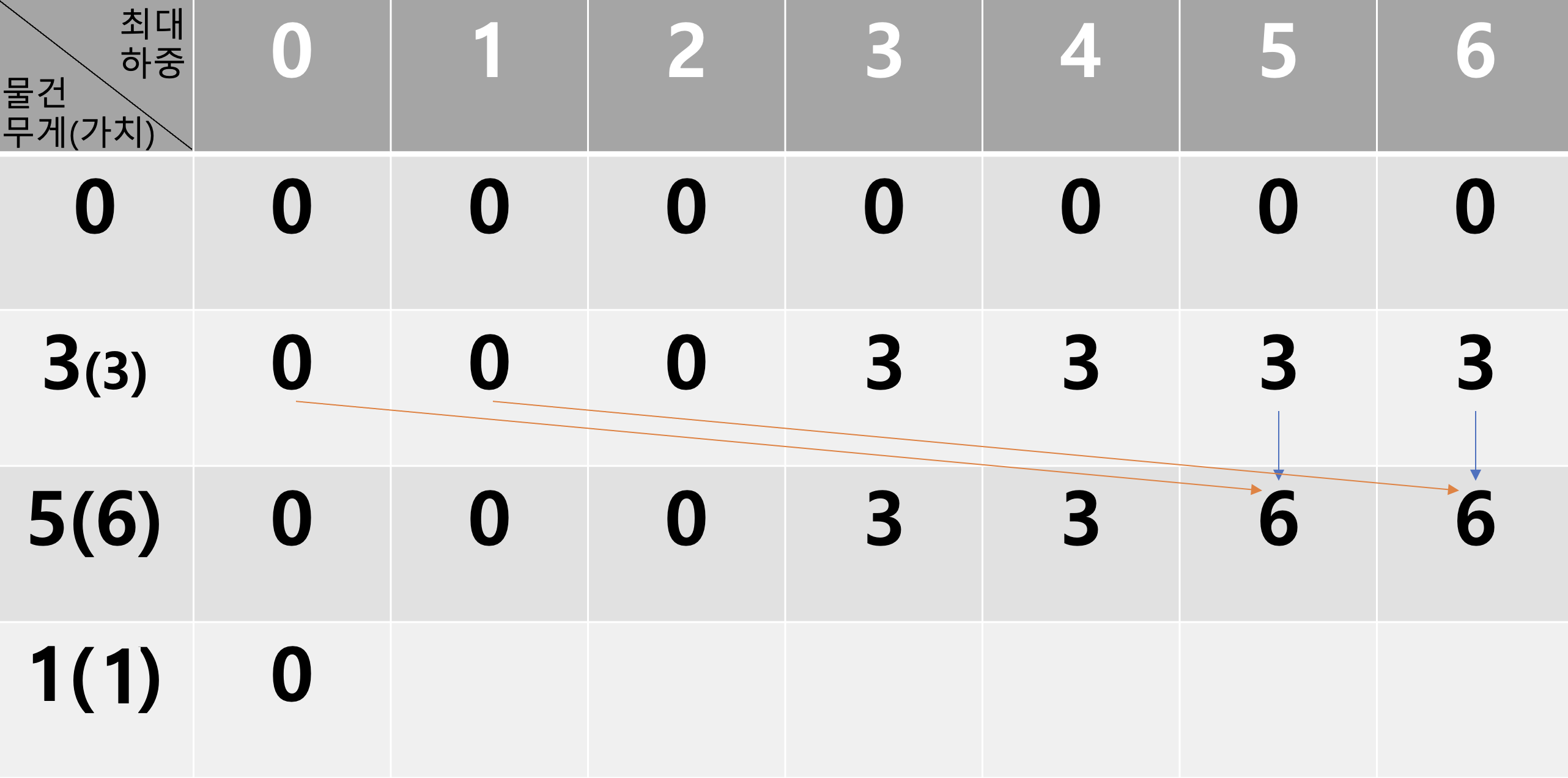
   반복문으로 위의 점화식을 돌리게 되면 배열이 다음과 같이 저장 될 것이다
   

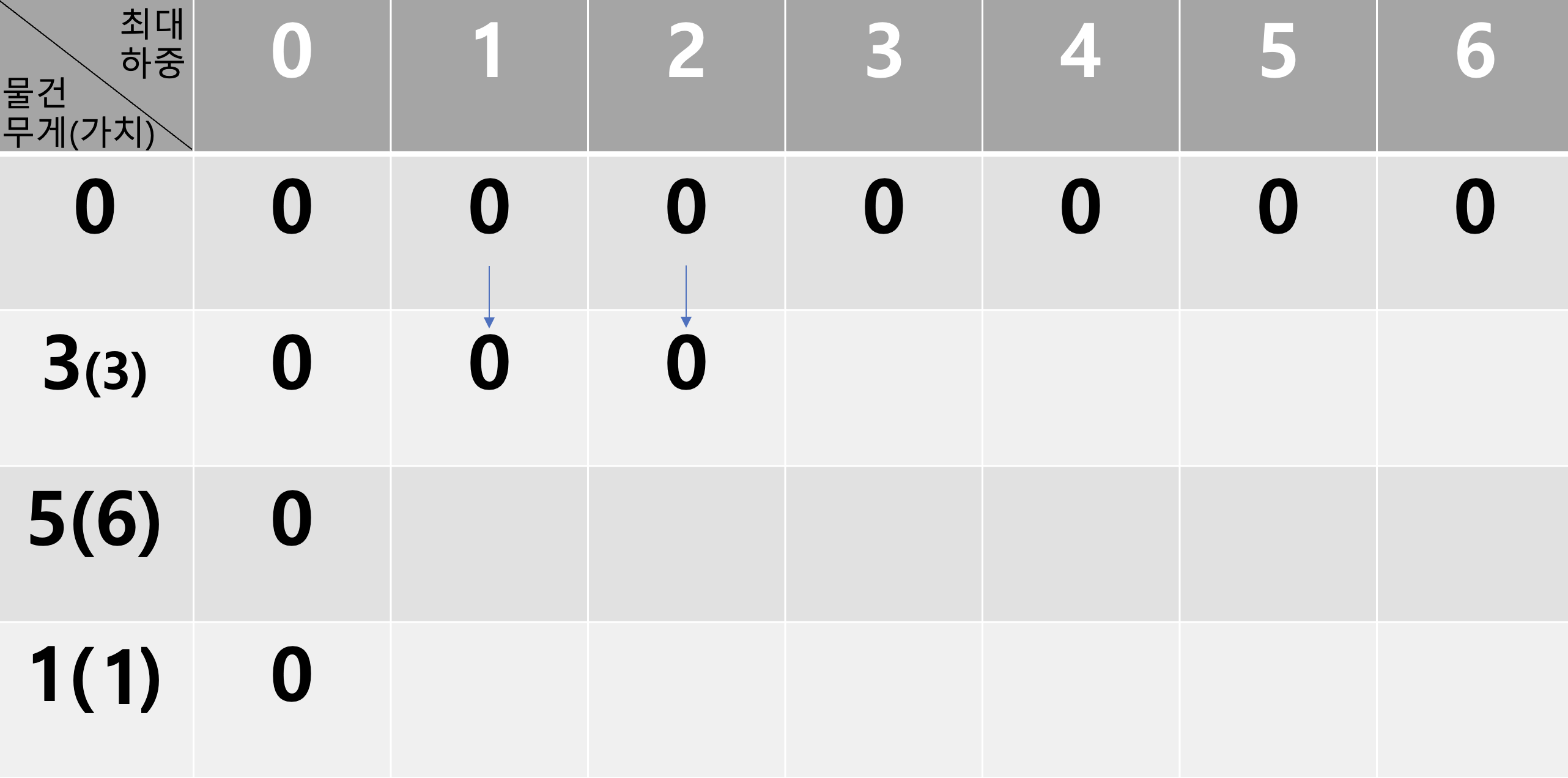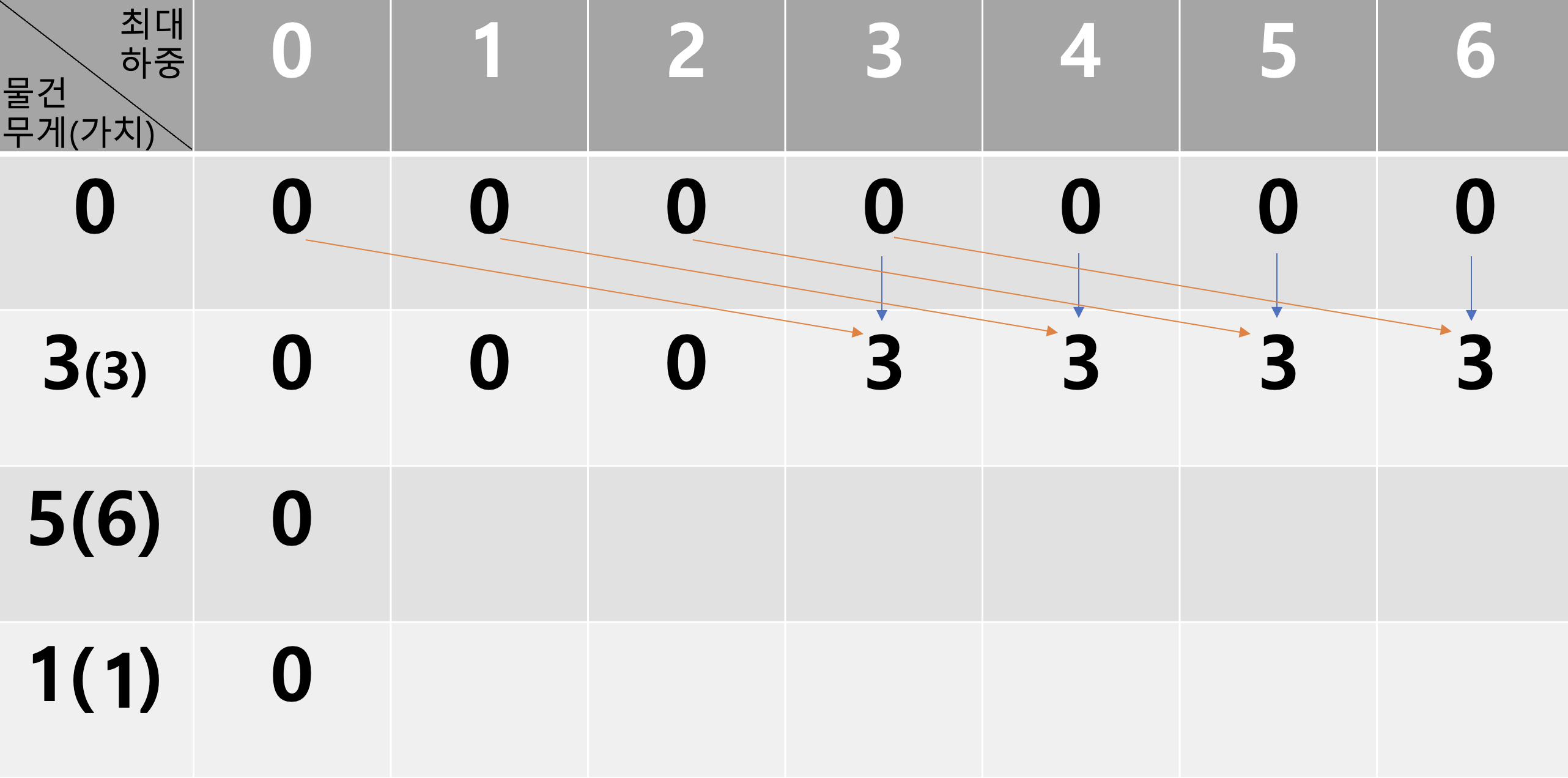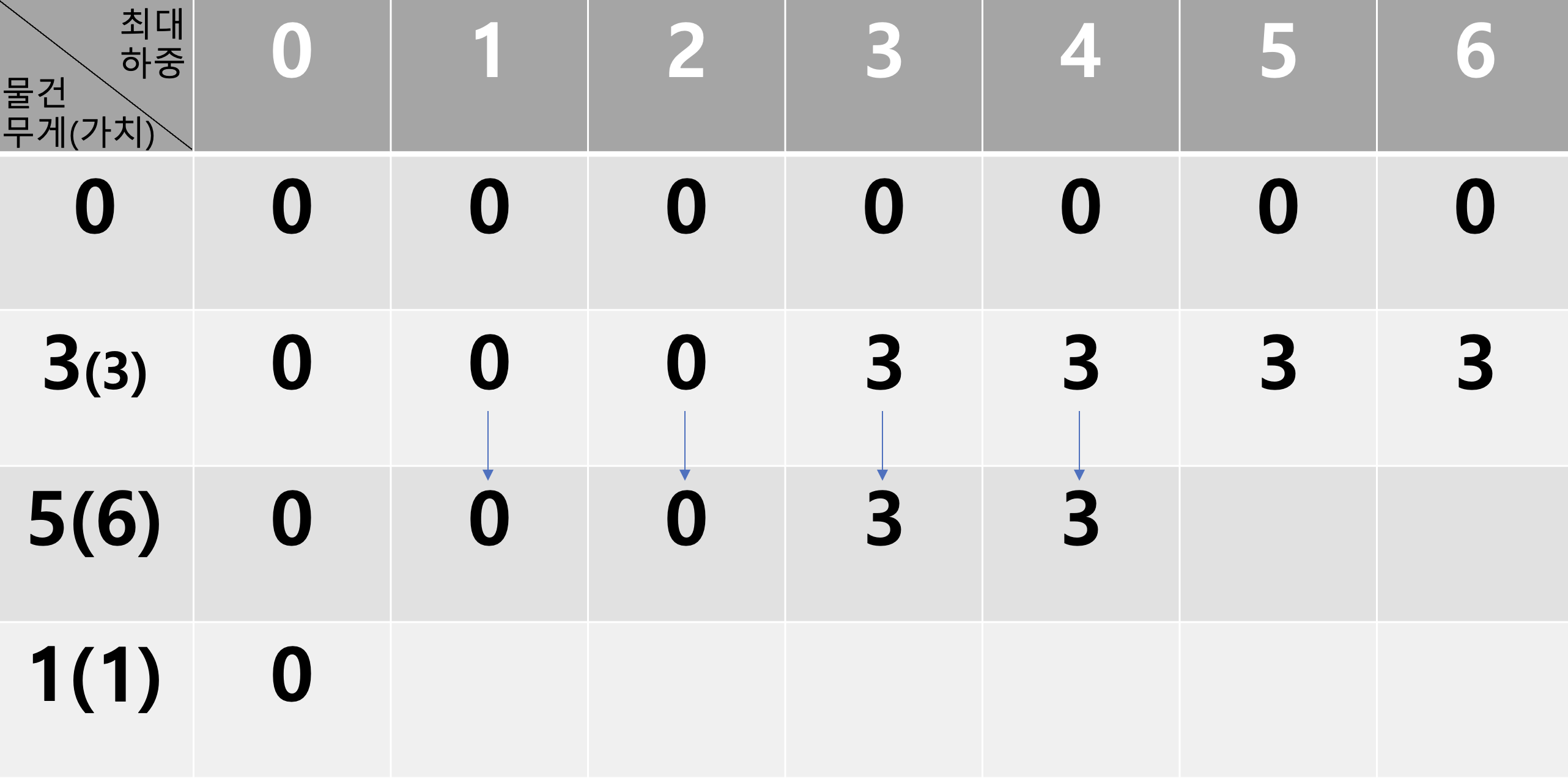
하중 리미트 값보다 현재 물건이 가벼울 때 현재 물건을 넣을 수 있을 때(노란선 : 물건을 넣었을 때 / 파란선 : 물건을 넣지 않았을 때) 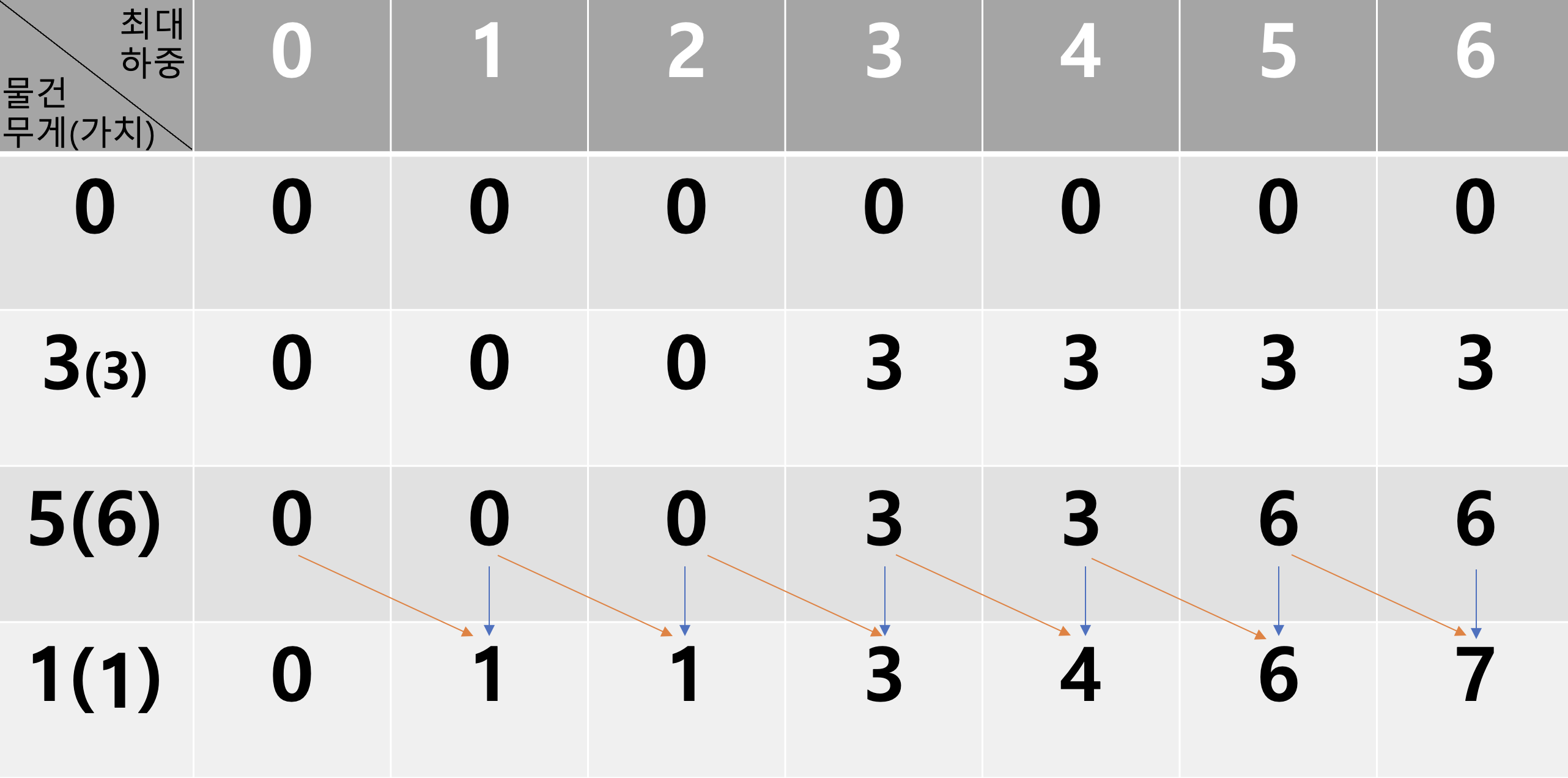따라서 무게 5와 1의 물건을 넣었을 때 가치가 7로 최대가 됨을 구할 수 있다.

전체 코드

#include<iostream>
#include<algorithm>
using namespace std;

int dp[101][100001];
int W[101];
int V[101];

int main() {
	int n,k;
	cin >> n >> k;
	for(int i=1; i<=n; i++) {
		cin >> W[i];
		cin >> V[i];
	}
	for(int i=1; i<=n; i++) {
		for(int w=0; w<W[i]; w++)
			dp[i][w]=dp[i-1][w]; 
		for(int w=W[i]; w<=k; w++)
			dp[i][w]=max(dp[i-1][w-W[i]]+V[i],dp[i-1][w]);
	}
	cout << dp[n][k] << '\n';
}