누적합(Prefix Sum) / boj (17390, 11660)

정의

누적합은 구간의 누적값을 배열에 저장함으로써 일부 구간의 구간합을 빠르게 구하기 위한 알고리즘이다.

목적

누적합 알고리즘을 특정 구간의 합을 여러 번 계산할 때 매우 유리하다.

아래 표를 보면서 어떤 이유로 누적합 알고리즘을 사용하는지 알아보자!

index	1	2	3	4	5	6
num	3	5	7	2	4	5
sum	3	8	15	17	21	26

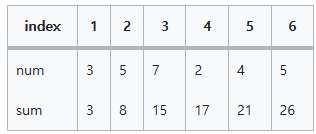
위의 표의 가장 윗 줄은 배열의 인덱스이고 num은 숫자 배열, sum은 처음 숫자부터 해당 구간까지의 합이다. 보기 쉽게 6칸의 숫자 배열로 작성 했지만 배열의 크기가 N(1≤ N ≤ 500,000)이라고 가정하자! 우리는 Q(1≤ Q ≤ 100,000)번 변수i, j(1≤ i < j ≤ N)의 값을 입력 받아 i부터 j까지의 합을 구하고 싶다.

그렇다면 이 문제를 어떻게 해결 할 수 있을까? 가장 간단한 방법으로는 i, j를 입력 받을 때마다 for(int k = i, k ≤ j, k++) 이와 같이 반복문을 사용하여 값을 더하는 방식으로 해결 할 수 있을 것이다. 그러나 시간 복잡도를 고려한다면 쿼리가 최대 100,000번 반복되고 구간합을 구하기 위한 반복문이 최대 500,000번 반복되므로 최악의 시간 복잡도 O(N) = O(Q * N) 는 50,000,000,000이라는 어마어마한 시간 복잡도를 가지게 될 것이다.

다른 방법으로는 누적된 값을 활용하는 방법이 있을 것이다. num 배열의 값을 입력 받을 때 num 배열과 같은 크기의 sum배열을 만들어 누적된 값을 더한다면 위와 같이 배열에 저장될 것이다. 그렇다면 3~5번째 인덱스의 구간합은 num[3] + num[4] + num[5]로 계산 할 수도 있겠지만 sum[5] - sum[2]로 계산 할 수 있을 것이다. 따라서 sum[j] - sum[i-1]의 수식으로 구간합 구한다면 시간 복잡도를 쿼리의 수 Q만으로 구간합 문제를 해결 할 수 있다!

누적합 풀이 과정

실제 문제를 통해 누적합 문제를 해결하는 과정을 알아보자! 근본적인 원리는 똑같지만 1차원 배열 뿐만 아니라 2차원 배열의 형태로도 자주 출제되기 때문에 두 가지 문제를 준비해 보았다.

17390번: 이건 꼭 풀어야 해! (acmicpc.net) 1차원 누적합의 귀여운 문제가 있어서 가져와 보았다.

1. 누적합 배열 구하기

   먼저 반복문을 통해 누적합 배열을 채운다. 아래와 같이 할 수 있을 것이다.

   for(int i=1; i<=N; i++) S[i]=S[i-1]+B[i];

2. 구간의 시작과 끝 입력 받아 누적합 차이 계산하기

   L, R이 각각 시작과 끝이라면 S[R]-S[L-1]이 결과 값이 된다 배열의 시작인 1이 들어오더라도 해당 수식을 그대로 사용하기 위해 배열을 0번째 부터 채우지 말고 한칸을 비워두는 것이 편리하다!

   printf("%d\n",S[R]-S[L-1]);

전체 코드(boj 17390)

#include<iostream>
#include<algorithm>
using namespace std;

int N,M;
int A[300101], S[300101], B[300101];

int main() {
	scanf("%d %d",&N,&M);
	for(int i=1; i<=N; i++) {
		scanf("%d",&A[i]);
		B[i]=A[i];
	}
	sort(B+1,B+N+1);
	for(int i=1; i<=N; i++)
		S[i]=S[i-1]+B[i];
	while(M--) {
		int L,R;
		scanf("%d %d",&L,&R);
		printf("%d\n",S[R]-S[L-1]);
	}
}

---

11660번: 구간 합 구하기 5 (acmicpc.net) 2차원 배열을 이용한 누적합 문제이다.

num(I,j)	1	2	3	4	5
1	1	0	0	1	0
2	0	1	1	0	1
3	1	1	0	1	0
4	0	1	0	1	0

1. 누적합 배열 구하기

   구간합을 구할 원리를 찾아보자! 먼저 num(4,3)까지의 구간합 범위는 아래 영역이 될 것이다.

   num(I,j)	1	2	3
   1	1	0	0
   2	0	1	1
   3	1	1	0
   4	0	1	0

   해당 영역 넓이는 아래 두 영역의 합에서 공통된 범위를 뺌으로서 구할 수 있을 것이다.

   num(I,j)	1	2	3
   1	1	0	0
   2	0	1	1
   3	1	1	0

   
   

   num(I,j)	1	2
   1	1	0
   2	0	1
   3	1	1
   4	0	1

   따라서 S[i][j] = S[i-1][j] + S[i][j-1] - S[i-1][j-1] + A[i][j]; 해당 수식으로 누적합을 구할 수 있을 것이다.

위 공식으로 구한 누적합은 아래와 같다

num(i,j)	1	2	3	4	5
1	1	1	1	2	2
2	1	2	3	4	5
3	2	4	5	7	8
4	2	5	6	9	10

2. 구간의 좌표 입력 받아 구간합 구하기

   위에서 구한 누적합의 결과 (2,2)에서 (3,4)까지의 구간합을 구하고 싶다면 어떻게 해야할까?

   먼저 (3,4)의 누적합의 값은 아래 영역의 합일 것이다.

   num(i,j)	1	2	3	4
   1	1	1	1	2
   2	1	2	3	4
   3	2	4	5	7

   그 중에 필요 없는 영역인 아래 두 누적합 영역(1,4),(3,1)을 빼고 겹치는 부분(1,1)을 더해 준디면 원하는 영역인 (2,2)~(3,4)의 구간합을 구할 수 있다.

   num(i,j)	1	2	3	4
   1	1	1	1	2

   
   

   num(i,j)	1
   1	1
   2	1
   3	2

따라서 다음 수식으로 구할 수 있을 것이다.

구간합의 영역 : S[x2][y2] - S[x1-1][y2] - S[x2][y1-1] + S[x1-1][y1-1]

전체 코드(boj 11660)

#include<bits/stdc++.h>
using namespace std;

int N,M;
int A[1025][1025];
int S[1025][1025];

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cin >> N >> M;
	for(int i=1; i<=N; i++)
		for(int j=1; j<=N; j++)
			cin >> A[i][j];
	for(int i=1; i<=N; i++)
		for(int j=1; j<=N; j++)
			S[i][j] = S[i-1][j] + S[i][j-1] - S[i-1][j-1] + A[i][j];
	int x1,y1,x2,y2;
	for(int i=0; i<M; i++) {
		cin >> x1 >> y1 >> x2 >> y2;
		x1--; y1--;
		cout << S[x2][y2] - S[x1][y2] - S[x2][y1] + S[x1][y1] << '\n';
	}
}