수학, 소수 판별 알고리즘

모듈러 연산

1. (A+B)%M = ((A%M) + (B%M)) % M
2. (AB)%M = ((A%M) (B%M)) % M
3. (A-B)%M = ((A%M) - (B%M)) % M
4. A%M == B%M → (A^n)%M == (B^n)%M

소수 판별

자연수 n(n>1)이 소수임을 판별하기 위한 방법

for(int i=2; i<n; i++) {
	if(n%i == 0) {
		cout << "소수가 아님\n";
		return 0;
	}
}
cout << "소수임\n";

위와 같이 n이하의 수들을 하나씩 나누어 보면서 나눠지는 값이 있다면 소수가 아니다라는 정의를 내릴 수 있다. 그러나 자연수 n이 소수인지 판별하기 위해 n 이하의 모든 수로 나누어야만 하는가?

for(int i=2; i*i<=n; i++) {
	if(n%i == 0) {
		cout << "소수가 아님\n";
		return 0;
	}
}
cout << "소수임\n";

위의 코드도 n이 소수인지 판별하기에 충분하다. 어떻게 가능한가? 나누어 진다는 것은 두 수의 곱으로 나타 낼 수 있기 때문이다. 36이라는 숫자를 생각해보자! 36은 (2x18), (3x12), (6x6)으로 나타낼 수 있다. 루트 36인 6 이상의 수인 12와 18로 나누어졌다는 것은 이미 2와 3으로 나누어졌다는 의미이다. 따라서 ii 이전에 나누어 지지 않았다는 것은 ii 이후에도 나누어 지지 않는다는 의미이다.

유클리드 호제법

두 양의 정수 a,b(a > b)에 대하여 a = bq + r (0≤ r < b)이라 하면 a,b의 최대 공약수는 b,r의 최대 공약수와 같다

int gcd(int a,int b) { // 최대 공약수
	if(b==0)
		return a;
	else
		return gcd(b,a%b);
}

int lcm(int a, int b) { // 최소 공배수
	return a/gcd(a,b)*b;
}

에라토스테네스의 체

주어진 범위 내의 배열에서 소수가 아닌 수를 제거해 나가며 소수만 남겨두는 알고리즘

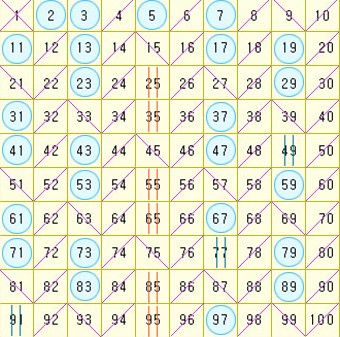
이미지 출처 : https://blog.naver.com/pascal_edu/152292594

for(int i=2;i * i<=Max_n;i++){
	if(arr[i]) continue; //i가 소수가 아니라면 이미 i의 배수는 방문함
	for(int j=i * i;j<=Max_n;j+=i){
		arr[j] = true;
	}
}