Camera Calibration

eric9687·2023년 8월 20일

Camera Calibration

카메라 캘리브레이션(camera calibration)은 카메라의 내부 파라미터와 외부 파라미터를 정확하게 계산하는 과정을 말합니다. 이를 통해 카메라의 이미지 센서와 실제 세계(world) 간의 관계를 정확하게 매핑할 수 있게 되며, 이를 통해 영상에서 발생하는 왜곡과 오차를 보정할 수 있습니다.

쉽게 말해서, 사진(이미지)에 있는 수많은 2D점들과 world 공간상의 3D 좌표들간의 관계를 알아가는 것인데, 이 관계는 카메라의 외부/내부 파라미터에 의해 결정되고, 그 파라미터들을 찾는 과정을 camera calibration이라 합니다.

Back ground

Internal/External paremeters

Internal parameters
: 카메라나 렌즈 시스템의 focal length, optical center, radial distortion coefficient에 관한 parameter.
- 초점 거리 (focal length) - $f_x, f_y$
  - 렌즈의 초점점(렌즈 중심)에서 이미지 센서까지의 거리
  - 카메라 렌즈의 화각, 확대/축소 정도들을 결정하는 요소
  - 밀리미터(mm)로 표현
    - 거리가 짧으면 렌즈가 넓을 영역을, 길면 좁은 영역을 포착
  - 현대 카메라의 경우, 웬만하면 $f_x=f_y$
- 주점 거리 (principal point) - $c_x, c_y$
  - 카메라에서 이미지가 생성되는 곳의 중심점
  - 카메라의 이미지 센서와 렌즈 광학 축의 교차점을 나타내는 점
  - 핀홀에서 이미지 센서에 내린 수선의 발의 영상 좌표
- 비대칭 계수 (skew coefficient) - $skew_c = tan\alpha$
  - 이미지 센서의 픽셀 격자가 수직 및 수평 방향으로 정렬되지 않은 경우를 나타내는 값 (비대칭 정렬 정도)
  - 0에 가까울수록 픽셀 격자는 대칭적으로 정렬되어 있고, 값이 클수록 비대칭적으로 기울어져 있는 것
External parameters
- 카메라와 촬영 대상 객체간의 상대적인 위치와 방향을 나타내는 parameter
  - 그 위치와 방향을 orientation이라고 함.
- 어떻게 구하는가? => camera calibration을 통해서 (calibration tool을 통해서)
  - 일반적인 절차
    - 패턴 또는 물체 준비
      - 논문이나 demo영상에 보이는 체크보드가 이에 해당
    - 다양한 각도와 위치에서 이미지 촬영
    - 특징점 검출
      - 페턴의 특징점/ 물체의 특징점
    - 외부 파라미터 추정
    - 예측 및 검증

Geometry of Image Formation

우선, 3D좌표살의 한 점이 어떻게 이미지상에 대응되는 지 알아야합니다. 그러려면, 그전에 좌표계(coordinate system)에 대해서 이해하고 넘어가야 합니다.

쉽게 이해하기 위해서, 한 공간에 카메라가 설치되어 있다고 합시다. 그리고 그 공간에 하나의 3D 점이 있고, 카메라를 통해서 그 점을 pixel 좌표 ( $u,v$ )를 찾고자하는 것이 목표라고 합니다.

좌표계에는 World Coordiate System, Camera Coordiate System, Image Coordiate System이 있는데요. 더 자세히는 아래에서 봅시다.

World Coordiate System
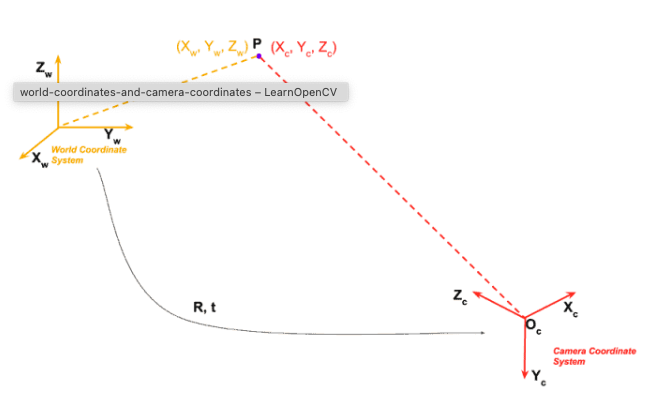
- 그림에서 노란색에 해당
- Origin: 공간의 한 구석을 origin (0, 0, 0)으로 정의
- X,Y,Z axes: 위의 그림처럼 X,Y를 정의하고 바닥과 수직인 축을 Z로 정의
- 정의된 공간상의 한점의 Origin에서 얼마나 떨어져있는가를 ( $X_W,Y_W,Z_W$ )로 표현하고, 그 좌표계를 World Coordiate System이라 정의
Camera Coordiate System

위에서 world좌표가 정의되었고, 그 공간에 카메라도 위치할 것인데, 그 카메라가 가많이 한 곳에만 있을 수 있으면 좋으련만...그렇지 않겠죠? 게다가 다양하게 회전도 할 수 있을 것입니다. 따라서 카메라 중심의 카메라 좌표계도 정의가 되어야하죠.

카메라가 world상의 임의의 위치 $t = (t_X, t_Y, t_Z)$ 에 있고, $R=(yaw, ptich, roll)$ 만큼 회전되어 있을때, 카메라 좌표 $(X_C, Y_C, Z_C)$ 는 아래 처럼 표현 할 수 있습니다.
- $\begin{bmatrix} X_C \\\\ Y_C \\\\ Z_C \end{bmatrix}=R\begin{bmatrix} X_w \\\\ Y_w \\\\ Z_W \end{bmatrix}+t$
- 하지만 Extrinc matrix는 $3\times 4$ 이기 때문에, 아래처럼 바꿔줍니다.
- $\begin{bmatrix} X_C \\\\ Y_C \\\\ Z_C \end{bmatrix}=[R|t]\begin{bmatrix} X_w \\\\ Y_w \\\\ Z_W \\\\ 1 \end{bmatrix}$
- 여기서, extrinsic matrix를 다른 방법으로 $P$ 라고 표현 합니다.
Image Coordinate System

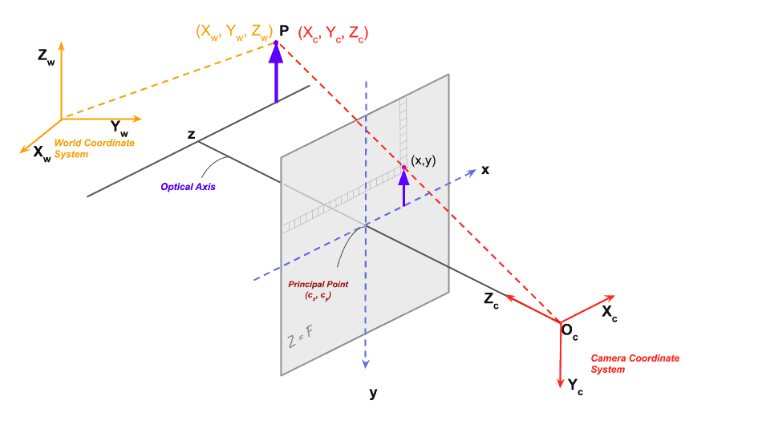
평행이동과 회전이 적용된 카메라를 통해서 공간에 있는 점을 이미지산에 project한다고 했을때, 그 점이 존재하는 좌표계를 Image Coordinate System, 영상 좌표계이라고 합니다.

optical center (pin hole)을 $O_C$ 라고 하고, 이미지 평면(image plane)위에 점이 찍혀있다는 가정으로 시작해봅니다. 센서로 부터 읽힌 이미지는 180도 돌아간 상태로 있고, image plane은 optical center 바로 앞에 있습니다.그리고 image plane은 $f$ (focal length)만큼 optical center로 부터 떨어져 있죠.

그럼, 3D점 ( $X_c, Y_c, Z_c$ )가 아래식으로 project하여 이미지상에 ( $x,y$ )로 표현할 수 있죠.
- $x=f\frac{X_c}{Z_c}, y=f\frac{Y_c}{Z_c}$
- 다르게 표현해보면, $\begin{bmatrix} x' \\\\ y' \\\\ z' \end{bmatrix}=R\begin{bmatrix} f \ 0 \ 0 \\\\ 0 \ f\ 0 \\\\ 0 \ 1 \ 1 \end{bmatrix}\begin{bmatrix} X_c \\\\ Y_c \\\\ Z_c \end{bmatrix}$ 이 됩니다.
- 여기서 Intrinsic Matrix $K=\begin{bmatrix}f \ 0\ 0 \\\\ 0 \ f\ 0 \\\\ 0 \ 0 \ 1\end{bmatrix}$ 을 얻을 수 있습니다.
- 하지만 이미지가 정사각형이 아닐 수 있으니, $f$ 를 $f_x,f_y$ 로 나눌 수 있고요.
  
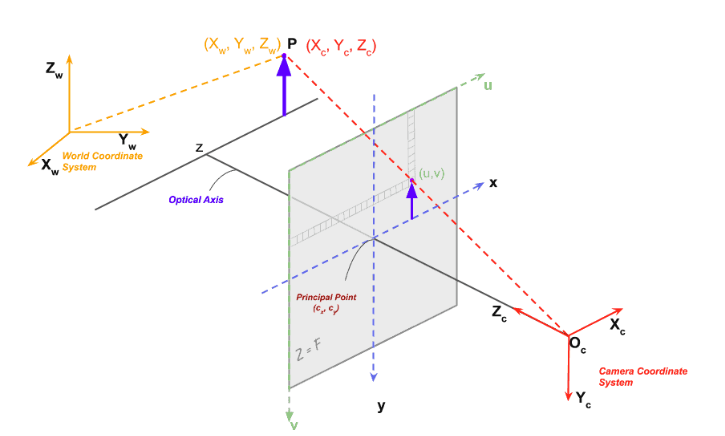
  다음은 여기서 optical center $(c_x,c_y)$ 가 이미지 중간에 있다는 가정을 없애고, 비대칭( $skew_c, \gamma$ )도 존재한다고 하면, Intrinsic Matrix $K=\begin{bmatrix}f_x \ \gamma\ c_x \\\\ 0 \ f_y\ c_y \\\\ 0 \ 0 \ 1\end{bmatrix}$ 가 됩니다.
  $\begin{bmatrix} u' \\\\ v' \\\\ w' \end{bmatrix}=\begin{bmatrix}f_x \ \gamma\ c_x \\\\ 0 \ f_y\ c_y \\\\ 0 \ 0 \ 1\end{bmatrix}\begin{bmatrix} X_c \\\\ Y_c \\\\ Z_c \end{bmatrix}, u=\frac{u'}{w'},v=\frac{v'}{w'}$

Relationship between World coordinate & Image coordinate

위에서 World Coordiate System, Camera Coordiate System, Image Coordiate System를 이해하고 나면, world좌표와 image좌표간의 관계식은 아래와 같이 정리할 수 있습니다.

\begin{bmatrix} u' \\\\ v' \\\\ w' \end{bmatrix}=\begin{bmatrix}f_x \ \gamma\ c_x \\\\ 0 \ f_y\ c_y \\\\ 0 \ 0 \ 1\end{bmatrix}\begin{bmatrix}r_{11} \ r_{12}\ r_{13} \ t_1 \\\\ r_{21} \ r_{22}\ r_{23} \ t_2 \\\\ r_{31} \ r_{32}\ r_{33} \ t_3\end{bmatrix}\begin{bmatrix} X_w \\\\ Y_w \\\\ Z_w \end{bmatrix}, u=\frac{u'}{w'},v=\frac{v'}{w'}

calibration

위의 배경 지식을 알고, 드디어 어떻게 캘리브레이션을 하는지를 보려고 합니다.

calibration methods

Calibration pattern
- 다양한 관점에서 물테나 패턴을 촬영하여 수행하는 방법
- 체크보드나 원모양 패턴으로 할 수 있음
Geometric clues
- 직선이나 소실점등을 알고 있는 상태애서 수행하는 방법
Deep Learning based
- 이미지 한장만 있을때에 수행할 수 있는 방법

calibration steps

Define real world coordinates with check board
체크보드를 벽에 붙임으로 world 좌표를 정해놓습니다. 체크보드의 사각형 모서리의 점들을 3D 점들이라고 하고, 하나의 점을 world 좌표계의 origin으로 설정합니다. $X_W,Y_W$ 는 벽을 따라 있고, $Z_W$ 는 그 벽에 수직이라 설정합니다. 그럼, 체크보드는 XY 평면에 있게 됩니다.
calibration과정에서 3D 점들( $X_w,Y_w,Z_w$ )과 그에 대응하는 이미지상의 위치 ( $u,v$ ) 세트들로 camera parameter를 얻습니다.
이때ㅐ, 3D 점들을 알고 있는 차원상의 다양한 방향에서 촬영합니다. 모든 꼭지점들의 world 좌표는 체크보드위에 있기때문에, $Z_w$ 는 0으로 설정될 수 있습니다. 그리고, 그 점들은 다 같은 간격으로 떨어져 있기 때문에, 한점을 알면 모든 점들을 쉽게 정의할 수 있습니다.
- 체크보드를 많이 사용하는 이유는?
  이미지에서 모서리를 뚜렷하게 알 수 있고, 모서리가 급격한 기울기를 가지기 때문에 위치 파악이 쉽습니다. 그리고, 모서리가 서로 교차되어 만들어지기 때문입니다.
Capture multiple images of the checkerboard from different viewpoints
체크보드는 가만히 둔 상태로 여러 방향에서 많은 이미지들을 촬영하거나 카메라를 고정시키고 체크보드를 움직이거나 둘 중 하나를 선택하여 실행합니다.
Find 2D coordinates of checkerboard
- Find checkerboard corners
  OpenCV의 내장함수 findChessboardCorners를 사용하여 코너 좌표를 반환 받습니다.
```
# C++
bool findChessboardCorners(InputArray image, Size patternSize, OutputArray corners, int flags = CALIB_CB_ADAPTIVE_THRESH + CALIB_CB_NORMALIZE_IMAGE )

# python
retval, corners = cv2.findChessboardCorners(image, patternSize, flags)
```
- Refine checkerboard corners
  정밀도 있는 좋은 calibration 결과를 얻기 위해서, 서즐 픽셀 수준의 정확도를 가져야합니다. OpenCV의 함수 cornerSubPix를 이용하여 origin 위치에서 가까운 이웃 점들에서 가장 적합한 corner 위치를 찾습니다. 반복 횟수를 정해 반복하거나 종료 기준까지 알고리즘을 수행합니다.
```
# C++
void cornerSubPix(InputArray image, InputOutputArray corners, Size winSize, Size zeroZone, TermCriteria criteria)

# python
cv2.cornerSubPix(image, corners, winSize, zeroZone, criteria)
```

Calibrate Camera
world 좌표계의 3D 점들과 그들의 이미지상의 2D 위치를 OpenCV의 CalibrateCamera에 적용합니다.

# C++
double calibrateCamera(InputArrayOfArrays objectPoints, InputArrayOfArrays imagePoints, Size imageSize, InputOutputArray cameraMatrix, InputOutputArray distCoeffs, OutputArrayOfArrays rvecs, OutputArrayOfArrays tvecs)


# python
retval, cameraMatrix, distCoeffs, rvecs, tvecs = cv2.calibrateCamera(objectPoints, imagePoints, imageSize)