본 포스팅은 카이스트 산업및시스템공학과 문일철 교수님의 Introduction to Artificial Intelligence/Machine Learning(https://aai.kaist.ac.kr/xe2/courses) 강의에 학습 정리입니다
Linear Function vs. Non-Linear Function
- linear function의 문제
- 확률 공리와 충돌
- 예시(데이터)에 느리게 반응
- logistic function이 더 나은 이유
- 확률 공리 유지
- Decision boundary에 빠른 반응
Sigmoid Function
- Sigmoid function의 특징
- Bounded
- Differential (부드럽게 되어있어서)
- Real Function
- Defined for all real inputs
- With positive derivative (증가하는 모양)
- Sigmoid function의 종류
- tanh(x)
- π2arctan(2πx)
- ...
Logistic Function
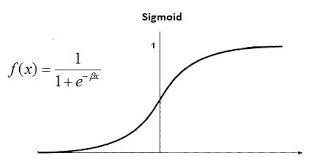
-
f(x)=1+e−x1
-
sigmoid function의 특징을 가지고 있다
-
derivative를 계산하기 쉽다 => optimization하기 좋다
-
logit function: logistic function의 역함수 f(x)=log(1−xx)
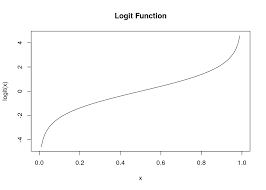
Logistic Function Fitting
f(x)=log(1−xx)
↓ logit function의 X domain은 likelihood P값에 대해서 모델링
↓ 한 것이라고, y domain은 input값(x)으로 모델링한다고 할 수 있다.
x=log(1−pp)
↓ fitting에 있어서 압축을 위해서 a를
↓ bias정보를 위해서 b를 추가
ax+b=log(1−pp)
↓ Linear regression의 trick을 이용해서
↓ f^=Xθ,θ=(XTX)−1XTY
Xθ=log(1−pp)=log(1−P(Y∣X)P(Y∣X))
Logistic Regression
- binomial 또는 multinomial 결과를 예측하는 확률적인 classifier
- 베루누이 실험이 주어졌을때,
- P(y∣x)=μ(x)y(1−μ(x))1−y
- μ(x)=1+e−θTx1=P(y=1∣x), logistic function ...(1)
- Xθ=log(1−P(Y∣X)P(Y∣X))→P(Y∣X)=1+eXθeXθ ...(2)
Parameter θ 구하는 방법
-
MLE에서의 θ
θ^=argmaxθP(D∣θ)
-
Maximum Conditional Likelihood Estimation, MCLE
-
θ^=argmaxθP(D∣θ)=argmaxθ∏1≤i≤NP(Yi∣Xi;θ)=argmaxθlog(∏1≤i≤NP(Yi∣Xi;θ))=argmaxθ∑1≤i≤Nlog(P(Yi∣Xi;θ))
-
P(Yi∣Xi;θ)=μ(Xi)Yi(1−μ(Xi))1−Yi
-
log(P(Yi∣Xi;θ))=Yilog(μ(Xi))+(1−Yi)log(1−μ(Xi))
=Yi{log(μ(Xi))−log(1−μ(Xi))}+log(1−μ(Xi))
=Yilog(1−μ(X−i)μ(Xi))+log(1−μ(Xi))
=YiXiθ+log(1−μ(Xi)) ,공식(2)사용
=YiXiθ−log(1+eXiθ),공식(1)사용
-
θ^=argmaxθ∑1≤i≤Nlog(P(Yi∣Xi;θ))
=argmaxθ∑1≤i≤N{YiXiθ−log(1+eXiθ)}
-
∂θ∂{YiXiθ−log(1+eXiθ)}
={∑1≤i≤NYiXi,j}+{∑1≤i≤N−1+eXiθ1×eXiθ×Xi,j}
=∑1≤i≤NXi(Yi−1+eXiθeXiθ)
=∑1≤i≤NXi,j(Yi−P(Y−i=1∣Xi;θ))=0
-
더 이상 진행할 수 가 없다...!
→ 근사(approximation)를 해야하는 것으로 귀결...(Gradient Descent Algorithm)
Gradient Descent/Ascent
- 함수 f(x)가 있고 초기 값을 x1이라고 할때,
- f(x)의 negative/positive방향을 잡아서
- 계속적으로 x1를 움직여서 f(x)가 계속해서 높아지도록/낮아지도록 하는 방법
- 위의 logistic regression에서는 초기값θ1을 잡아주고 iteratively하게 움직여서 θ를 optimize


