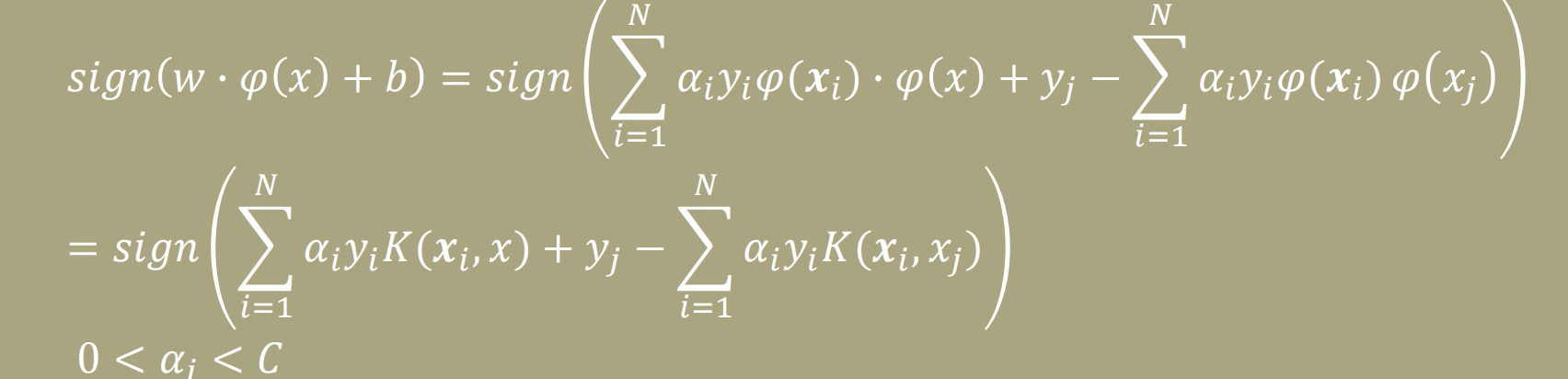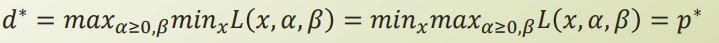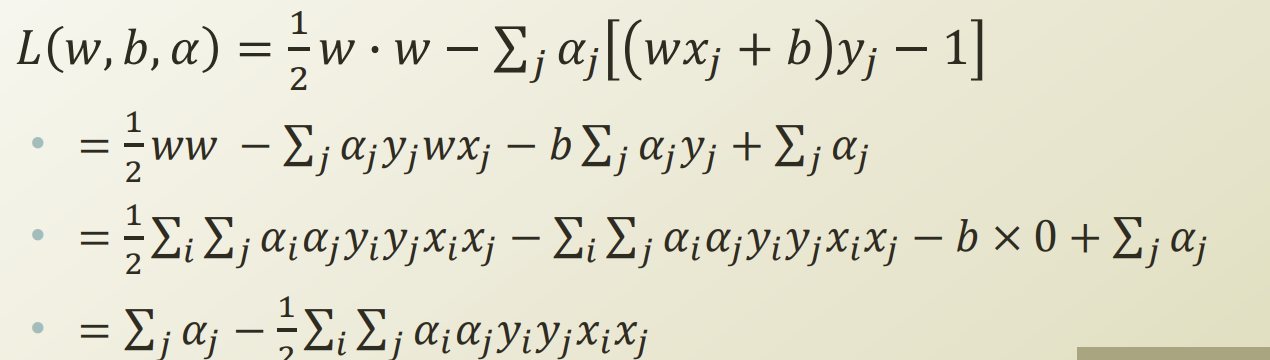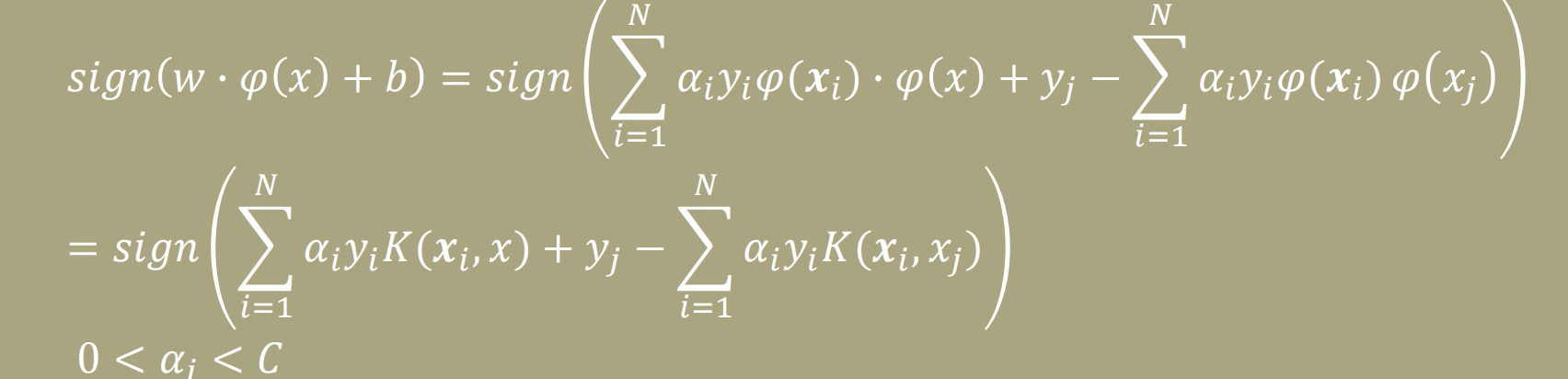본 포스팅은 카이스트 산업및시스템공학과 문일철 교수님의 Introduction to Artificial Intelligence/Machine Learning(https://aai.kaist.ac.kr/xe2/courses) 강의에 대한 학습 정리입니다.
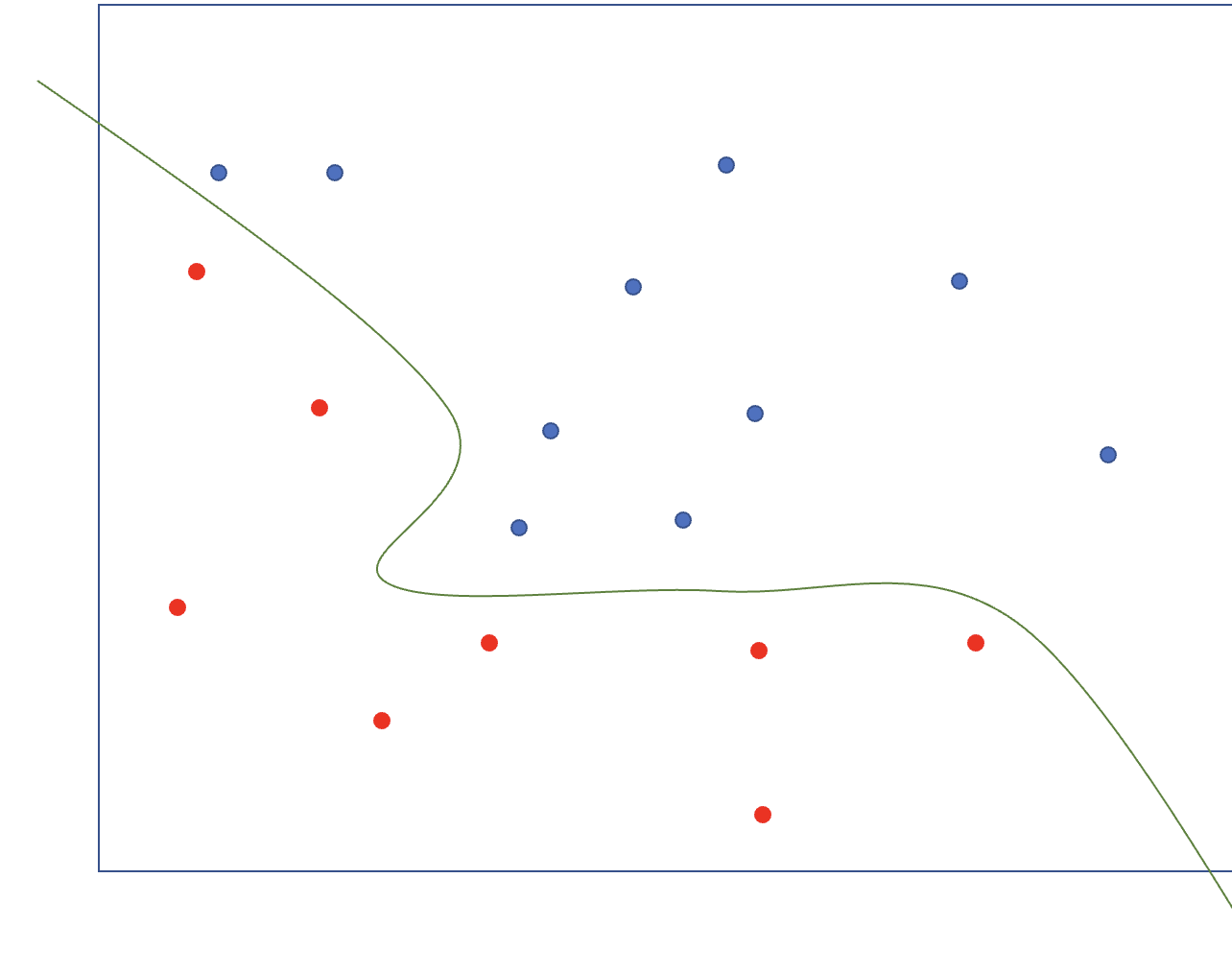
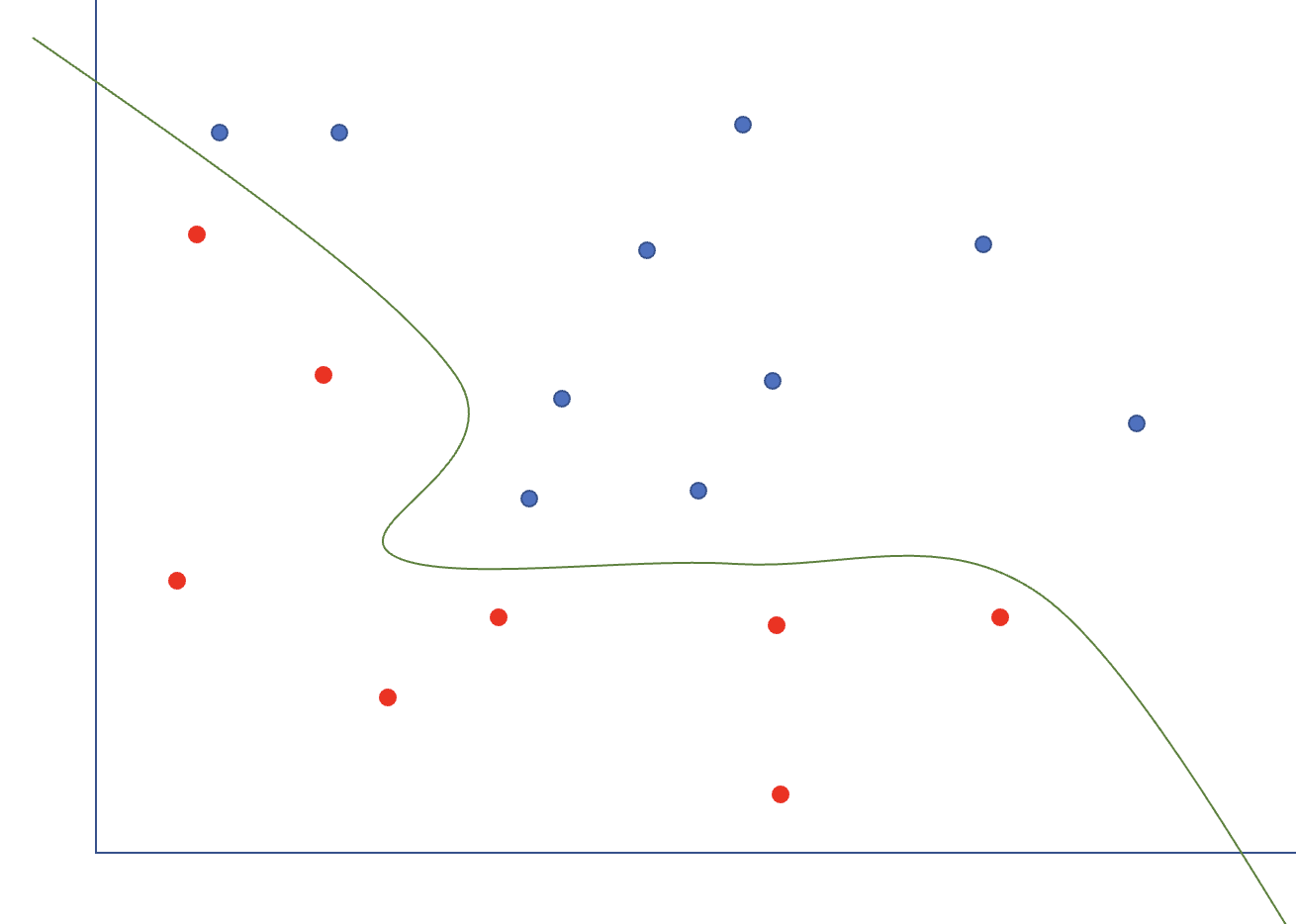
이전의 ML [5] Support Vector Machine(1)의 SVM은 에러가 있음을 인정하고 패널티를 주는 방식의 Linear의 형태지만 decision boundary를 complex하게 만들기 위해 모델을 complex하게 만들어 아래 그림 처럼 non-linear하게 만들 수 있다. 그때 필요한 것이 kernel trick이다.
Kernel Trick
- nonlinear하게 만드는 방법으로, x1,x2의 interaction을 더욱 복잡하게 표현하여(차원을 높여) 표현 할 수 있다.
- φ(<x1,x2>)=<x1,x2,x12,x22,x1x2,x13,x23,x12x2,x1x22>
- 이때 위 식 처럼 3차로 표현할 수 있는데, 무한대로 표현하면 더 잘 표현할 수 있을 것이고, 그때 필요한 것이 kernel trick이다.
Lagrange Method and Duality
: kernel을 도입하기 위해서 SVM의 primal 문제를 dual문제로 바꿔야하는데, 그때 사용하는 방법이 lagrange method이다.
- SVM은 classification문제를 constrained quadratic programming으로 바꾼다.
- Constrained optimization
- minxf(x)
- s.t. g(x)≤0,h(x)=0
- Lagrange method
- Lagrange Prime Function: L(x,α,β)=f(x)−αg(x)+βh(x)
- Lagrange Multiplier: α≥0,β
- Lagrange Dual Function: d(α,β)=infx∈XL(x,α,β)=minxL(x,α,β)
- maxα≥0,βL(x,α,β)=f(x):if x is feasible, ∞:otherwise
= minxf(x)→minxmaxα≥0,βL(x,α,β)
- Strong Duality
- primal solution와 dual solution이 같을때를 의미
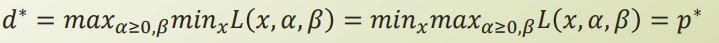
- 필요한 조건: KKT(Karush-Kunh-Trucker) condition
- KKT condition
- ∇L(x∗,α∗,β∗)=0
- α∗≥0
- g(x∗)≤0
- h(x∗)=0
- α∗g(x∗)=0
- SVM의 dual 표현:
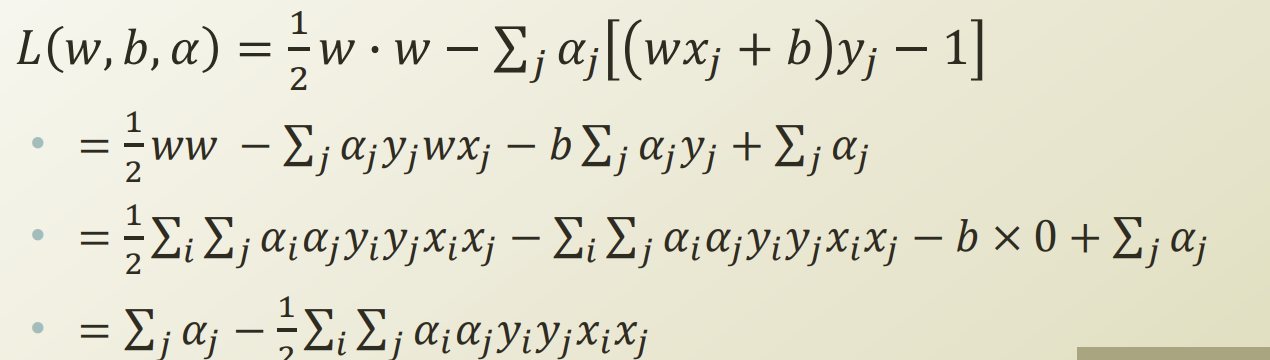
- 위의 표현은 또 다시 quadratic programming이 된다.
- 그렇다면 α만 안다면, w값을 구할 수 있게 된다.
Kernel
- Kernel: 두 벡터의 다른 공간에서의 inner product(내적)을 계산
- K(xi,xj)=φ(xi)φ(xj)
Dual SVM with Kernel Trick
- maxα≥0∑jαj−21∑i∑jαiαjyiyjφ(xi)φ(xj)
- => maxα≥0∑jαj−21∑i∑jαiαjyiyjK(xi,xj)
- αi((wxj+b)yj−1)=0,C>α>0
- w=∑i=1Nαiyiφ(xi)
- b=yj−∑i=1Nαiyiφ(xi)φ(xj)
- ∑i=1Nαiyi=0
- C≥αi≥0,∀i
- 따라서, 위의 식(kernel)을 통해서 classification할 수 있다