ML [6] Training/Testing and Regularization

본 포스팅은 카이스트 산업및시스템공학과 문일철 교수님의 Introduction to Artificial Intelligence/Machine Learning(https://aai.kaist.ac.kr/xe2/courses) 강의에 대한 학습 정리입니다.

이전 강의까지는 Machine learning 모델의 기능적인 면이 어느정도 완성되었음를 확인 할 수 있는데, 이러한 모델들이 그 기능을 "잘"하고 있는지 판단항 수 있는 지표가 필요하다.

• 확인해야할 요소:
  • 정확하게 추론 결과를 내는지
  • 정확도의 유효성
  • 테스트하는 데이터셋이 목적에 맞는지

Training and Testing

• Training
  • 파라미터를 인퍼런스하기 위한 과정
  • 사전 지식, 과거 경험을 통해
  • 도메인 정보가 바뀌거나 미래의 데이터가 분포가 바뀐다면, 재학습과정이 필요함
• Testing
  • 알고리즘과 추론 결과를 테스트
  • 학습과 관련 없는 데이터셋에 대해
  • 미래의 데이터셋

Overfitting and Under-fitting

: regrssion문제의 경우 아래와같이 판단된다.

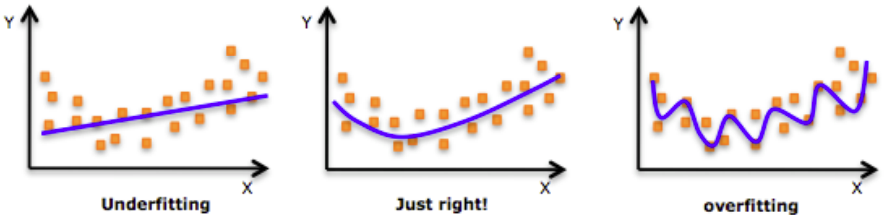
Tuning Model Complexity

: 모델이 복잡(N-degree)할수록 학습데이터를 과하게 train된다면 모델의 일반성을 잃게 되기 때문에 적당한 학습이 필요하다. 모델의 complexity와 generality는 trade-off.

ML에서의 Error

• Approximation과 Generalization에서의 두가지 source of error.
• $E_{out}\leq E_{in}+\Omega$
  • $E_{out}$: estiamtion error
  • $E_{in}$: approximation error
  • $\Omega$: 관찰의 다양성에 의한 error
• other symbols
  • f: target function
  • g: learning function of ML
  • $g^{(D)}$: learned functioon from Dataset
  • D: dataset
  • $\overline{g}=E_D[g^{(D)}(x)]$
• Vias and Variance
  
  • 위 식에서
    • $Varaince(x): E_D[(g^{(D)}-\overline{g}(x))^2]$
    • ${Bias}^2(x):(\overline g(x)-f(x))^2$
  • Variance는 제한된 데이터셋의 average hypothesis를 학습할때의 inability
    • more data로 보완
  • bias는 average hypothesis가 real world에 대한 inability
    • more model complexity로 보완
  • bias와 variance의 딜레마: trade-off

Performance Measurement

• Occam's Razor
  • competing hypotheses중 가장 적은 assumption을 가지는 것을 선택
  • competing: 예측에서 비슷한 에러를 가지는
  • fewest assumption: less complex model
• Cross Validaiton
  • 관찰 샘플은 유한하기 때문에,
  • 데이터셋을 N개로 나누고 (N-1)개를 학습에 1개를 testing에 사용(N-fold cross validation)
• 성능 측정 방법
  
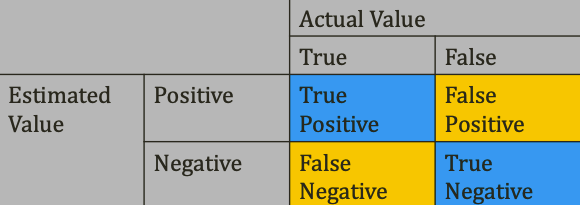
  • Accuracy: (TP+FN)/(TP+FP+FN+TN)
  • precision and recall: TP/(TP+FP), TP/(TP+FN)
  • F-Measure
    • F1: 2*(precision * reacall)/(precision + recall)
  • ROC curve

Regularization

• Regularization
  : variance로 부터 나온 error를 최소화, perfect fit 포기(=general, potential fit을 향상),
  • L1 regularization == Lasso regularization
    • The first order
  • L2 regularizatio
    • The second order