MeTRAbs Preprocess / Postprocess (전/후처리)

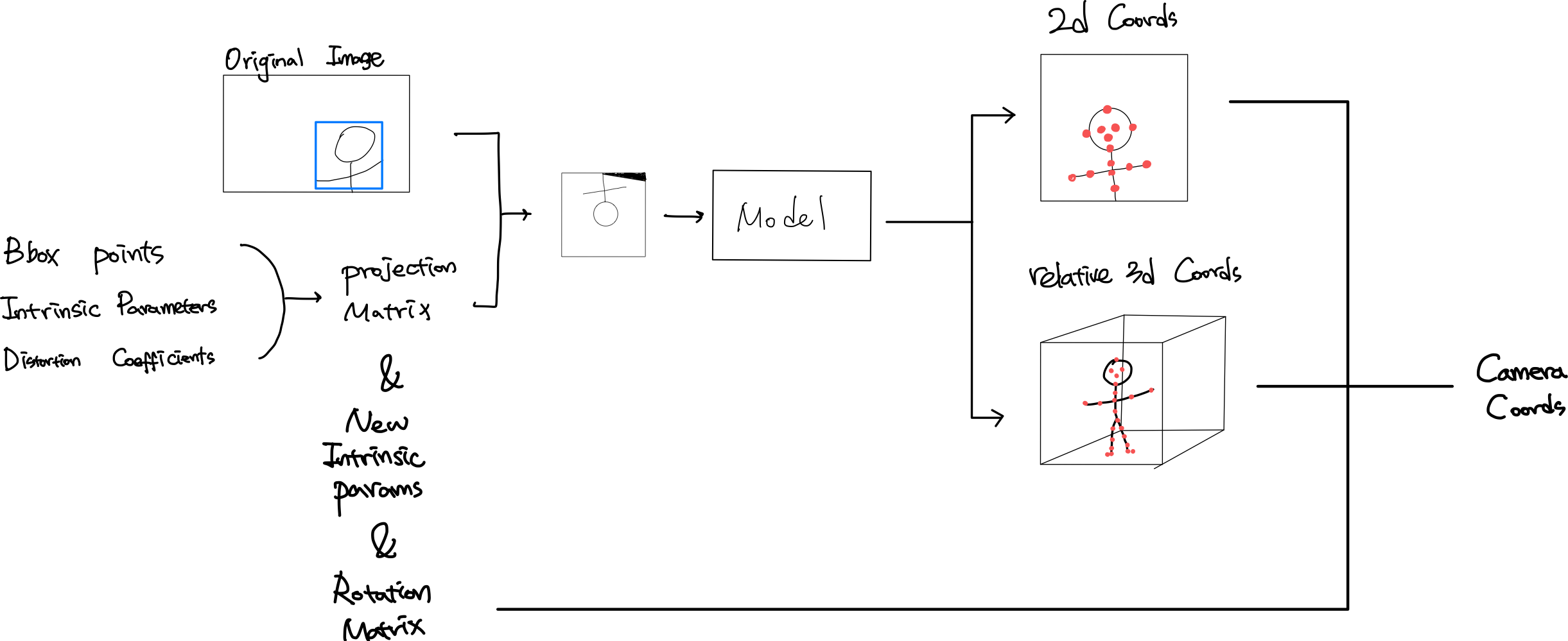
Pose Estimation 분야에는 최근 다양한 output 형태로 연구가 진행되고 있습니다. 여기서 말하는 output은 2D joint, 3D joint, mesh 등을 의미합니다. 아직까지 mesh형태를 출력하는 실시간 모델은 찾아보기 힘들고, 2D는 정확도도 높은 모델이 많고 가볍지만 활용도가 제한적이라는 생각입니다. 그래서, 3D joint를 추론하는 모델이 현 기술상 가장 활용도가 높지 않을까 생각합니다.

당연히 3D joint를 추론하는 방법도 한가지가 아닙니다. Voxel이라는 공간에 output을 제한시키는 경우도 있고, 카메라 좌표계나 새로운 좌표계상의 joint를 추론하는 방법 등 여러가지입니다. 물론, 초점을 어디두냐에 따라 모델 활용도가 무궁무진할 수 있죠. 많은 모델중에 지난번에 소개해드린 Metrabs는 2d좌표, voxel 공간상의 좌표, 카메라 좌표, 실제 world상의 좌표를 모두를 얻을 수 있는 모델인데요. 지금까지 이런 모델은 없었다. 이것은 사람이 추론한건가 모델이 추론한건가... 네..죄송합니다.🤪 그 정도로 정확도도 높고 많은 연구자들의 입맛에 맞출 수 있음을 강조하고 싶었습니다. 그 정도로 정확하고 활용도가 높습니다.

Metrabs의 특징으로는

• scale을 잘 고려된 3D 조인트를 잘 추론한다
  • 예를 들어, 두 이미지가 있다고 합시다. 한 이미지에는 한 사람의 몸 전체를 포함하지만, 다른 이미지에는 동일한 사람의 신체 일부(상반신, 하반신, 신체의 오른쪽 부분)만 포함되어 있을 때, 보통 3D pose estimation 모델은 두번째 이미지의 사람을 첫번째 이미지의 사람보다 훨씬 크게 추론할 겁니다. 하지만, Metrabs는 그 scale을 잘 고려한 추론 결과를 보여줍니다.
• 이미지 영역 밖의 보이지 않는 조인트에 대해서도 자연스러운 결과를 잘 추론한다.
  • 보통 pose 모델은 detector를 앞단에서 사용하여, 사람을 찾아내는데, 이때 신체 일부가 포함되지 못하는 경우가 가끔 일어납니다. 그럼 당연히 뒷단의 joint를 추론하는 모델에서는 없는 신체 일부에 대해서 부자연스러운 결과를 추론하는 경우가 많아요. 특히 heatmap을 활용하면 더 더욱 그럴 수 밖에 없습니다. 하지만, Metrabs는 자연스러운 포즈를 완성해줍니다.
• voxel좌표계, 카메라 좌표계, world 좌표 상의 모든 3D output을 얻을 수 있습니다.

위와 같은 특징을 가진 Metrabs는 사실 코드를 보면 조금 놀랍니다... 단순하지 않고 굉장히 많은 트릭들이 들어가 있어요. 그래서, 제가 Metrabs에 관해 두번째 포스팅을 하는 겁니다. 그럼 지금부터 제가 이해한 바를 설명해보겠습니다.

Metrabs Pose Model Input & Output

detector(yolo V4)를 제외한 Metrabs의 pose 모델만 보고, "아,resize해서 이미지를 넣어주면 되겠구나"하면 안됩니다!! 전체 이미지와 인물을 포함하는 bounding box 말고고, intrinsic parameter (카메라 내부 파라미터)와 distortion coeffiecients(왜곡 계수)가 필요합니다.

• Input
  • Resized Image
    • Projection Matrix (Intrinsic parameter + distortion + bbox)

그리고, output은 2d joint와 3d joint인데, 여기까지는 아직 완벽한 좌표를 얻을 수 없습니다. 심지어, 여기서의 3d coordinate은 카메라 좌표계도 아니고 그냥 voxel 공간상의 좌표(relative 3d coords)일 뿐입니다. 즉, 추가적인 후처리가 필요하다는 말이죠.

• Output (heatmap에 soft-argmax적용 후)
  • 2D Coords
  • Relative 3D Coords

Image PreProcess

먼저 어떤 프로세스인지 말씀드리자면, bbox의 중심과 네개의 모서리를 intrinsic parameter를 적용하여 camera space로 옮깁니다. 그 다음에, distortion 계수통해서 왜곡 보정된 bbox point구합니다. 그리고 이 point들을 다시 이미지로 옮기면서 새로운 intrinsic parameter를 구하죠. 동시에, camspace의 bbox의 중심에서 rotation matrix를 구하고 camera space상의 upvector를 통해서 projection matrix를 구합니다. 그럼 여기서, 구한 projection matrix 통해서 원본 이미지에 inverse된 projection matrix를 적용하고 다음은 distortion을 보정하고 다시 original intrinsic을 적용하여 변형된 이미지를 구할 수 있죠. 이렇게 변환된 이미지를 모델에 넣어줍니다. 변환 전과 변환 후의 이미지의 다름이 느껴지시나요?

이거 엄청 좋은 아이디어 아닌가요?! 다양한 카메라로 만들어진 데이터는 서로 다른 intrinsic이나 distortion이 있을텐데, 이 데이터들을 모두 동일한 기준에서 학습할 수 있다는 장점이 생기는거죠. 이건 웬만하게 카메라 calibration에 대해 이해하지 못하면 생각할 수 없는 트릭이라고 생각합니다.

• bbox 의 중심과 네개의 모서리 점을 inverse intrinsic을 적용하여 camspace상의 5개의 점 좌표를 구합니다.
• distortion coefficient를 통해 왜곡을 보정합니다.
  • 원본 이미지에서 머리가 살짝 타원형이지만, model input 이미지는 왜곡이 보정됨이 보이시나요?
• 보정된 center와 camera_space-up(up vector)를 통해, 새로운 좌표계를 만들고, 새 좌표계에 맞춘 rotation matrix를 구합니다.
  • 이미지가 거꾸로된 것과 오른쪽 윗 부분에 검은 부분이 들어간 것을 보시면, 조금 더 이해가 잘 되실 겁니다.
• 모서리 점들에 roation matrix와 intrinsic matrix를 적용하여 변환된 이미지상의 점들을 구하고, 이 점들로 이루어진 box의 크기를 구합니다.
• 새로 만들어진 box를 통해서, 새로운 nex intrinsic parameter를 구합니다.
• new intrinsic과 rotation matrix로 projection matrix를 구합니다.model input으로 들어갈 이미지를 만듭니다.

PostProcess

Metrabs 모델은 가장 첫번째로 2d heatmap(256256또는 384384)과 voxel 공간 (각 2.2m)상의 3d heatmap을 추론합니다. 다음은 soft argmax를 적용하여, 각 조인트(j)에 대한 2d 이미지상의 좌표 ($x_j,y_j$)와 3d 공간상의 좌표($\Delta X, \Delta Y, \Delta Z$) 이 과정은 워낙 많이 알려진 방법으로 따로 설명하지 않겠습니다. 단, 논문에서 나왔듯이 metrabs에서는 cetered stride를 사용합니다. 그래서 이미지 전체가 아닌 중심에서 일정 거리까지의 범위만 2D heatmap을 만들어줍니다. 때문에 아래 1번과 같은 처리를 해주는거죠.

Metrabs에서는 메인 아이디어는 다음과 같습니다. (논문 참고)
첫번째, 모델에 의해 구해진 voxel상의 좌표는 어떠한 기준 또는 offset만 있으면 카메라 좌표계상의 coordinate이라 할 수 있습니다.
두번째, image상의 좌표와 카메라 좌표를 normalized image plane으로 옮겨와 하나의 방정식을 만들죠.
그럼, 아래 이미지의 오른쪽 개념이 완성될 겁니다.

위의 수 많은 notation중에 우리가 모르는 것, 그리고 우리가 구해야하는 것은 $X_0, Y_0, Z_0$입니다. 이를 후처리에서는 LS square method를 통해서 구하죠.

자 그럼, 이제 Mrtabs의 메인 아이디어가 됐다면, 전체적인 후처리 과정을 살펴봅시다.

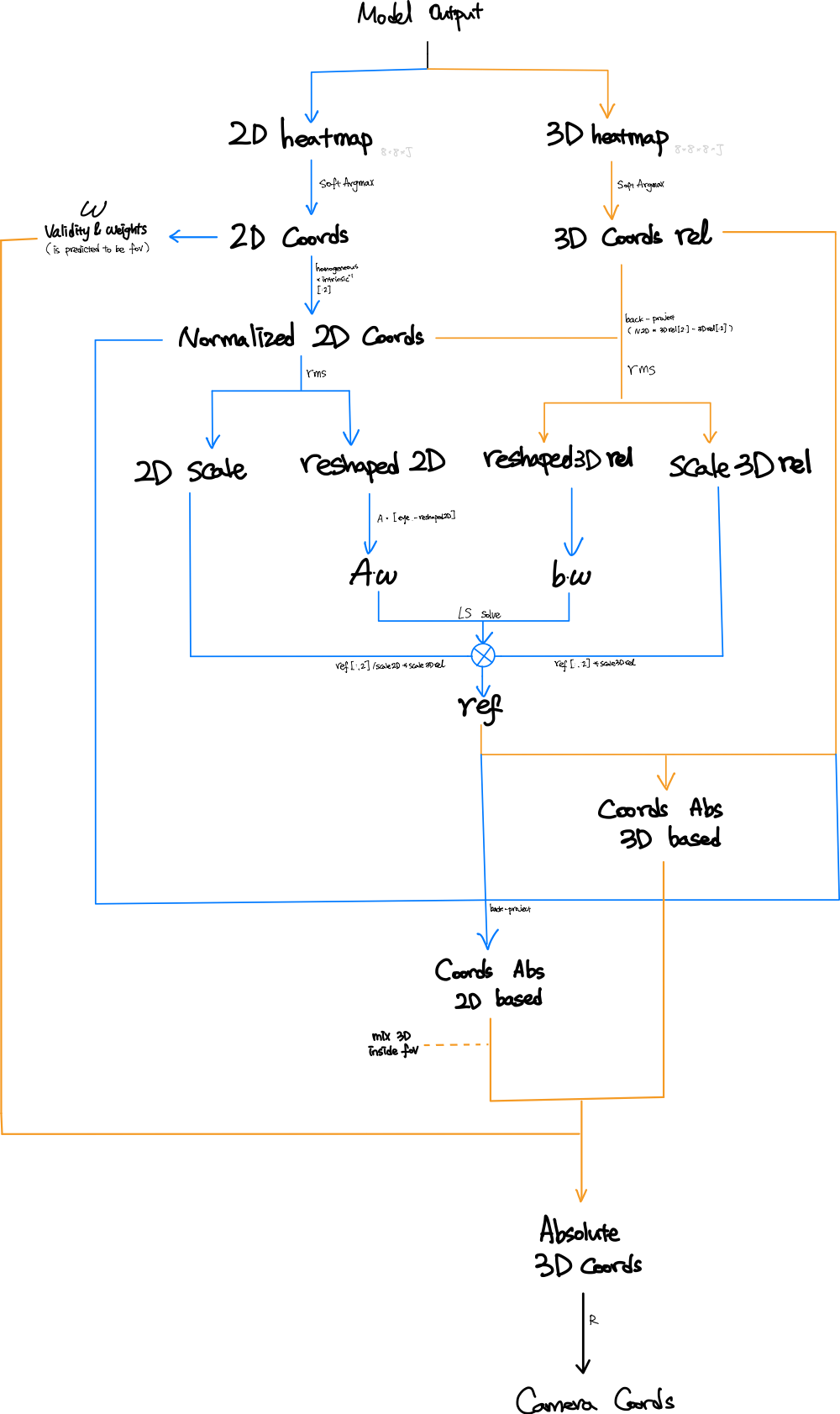
1. model input의 중심에서 일정 범위를 기준삼아, 그 안에 있는 joint에 대해서 1을, 그 밖의 joint들에 대해서 0을 weight로 계산합니다.

   def is_within_fov(imcoords, border_factor=0.75):
     stride_train = FLAGS.stride_train
     offset = -stride_train / 2 if not FLAGS.centered_stride else 0
     lower = tf.cast(stride_train * border_factor + offset, tf.float32)
     upper = tf.cast(FLAGS.proc_side - stride_train * border_factor + offset, tf.float32)
     proj_in_fov = tf.reduce_all(tf.logical_and(imcoords >= lower, imcoords <= upper), axis=-1)
     return proj_in_fov

2. 2d coords는 normalized image plane으로 옮기고, relative 3d coords는 project합니다.
   1) 이때, 2d는 (256,256) 3d는 voxel공간을 기준으로 있었기 때문에, scale이 다릅니다. 따라서 rms normalize를 적용하여 각각의 scale과 reshape된 좌표를 구합니다.

   def rms_normalize(x):
        scale = tf.sqrt(tf.reduce_mean(tf.square(x)))
        normalized = x / scale
        return scale, normalized

3. Metrabs의 메인 아이디어를 적용하여 방정식 $Ax = b$형태로 만듭니다.
   1) 주의할 점: 아까 구했던 wight를 적용하여, 유의미한 joint에 대해서만 연산될 수 있도록 합니다.
   2) $A=\begin{bmatrix} 1 & 0 & -\tilde{x_j} \\ 0&1&-\tilde{y_j} \end{bmatrix}, x=\begin{bmatrix}X_0 \\ Y_0 \\ Z_0 \end{bmatrix}, b=\begin{bmatrix}\tilde{x_j}\Delta Z_j-\Delta X_j \\\tilde y_j\Delta Z_j - \Delta Y_j\end{bmatrix}$
   3) 코드에서는 해를 ref(reference 값) 또는 offset이라고 지칭합니다.

4. LS 문제를 풀어 해를 구합니다.
   1) ref = tf.linalg.lstsq(A weights, b weights, l2_regularizer=1e-2, fast=True) 이용
   2) 구해진 ref에 scale값을 적용합니다.

   ref = tf.concat([ref[:, :2], ref[:, 2:] / scale2d], axis=1) * scale_rel_backproj 

5. 각각의 ouptut이였던 2d coord과 relative 3d coord로 3d 좌표를 구하고 적절히 더하여, absolute 3d cooord를 완성합니다.

    coords_abs_3d_based = coords3d_rel + tf.expand_dims(ref, 1)
    reference_depth = ref[:, 2]
    relative_depths = coords3d_rel[..., 2]

    coords_abs_2d_based = back_project(coords2d_normalized, relative_depths, reference_depth)
    
    coords_abs_2d_based = (0.5 * coords_abs_3d_based + (1 - 0.5) * coords_abs_2d_based)

    absoulute_3D = tf.where(is_predicted_to_be_in_fov[..., tf.newaxis], coords_abs_2d_based, coords_abs_3d_based)

6. 마지막으로 preprocess에 구한 Rotation matrix를 적용하여 camera coordinate을 구하고, 다시 project하고 distort를 적용하여 2d좌표를 구합니다. 마지막으로 extrinsic matrix를 적용하여 world coordinate를 구하고

여기까지가 Metrabs의 Post Prcess입니다. 저는 이걸 이해하면서 너무나 흥미로웠는데, 다른 분들은 어떠셨을지 궁금하네요 ㅎ

추가로!! 또 한번 더 놀랐던 점이 있었는데요.
초반의 Metrabs는 각 데이터셋의 annotation에 해당하는 모든 조인트를 다 각각 다른 점으로 추론했습니다. 그래서 output joint 개수가 555개나 되었죠.
하지만 최신 업데이트된 모델은 output이 32개인데요. 이 아이디어는 지난 포스팅 중에 여러가지 데이터셋을 임베딩 벡터로 표현하는 방법이 도입된 것입니다. 한번 읽어보시길 추천합니다.
결과적으로, 32개의 임베딩 벡터로 아웃풋을 바꾸고, 미리 학습되었던 decoder를 붙여 원하는 데이터셋의 조인트를 얻어냅니다. 이렇게 하면 학습에도 더 좋은 효과가 있었겠죠?

정말 여러번 감탄하면서 읽고 테스트해본 논문인데, 제가 잘 표현했을지 모르겠습니다....😅
저는 그럼 또 다른 포스팅으로...