[알고리즘] BFS & DFS

BFS와 DFS는 기본적으로 그래프를 탐색하는 알고리즘입니다.

그래프(Graph)는 노드(Node)와 간선(Edge)으로 구성되어 있는 자료 구조입니다. 노드는 그래프의 정점을 나타내고, 간선은 정점들을 연결하는 선입니다.

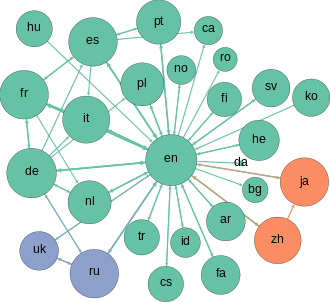
노드(Node)는 그래프의 정점을 나타냅니다. 각 노드는 고유한 식별자를 가지며, 데이터나 추가 정보를 포함할 수 있습니다.

간선(Edge)은 그래프의 노드들을 연결하는 선입니다. 간선은 노드 사이의 관계나 연결을 나타내며, 방향성과 가중치를 가질 수 있습니다.

* BFS, DFS의 정의

1. BFS(Breadth First Search, 너비 우선 탐색)는 시작 노드에서 인접한 노드를 우선적으로 방문하고, 그 다음에 해당 인접 노드들의 인접 노드들을 방문하는 방식으로 탐색을 진행합니다. 즉, 노드들을 너비(레벨)별로 탐색합니다. BFS는 큐(Queue) 자료구조를 사용하여 구현되며, 최단 경로를 찾는 데에 유용합니다.

2. DFS(Depth First Search, 깊이 우선 탐색)는 시작 노드에서부터 최대한 깊이 진행하면서 더 이상 진행할 수 없을 때까지 탐색을 진행한 후, 되돌아와 다음 인접 노드를 탐색하는 방식으로 진행됩니다. 즉, 한 경로를 따라 끝까지 탐색한 후, 되돌아와 다른 경로를 탐색합니다. DFS는 스택(Stack) 자료구조를 사용하여 구현됩니다.


BFS와 DFS의 차이점을 표로 정리하면 다음과 같습니다.

번호	항목	BFS	DFS
1.	정의	한 레벨의 모든 노드를 탐색한 후 다음 레벨로 이동하는 탐색 방식	루트 노드에서 시작하여 임의의 브랜치(서브 트리)의 모든 노드를 탐색할 때까지 가능한 깊이 탐색하는 방식
2.	사용 자료 구조	큐(Queue) -> FIFO(First-in, First-out)	스택(Stack) -> LIFO(Last-in, First-out)
3.	탐색 기법	루트 노드에서 목표 노드까지 최단 경로를 탐색	루트 노드에서 목표 노드까지 가능한 모든 경로를 탐색
4.	트리 구조	트리의 노드를 레벨별로 구축	트리를 루트 노드에 가까운 노드들을 기준으로 브랜치(서브 트리)로 구분
5.	적합성	목표 노드가 가깝고 탐색 데이터가 작음	목표 노드가 멀고 탐색 데이터가 클 때
6.	메모리 용량	큼	작음(상대적)
7.	무한 루프 가능성	X	O(순환형 그래프 탐색 시)
8.	시간 복잡도	$O(V + E)$	$O(V + E)$
9.	속도	느림	빠름 (메모리 용량 차이로 인해 일반적으로 빠르지만, 상황에 따라 다를 수 있음)

그래프를 통해 BFS와 DFS의 작동 방식을 알아보겠습니다.

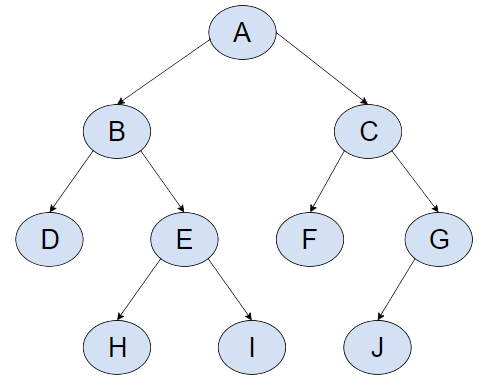
• BFS : A(Root) → (B → C : level 1) → (D → E →F → G: level 2) → (H → I → J level 3)
  루트 노드부터 한 층씩 내려가며 일정한 방향으로 노드를 탐색합니다.
  
  
• DFS : A(Root) → (B → D) → (E → H → I) → (C → F) → (G → I)
  우선 루트에서 가장 왼쪽의 브랜치(A → B → D)를 탐색합니다. 더 이상 탐색할 미방문 노드가 없으므로 노드를 역행하며(D → A) 미방문 자식 노드가 있는 노드(B)를 찾으면 다시 탐색을 시작합니다(B → E). 왼쪽 브랜치의 모든 노드를 탐색하면 A로 돌아가 같은 방법으로 오른쪽 브랜치를 탐색합니다.

다음은 위의 그래프를 BFS, DFS로 탐색하는 과정을 파이썬 코드로 구현한 예시입니다.

graph = {
    'A': ['B', 'C'],
    'B': ['A', 'D', 'E'],
    'C': ['A', 'F', 'G'],
    'D': ['B'],
    'E': ['B', 'H', 'I'],
    'F': ['C'],
    'G': ['C', 'J'],
    'H': ['E'],
    'I': ['E'],
    'J': ['G']
}


# BFS
from collections import deque

def bfs(graph, start):
    visited = set()  # 방문한 노드를 저장하는 집합
    queue = deque([start])  # 방문할 노드를 저장할 큐

    while queue:
        node = queue.popleft()  # 큐에서 노드를 꺼냄

        if node not in visited: # 노드를 방문하지 않았다면
            print(node, end=' ')  # 노드 출력
            visited.add(node)  # 방문 처리

            # 인접 노드 중 방문하지 않은 노드 탐색
            for neighbor in graph[node]:
                if neighbor not in visited:
                    queue.append(neighbor)

# DFS
def dfs(graph, start):
    visited = set()  # 방문한 노드를 저장하는 집합
    stack = [start]  # 방문할 노드를 저장할 스택

    while stack:
        node = stack.pop()  # 스택에서 노드를 꺼냄

        if node not in visited: # 미방문 노드를
            print(node, end=' ')  # 출력
            visited.add(node)  # 방문 처리

            # 방문하지 않은 노드를 스택에 추가
            for neighbor in graph[node]:
                if neighbor not in visited:
                    stack.append(neighbor)
                    
                    
# BFS, DFS 호출
bfs(graph, 'A' )
print()
dfs(graph, 'A')

  	(Output)  
A B C D E F G H I J 
A C G J F B E I H D 

DFS의 경우 stack에서 pop하다 보니 B, C중에서 C를 pop하므로 위와 달리 가장 오른쪽 브랜치부터 탐색을 합니다. 따라서 순서에 차이가 있지만 여전히 BFS와 DFS의 탐색 순서를 확인할 수 있습니다.