[Design Principle] Liskov Substitution Principle

정의

What is wanted here is something like the following substitution property: If
for each object o1 of type S there is an object o2 of type T such that for all
programs P defined in terms of T, the behavior of P is unchanged when o1 is
substituted for o2 then S is a subtype of T.

"각각의 S타입의 object o1에 대해, T타입의 object o2가 존재하고, T에 대해 정의된 모든 프로그램 P에서 o1이 o2로 치환될 때, P의 동작이 변하지 않으면 S는 T의 subtype이다."가 Liskov substitution principle(이하 LSP)의 정의입니다. 이를 간단히 요약해보면 아래와 같습니다.

Subtypes must be substitutable for thier base types.

"Subtype은 자신의 base type에 치환 가능해야 한다."가 간단히 요약한 LSP의 정의입니다.

Rectangle과 Square

LSP의 유명한 예제로 Rectangle과 Square 예제가 있습니다.
정사각형은 직사각형의 특수한 형태로 모든 변의 길이가 같은 정사각형입니다. 그러므로 정사각형과 직사각형을 나타내는 클래스를 생성할 때 아래와 같이 Square 클래스가 Rectangle 클래스를 상속받도록 정의할 수 있습니다.

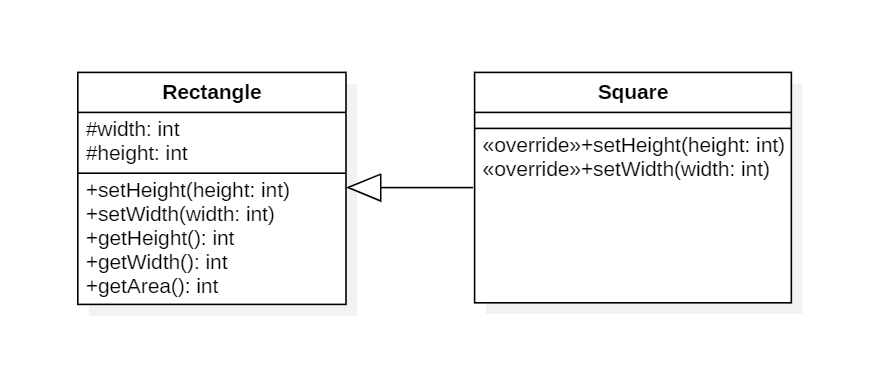
정사각형은 높이와 밑변의 길이가 항상 같으므로 Rectangle의 setHeight와 setWidth를 override하여 width와 height가 동시에 변경되도록 정의하면 다음과 같습니다.

class Square extends Rectangle {
    public Square(int side) {
        super(side, side);
    }

    @Override
    public void setHeight(int height) {
        super.setHeight(height);
        super.setWidth(height);
    }

    @Override
    public void setWidth(int width) {
        super.setWidth(width);
        super.setHeight(width);
    }
}

아직까진 별 문제가 없어보입니다. 하지만 아래와 같이 Rectangle 클래스를 parameter로 받아 사용하는 클래스가 있다고 가정해봅시다.

class RectangleConsumer {
    public void assertArea(Rectangle r) {
        r.setWidth(5);
        r.setHeight(2);
        
        assertThat(r.getArea(), is(10)); // assertion error when r is Square
    }
}

assertArea에 Rectangle object를 넘겨주면 아무런 문제가 없지만 Square object를 넘겨주면 width와 height가 동시에 변경되므로 r.getArea()를 호출하면 4를 return하여 문제가 발생하게 됩니다. 그러므로 Rectangle은 자신의 subtype인 Square로 치환이 불가능하며 Square는 적절한 subtype이 아닙니다.

그러면 LSP를 만족하기 위해서는 어떤 것들을 지켜야 하는지 알아보겠습니다.

Supertype의 method 동작 보존

Subtype($\sigma$)은 자신의 supertype($\tau$)의 method 동작을 보존해야 합니다. Supertype의 method를 $m_{\tau}$라 하고 이에 해당하는 subtype의 method를 $m_{\sigma}$라 하겠습니다.

Signature Rule

Contravariance of Arguments

$m_{\tau}$ and $m_{\sigma}$ have the same number of arguments. If the list of argument types of $m_{\tau}$ is $a_{i}$ and that of $m_{\sigma}$ is $\beta_{i}$, then $\forall i$. $\alpha_{i} \preceq \beta_{i}$.

$m_{\tau}$와 $m_{\sigma}$는 같은 수의 argument를 가지고 $m_{\sigma}$의 argument들은 $m_{\tau}$의 argument들의 supertype이거나 같은 type이어야 합니다.

위와 같이 argument type이 정의되어 있고 $m_{\tau}$가 Argument를 받을 때, $m_{\sigma}$에서 $m_{\tau}$로 받은 Argument를 SuperArgument로 처리는 가능하지만 SubArgument로의 처리는 불가능한 경우가 존재합니다. 그러므로 프로그램의 동작을 보장할 수 없게 됩니다.

Covariance of Result

Either both $m_{\tau}$ and $m_{\sigma}$ have a result or neither has. If there is a result, let $m_{\tau}$'s result type be a $\alpha$ and $m_{\sigma}$'s be $\beta$. Then $\beta \preceq \alpha$.

$m_{\tau}$와 $m_{\sigma}$ 둘 다 결과를 가지지 않거나 둘 다 결과를 가져야 합니다. 만약 결과를 가지면 $m_{\sigma}$의 결과는 $m_{\tau}$의 결과의 subtype이거나 같은 type이어야 합니다.

이는 contravariance of arguments와 마찬가지로 $m_{\sigma}$이 SubResult를 return하면 Result로 처리가 가능하나 SuperResult는 처리할 수 없는 경우가 존재합니다.

Exception Rule

The exceptions signaled by $m_{\sigma}$ are contained in the set of exceptions signaled by $m_{\tau}$.

$m_{\sigma}$에서 발생하는 exception들은 $m_{\tau}$에서 발생하는 exception들에 속해야 합니다. 즉, $m_{\tau}$에서 발생하지 않는 exception을 $m_{\sigma}$에서 throw해서는 안됩니다.
Client는 $m_{\tau}$에서 발생하는 exception들은 예상하여 처리할 수 있지만 그 외의 exception이 발생하게 될 경우 exception을 적절히 처리할 수 없어 프로그램의 동작을 보장할 수 없게됩니다.

Methods Rule

• Pre-condition
  코드를 실행하기 전에 만족해야하는 조건입니다. 만약 pre-condition을 만족하지 못했을 경우, 코드의 올바른 동작을 보장할 수 없습니다.

• Post-condition
  코드를 실행 후 만족해야하는 조건입니다. 코드의 동작과 정상적인 값을 return하는지 보장해야합니다.

Pre-condition Rule

$m_{\tau}.pre[A(x_{pre})/x_{pre}] \Rightarrow m_{\sigma}.pre$

$m_{\sigma}$의 pre-condition은 $m_{\tau}$의 pre-condition보다 강해져서는 안됩니다. 만약 이를 어기게 되면 client는 $m_{\tau}$의 pre-condition을 예상하고 코드를 작성하게 되는데 $m_{\sigma}$의 pre-condition이 더 강해지면 원래는 정상 동작해야할 코드가 제대로 동작하지 않는 경우가 발생하게 됩니다.

Post-condition Rule

$m_{\sigma}.post \Rightarrow m_{\tau}.post[A(x_{pre})/x_{pre}, A(x_{post})/x_{post}]$

$m_{\sigma}$의 post-condition은 $m_{\tau}$의 post-condition보다 약해져서는 안됩니다. 만약 $m_{\sigma}$가 더 약해질 경우 예상치 못한 return 값을 받아 client에서 처리하게 되는 경우가 발생합니다. 이렇게 예상치 못한 return 값을 받을 경우 client에서 해당 값을 어떻게 처리해야할지 모르므로 제대로된 동작을 보장할 수 없습니다.

Supertype의 property 보존

Subtype은 supertype의 property를 보존해야 하며 해당 property는 아래와 같습니다.

• Invariant
  Object의 life time동안 계속 만족해야하는 제약사항입니다. Invariant는 주로 software object가 정의되고 나서 해당 object가 현실에서 적용되는 rule을 나타냅니다.

• Constraint
  Object-oriented model 혹은 system의 제약사항입니다. Constraint는 클래스 레벨에서 정의되어 있지만 적용은 object 레벨에서 이루어집니다.

Invariant Rule

Subtype invariants ensure supertype invariants
$I_{\sigma} \Rightarrow I_{\tau}[A(x_{\rho})/x_{\rho}]$

Subtype의 invariant는 supertype의 invariant를 보장해야합니다.

Constraint Rule

Subtype constraints ensure supertype constraints
$C_{\sigma} \Rightarrow C_{\tau}[A(x_{\rho})/x_{\rho}, A(x_{\psi})/x_{\psi}]$

Subtype의 constraint는 supertype의 constraint를 보장해야합니다.

Rectangle과 Square의 문제점

위의 Rectangle과 Square의 예제에서 Square는 Rectangle의 적절한 subtype이 아님을 알았습니다. 그러면 Square에서 어떤점 때문에 문제가 발생했을까요? 그 이유는 Square의 method가 Rectangle의 method보다 post-condition이 더 약하기 때문입니다.

Rectangle의 setWidth의 post-condition은 코드에서 명시하지는 않았지만 아래와 같습니다.

// old is the value of the Rectangle before SetWidth is called.
assert((this.width == width) && (this.height == old.height)); 

하지만 Square의 setWidth에서는 height가 width와 동시에 변하므로 Rectangle의 setWidth의 post-condition 중 this.height == old.height가 지켜지지 않는 것을 볼 수 있습니다. 그러므로 Square의 setWidth의 post-condition은 Rectangle의 setWidth의 post-condition보다 약하고 그로 인하여 LSP를 위배하게 된 것입니다.

Reference

[1] Barbara H. Liskov, Jeannette M. Wing, Behavioral Subtyping Using Invariants and Constraints (n.p.: n.d, 1999), 10.

[2] Robert Martin, Agile software development: principles, patterns, and practices (n.p.: Pearson, 2013), 111-125.

[3] Robert Martin, Clean Architecture: A Craftsman’s Guide to Software Structure and Design (n.p.: Prentice Hall, 2017), 78-82.