[Week 0] Convex Optimization :: Introduction

Intro

이번 방학 세션에서 다룰 주제는 '최적화 이론'이다.

사실 최적화라는 것은 낯선 것이 아니다. 왜냐하면 우리 주변의 모든 의사 결정 문제를 최적화 문제라고 할 수 있기 때문이다. 가령 '오늘 밤 몇 시에 잠자리에 들지'를 결정한다는 것은 하루라는 제한된 시간 내에, 오늘 할 일을 많이 해서 얻는 편익과 내일의 피곤 사이의 손익을 따져 합리적인 결정, 즉 최적의 결정을 내리는 것이다.

그렇지만 우리는 이들 중 수학적으로 객관적인 답을 도출할 수 있는 문제에만 관심을 둘 것이다. 즉 '최적의 의사 결정'이라는 추상적인 개념을 객관적인 수치로 표현하여 모두가 납득할 수 있어야 한다. 이를 수식으로 표현하면 아래와 같다.

$\text{minimize}\,\,f_0 (x)$
$\text{subject to}\,\,f_i (x)≤b_i,\,i=1,2…,m$

• $x= (x_1, ..., x_n)$ ; Optimization Variable
• $f_0 : R^n →R$ ; Objective Function
• $f_i : R^n →R, i=1,...,m$ ; (Inequality) Constraint Functions
• $b_i$ : Bounds of constraint functions

최적의 의사 결정은 일반적으로 편익을 최대화 또는 비용을 최소화하는 문제로 수치화할 수 있다. 둘은 서로 뒤집으면 결국 같은 말이 될 때가 대부분이다. 위에서 우리가 문제를 푸는 대상은 $f_0(x)$로, $\mathbb{R}^n$상의 벡터 $x$에 대해 스칼라 값으로 나타나는 함수이다. 이 함수가 최소 또는 최대의 값을 가지게 되는 $x$를 찾는 것이 최적화 문제의 목표이다.
하지만 실제 문제를 풀 때는 여기에 추가적인 제약식을 고려할 필요가 있다. optimization variable은 자원의 투입량을 나타낼 때가 많은데, 현실적으로 자원을 무한정 투입할 수 없기 때문이다. 제약식은 일반적으로 위와 같은 부등식 형태로 나타난다.

따라서 최적화 문제의 해 ($x^*$ ; Optimum / Solution of the problem)는 모든 $z \in \text{dom}f_i$에 대하여 $f_1(z) \leq b_1,\,f_2(z) \leq b_2,\, ...\,,\,f_m(z) \leq b_m,\,f_0(z) \geq f_0(x^*)$ 의 관계식을 만족하게 된다.

Convex Optimization

이번 학기 세션에서는 Convex Optimization에 대해 중점적으로 다룰 것이다. Convex Optimization problem은 objective와 constraint function이 convex한 경우를 다루는 최적화 문제이다. Convex한 경우에 대해 우선적으로 다루는 이유는 한 마디로 비교적 쉽기 때문이다.

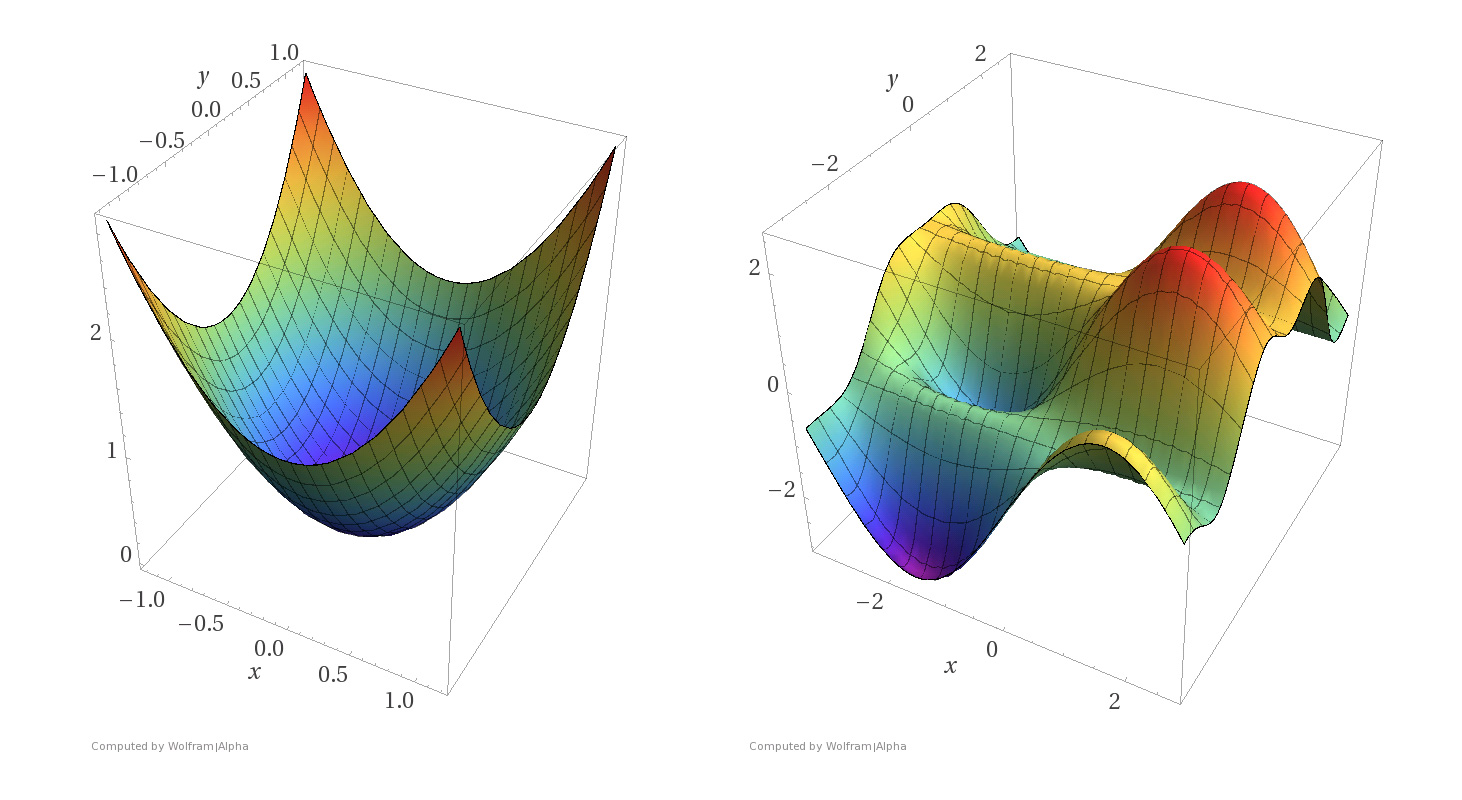
Convex function의 수학적인 정의는 앞으로 배우겠지만, 직관적으로 우선 보면 이런 종류의 함수의 값(스칼라장)은 위 그림의 왼쪽처럼 오목한 형태로 되어 있다. 이런 함수는 눈으로 봐도 쉽게 알 수 있듯, 모든 $x$에 대한 최소 지점, 즉 global minimum을 비교적 쉽게 찾을 수 있을 뿐 아니라 알고리즘을 통해 다항 시간 내에 global minimum을 찾을 수 있음이 보장되어 있다. 반면 오른쪽처럼 non-convex한 형태의 경우 많은 알고리즘이 global minimum으로 수렴함을 보장하지 못하고, 주변에서만 가장 작은 지점인 local minimum만 찾을 수 있을 가능성이 높고 다항 시간 내에 알고리즘으로 풀 수 없는 NP-hard 문제일 가능성도 있다. 따라서 non-convex에 대해 다루는 것은 훨씬 복잡한 문제이기 때문에, 우선 우리는 convex한 경우에 대해 다룰 것이다.

convex optimization 문제를 수식으로 표현하면 다음과 같다.

$\text{minimize}\,\,f_0(x)$
$\text{subject to}\,\, f_i(x) \leq b_i,\,i=1,2,...,m$
Objective and constraint functions are convex, i.e.,
$f(\theta x+(1-\theta)y) ≤ \theta f(x)+(1-\theta)f(y)\,\,\text{for}\,\,0 \leq \theta \leq 1$

예시를 통해 문제 상황을 어떻게 컨벡스 최적화 문제로 표현할 수 있는지 살펴보자.

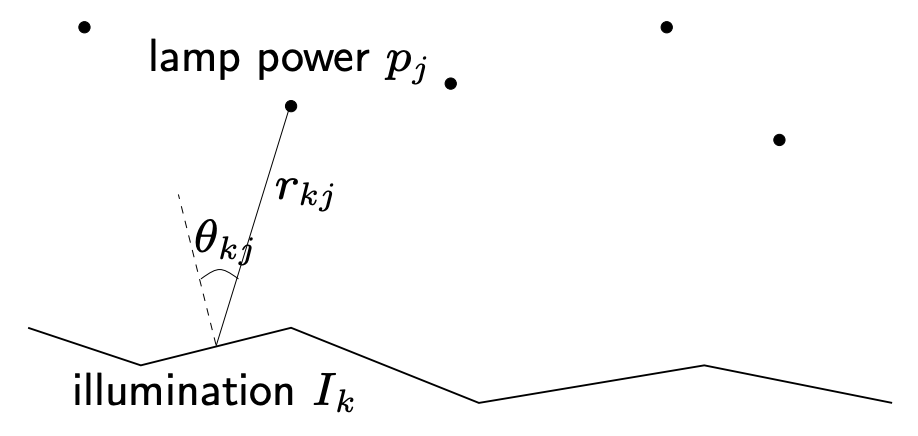
(Example-lamp illuminating problem)

• Situation: n개의 구역을 밝히고 있는 m개의 불빛이 있을 때, $k$번째 구역의 밝기 $I_k$는 불빛에 할당된 전력 $p_j$에 의존한다.
  $I_k = \displaystyle\sum_{j=1} ^{m} a_{kj}p_j,\,\,a_{kj}=r_{kj}^{-2}max\{cos\theta _{kj}, 0\}$
• Problem: 제한된 전력량 내에서 각 구역의 원하는 밝기 $I_{des}$를 최대한 가깝게 달성하자. 이 문제는 수식으로 다음과 같이 나타낼 수 있다.
  $\text{minimize}\,\,\max_{k=1,2,...,n} |logI_k-logI_{des}|$
  $\text{subject to}\,\,0 \leq p_j \leq p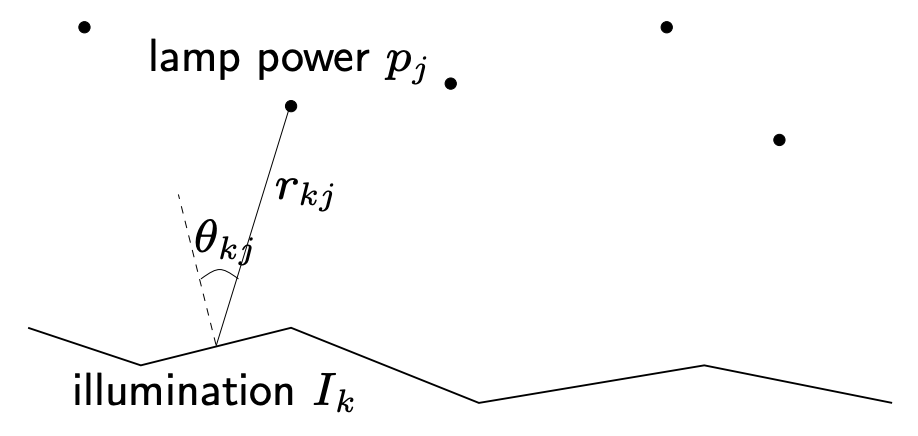_{max},\,\,j=1,...,m$

이 문제 상황에 대해 다음과 같이 다양한 해결법들을 적용할 수 있다.

(1) Uniform Power $p$ ; $p_j = p$

(2) Least squares ; $\text{minimize} \displaystyle\sum_{k=1} ^{n}(I_k-I_{des})^2$, $\text{round if}\,\,p_j > p_{max}\,\,\text{or}\,\,p_j <0$

(3) Weighted least squares ; $\text{minimize} \displaystyle\sum_{k=1} ^{n}(I_k-I_{des})^2+\displaystyle\sum_{j=1} ^{m}w_j(p_j-p_{max}/2)^2$, $0 \leq p_j \leq p_{max}$가 될 때까지 반복

(4) Linear programming; $\text{minimize}\,\,\max_{k=1,2,...,n}|I_k-I_{des}|$, $\text{subject to}\,\, 0 \leq p_j \leq p_{max},\,\, j=1,2,...,m$

(5) Convex Optimization ; $\text{minimize}\,\, f_0(p)=max_{k=1,2,...,n}h(I_k/I_{des})$, $\text{subject to}\,\, 0 \leq p_j \leq p_{max},\,\,j=1,2,...,m$
$\text{where}\,\,h(u) = \max\left\{u, 1/u \right\}$

결국 가장 어려운 요소는 문제 상황이 컨벡스 최적화로 해결될 수 있는 상황임을 인지하고, 적절히 표현하는 것이다. 또, 얼핏 non-convex처럼 보이는 상황이더라도 몇몇 trick을 이용해 convex로 변환해 근사적인 최적값을 구할 수도 있다.

앞으로의 세션에서 컨벡스 최적화의 수학적 성질들에 대해 자세히 살펴보면서 최적화와 함께 놀아 보자😆