[Week 1] Convex sets [1]

*세션 교재: Convex Optimization – Boyd and Vandenberghe. Ch.1.

1주차 세션은 Convex set에 관해 다룬다. 컨벡스 최적화 문제의 성립 조건 중, problem domain이 convex set일 것이 있다. 따라서 이번 세션에서는 convex set의 성질과 다양한 convex set을 살펴볼 것이다.

1. Affine sets and convex sets

Affine sets

$\mathbb{R}^n$상의 벡터 $x_1,\,x_2,\,...,\,x_n$을 선형 결합할 때, 선형 결합의 계수 $\theta_1,\,\theta_2,\,...,\theta_n$에 대한 세 가지 서로 다른 조건을 살펴보자.

$1.\, \theta_1 + \cdots + \theta_n = 1$
$2.\, \theta_1 + \cdots + \theta_n = 1,\,\,\theta \succeq 0$
$3.\, \theta \succeq 0$

먼저 1번과 같은 조건의 선형 결합을 아핀 결합(affine combination)이라고 한다. 이것의 가장 간단한 예시는 두 점을 잇는 직선상의 점이다. 이것을 일반화해 어떤 집합이 아핀 결합에 대해 닫혀 있으면, 즉 그 집합의 임의의 원소들에 대한 아핀 결합도 그 집합에 속한다면 이 집합을 affine set이라고 한다. 그리고 affine hull $\text{aff}\,C$은 임의의 집합 $C$의 원소들을 모두 포함하는 가장 작은 affine set이다.

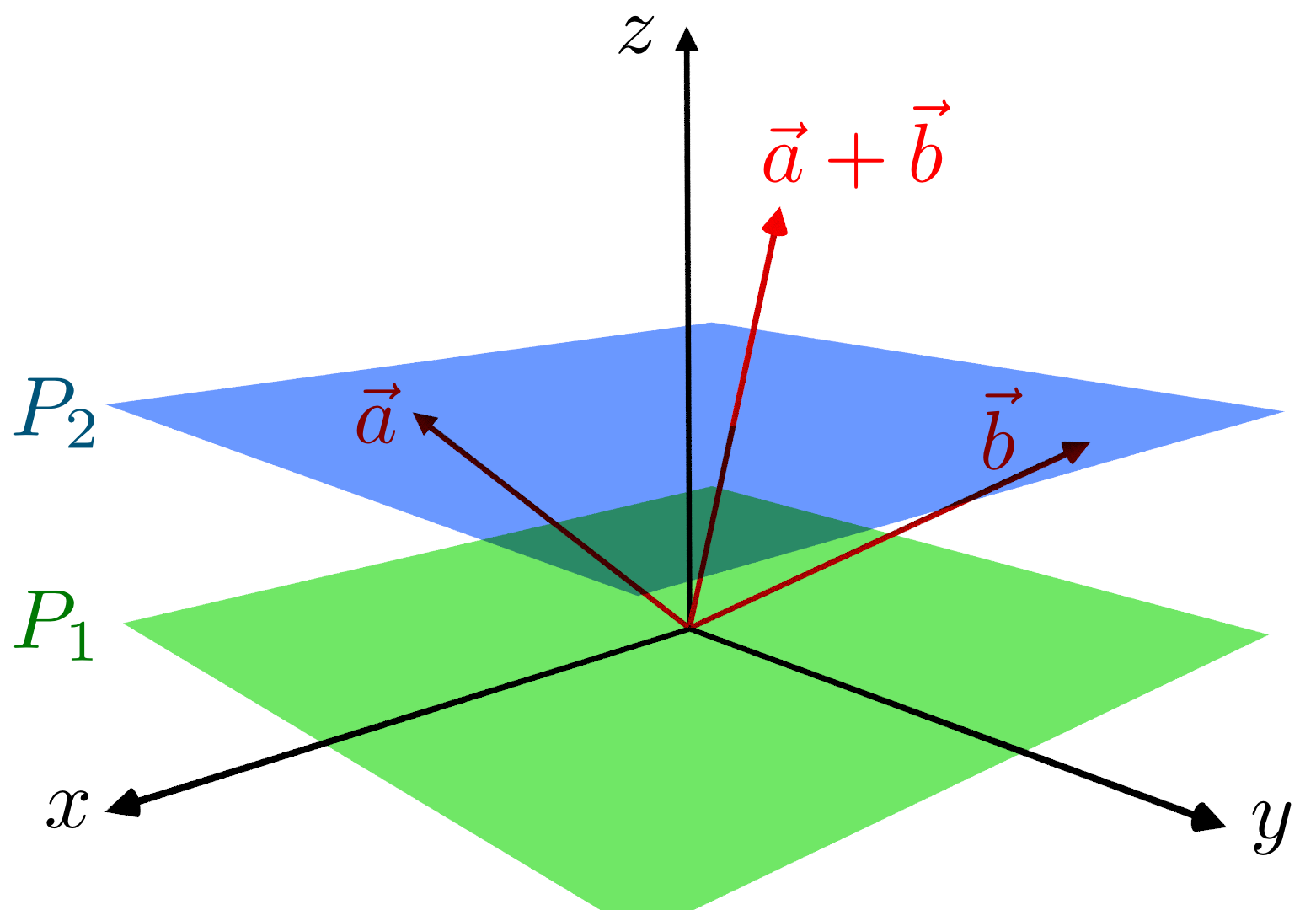
Affine set은 평행이동된 subspace로 해석될 수 있다. Subspace와는 달리 일반적으로는 원점을 포함하지 않기 때문에 덧셈에 대해 닫혀 있지 않다. 만약 affine set을 어떤 대수적인 공간으로 본다면 원점이 정의되어 있지 않으므로 그 안에서 벡터의 크기와 각도를 논하는 것은 의미가 없다. 그렇지만 affine set 상의 두 벡터의 위치를 서로 빼서 방향은 정의할 수 있다. 즉 affine space는 본래 원점이 없는, 즉 점들 사이의 상대적인 위치와 방향만 정의된 공간인데, 만약 여기에서 원점 $(0,0)$을 정한다면 vector space가 정의되므로 affine space는 vector space를 평행이동시킨 동일한 모양의 공간이라고 이해될 수 있다. 따라서 아래의 예제와 같이 homogeneous하지 않은 경우를 포함한 일반적인 linear system의 solution space로 해석될 수 있다.

Affine dimension and relative interior

집합 $C$의 affine hull의 차원을 affine dimension 으로 정의한다.

$C\subseteq R^n$의 affine dimension이 n보다 작을 경우, 집합 $C$의 relative interior $\text{relint}\,C$를 아래와 같이 정의한다.

$B$$(x,r)$은 반지름이 $r$이고 중심이 $x$인 구를 말한다.
$C$의 경계를 $\text{cl}\,C$ 라 하며, relative boundary를 $\text{cl}\,C \backslash \text{relint}\,C$로 정의한다.

이것이 무슨 의미인지 파악해 보자. 우선 interior의 정의는 다음과 같다.

위상공간 $X$의 부분집합 $S$에 대해, $S$의 부분집합 중 모든 열린 집합의 합집합

유클리드 공간 상에서는 아래와 같이 정의할 수 있다.

If $S$ is a subset of a Euclidean space, then $x$ is an interior point of $S$ if there exists an open ball centered at $x$ which is completely contained in $S$

가령 $(0,0)$과 $(1,1)$을 잇는 line segment가 있다고 할 때, 이 집합의 interior는 empty set이다. line segment 안의 점 하나를 선택해 위상공간 $\mathbb{R}^2$ 기준으로 open ball인 매우 작은 원을 그렸을 때, line segment를 벗어나기 때문이다.

반면 relative interior는 affine hull을 기준으로 정의된다. 즉 어떤 set을 그 set이 span하는 affine space의 subset이라는 관점으로, interior가 정의되는 전체 위상공간을 유클리드 공간 $\mathbb{R}^n$에서 affine space로 축소한 것이다. 그래서 open ball과 affine hull의 교집합을 이용해 정의하는 것이다. 따라서 윗 문단의 line segment의 affine hull은 직선이기 때문에, relative interior는 $(0,0)$과 $(1,1)$을 잇는 open segment가 된다.

relative interior의 의의는 interior의 정의 상 empty set이 되어 버려 별로 의미가 없어지는 경우를 극복하는 것이다. 최적화 문제에서 convex domain set의 내부를 표현할 때 interior 대신 relative interior의 개념을 사용해야 할 때가 있다.

Convex sets

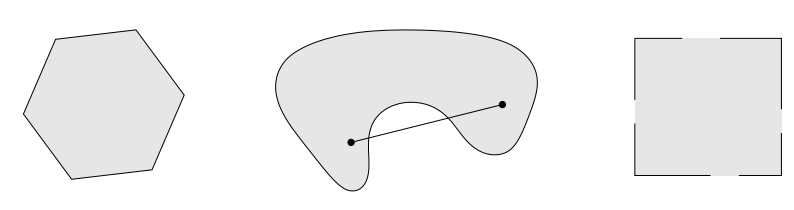
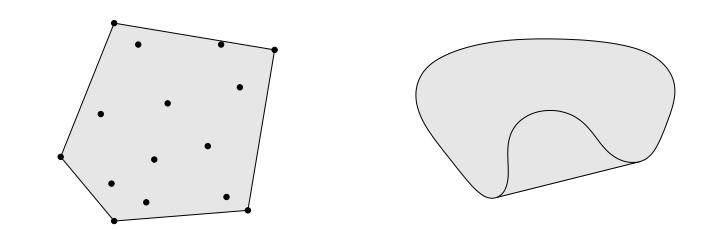
위의 2번과 같은 선형 결합, 즉 아핀 결합과 달리 계수가 0 이상으로 제한되어 있는 경우를 컨벡스 결합(convex combination)이라고 한다. (다른 말로 컨벡스 결합은 아핀 결합의 특수한 경우이고, 모든 convex set은 affine set이기도 하다.) 컨벡스 결합의 가장 간단한 예시는 두 점을 잇는 선분상의 점이다. 이것을 일반화해 어떤 집합이 컨벡스 결합에 대해 닫혀 있으면 이 집합을 convex set이라고 한다. 즉 임의의 두 원소에 대한 내분점(line segment) 역시 그 집합 안에 포함되어 있어야 한다. 또한 임의의 집합을 포함하는 가장 작은 convex set을 convex hull $\text{conv}\,C$ 로 정의한다. 아래 그림은 convex set(맨 왼쪽)과 아닌 것의 예시, 그리고 convex hull의 예시이다.

Cones

위의 3번과 같은 원뿔형 합(conic combination)은 계수의 합이 1이라는 조건이 없고, 계수가 0 이상이라는 조건만 있는 상태이다. 이것의 가장 간단한 예시는 원점을 지나는 반직선이다.
우선 다음을 만족하는 집합 $C$를 cone 혹은 nonnegative homogeneous 이라 한다.

만약 집합 $C$가 아래처럼 cone인 동시에 convex일 경우 convex cone 이라 한다.

$\theta_1,\theta_2$가 모두 0일 경우 원점을 지나며, 둘 중 하나가 0인 경우에 경계선에 해당되며, 모두 0보다 클 경우 내부의 점이 된다.
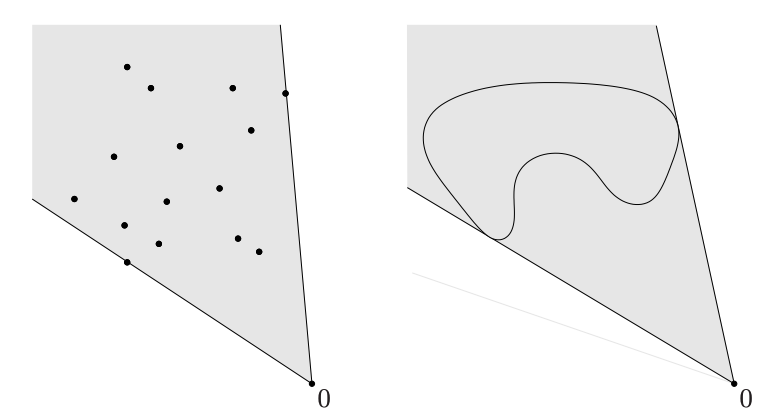
아래처럼 임의의 집합 $C$를 포함하는 가장 작은 convex cone을 conic hull이라 한다.

2. Some important examples

이 섹션에서는 다양한 convex set의 예시를 살펴보자. 기하적인 성질보다는 앞으로 등장할 때 낯설지 않도록 수식적인 정의 위주로 기억하면 충분하다.

Hyperplanes and halfspaces

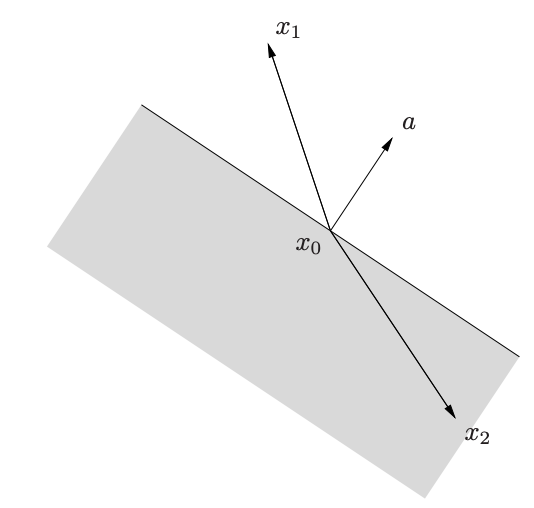
Hyperplane은 평면의 개념을 $n$차원으로 확장한 것으로, $n$차원의 공간을 두 부분으로 가르는 $n - 1$차원의 subset이다. Hyperplane은 아래처럼 linear equation의 해로 나타나며, 따라서 convex set이자 affine set이다.

Hyperplane의 $a$는 normal vector(법선벡터)로 해석될 수 있다. 위의 정의를 $\{x | a^T(x-x_0)=0\}=x_0+a^\perp$으로 다시 정리될 수 있는데, 여기에서 hyperplane에 속하는 임의의 $x$에 대해서 $(x−x_0)$와 a는 직교하는 것을 알 수 있다. 따라서 hyperplane은 $a$의 orthogonal complement의 집합을 $x_0$의 offset만큼 평행이동시킨 것이다.

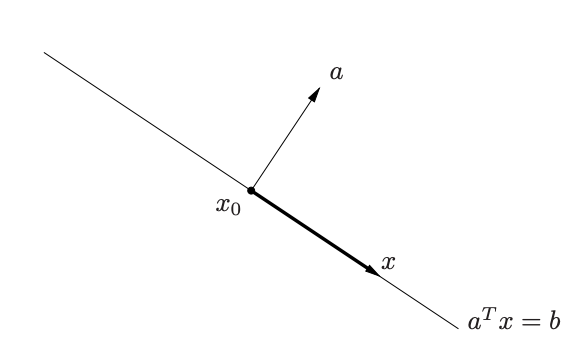
Hyperplane은 아래처럼 두 halfspace를 정의한다. 기하적으로 $(x-x_0)$가 normal vector와 예각을 이루는, 즉 아래 그림의 반 갈린 공간에서 normal vector 방향의 공간은 $\{x | a^Tx \geq b\}$로, 반대쪽(둔각)은 $\{x | a^Tx \leq b\}$로 표현된다.

Euclidean balls and ellipsoids

Euclidean balls은 아래와 같이 정의된다.

동일한 표현으로 아래처럼도 많이 쓴다.

이때 $x_c$는 중심이며, $r$은 반지름이다. 즉 중심 $x_c$으로부터 유클리드 거리가 $r$이하인 집합이므로 3차원에서는 공 모양이 된다.

Ellipsoids(타원체)의 정의는 다음과 같다.

이때 $P$는 symmetric positive definite이고, ellipsoid가 퍼진 모양을 결정한다. 또 $\mathcal{E}$의 반지름의 길이는 $\sqrt{\lambda_i},$ 즉 $P$의 고윳값에 의해 결정된다.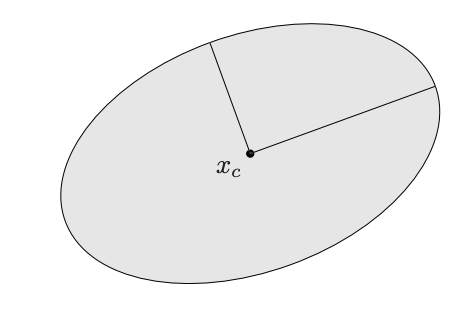
타원체의 또 다른 표현은 아래와 같다.

만약 $A = P^{1/2}$이라 하면 이는 위의 표현과 동일하다. 그러나 만약 $A$가 positive semi-definite지만 singular라면 $R^n$방향으로 뻗어나가지 않고 $A$의 rank와 같은 affine dimension을 가지는 degenerate ellipsoid가 된다.

Norm balls and norm cones

위의 Euclidean ball의 정의를 임의의 norm으로 확장해
$\{x \ | \ \|x - x_c \| \le r \}$로 써도 convex set이다. Norm cone은

로 매개변수 $t$를 포함해 $\mathbb{R}^{n+1}$에서 정의되는데, 정의 그대로 원점에서 반경 $t$만큼 떨어진 점들의 집합이다. Euclidean norm을 통해 정의된 cone을 특별히 second-order cone으로 부른다. 아래 그림은 $\mathbb{R}^{3}$에서 정의된 second-order cone이다.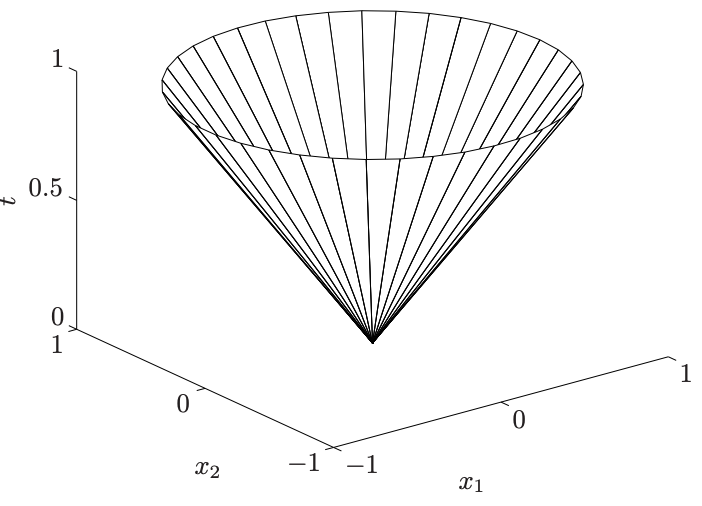

Polyhedra

Polyhedron은 linear inequality와 equality의 교집합으로 정의된다. Affine set(subspace, hyperplane, line)와 ray(반직선), line segment, halfspace는 모두 polyhedron이다.

보통은 아래처럼 행렬로 한 번에 묶어서 많이 표현한다.

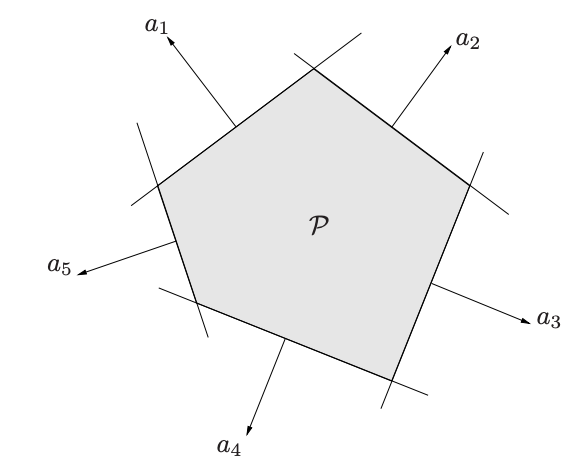
Polyhedron의 종류 중 중요한 것에는 simplex가 있다. Vector $\{v_0,\,v_1,\,...,\,v_k\}$는 $v_1-v_0,\,...,\,v_k-v_0$가 서로 linearly independent일 때 affinely independent라고 부른다. 이들의 convex hull $\text{conv}\{v_0,\,...,v_k\}$를 $k$ dimensional simplex라고 한다. 이것은 아까의 polyhedron의 정의와 다소 이질적으로 보이지만, 변형을 통해 같게 만들 수 있다. 여기서는 생략하겠다. probability simplex는 unit vector $e_1,\,...,e_n \in \mathbb{R}^n$을 통해 정의되는 $(n-1)$차원의 simplex로,
$x \succeq 0,\,\,\mathbf{1}^Tx = 1$를 만족하는 $x$의 집합이다. 이것은 $n$개의 원소를 가진 집합의 probability distribution과 같다. 남은 한 개의 원소의 확률은 합 1의 제약 조건에 의해 정해지므로 자유도는 (n-1)이다.

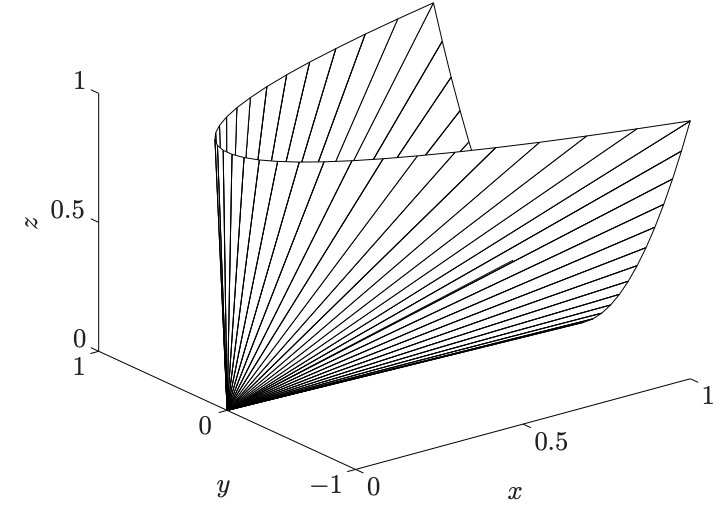
The positive semidefinite cone

$n \times n$ symmetric matrix의 집합을 $\mathbb{S}^n$이라고 하자. Symemetric positive semi-definite matrix의 집합 $\mathbb{S}_+^n$은 positive definiteness의 정의에 의해 convex cone이다. 아래 그림은 $\mathbb{R}^3$상의 $\mathbb{S}_+^2$를 나타낸 것이다. 이 행렬들은 $X = \begin{bmatrix} x & y \\ y & z \end{bmatrix}$로 되어 있다. 그러면 $X\in \mathbb{S}_+^2 \iff x \geq 0,\,z \geq 0,\,xz \geq y^2$이므로 아래처럼 된다.

3. Operations that preserve convexity

집합의 convexity를 유지하거나 convex set을 구성할 수 있게 해주는 연산에 대해 알아보자.

Intersection

집합 $S_1$ 과 $S_2$가 convex이면, $S_1 \cap S_2$ 도 convex이다. 간단하게도 $x,y\in S_1, S_2$이고, 각각의 집합이 convex이므로 $0 \leq \theta \leq 1$에 대해 $\theta x + (1-\theta)y \in S_1,\,S_2$이면 이는 $S_1 \cap S_2$가 convex임과 동일한 진술이다.
가령 polyhedron이 convex set인 이유는 여러 개의 linear equality(hyperplane)과 inequality(halfspace)의 교집합이기 때문이다.

이 진술은 아래처럼 무한대의 intersection으로도 확장될 수 있다.

Example: positive semidefinite cone

positive semi-definite cone $\mathbb{S}^n_+$은 $\bigcap_{z \neq 0} \{ X \in \mathbb{S}^n\, | \,z^TXz \geq 0\}$으로 표현될 수 있다.

$z \neq 0$일 때, $z^TXz$는 $X$에 대한 linear function이므로 집합 $\{X \in \mathbb{S}^n | z^TXz \geq 0\}$은 $\mathbb{S}^n$상의 halfspace이다. 따라서 positive semidefinite cone은 수많은 halfspace의 intersection이라 할 수 있으므로 convex이다.

Affine functions

벡터 $x$에 대하여 정의된 함수가 $f(x) = Ax + b,\,A \in \mathbb{R}^{m\times n},\,b \in \mathbb{R}^m$로 선형변환에 상수가 더해진 꼴이면 $f$를 affine function이라고 한다.

$S \subseteq \mathbb{R}^n$가 convex set일 때, affine function $f: \mathbb{R}^n \rightarrow \mathbb{R}^m$의 image $f(S) = \{ f(x)\,|\,x\in S \}$은 convex이다. 반대로 convex set $S$가 affine function $f: \mathbb{R}^k \rightarrow \mathbb{R}^n$의 image일 때, $S$의 inverse image인 $f^{-1}(S) = \{x|f(x)\in S \}$도 convex이다.

affine function의 가장 간단한 예로는 scaling과 translation을 들 수 있다. 아래처럼 convex set $S \subseteq \mathbb{R}^n$에 대한 스칼라 곱과 평행이동의 image 역시 convex이다.

다른 예로, 아래처럼 몇몇의 coordinates에 대한 convex set의 projection은 convex이다. Projection matrix를 정의하면 이 역시 선형변환이기 때문이다.

또 두 집합 $S_1, S_2$가 각각 convex이면, $S_1+ S_2$도 convex이다. 그 이유는 두 집합의 Cartesian product(convex set)를 아래와 같이 정의했을 때,

$S_1 \times S_2$에 대한 선형변환 $f(x_1,x_2) = x_1 + x_2$를 정의하면 $S_1+S_2$가 선형변환의 image이기 때문이다.

이를 일반화해, 아래처럼 convex set $S_1,\,S_2 \in \mathbb{R}^{n \times m}$에 대한 partial sum $S$ 또한 convex이다.

$S = \{(x, y_1+y_2)|(x, y_1)\in S_1, (x, y_2) \in S_2 \}$

$m = 0$이면 위의 식은 $S_1$과 $S_2$의 교집합이 된다. $n = 0$이면 위의 식은 둘의 합이 된다.

Linear-fractional and perspective functions

The perspective function

수식 그대로 해석하면 perspective function은 벡터의 마지막 원소가 1이 되도록 벡터를 scale한 뒤, 이 마지막 원소를 버리는 것이다. 이 함수는 카메라의 원형인 카메라 옵스큐라(pin hole camera)와 유사하게 해석될 수 있다.

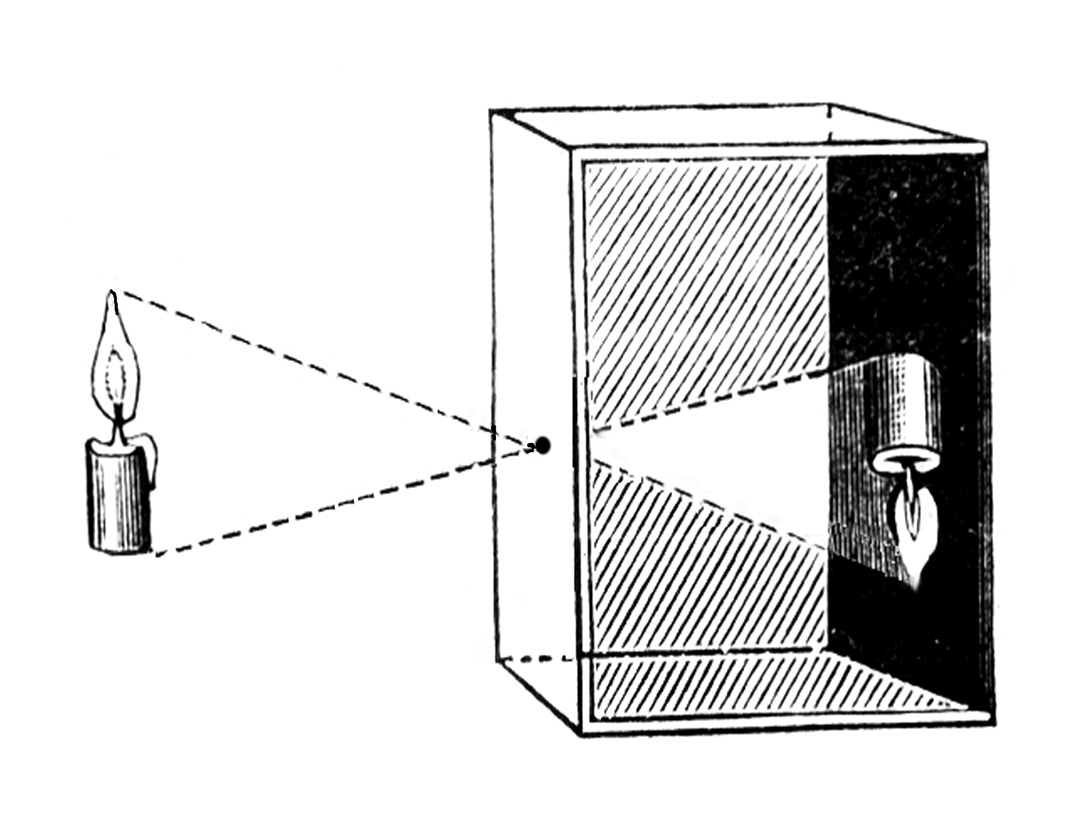
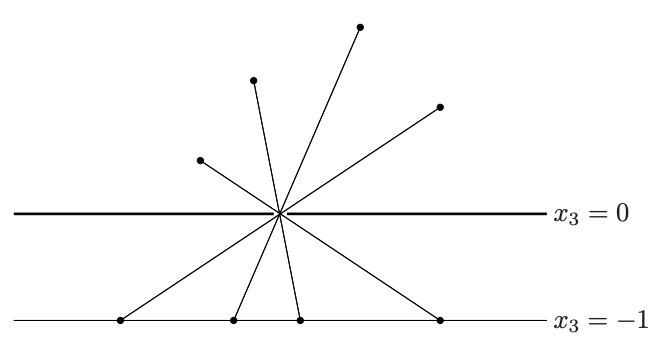
위 그림의 $x_3 = 0$ 부분은 pin hole 부분을 제외하고 빛을 투과시키지 않는 불투명한 판이다. 물체에서 출발한 빛이 작은 구멍을 통과한 뒤, $x_3 = -1$인 image plane에 거꾸로 된 물체의 상이 맺힌다. 예를 들어 $(x_1, x_2, x_3)$이 주어졌을 때, $-(x_1/x_3, x_2/x_3, 1)$이 image plane에 맺히고 마지막 원소를 빼면 $-(x_1/x_3, x_2/x_3)$이 된다. 즉, perspective function을 통해 $(x_1, x_2, x_3)$이 $-(x_1/x_3, x_2/x_3)$으로 대응되는 것을 알 수 있다.
Convex set $C$에 perspective function을 취해도 convex이며, $C$에 대한 perspective function의 inverse image 역시 convex이다.

Linear-fractional functions

Linear fractional function은 affine function과 perspective function의 결합으로, 둘을 일반화한 것이다. $g: \mathbb{R}^n \rightarrow \mathbb{R}^{m+1}$이 아래와 같이 정의되었다고 하자.

이때 linear-fractional function $f: \mathbb{R}^{m+1} \rightarrow \mathbb{R}^{m}$은 아래와 같이 정의된다. 즉 $x$에 affine function을 취한 뒤 perspective function을 다시 취해 주는 것이다.

linear-fractional function의 간단한 예로는 conditional probability를 들 수 있다.
$u$와 $v$가 각각 $\{1,\,2,\,...,\,n\},\,\{1,\,...,\,m\}$까지의 값을 가질 수 있는 확률변수라고 하자. 그리고 둘의 joint probability matrix $p_{ij} = \ \mathbb{P}(u=i,\,v=j)$가 주어졌을 때, conditional probability $f_{ij} =\mathbb{P}(u=i\,|\,v=j)$는 아래와 같이 구할 수 있다.

즉 conditional probability는 어떤 joint probability를 marginal sum으로 normalize한 것과 같으므로 $x = p_{\cdot j},\,A = I,\,c = \mathbf{1}$로 설정한 linear fractional function과 같다.
linear fractional function $f$와 convex set $C$에 대해 $C$가 $\text{dom}\,f$에 속한다면 $f(C)$도 convex이고, $C$에 대한 inverse image 역시 convex이다.