[Week 4] Duality [2]

ESC·2023년 12월 13일

2023-Winter

목록 보기

8/10

이번 포스트의 내용을 잘 이해하기 위해서는 바로 전 글에서 언급된 weak duality와 strong duality의 특징, 조건, 다양한 관점에서의 해석 등을 잘 숙지해두는 것이 중요하다. 첫번째로, 우리는 이와 같은 문제들을 시각적으로 다루면서 이해해볼 수 있다.

1. Geometric interpretation

다음과 같이 하나의 Inequality constraint만을 가진 Primal problem을 가정하자.

\begin{aligned} &\text{minimize} \quad f_0(x) \\ &\text{subject to} \ \ \ f_1(x)\le 0 \end{aligned}

이때, 임의의 x값에 따라 정해지는 constraint function의 함숫값을 u, objective function의 함숫값을 t로 둔다면 순서쌍 (u, t)로 구성된 새로운 집합 G를 정의할 수 있다.

G=\{ (u,t)\ | \ f_1(x)=u, \ f_0(x)=t, \ x \in D \}

이제 domain $D$ 를 u-t plane 상에 매핑한 $G$ 가 다음과 같이 그려지는 경우를 생각해보자. Feasible한 영역은 $f_1(x)$ 의 값이 0보다 작거나 같은, 즉 $u$ 가 0보다 작거나 같은 부분이 된다. 이때의 optimal point, 해당 문제에서는 최소점에서의 t값이 우리가 구하고자 하는 $p^*$ 이다. 이것이 primal problem의 geometric interpretation이라고 할 수 있다.

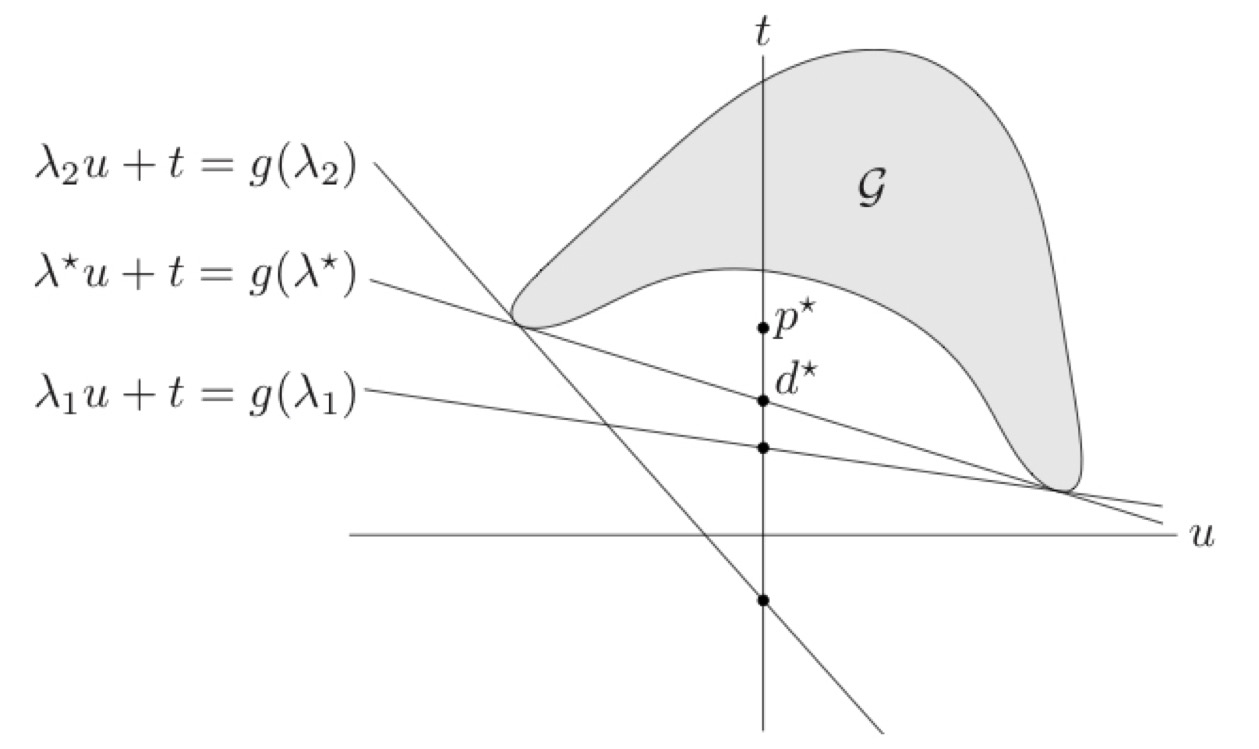
이제 Dual problem으로 넘어가서, 동일한 문제에 대한 Lagrange Dual function은 아래와 같이 정의된다. 마찬가지로 set G가 정의된 상태에서 이를 벡터의 형태로 나타내보면 결국 다음과 같은 내적 값을 최소화하는 문제가 된다.

\inf_{x\in D} \{\lambda f_1(x) + f_0(x) \}=\inf_{(u,t)\in G} \{\lambda u + t \}= \inf_{(u,t)\in G} \{(\lambda,1)^T (u,t) \}

위의 그림을 보고 임의의 $\lambda$ 값이 고정되어 있다고 해보자. 그렇다면 $(u, t)$ 에 대해서 $( \lambda, 1)$ 과의 내적 값이 0, 즉 $( \lambda, 1)$ 이라는 벡터와 수직인 상태를 생각할 수 있겠고, 기울기는 $-\lambda$ 가 된다. 이때 $t$ 값이 최소가 되기 위해서는 이 직선이 $(\lambda, 1)$ 에 네거티브한 방향으로 최대한 움직이되, set $G$ 의 적어도 한 점과 만날 수 있도록 해주어야 한다. 그리고 이러한 경우는 set $G$ 의 한 점만을 지나면서 $G$ 를 하나의 Half space에 완전히 포함시키므로 supporting hyperplane의 역할을 할 수 있다.

이처럼 $\lambda$ 값을 fix하고 (즉 기울기를 고정하고), dual을 도출하는 (즉 이 직선을 march down하는) 일련의 과정을 모든 가능한 $\lambda$ 값에 대해 전부 적용했다고 생각해보라. 실제로 기울기를 계속해서 조정했을 때, 첫째, 모든 $g$ 값은 $\lambda$ 값과 무관하게 p*보다 작거나 같은 곳에 위치하고, 둘째, $g$ 가 계속 증가하다가 어느 순간 다시 감소하는 것을 관찰할 수 있다.

바로 이 변화 지점, 즉 $g$ 의 최댓값이 dual problem의 optimal point인 $d^*$ 가 되는 것이다. 이때의 $p^*-d^*$ 값을 ‘Duality gap’, 이 두 점 간의 차이가 안나는 경우를 Strong duality라고 정의했다.

이를 일반적인 케이스에 대해서 수식적으로 확장을 시켜본다면 다음과 같다. Set G는 inequality constraint, equality constraint, objective function 전부의 함숫값들의 집합으로 정의될 것이고, feasible한 영역 내에서의 t의 최저점인 $p^*$ 와 해당 케이스의 라그랑지안, dual function은 순서대로 아래와 같이 표현된다.

G=\{ (f_1(x),...,f_m(x),h_1(x),...,h_p(x), f_0(x)) \in R^m \times R^p \times R \ | \ x \in D\} \\

p^*=\inf \{ t \ | \ (u, v, t) \in G, \ u \preceq 0, \ v=0\} \\ (\lambda, \nu, 1)^T(u, v, t) = \sum_{i=1}^m \lambda_i u_i + \sum_{i=1}^p \nu_i v_i+t \\g(\lambda, \nu)=\inf\{ (\lambda, \nu,1)^T(u, v, t)\ | \ (u, v, t) \in G\}

만약 infimum이 $-\infin$ 이 아니라면, 우리가 그림으로 확인한 것처럼 이 부등식이 G의 supporting hyperplane을 정의할 수 있다.

(\lambda, \nu, 1)^T(u, v, t) \geq g(\lambda, \nu)

\begin{aligned} p^*&= \inf \{ t\ |\ (u, v, t) \in \mathcal{G}, u \preceq 0, v=0\} \\ &\geq \inf \{ (\lambda, \nu, 1)^T(u, v, t)\ |\ (u, v, t) \in \mathcal{G}, u \preceq 0, v=0\} \\ &\geq \inf \{ (\lambda, \nu, 1)^T(u, v, t)\ |\ (u, v, t) \in \mathcal{G}\} \\ &=g(\lambda, \nu) \end{aligned}

그렇다면 $p^*$ 의 하한보다는 동일한 제약 조건을 공유하는 상태의 내적 값의 하한이 작거나 같아지겠고, 기본적으로 제약 조건이 있을 때보다 없을 때 더 작거나 같게 minimize 할 수 있다는 아이디어로부터 우리는 $p^*$ 와 앞서 정의한 dual function의 값 사이의 관계를 위와 같이 도출할 수 있다.

2. Strong duality and convexity

이번에는 primal problem의 convexity와 dual problem의 strong duality를 어떤 식으로 관련지을 수 있을 지 생각해보자. 앞선 포스트에서 다룬 Slater’s theorem을 떠올려보라. 이는 Primal 문제가 convex이고 strictly feasible한 x가 하나 이상 있다면 (Slater’s condition을 만족한다면) strong duality가 만족된다는 것이었습니다. 이를 그림을 통해 대략적으로 살펴보겠다.

A=\{ (u, t) \ | \ \exist x \in D, \ f_0(x) \le t, \ f_1(x) \le u\}

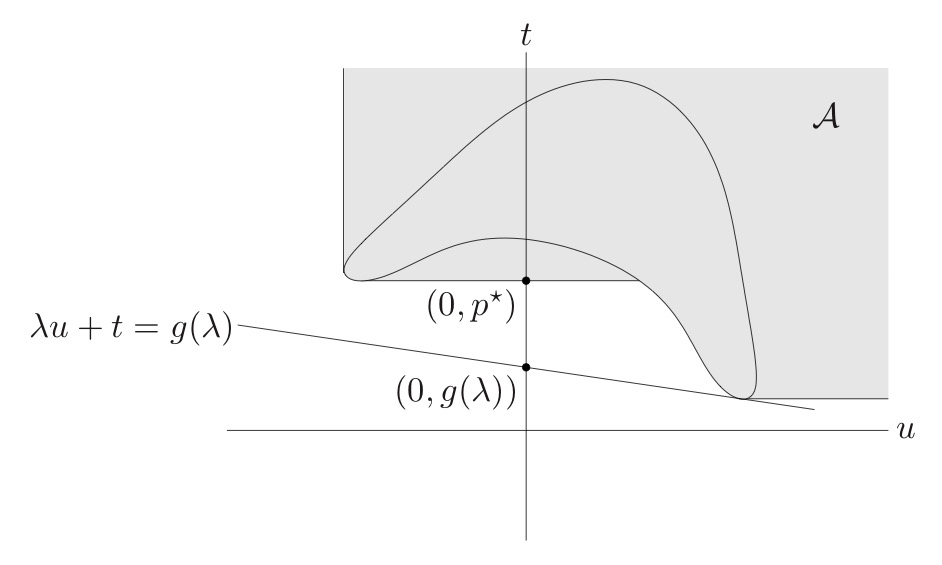
이번에는 set $G$ 대신 set $A$ 를 다음과 같이 정의하자. set $A$ 에 해당하는 부분을 전부 칠해보면 set $G$ 에서의 $u$ 값과 $t$ 값 중 적어도 하나가 큰 모든 부분들이 칠해지기 때문에, 이를 set $G$ 에 대한 일종의 epigraph라고 이해할 수 있을 것이다. 그리고 이와 같이 확장된 상황에서는 $p^*$ 가 set $A$ 의 boundary에 속하기 때문에 $p^*$ 역시 set $A$ 의 다른 원소들과 마찬가지로 마찬가지로 벡터의 내적 형태로 표현이 될 수 있을 것이고, $p^*$ 와 $d^*$ 의 관계로부터 다음과 같은 부등식을 얻을 수 있다.

p^* = (\lambda, 1)^T(0, p^*) \geq g(\lambda, \nu)

이때 등호가 성립하는 상태를 strong duality라고 했었는데, 왼쪽의 vector form과 오른쪽의 $g$ 사이에 등호가 성립한다는 것은 곧 $p^* \geq g(\lambda, \nu)$ 가 set $A$ 의 nonvertical supporting hyperplane이라는 사실을 의미한다. 만약 위의 예제에서 primal 문제가 convex해서 epigraph가 convex 했다면 $(0, p^*)$ 에서의 supporting hyperplane이 존재했을 것이다. 특히 이때는 strictly feasible한 $x$ 들이 존재하기 때문에, 이들을 전부 half space에 포함시키기 위해서는 hyperplane이 수직이 아니어야 한다.

이처럼 Primal problem의 optimal한 값에서 non-vertical supporting hyperplane이 존재한다면 이 문제는 strong duality를 만족하고, 이와 같은 존재성을 대체적으로 보장해줄 수 있는 것이 바로 Primal problem의 convexity임을 그림을 통해 확인해보았다.

3. Saddle point interpretation

교재의 5.4절에서는 Lagrange Duality를 색다른 관점으로 해석한다. Equality constraint가 없는 simple problem에서, 다음과 같은 등식에 대해 생각해보자.

\begin{aligned} \sup_{\lambda \succeq0} L(x, \lambda)&= \sup_{\lambda \succeq0} (f_0(x)+ \sum_{i=1}^m \lambda_i f_i(x)) \\ &= \begin{cases} f_0(x) &f_i(x) \leq0, \ i=1, ...,m \\ \infin &\text{otherwise.} \end{cases} \end{aligned}

해당 식에서 $\lambda$ 값이 non-negative일 때, 만약 각 $f_i(x)$ 값들이 0보다 작거나 같다면 (inequality constraint를 만족한다면) supremum은 $f_0(x)$ 가 되며 그렇지 않은 경우에 대해서는 끊임 없이 증가하기에 $\infin$ 가 된다. 그렇다면 $f_0(x)$ 즉 primal problem의 optimal value인 $p^*$ 를 $\sup_{\lambda \succeq0} L(x, \lambda)$ 의 하한이라고 여길 수 있으며, dual function의 정의를 통해 아래와 같은 구조를 관찰할 수 있다.

p^*= \inf_x \ \sup_{\lambda \succeq 0} L(x, \lambda), \ \ d^*= \sup_{\lambda \succeq 0} \ \inf_x L(x, \lambda)

앞서 확인한 $d^* \leq p^*$ 에 이를 적용하면 다음과 같다.

\sup_{\lambda \succeq 0} \ \inf_x L(x, \lambda) \leq \inf_x \ \sup_{\lambda \succeq 0} L(x, \lambda)

이러한 부등식을 general한 경우에서는 max-min inequality라고 칭한다. 만약 strong duality가 충족된다면 등호가 성립하므로 minimizing 후 maximizing을 한 것과 maximizing 후 minimizing을 하는 것이 동일해지게 된다. 이 때를 max-min inequality적 관점에서 “saddle point property를 만족한다”고 간주하는 것이다.

[참고] 일반적으로 미분 값이 0임은 해당 점이 Local minimum 또는 maximum일 필요조건으로 작용했는데, Saddle point가 바로 이 둘이 필요충분조건이 되지 못하도록 하는 대표적인 케이스이다.

이러한 saddle point의 개념을 수식으로 표현해보면 다음과 같다.

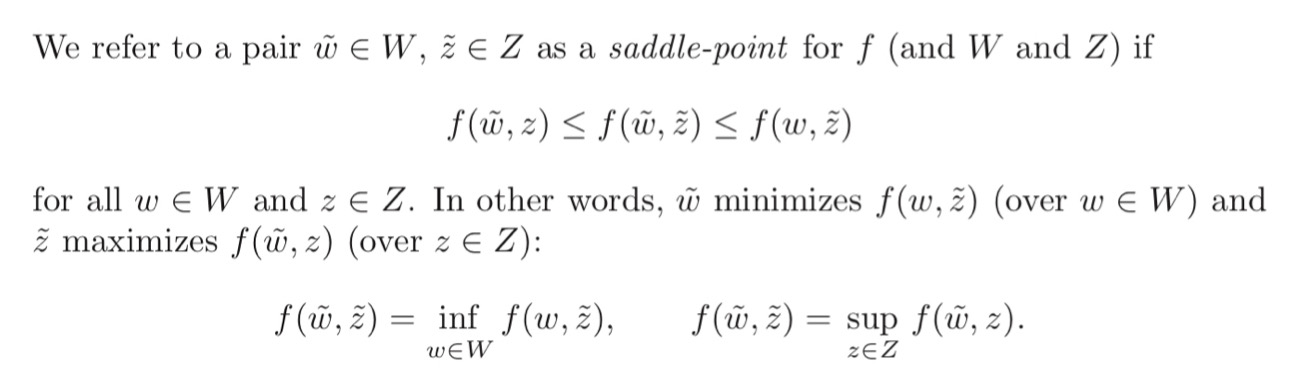
풀어서 이해하자면, $f(\tilde{w}, z)$ 를 최대화할 수 있는 $z$ 는 $\tilde{z}$ 이고, $f(w, \tilde{z})$ 를 최소화할 수 있는 $w$ 는 $\tilde{w}$ 이다. 즉 $f(\tilde{w}, \tilde{z})$ 는 어느 관점에서 보는 지에 따라 infimum이기도, supremum이기도 하다. 이처럼 특정 점이 어느 방향에서 보면 극댓값을 갖고 어느 방향에서 보면 극솟값을 갖는 경우를 Saddle point라고 하고, 이와 같은 점은 최적화 기법을 방해할 수 있다고 알려져 있다.

Lagrange duality에 대한 논의로 돌아와서, primal problem은 $x^*$ 에서 최솟값 $p^*$ 를 가지고, dual problem은 $\lambda^*$ 에서 최댓값 $d^*$ 를 가진다. 그렇다면 strong duality를 만족하는 $p^*=d^*$ 인 경우를 일종의 saddle point로 이해할 수 있을 것이다.

4. Stopping criterion

Stopping criteria의 역할은 한 마디로 알고리즘을 ‘적당히 돌아가게’하는 것이다. 조기 종료처럼 적당한 순간에 알고리즘을 멈춤으로써 computational cost를 아끼는 것이 때로는 이로울 수 있다. 이번 섹션에서는 이러한 stopping의 기준을 설정할 때 어떻게 duality gap의 컨셉을 이용할 수 있는 지를 이야기하고자 한다.

g(x) \leq d^* \leq p^* \leq f(x)

Primal optimal과 dual optimal의 정의와 둘 사이의 관계를 통해 얻은 위의 부등식을 토대로, 아래의 부등식 및 포함 관계를 손쉽게 도출할 수 있다.

f_0(x)-p^* \leq f_0(x)-g(\lambda, \nu) \\ p^* \in [g(\lambda, \nu), f_0(x)], \ d^* \in [g(\lambda, \nu), f_0(x)]

고른 점에 따라서 달라질 수 있는 것은 바로 $f_0(x)-g(\lambda, \nu)$ , 즉 선택한 변수들에 대한 일종의 ‘duality gap’ 이다. 이는 주어진 feasible point가 얼마나 suboptimal 한 지 보여주는 지표가 되는데, 이제부터 이 차이를 $\epsilon$ 으로 표기하도록 하자. $\epsilon=0$ 인 가장 이상적인 상황에서는 당연히 $g(x) = d^* = p^* = f(x)$ , 즉 strong duality가 만족된다. 이처럼 이 gap이 작아질수록 이상적인 상황에 가깝다면, 최적화 문제를 이러한 gap을 다루는 문제로 이해할 수 있겠다.

f_0(x^{(k)})-g(\lambda^{(k)}, \nu^{(k)}) \leq \epsilon_{\mathsf{abs}} \\[0.8ex] \frac{f_0(x^{(k)})-g(\lambda^{(k)}, \nu^{(k)})}{g(\lambda^{(k)}, \nu^{(k)})} \leq \epsilon_{\mathsf{rel}}

따라서 사용자가 ‘목표로 하는’ $f_0(x)$ 와 $g(\lambda, \nu)$ 간의 절대적 차이 또는 상대적 차이를 stopping criteria인 $\epsilon$ 으로 입력하여, 둘의 차이가 허용된 오차 $\epsilon$ 보다 작아지는 순간 알고리즘이 멈출 수 있도록 설계할 수 있다.

5. Complementary slackness and KKT Condition

이번에는 어떤 primal problem과 dual problem 각각에 feasible한 solution이 서로의 optimal solution이 되기 위한 조건이 무엇인지 살펴보자. Strong duality가 충족되었고, $x^*$ 가 primal optimal point, $(\lambda^*, \nu^*)$ 가 dual optimal point인 상황을 가정하고 아래의 식을 보라.

\begin{aligned} f_0(x^*) &= g(\lambda^*, \nu^*) \\ &= \inf_x \ (f_0(x)+\sum_{i=1}^m \lambda^*_i f_i(x)+ \sum_{i=1}^p \nu_i^* h_i(x)) \\ &\leq f_0(x^*)+\sum_{i=1}^m \lambda^*_i f_i(x^*)+ \sum_{i=1}^p \nu_i^* h_i(x^*) \\ &\leq f_0(x^*) \end{aligned}

먼저 strong duality에 의해 첫 줄의 등호가 성립하고, dual function의 정의를 풀어서 쓴 것이 두 번째 줄이 되겠다. 그리고 라그랑지안의 infimum은 해당 식에 임의의 x를 대입했을 때의 값보다 항상 작거나 같을 것이므로 둘째 줄과 셋째 줄 간의 대소관계를 표기해줄 수 있다. 이때 해당 변수값들을 feasible한 영역에서 가져왔으므로, $\lambda$ 가 non-negative이고 inequality constraint와 equality constraint가 모두 만족되어야 한다. 따라서 셋째 줄과 넷째 줄 사이의 대소관계가 성립된다. 결국 첫 줄과 마지막 줄이 동일하므로 이 모든 식의 값이 같아지겠고, $x^$는 라그랑지안의 minimizer 중 하나가 된다.

여기서 셋째 줄과 넷째 줄을 다시 보자. 둘 사이의 등호가 성립하기 위해서는 $\sum_{i=1}^m \lambda^*_i f_i(x^*)$ 가 0이 되어야 하며, non-positive한 값들의 합이 0이라는 것은 곧 더해지는 모든 항들의 값이 0이 되어야 함을 의미한다. 즉 $\lambda^*_i$ 와 $f_i(x^*)$ 중 적어도 하나가 0이 되어야 하므로 다음과 같은 표현이 성립한다.

\lambda_i^* f_i(x^*)=0, \ i=1, ..., m. \quad \text{That is}, \ \begin{cases} \lambda_i^*>0 &\Rightarrow f_i(x^*)=0 \\ f_i(x^*)<0 &\Rightarrow \lambda_i^*=0 \end{cases}

우리는 해당 조건을 ‘Complementary slackness’라고 칭한다. 이 특성은 strong duality 하의 모든 primal optimal과 dual optimal 사이에서 성립한다. Complementary slackness는 바로 뒤에 다룰 KKT condition을 이해하는 데 사용된다. KKT condition은 무엇인가? 결론부터 이야기하자면 KKT condition은 strong duality에 대한 필요충분조건이 될 수 있고, primal problem의 optimality를 보장해줄 수 있으면서 그 해에 대한 해결 방법을 제시해줄 수 있다.

KKT condition에 대해 알아보기 위해 먼저 nonconvex한 primal problem을 가정하자. $x^*$ 와 ( $\lambda^*, \nu^*$ )가 duality gap이 0인 primal problem과 dual problem의 optimal point일 때, $x^*$ 가 라그랑지안의 값을 최소화하는 $x$ 값이 되므로 아래의 gradient가 0이 되어야 한다.

\nabla f_0(x^*)+\sum_{i=1}^m \lambda_i^* \nabla f_i(x^*)+ \sum_{i=1}^p \nu_i^* \nabla h_i(x^*)=0

이 조건을 이제부터 ‘Stationarity’라고 칭할 것이다. 이제 strong duality와 관련해서 언급된 모든 조건들 - Primal feasibility, Dual feasibility, Complementary slackness, Stationarity를 나열해보자.

{\begin{aligned} &f_i(x^*)\le0, \ i=1, ..., m &&(1) \\[1.0ex]&h_i(x^*)=0, \ i=1, ..., p &&(2) \\[1.0ex] &\lambda_i^* \ge 0, \ i=1, ..., m &&(3) \\[1.0ex] &\lambda_i^* f_i(x^*)=0, \ i=1, ..., m &&(4) \\ &\nabla f_0(x^*)+\sum_{i=1}^m \lambda_i^* \nabla f_i(x^*)+ \sum_{i=1}^p \nu_i^* \nabla h_i(x^*)=0 &&(5) \end{aligned}}

이 다섯개의 조건을 묶어서 Karush-Kuhn-Tucker condition 즉 KKT condition이라고 부르는 것이다. 정리하자면 이러한 일반적인 경우 ‘Strong duality가 만족된다면, primal 및 dual optimal point의 쌍은 KKT condition을 만족한다’. KKT condition이 strong duality에 대한 필요조건이 되는 것이다.

그리고 어떤 특별한 전제가 충족이 될 때 KKT는 strong duality의 충분조건이 되기도 한다. 그 전제 조건이 바로 Primal problem convexity이고, convexity가 최적화 문제에 있어서 중요하게 생각되는 이유 중 하나이다. Primal problem이 convex, 즉 inequality constraint가 convex하고 equality constraint가 affine일 때 KKT condition을 만족하는 $\tilde{x}$ 와 ( $\tilde{\lambda}, \tilde{\nu}$ )의 쌍이 있다고 가정하면, 다음의 모든 성질이 만족될 것이다.

{\begin{aligned} &f_i(\tilde{x})\le0, \ i=1, ..., m &&(1) \\[1.0ex]&h_i(\tilde{x})=0, \ i=1, ..., p &&(2) \\[1.0ex] &\tilde{\lambda}_i \ge 0, \ i=1, ..., m &&(3) \\[1.0ex] &\tilde{\lambda}_i f_i(\tilde{x})=0, \ i=1, ..., m &&(4) \\ &\nabla f_0(\tilde{x})+\sum_{i=1}^m \tilde{\lambda}_i \nabla f_i(\tilde{x})+ \sum_{i=1}^p \tilde{\nu}_i \nabla h_i(\tilde{x})=0 &&(5) \end{aligned}}

이때 Stationarity를 보면 라그랑지안의 gradient가 $\tilde{x}$ 에서 0의 값을 갖는데, convex function의 경우 하나의 minimum 값만을 가질 수 있고 이때의 gradient가 0이 되므로 $\tilde{x}$ 가 라그랑지안을 최소화하는 $x$ 값임이 보장될 것이다. 따라서 다음과 같이 식을 전개할 수 있고 primal optimal과 dual optimal 사이에 gap이 존재하지 않는 상황이 된다.

\begin{aligned} g(\tilde{\lambda}, \tilde{\nu}) &= L(\tilde{x}, \tilde{\lambda}, \tilde{\nu}) \\ &= f_0(\tilde{x}) + \sum_{i=1}^m \tilde{\lambda}_i f_i(\tilde{x}) + \sum_{i=1}^p \tilde{\nu}_i h_i(\tilde{x}) \\ &= f_0(\tilde{x}) \end{aligned}

이로부터 우리는 ‘어떤 $x$ , ( $\lambda, \nu$ )의 쌍이 KKT condition을 만족할 때 strong duality가 성립된다’는 사실을 알 수가 있고 이때의 point가 primal 및 dual optimal이라고 해석할 수 있겠다.

이번 포스트의 내용을 정리해보자. Strong duality가 만족될 때, primal optimal을 바로 구하는 대신 dual optimal을 구하는 것이 더 쉽다면 dual problem의 해를 구함으로써 primal problem을 다룰 수 있다. Strong duality는 (a) Slater’s condition을 만족하면서 convex할 때, 그리고 (b) KKT condition을 만족하면서 convex할 때 대체적으로 충족될 수 있다. 특히 후자의 경우 KKT condition의 해가 primal 및 dual optimal point가 되므로 이를 활용해 최적화 문제의 해를 구하는 다양한 알고리즘들이 연구되고 있다. 이상으로 포스트를 마치도록 하겠다.

ESC

@Yonsei University

이전 포스트

[Week 4] Duality [1]

다음 포스트