[Week 4] Duality [1]

ESC·2023년 12월 13일

2023-Winter

목록 보기

7/10

*세션 교재: Convex Optimization – Boyd and Vandenberghe. Ch.5.

이번 포스트는 최적화 문제에서 가장 중요하게 여겨지는 개념 중 하나인 Duality (쌍대성)에 대해 다룬다. 이는 ‘어떤 조건 g를 만족하는 함수 f의 최댓값 또는 최솟값을 찾을 때, 그 찾고자 하는 값이 f와 g의 접점에 존재할 수 있다’는 가능성에서 출발한다. 하나의 최적화 문제는 Primal problem과 Dual problem의 두 가지 관점에서 다뤄질 수 있고, 한 쪽의 상한은 한 쪽의 하한이 된다. 앞으로의 두 포스트를 통해 이러한 관계가 어떻게 성립될 수 있는 것이며 왜 중요한지를 알아보도록 하자.

1. The Lagrange dual function

먼저 다음과 같은 기본적인 형태의 최적화 문제에 대해 생각해보자.

{\begin{aligned}&{\text{minimize }} &&f_0(x) \\[0.5ex]&{\text{subject to }} &&f_i(x) \le 0 , \ i=1,...,m \\[0.5ex]& &&h_i(x) = 0 , \ i=1,...,p\end{aligned}}

이 문제에 대한 Domain이 non-empty set이고, 그 optimal value가 $p^*$ 라고 가정하자. 이때의 최적화 문제가 Convex일 필요는 없다.

Lagrangian duality의 기본적인 아이디어는 최적화 문제의 모든 제약식에 라그랑주 승수 (Lagrange multiplier)를 곱하고 목적 함수에 더해줌으로써 제약이 있는 문제를 제약이 없는 문제 형태로 바꾸어 표현하는 것이다. 그 형태는 아래와 같다.

\begin{aligned} &L : \mathbb{R}^n \times \mathbb{R}^m \times \mathbb{R}^p \rightarrow \mathbb{R} \\ &L(x,\lambda,\nu)=f_0(x) + \sum_{i=1}^m \lambda_if_i(x) + \sum_{i=1}^p \nu_ih_i(x) \\ &\text{with} \ \ \mathbf{dom} \ L=\mathcal{D}\times\mathbb{R}^m\times\mathbb{R}^p.\end{aligned}

이때 $\lambda, \nu$ 를 Dual variables 또는 Lagrange Multiplier라고 부른다. 이처럼, Lagrangian이란 목적함수와 제약함수 가중합을 하나의 식으로 합치는 것을 의미한다. 그리고 이 개념을 이용하여 우리는 Lagrange dual function을 정의할 수 있다.

\begin{aligned} &\text{Let} \ g: \mathbb{R}^m\times\mathbb{R}^p \rightarrow \mathbb{R}. \quad \text{For}\ \lambda \in \mathbb{R}^m \ \text{and} \ \nu \in \mathbb{R}^p, \\ &g(\lambda, \nu)=\inf_{x\in\mathcal{D}}L(x,\lambda,\nu)=\inf_{x\in\mathcal{D}}[ f_0(x)+\sum_{i=1}^m\lambda_if_i(x)+\sum_{i=1}^p\nu_ih_i(x)] \end{aligned}

Lagrange dual function은 최적화 문제의 Lagrangian을 최소화하는 의미를 지닌다. 따라서 만약 라그랑지안이 $x$ 에 대해 Unbounded라면 dual function의 값은 $-\infin$ 이 된다. 참고로 이 정의는 Affine function 족의 pointwise infimum이므로, 최적화 문제가 convex 하지 않더라도 dual function은 항상 concave이다.

2. Lower bounds on optimal value

중요한 것은, 이러한 dual function이 optimal value $p^*$ 에 대한 하한으로 작용할 수 있다는 사실이다. 즉 조건(여기서는 $\lambda \succeq 0$ )을 만족하는 모든 $\lambda$ 와 $\nu$ 에 대해, $g(\lambda, \nu)$ 값은 $p^*$ 보다 작거나 같다.

Proof For any $\lambda \succeq 0$ and any $\nu$ , $g(\lambda, \nu) \le p^*$

$\tilde{x}$ 를 최적화 문제에 대한 feasible point라고 가정하자. 즉 주어진 조건인 $f_i(\tilde{x}) \leq0, \ h_i(\tilde{x})=0, \ \lambda \succeq 0$ 이 전부 만족된 상황이라면, 각 term이 non-positive이기 때문에 다음이 만족된다.

\sum_{i=1}^m \lambda_if_i(\tilde{x}) + \sum_{i=1}^p \nu_ih_i(\tilde{x}) \le 0

이때 양변에 동일하게 $f_0(\tilde{x})$ 를 더해줌으로써 좌변을 Lagrangian으로 만들어줄 수 있다.

L(\tilde{x},\lambda, \nu) = f_0(\tilde{x}) + \sum_{i=1}^m \lambda_of_i(\tilde{x})+\sum_{i=1}^p\nu_ih_i(\tilde{x}) \le f_0(\tilde{x})

여기서 $\tilde{x}$ 에는 feasible point가 되기 위한 제약조건이 여럿 붙어있다. 그렇다면 우리는 $\tilde{x}$ 대신 제약조건이 (Domain에 속하는 것 외에는) 없는 상태의 어떤 $x \in \mathcal{D}$ 를 식에 대입했을 때 식의 값을 더욱 작거나 같게 만들 수 있음을 직관적으로 받아들일 수 있다. 이를 식으로 표현하면 곧 $g(\lambda, \nu)$ 가 되므로, 아래와 같은 관계가 도출된다.

\therefore g(\lambda,\nu)=\inf_{x \in \mathcal{D}} L(x,\lambda,\nu) \le L(\tilde{x},\lambda, \nu) \le f_0(\tilde{x})

따라서, $g(\lambda,\nu) \le f_0(\tilde{x})$ 가 모든 feasible point $\tilde{x}$ 에 대해 성립하므로 $g(\lambda, \nu) \le p^*$ 은 성립한다.

(Example) LP에 대한 Lagrange dual function 도출하기
아래와 같은 LP의 standard form이 있다.
$\begin{aligned} &\text{minimize} \quad c^Tx \\ &\text{subject to} \ \ \ Ax=b, \ x \succeq 0 \end{aligned}$
정의를 따라가면 이에 대한 Lagrangian과 dual function을 어렵지 않게 구할 수 있다.
$L(x,\lambda, \nu)=c^Tx-\sum_{i=1}^n\lambda_ix_i+\nu^T(Ax-b)=-b^T\nu+(c+A^T\nu-\lambda)^Tx \\ g(\lambda,\nu) = \inf_xL(x,\lambda,\nu) =-b^T\nu+\inf_x(c+A^T\nu-\lambda)^Tx$
$g(\lambda, \nu)$ 는 $A^T\nu-\lambda+c=0$ 을 만족할 때 $-b^T\nu$ 값이 최소가 되고 이외에는 음의 무한대 값을 가진다. 따라서 LP의 lower bound는 $\lambda \succeq0, \ A^T\nu-\lambda+c=0$ 을 만족할 때 $-b^T\nu$ 가 된다.
$g(\lambda, \nu) = \begin{cases} -b^T\nu \quad (A^T\nu-\lambda+c=0) \\ -\infin \ \ \ \quad \text{otherwise} \end{cases}$

3. The Lagrange dual function and conjugate functions

*Conjugate function: Maximum gap between the linear function $y^Tx$ and $f(x)$

이번에는 dual function과 conjugate function 간의 관계를 알아봄으로써 dual function을 더욱 단순화된 conjugate function으로 나타내보자. 함수 $f: \mathbb{R}^n \rightarrow \mathbb{R}$ 에 대한 conjugate function $f^*$ 는 다음과 같이 정의된 바 있다.

f^*(y) = \sup_{x \in \mathbf{dom} f} (y^Tx-f(x))

우리는 매우 간단한 프로토타입인, $x=0$ 이 제약 조건으로 주어졌을 때 $f(x)$ 를 최소화하는 문제를 통해 둘 간의 관계를 유추할 수 있다.

g(\nu)=\inf(f(x)+\nu^Tx)=-\sup((-\nu)^Tx-f(x))=-f^*(-\nu)

부호 term을 추가함으로써 우리는 infimum을 supremum으로 전환할 수 있고, 이는 곧 conjugate function의 형태가 된다. 이를 조금 더 일반화 해보면 아래와 같다.

\begin{aligned} &\text{minimize} \quad f_0(x) \\ &\text{subject to} \ \ \ Ax \preceq b, \ Cx=d \end{aligned}

위의 최적화 문제를 conjugate function을 이용하여 단순화해보자.

\begin{aligned} g(\lambda, \nu) &= \inf_x (f_0(x)+\lambda^T(Ax-b) +\nu^T(Cx-d)) \\ &=-b^T\lambda-d^T\nu+\inf_x(f_0(x)+(A^T\lambda+C^T\nu)^Tx) \\ &= -b^T\lambda-d^T\nu-f_0^*(-A^T\lambda-C^T\nu) \end{aligned}

이때 $g$ 의 domain은 $f_0^*$ 의 domain인 $\mathbf{dom} \ g=\{(\lambda,\nu) | -A^T\lambda-C^T\nu \in \mathbf{dom} \ f^*_0 \}$ 를 따른다.

4. The Lagrange dual problem

각 $(\lambda, \nu)$ 쌍에 대해, Lagrange dual function은 최적화 문제의 optimal value $p^*$ 에 대한 lower bound를 생성한다. 그렇다면 이들 중에서 best lower bound를 찾을 수도 있지 않을까? 이는 Lagrange dual problem으로 알려져 있는 또다른 최적화 문제를 생성한다.

\begin{aligned} &\text{maximize} \quad g(\lambda, \nu) \\ &\text{subject to} \quad \lambda \succeq 0 \end{aligned}

위 문제에서 $*\lambda\succeq0,\ (\lambda,\nu)\in\mathbf{dom}\ g*$ 일 때가 **dual feasible한 상황이며, 해당 문제의 최적점인 $(\lambda^*,\nu^*)$ 를 dual optimal 혹은 optimal Lagrange multipliers라고 칭한다. 참고로 Lagrange dual problem은 최대화하려는 목표함수가 concave하고 제약조건이 convex한 컨벡스 최적화 문제이다

흔히 $\mathbf{dom}\ g=\{(\lambda,\nu)\ |\ g(\lambda,\nu)>-\infin\}$ 는 $m+p$ 보다 작은 차원을 가진다. 이때, $g$ 에 내제되어 있는 equality constraints를 식별하여 암묵적인 제약조건 $(\lambda,\nu)\in\mathbf{dom}\ g$ 을 명시적으로 표현하면 Lagrange dual problem을 더욱 간결하게 나타낼 수 있다. 예를들어 위에서 살펴본 LP의 예시에서, $A^T\nu-\lambda+c=0, \ \lambda \succeq0$ 이라는 두 개의 제약 조건은 $A^T\nu+c \succeq 0$ 으로 합쳐질 수 있을 것이다.

5. Weak and Strong duality

우리는 앞서 Lagrange dual problem을 정의하였고, 해당 문제의 optimal value인 $d^*$ 는 primal problem의 optimal value인 $p^*$ 에 대한 best lower bound가 된다. 이를 수식으로 표현해보자.

d^*\le p^*

이러한 관계는 주어진 primal problem의 convex 여부와 무관하게 (infinite한 $d^, \ p^$에 대해서도) 항상 성립하며, 이를 Weak Duality라고 칭한다. 이 두 값의 차이인 Non-negative value $p^*-d^*$ 는 optimal duality gap으로 정의되며 우리는 이 성질을 Two-way partitioning과 같은 어려운 문제에서 nontrivial lower bounds를 찾을 때 이용할 수 있다.

그렇다면 등호가 성립하는 것은 어떤 경우에서일까? 아래와 같은 Strong duality에 대해 생각해보자.

d^*= p^*

이는 Lagrange dual function에서 구한 best bound가 tight함을 의미하며, duality gap이 0인 상황이다. Strong duality는 보편적으로 성립하지는 않고 primal problem이 convex할 때 보통 성립한다. 구체적으로, convex problem에서 strong duality를 보장하는 조건을 우리는 constraint qualification이라고 부른다. 대표적인 constraint qualification 중 하나가 바로 아래의 Slater’s condition이다.

{\begin{aligned} &\text{Strong duality holds for a convex problem} \\ &{\text{minimize }} \quad f_0(x) \\[0.5ex]&{\text{subject to }} \ \ \ f_i(x) \le 0 , \ i=1,...,m \\[0.5ex]& \quad \quad \quad \quad \quad Ax = b , \\ &\text{if it is strictly feasible, } \ i.e., \\ &\exist x \in \mathbf{int}\mathcal{D}: \ f_i(x) < 0, \ i=1, ..., m, \ Ax=b\end{aligned}}

즉 inequality constraints를 strict하게 만족하는 어떤 $x$ 가 존재할 경우 (primal problem이 convex라면) strong duality가 성립한다. 참고로 첫 $k$ 개의 inequality constraints인 $f_1(x), \ ..., \ f_k(x)$ 가 affine한 경우 $\mathbf{int}\mathcal{D}$ 를 $\mathbf{relint}\mathcal{D}$ (interior relative to affine hull)로 대체하여 조건을 완화할 수 있다.

f_i(x) \leq 0, \ i=1, \ ...,\ k, \ f_i(x) < 0, \ i=k+1,\ ...,\ m, \ Ax=b

위와 같이, affine constraints는 Strict inequality를 만족하지 않아도 괜찮다.

6. Example : Mixed Strategies for matrix games

이제 예시를 하나 살펴보자. 우리는 Zero-sum matrix game의 기존 결과를 도출해내기 위해 strong duality를 사용할 것이다. 플레이어 두 명이 있을 때, 각 플레이어 A, B는 $k\in\{1,...,n\}$ , $l\in\{1,...,m\}$ 의 선택을 하게 된다. 선택 후 A는 B에게 $P_{kl}$ 을 보상을 지급해야 하며 ( $P\in\mathbf{R}^{n\times m}$ : payoff matrix) 이때 A의 목표는 이 보상을 최소화, B의 목표는 이를 최대화하는 것이 된다.

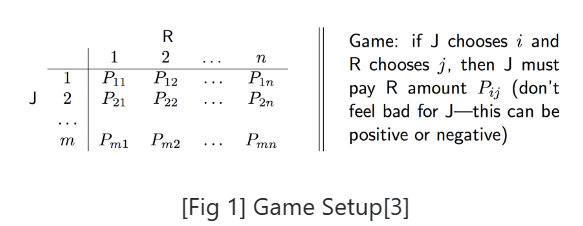
각자의 선택이 Probability distribution $\text{prob}(k=i)=u_i, \ \text{prob}(l=i)=v_i$ 를 따를 때, 보상의 기댓값은 $\sum_{k=1}^n \sum_{l=1}^m u_k v_l P_{kl}=u^TPv$ 가 된다.

첫째, A의 관점에서 분석해보자. A 전략 $u$ 를 B가 알고 있는 상황을 가정한다. B는 $u^TPv$ 를 최대화할 수 있는 다음과 같은 선택을 할 것이다.

\sup \{ u^TPv \ | \ v \succeq0, 1^Tv=1 \}= \max_{i=1, ..., m}(P^Tu)_i

따라서 A는 이러한 worst-case payoff를 최소화하는 $u$ 를 선택해야 한다.

\begin{aligned} &\text{minimize} \ \max_{i=1, ..., m}(P^Tu)_i \\ &\text{subject to} \ \ u \succeq 0, \ 1^Tu=1 \end{aligned}

이 문제에서의 optimal value를 $p^*_1$ 이라고 하자.

반대로 B의 전략 $v$ 를 A가 알고 있다면 A는 $u^TPv$ 를 최대화, B는 이를 최소화하는 전략을 취하는 것이 좋다. 이를 수식으로 표현하면 아래와 같다.

\begin{aligned} &\inf \{ u^TPv \ | \ u \succeq 0, 1^Tu=1 \} = \min_{i=1, ...,n}(Pv)_i \\ &\text{minimize} \ \max_{i=1, ..., m}(P^Tv)_i \\ &\text{subject to} \ \ v \succeq 0, \ 1^Tv=1 \end{aligned}

이 문제에서의 optimal value는 $p^*_2$ 이라고 하자.

직관적으로 상대방의 전략을 알고있는 것은 이점을 주기에, 항상 $p_1^*\ge p_2^*$ 가 성립한다고 생각할 수 있다. 이때 $p_1^*-p_2^*$ 는 상대방의 전략을 알아서 발생하는 이점으로 해석될 수 있다. 그러나 Duality를 통해 우리는 $p_1^*=p_2^*$ , 즉 mixed strategies를 사용하는 matrix game에서는 상대방의 전략을 아는 것의 이점이 없음을 증명할 수 있다. 첫 번째 케이스에 대해 다음과 같은 LP를 구성하자.