Coursera - Specialized Models: Time Series and Survival Analysis 강의의 3주차 내용을 정리한 게시물입니다.
1. ARMA Model
Autoregressive(AR)모델과 Moving Average(MA)모델을 결합한 모델로, Box-Jenkins 모델로 알려져 있기도 합니다.
AR모델은 미래의 값이 과거의 값에 의존합니다(its own past values).
MA모델은 과거의 예측 오차에 의존합니다(past forecast errors).
ARMA 모델은 ? => 둘다 고려 가능합니다
AR(p)
AR(p)모델은, 마지막 p개의 관측값에 종속됩니다. 예를 들어 p=2인 경우, 마지막 두 개 값을 반영하여 식을 다음과 같이 세울 수 있습니다.
MA(q)
MA(q)모델은, 마지막 q개의 예측오차에 종속됩니다.
우리는 각각의 가중치를 얼마로 설정할지를 추정해야 합니다.
ARMA(p,q)
p=2, q=2의 ARMA모델은 다음과 같습니다.
ARMA 모델의 특징
- 정상성을 가정합니다.
- 자기상관성을 입증하기 위해 최소 100개 이상의 관측치가 필요합니다.
ARMA모델 구현 단계
- Identification
- estimation
- evaluation
2. Determine Seasonality
- 시계열 데이터에서 계절성의 유무를 Autocorrelation Plot과 Partial Autocorrelation Plot을 활용하여 확인할 수 있습니다.
- Seasonal Subseries Plot을 통해 각기 다른 계절에 대한 평균과 분산을 파악할 수 있습니다.
- Intuition: 우리는 계절성을 근거로 미래를 직관적으로 판단할 수도 있습니다.
Seasonal Subseries Plot
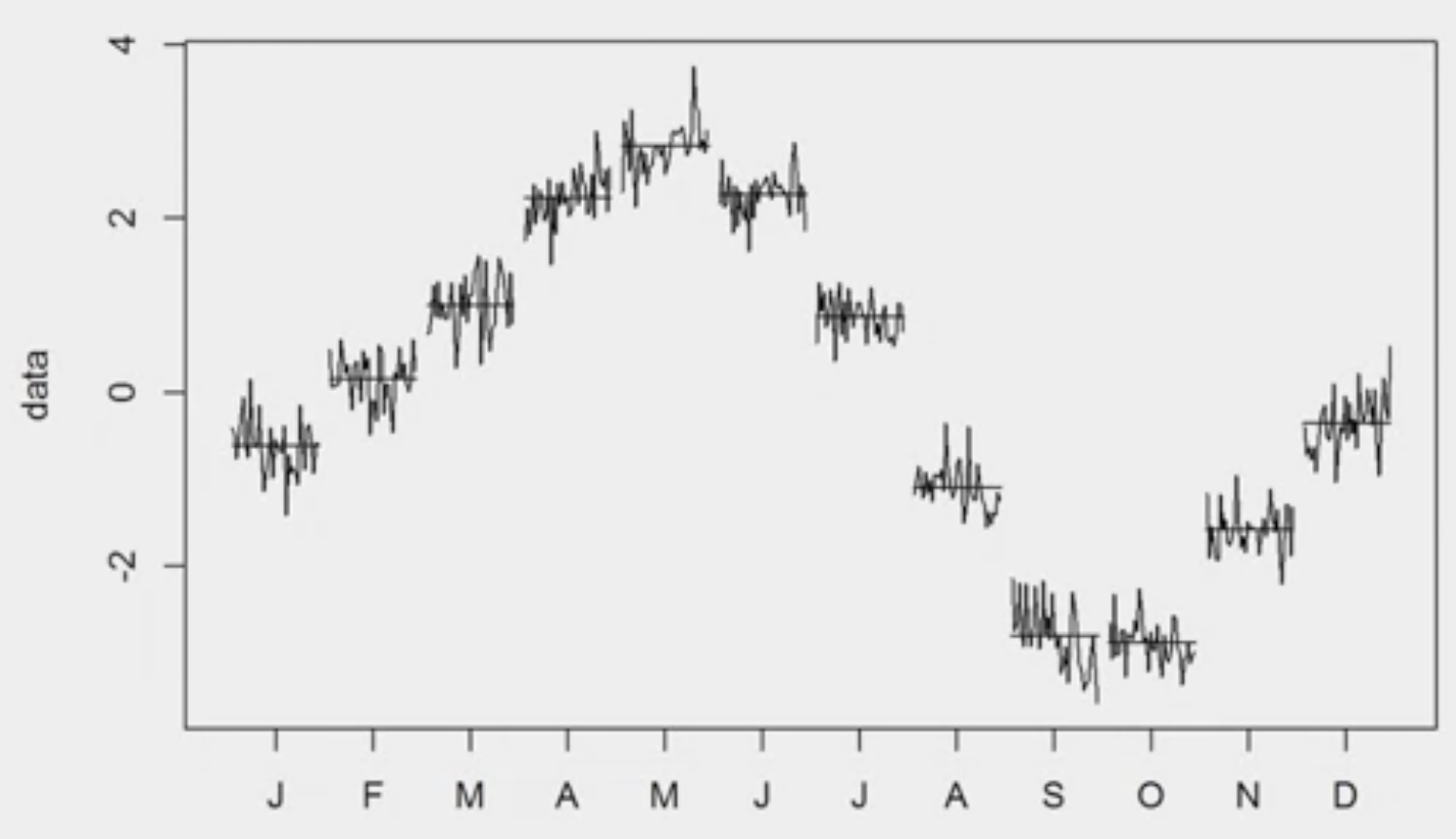
위의 그림이 하나의 계절을 월별로 분류한 그림입니다.
월별 평균 수준을 보여주고 있고(수평선), 그 주위로 실제 관측치가 표시됩니다.
Autocorrelation Function(ACF)
자기상관도(Autocorrelation) Plot
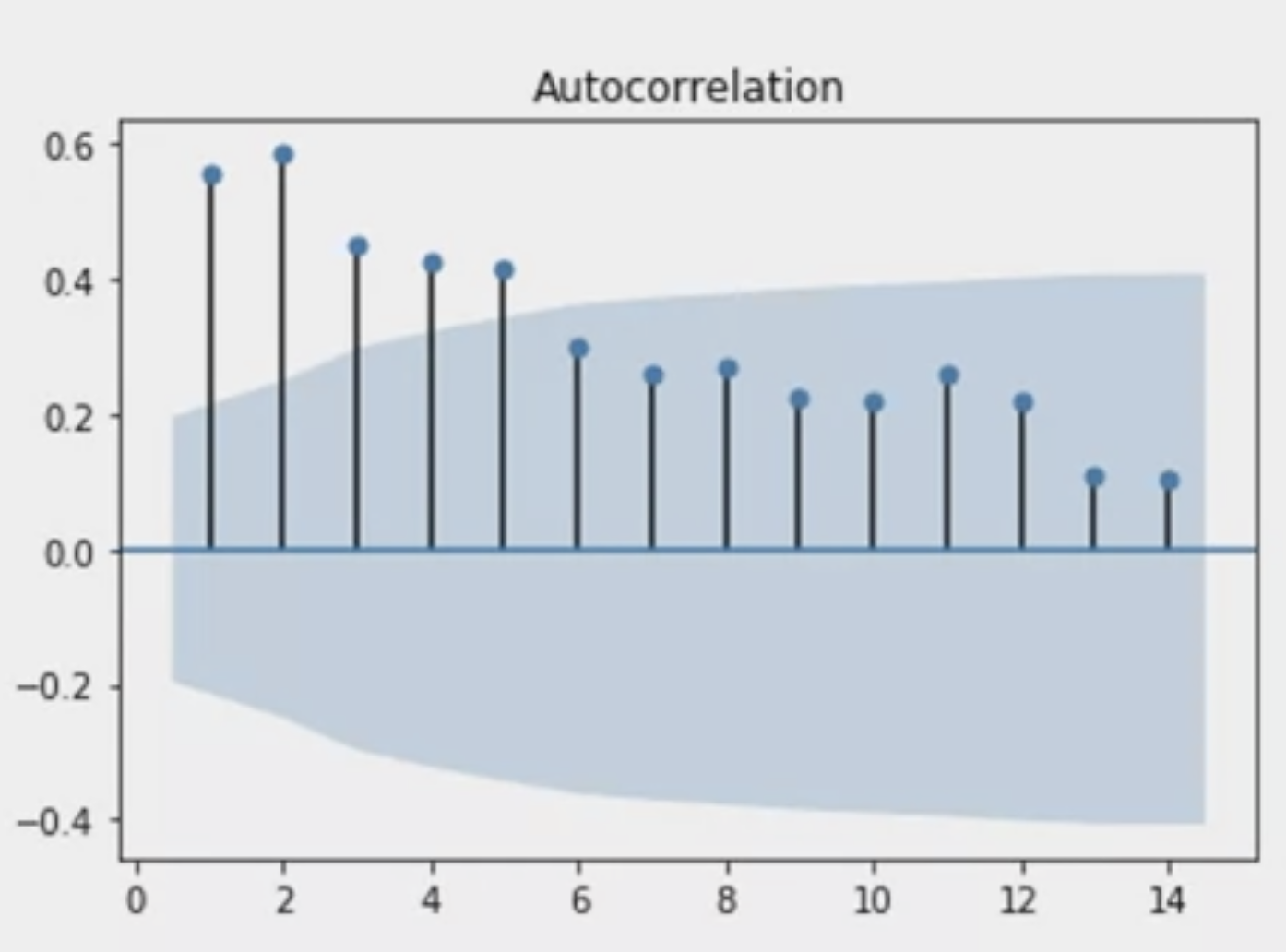
위의 플롯은 이전 관측치에 대한 의존도, 즉 특정 변수와 그 과거 값 사이의 전체 상관관계를 요약한 그래프입니다.
만약 t시점의 값이 t-1시점의 값과 관련이 있다면 t+1, t+2 .. 시점의 값도 t-1시점의 값에 영향을 받을 것입니다. 그러나 그 영향력은 점점 작아지겠죠. 이를 시각화하였다고 이해할 수 있습니다.
하지만 이 플롯만으로는 시차(lag, p)가 어떤 값인지, 1인지 5인지 등을 구별할 수 없습니다. 따라서 우리는 Partial Autocorrelation Plot을 추가로 활용합니다.
Partial Autocorrelation Function(PACF)
편자기상관도(Partial Autocorrelation) Plot
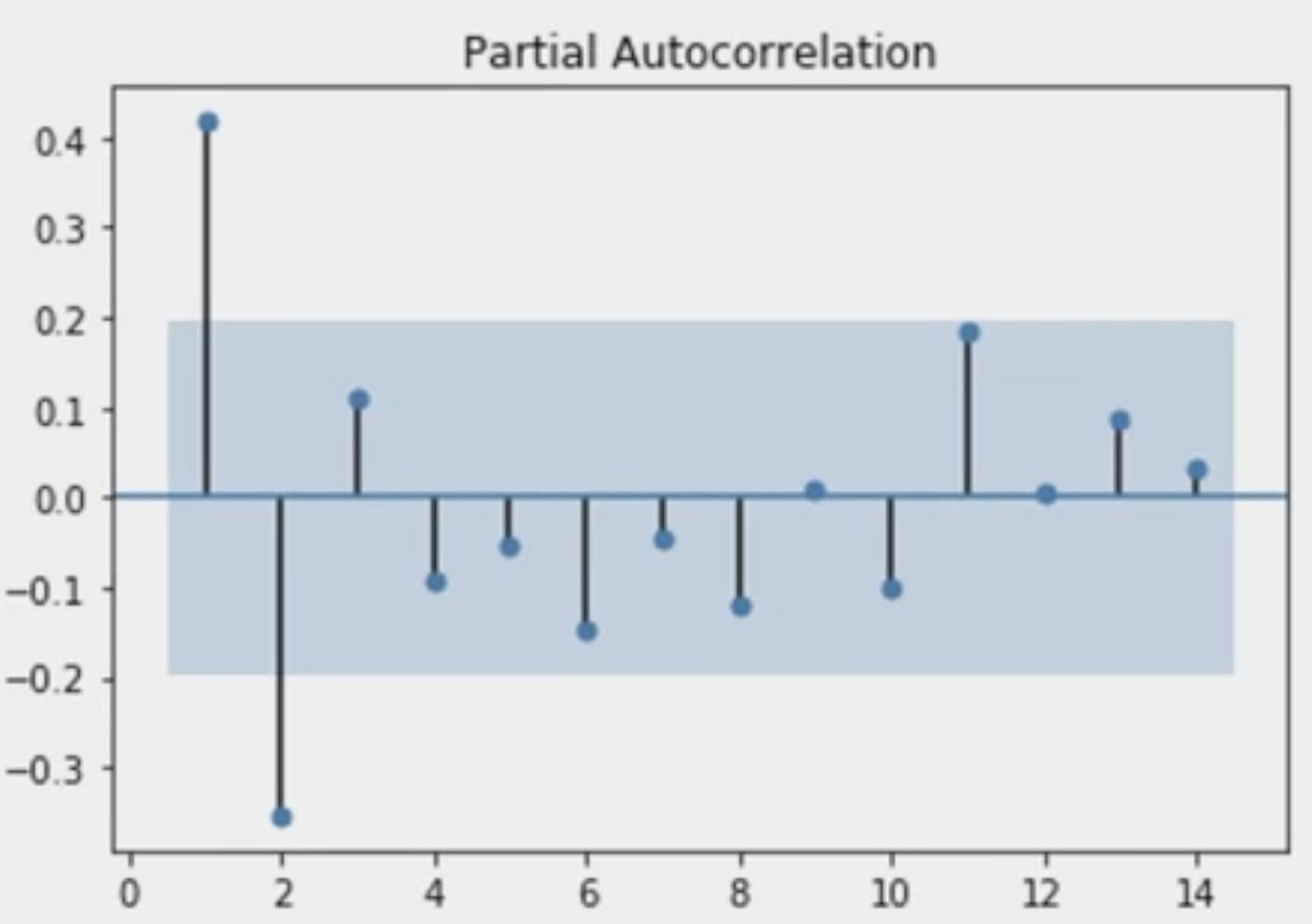
하나의 lag에 대해서만 부분적으로 자기상관도를 측정할 수 있습니다.
Parameter 결정
우선 시계열 데이터가 정상성을 가질 수 있도록 해야 합니다. 비정상 시계열 데이터는 차분 등의 방법으로 정상 시계열 데이터로 변형해주어야 합니다.
정상 시계열 데이터라는 전제를 충족하고 나면, parameter를 결정하는 방법은 두 가지가 있습니다.
1. ACF + PACF
2. p와 q를 hyperparameter로 설정 후 표준 접근법(grid search, cross validation, etc.) 적용
추가: parameter와 hyperparameter의 차이
parameter: 모델 내부에서 학습되는 변수. 주어진 데이터로부터 학습되어 모델이 새로운 데이터에 대해 예측을 수행할 때 사용됩니다.
hyperparameter: 모델의 성능, 학습 속도, 과적합 방지 등을 조절하는 변수. 모델을 만들기 전 사전에 정의됩니다.
단계
1. p값을 결정해야 합니다.
PACF 플롯에 신뢰구간을 표시합니다.(파이썬이 수행)

시차(lag) p값은 p+1시점과 그 이후의 시점의 값들에 영향을 미치지 않는 값을 선택해야 합니다.
위의 그림에서는 시점 3부터 유의미한 값이 아니라고 나오기 때문에, p값은 2로 설정할 수 있습니다.
2. q값을 결정해야 합니다.
이번에는 ACF 플롯에 신뢰구간을 표시합니다.

q값도 마찬가지로, q+1시점과 그 이후의 시점의 값들에 영향을 미치지 않는 시점을 선택해야 합니다.
일반적으로 p와 q의 차수는 너무 높지 않아야 한다고 합니다.
3. 최적화
더 최적화된 parameter를 추정하는 것은 복잡한 비선형 문제가 될 수 있습니다.
Non-linear least squares(비선형 최소제곱법)과 Maximum Likelihood Estimation(MLE, 최대우도추정)을 사용하여 접근할 수 있습니다.
평가
잔차는 가우스분포를 근사하는 백색 잡음(white noise)이어야 합니다. 따라서 잔차에도 자기상관성이나 편향이 없어야 합니다.
Guidelines for choosing AR/MA Models
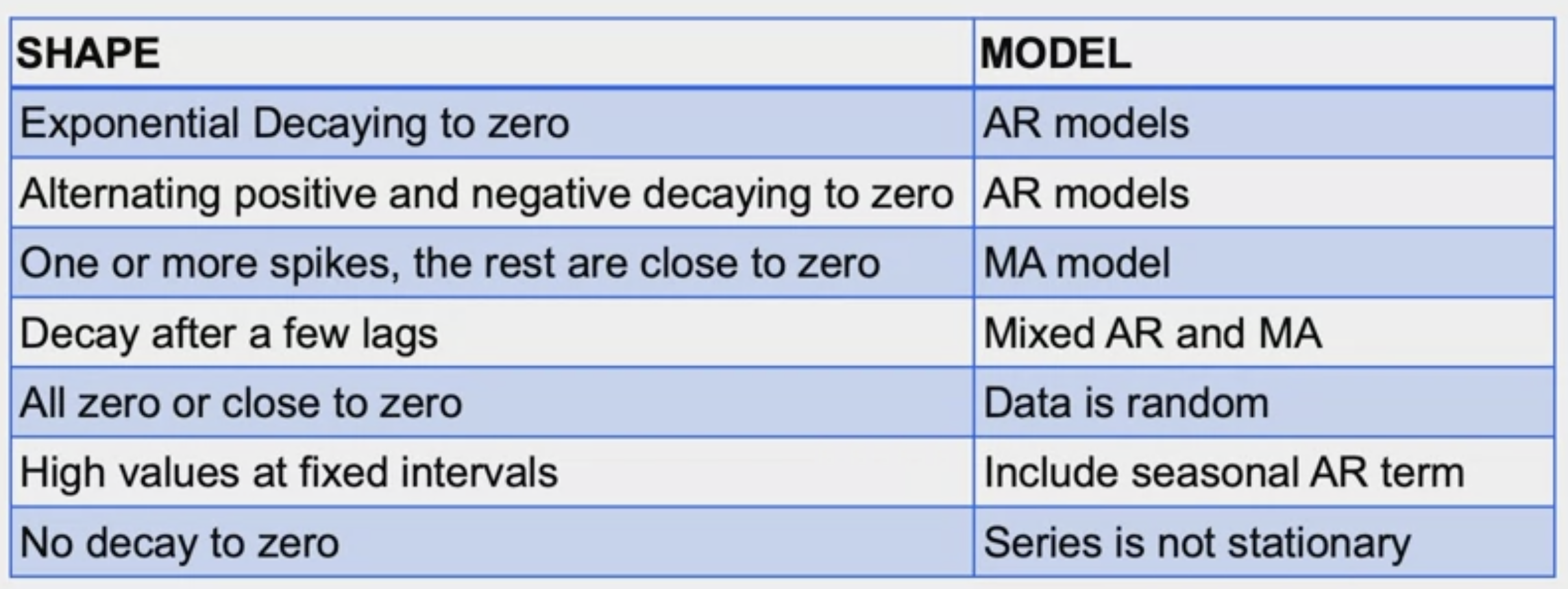
3. ARIMA & SARIMA Model
Why do we need ARIMA Model
ARIMA 모델은 비정상 시계열 데이터도 처리할 수 있다는 것이 가장 중요한 특징입니다.
ARMA 모델은 정상성을 만족하는 시계열 데이터만 다룰 수 있으나, ARIMA는 차분 과정을 통해 정상성을 만족하게 만들어줍니다.
현실 세계의 시계열 데이터는 대부분 통합적이고 복잡한, 즉 비정상성을 가지고 있을 것이기 때문에 유용합니다.
parameter
ARIMA의 구성요소는 AR, integrated component(I), MA입니다. 그리고 각각에 대응하는 parameter는 (p,d,q)입니다.
d는 차분의 횟수이며 p, d, q는 모두 양수입니다.
Differencing
차분(Differentiation)은 비정상 데이터를 정상 데이터로 바꿔주기 위한 방법입니다. 이것이 위의 구성요소 중 I에 해당합니다.
d는 시차를 뜻하며, d=1일때 다음과 같이 현재 값과 이전 값(시차 1 기준)의 차이를 계산합니다.
SARIMA
SARIMA모델은 ARIMA모델의 확장으로, 계절성까지 다룰 수 있는 모델입니다.
SARIMA(p,d,q)(P,D,Q)m 로 표현합니다. 대문자 P, D, Q는 계절성에 적용되는 parameter입니다. 예를 들어, 1년마다 반복되는 계절이라고 하면,
P: 시차 12의 값과의 자기상관도
D: 1년마다 해야 하는 차분의 횟수
Q: 시차 12의 오차항과의 상관도 라고 이해할 수 있습니다.
m이 뒤에 붙었는데, 이는 하나의 시즌을 의미합니다. 다시 말해, 계절성의 빈도입니다.
1년의 데이터에서, 분기를 하나의 계절로 생각한다면 4분기죠. 이때 m값은 4가 될 것입니다.
parameter를 선택하는 과정은 마찬가지로 ACF, PACF 플롯을 그려볼 수 있습니다. 추가적으로, 정보 기준(Information Criteria)이라는 것이 있습니다. AIC, BIC가 있는데, 이들은 모델이 사용하는 parameter 개수가 많을수록 패널티를 부여합니다. 모델이 복잡해지는 것을 방지하기 위함인데, 전체 데이터셋을 대상으로 테스트하는 데에 효과가 좋기 때문에 Train과 Test set으로 나뉘는 holdout set에서는 MSE를 사용하는게 낫다고 합니다.