Time Series Analysis and Modeling to Forecast: a Survey - 3. Linear Models

Time Series Analysis and Modeling to Forecast: a Survey

이번 게시글에서는 Linear Time Series Models를 살펴보려 합니다.
시계열의 중요 task 중 하나는 미래를 예측(predict)하는 forecasting 작업입니다.
이 prediction task는 "modeling of the relationship between past and future values of Z"를 필요로 합니다.

$Z_t$의 기본 모델은 다음의 수식과 같이 나타낼 수 있습니다.

$Z_t=f\left(Z_{t-1}, Z_{t-2}, \ldots\right)+g\left(Z_{t-1}, Z_{t-2}, \ldots\right) \epsilon_t$

where $\epsilon_t$가 i.i.d.(0,1) white noise processes, $f$ and $g^2$ are respectively the conditional mean and conditional variance of $Z_t$, that is $Z_t \mid Z_{t-1}, Z_{t-2}, . . \sim \mathcal{D}\left(f, g^2\right)$ with $\mathcal{D}$ the law of residuals. Given information from the past, f is the optimal forecast of $Z_t$ and $g^2$ is the forecast variance. This yields a forecast interval [f−g, f+g].

위의 내용을 요약해보자면 다음과 같습니다. $\epsilon_t$가 정규 분포를 따르는 white noise(백색잡음) 과정이며, $Z_t$가 이전 시간 단계의 값들에 의존하여 조건부로 평균과 분산이 결정되는 조건부 분포를 따른다는 것을 설명하고 있습니다.

f는 $Z_t$의 최적 예측치로, 과거 정보를 기반으로 계산된 조건부 평균입니다.
$g^2$는 $Z_t$의 예측된 분산으로, 과거 정보를 기반으로 계산된 조건부 분산입니다.

$Z_t$가 의존하는 조건부 분포는 $\mathcal{D}\left(f, g^2\right)$이며, $\mathcal{D}$는 잔차의 분포임을 나타냅니다. Z의 현재 값 $Z_t$가 주어진 이전 값들 $Z_{t-1}, Z_{t-2}, ...$에 대한 조건부 평균이 f이고 조건부 분산이 $g^2$인 분포를 따른다는 것입니다.

[f−g, f+g]에서, f-g는 예측치의 하한을 나타내고, f+g는 예측치의 상한을 나타냅니다. 이 예측 간격은 일반적으로 신뢰 구간으로 사용되며, 예측의 불확실성을 나타내는 데 도움이 됩니다.

---

f와 g가 선형일 때, 즉 $Z_t$와 그 과거 값 사이의 관계가 선형일 때 모델을 선형 모델이라고 하고, 그렇지 않으면 비선형 모델이라고 합니다.

선형 시계열 모델은 그 단순성과 강력한 이론적 토대 때문에 널리 사용되고 있으며, Stationarity hypothesis에 의존합니다. Wold's theorem(1938)에 의하면, 모든 정상성 과정은 오차항의 무한 가중 합(infinite weighted sum of error terms)으로 표현될 수 있다고 합니다.

가장 많이 사용되는 선형 모델로는 AR, MA, ARMA가 있습니다.
이들은 조건부 분산 $g^2$의 값은 모두 동일하게 가지고 있지만, 조건부 평균 $f$값을 다르게 가진다고 합니다.
ARMA기반 모델로는 ARIMA, SARIMA가 있습니다. 이중 SARIMA는 선형 모델이 아닙니다.

이제 모델들을 차례로 살펴보도록 하겠습니다.

---

AR, MA, ARMA는 모두 George Edward Pelham Box, Gwilym M Jenkins가 제안한 모델로, Box-Jenkins model이라고 불립니다.

ARMA모델은 아래의 두 가설에 의해 제안되었습니다.
1. 과거의 패턴이 안정적으로 지속된다면 시계열 데이터 관측치는 과거 관측치에 의해 예측될 수 있을 것이다.
=> 정상성 가정
2. 먼 과거의 관측치일수록 영향력은 줄어들 것이다.
=> 이런 상황을 고려할 수 있는 가중치를 사용해야 한다.

1. Linear Autoregressive Model - ar(p)

과거가 미래를 예측한다!
Autoregressive, 즉 "자기회귀"라는 단어에는 자기 자신에 대한 변수의 회귀라는 뜻이 있습니다. 자기회귀모델은 변수의 과거 값의 선형 결합을 이용하여 관심 있는 변수를 예측합니다. 독립변수가 이전 시점의 시계열(Lag) $[Z_{t-1}, Z_{t-2}, ..., Z_{t-p}]$이고, 종속변수가 자기 자신 $Z_t$인 모델입니다.
차수 p의 자기회귀모델 AR(p)는 다음과 같습니다.

$\epsilon_t$는 (가우스) white noise process입니다.
$Z_t$는 미래의 오차항과는 독립의 관계에 있지만, 과거의 모든 오차항과는 종속의 관계에 있다는 것을 유의해야 합니다.

$Z_t$는 임의의 정수 p에 대하여 $[Z_{t-1}, Z_{t-2}, ..., Z_{t-p}]$만의 선형결합, 즉 (t-p) 시차까지만 영향을 받는다고 설정된 모형입니다.

자기회귀모델은 다양한 종류의 시계열 패턴을 유연하게 다룰 수 있습니다. 다음은 각각 차수 1과 2의 AR모델입니다.

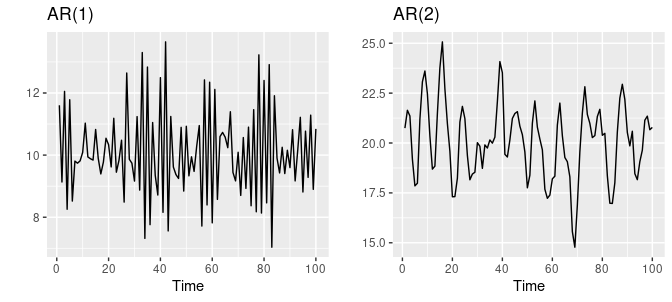
(출처: https://otexts.com/fppkr/AR.html)

$AR(1) = Z_t = \phi_0+\phi_1 Z_{t-1}+\sigma \epsilon_t$

위의 정의에 따르면 AR(1) 모델은 1 시차 전의 확률변수가 1차 자기회귀모형의 독립변수로 사용되었으며, 우리는 1차 AR모델의 계수인 $\phi_1$를 추정해야 합니다.

매개변수 $\phi$를 바꾸면 다른 시계열 패턴이 나오고, 오차항 $\epsilon_t$의 분산은 시계열의 패턴은 바꾸지 않고 눈금만 바꿉니다.

AR모델은 과거에 기반해서 미래를 예측하기엔 매우 적절하지만, 과거의 데이터와 관련이 적게 트렌드가 변동하는 경우에는 부적절하다고 합니다. 이 경우에 MA 모델을 사용할 수 있습니다.

2. Moving Average Model - $ma(q)$

과거의 충격이 현재의 결과에 영향을 준다!
MA(이동평균모델)은 과거의 시계열 값이 아닌, 과거의 오차를 이용해 회귀식을 세웁니다. 즉 과거에 예측했던 값의 오차를 통해 학습한다는 것인데, 이는 변화하는 값을 반영한다는 것이므로 이전 값 자체를 반영하는 것보다 트렌드에 민감하다고 이해할 수 있습니다.

MA모델은 시계열 $Z_t$를 그 이전 시점의 white noise process {$\alpha_t, \alpha_{t-1}, ...$}로 회귀시킨 모델로, q차 이동평균모델은 다음과 같습니다.

$\epsilon_t$는 (가우스) white noise process입니다.
종속변수는 마찬가지로 $Z_t$지만, 독립변수는 해당 시점과 그 과거의 white noise error들인 $[\epsilon_t, \epsilon_{t-1}, ..., \epsilon_{t-q}]$입니다.

3. Autoregressive Moving Average Model - $arma(p,q)$

ARMA모델은 p차 자기회귀모델 AR(p)와 q차 이동평균모델 MA(q)을 결합시킨 모델입니다.
과거의 값 자체 + 그 값의 오차값을 동시에 활용하여 현재 값을 예측하게 됩니다.

4. Autoregressive Integrated Moving Average Model - $arima(p, d, q)$

충격에도 민감하고, 과거의 값에도 영향을 받는 경우!
기존 AR, MA, ARMA 모델의 경우 데이터가 정상성을 갖추고 있어야 합니다. 따라서 비정상성을 가진 시계열 데이터의 경우는 차분(differencing)을 통해 데이터가 정상성을 갖도록 변형해주어야 합니다.
ARIMA는 ARMA모델에 차분을 d회 수행해준 모델입니다.
이 작업을 통해 비정상 데이터가 정상 데이터로 활용될 수 있습니다.

• p: AR 부분의 차수
• d: 1차 차분이 포함된 정도
• q: MA 부분의 차수
  이 차수를 찾아내기 위해 ACF, PACF를 사용하게 됩니다.

  Auto-Correlation Function(ACF)
  자기상관함수(ACF)는 $y_t$와$y_{t+k}$ 사이의 correlation을 측정하는 것입니다.
  
  
  Partial Auto-Correlation Function(PACF)
  편자기상관함수(PACF)는 ACF와 동일하게 $y_t$와$y_{t+k}$ 사이의 correlation을 측정하지만, t와 t+k 사이의 다른 y값들의 영향력(상호 선형 의존성)을 제거하고 측정합니다.

5. Seasonal Autoregressive Integrated Moving Average Model - $sarima(p, d, q)(P, D, Q)_m$

일반적인 시계열 데이터에는 추세와 계절성이 존재합니다.
추세는 차분으로 제거될 수 있지만, 계절성은 여전히 남을 수 있습니다.
ARIMA 모델은 비계절성에 대한 것이며 계절성은 별도로 처리해야 하고, 이를 위한 모델이 SARIMA입니다.