Time Series Analysis and Modeling to Forecast: a Survey

최근 연구 동향은 시계열 머신러닝, 시계열 딥러닝에 집중되어 있습니다. 하지만 통계적 시계열 분석 방법론은 여전히 중요한 위치를 차지하고 있으며, 다양한 머신러닝 기법들과 결합되어 꾸준히 사용된다고 합니다.

이 논문은 시계열 공부를 처음 시작할 때 스타트 논문으로 많이 언급됩니다. 고전적인 시계열 방법론을 다양하게 다루고 있으며, 이를 챕터별로 정리하고자 합니다. 논문의 흐름을 완전히 따라가지는 않으며, 설명된 핵심 개념을 정리할 때 모르는 개념이 있으면 같이 작성하였습니다.

그 전에 먼저 '시계열'에 대한 개념부터 알아보도록 하겠습니다.

---

시계열이란?

시계열(Time Series)이란 일정 시간 간격으로 배치된 데이터들의 수열을 말합니다.
시간 순서대로 정렬된 데이터로, 가장 보편적으로 떠올릴 수 있는 시계열 데이터는 주가 데이터가 있을 것입니다.

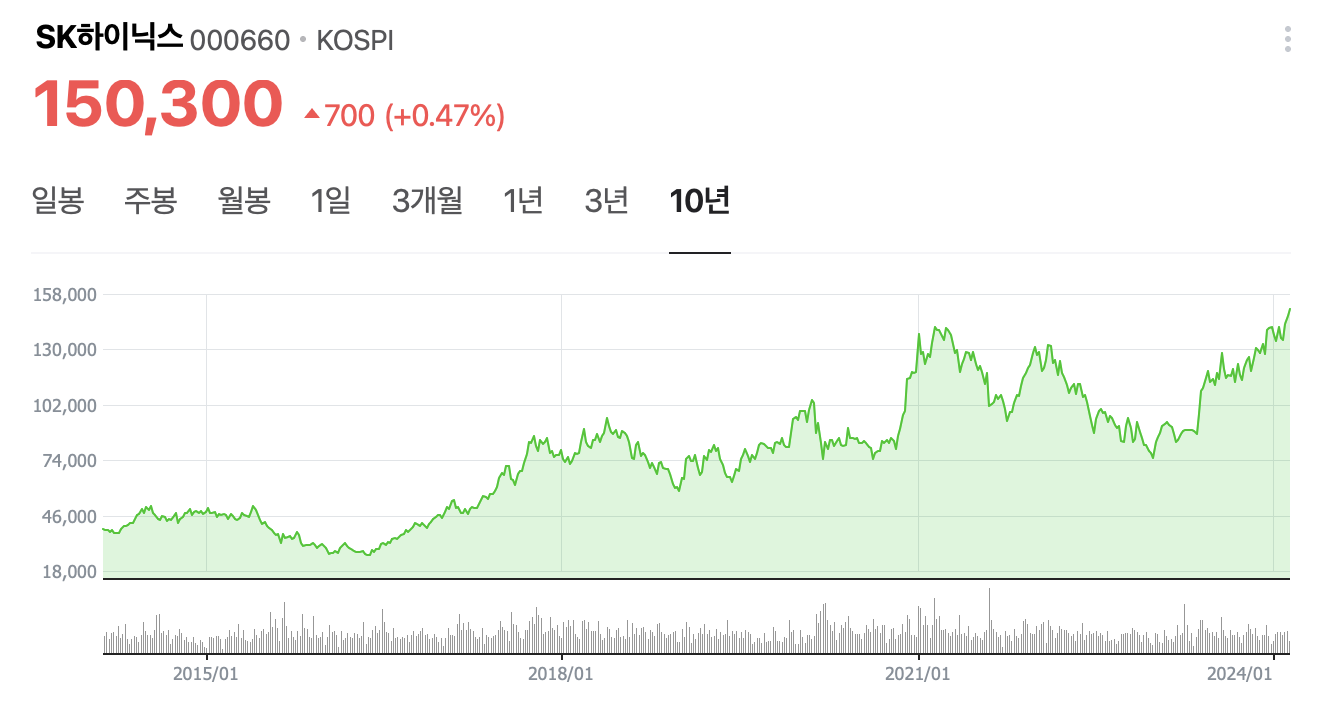
시계열 분석(Time Series Analysis)은 이 데이터를 바탕으로 여러 변수들 간의 인과관계를 분석하는 방법론입니다. 시계열 데이터에는 시간의 흐름에 따라 여러 패턴이 나타날 것이고, 이를 분석하여 미래를 예측(Forecasting)해볼 수 있습니다.
즉, 과거의 관측값을 토대로 미래의 관측값을 예측하는 것이 시계열 분석의 목적이라고 할 수 있습니다.

시계열의 구성 요소

시계열은 크게 세 가지의 요소로 구성되어 있습니다.

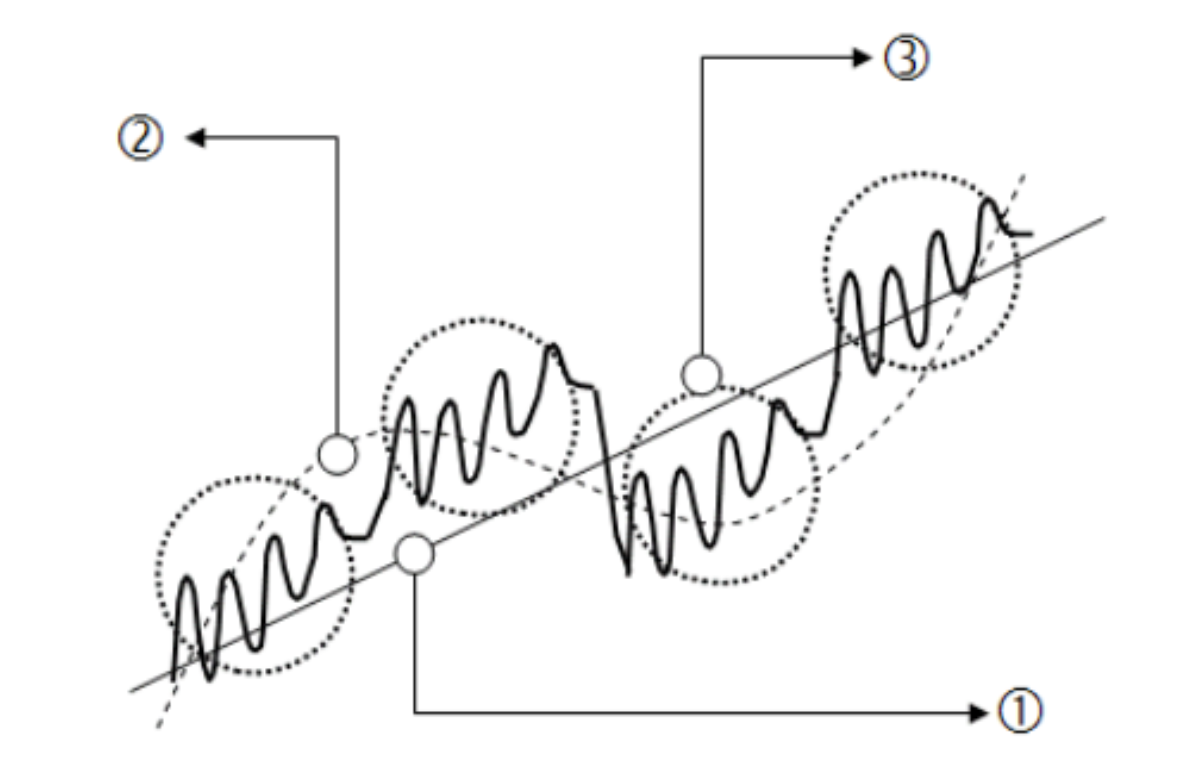
출처: https://nyamin9-data.tistory.com/102

1. 추세 (Trend)

추세는 데이터의 전반적인 경향성으로, 장기적인 증가 또는 감소의 움직임을 뜻합니다.

2. 계절성 (Seasonality)

해마다, 혹은 특정 요일 등 일정 기간 안에 반복적으로 나타나는 패턴을 뜻합니다.

3. 주기성 (Cycle)

정해지지 않은 빈도, 기간의 형태로 증가나 감소하는 경향을 말합니다.

계절성과 주기성을 혼동할 수 있는데, 계절성은 빈도가 변하지 않고 연중 어떤 시기와 관련되어 있는 패턴이고, 주기성은 일정한 빈도로 나타나지 않습니다. 일반적으로 주기들의 평균 길이는 계절성 패턴의 길이보다 깁니다.

추세를 장기변동 / 계절성을 단기변동 / 주기성을 중기변동 으로 생각하면 이해에 도움이 됩니다.

이외에도 측정 및 예측이 어려운 불규칙성이 존재합니다. 잡음(noise)이라고도 불리는 이 요인은 추세와 계절성을 기반으로 예측하기가 어렵습니다.

---

확률과정 (Stochastic Process)

확률과정은 시계열 데이터와 밀접한 연관성이 있습니다.
시계열 데이터는 대부분의 경우 확률과정 모형을 따릅니다.
확률과정이란, 확률법칙에 의해 생성되는 일련의 통계적 현상을 말합니다.

t가 시간이면, 이 $\{Z_t\}$를 시계열과정 또는 시계열모형이라 합니다.
$\{Z_t\}$는 시점 t에서의 확률변수를 나타내고, $\{z_t\}$는 그 실현값입니다. 각 시점마다 실현값이 존재합니다.

$\{Z_t, t∈T\}$ => $\{z_1, z_2, z_3, ..., z_n\}$

관측되는 시계열 자료도 실현값들의 집합이며, 이를 토대로 확률과정을 추정해 내는 것입니다.

각 시점에 따라 사건의 확률분포가 달라진다고 이해

---

정상성 (Stationarity)

시계열은 시간의 흐름에 따라 나열된 데이터입니다. 따라서 '시간'이라는 요소에 많은 영향을 받게 되는데요, 정상성은 이와 관련된 시계열의 특성 중 하나라고 볼 수 있습니다. 정상성은 시계열 분석에서 중요한 가정 중 하나입니다.

정상성(Stationarity)이란?

정상성은 "시간에 상관없이 일정한 성질"을 뜻합니다.
논문에서는 "if its statistical properties are time-independent"라고 표현하고 있습니다.
정상성을 나타내는 시계열 데이터라 함은, 해당 데이터의 특징이 관측된 시간과 무관하게 나타난다는 것을 말합니다. 관측 시점과 상관이 없고, 어떤 시점에서 보더라도 같은 분석 결과가 나올 것입니다.
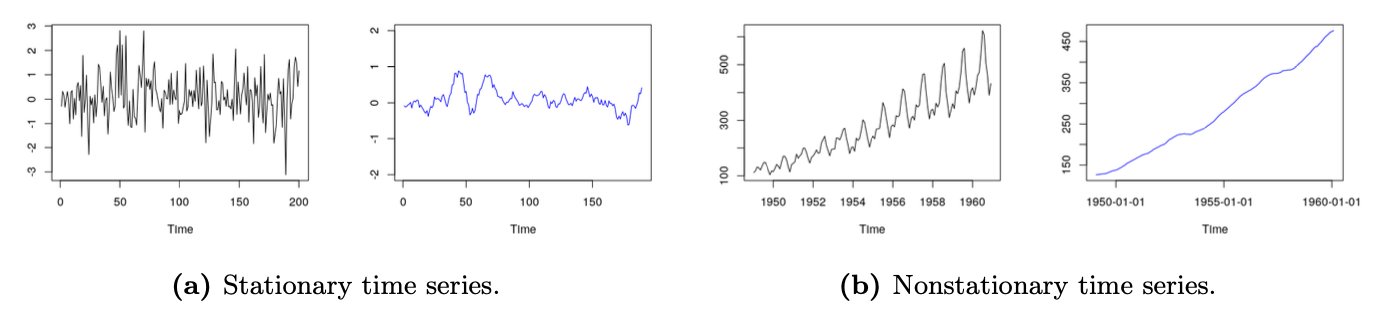
정상성을 나타내는 시계열은 장기적으로 볼 때 예측할 수 있는 패턴을 나타내지 않습니다.

추세나 계절성이 있는 시계열은 정상성을 나타내는 시계열이 아닙니다. 추세와 계절성은 서로 다른 시간에 시계열의 값에 영향을 주기 때문입니다.

정상시계열은 자료 변화의 폭이 일정하며 시간에 따라 상이한 자기상관적(서로 다른 두 시점에서의 관측치 사이에 나타나는 상관성) 패턴을 나타내는 구간이 없습니다.

정상성은 강정상성과 약정상성으로 나눌 수 있습니다.

Strong Stationarity

$\{Z_t, t\geq1\}$ 에 대해서 임의의 자연수 t_1, ..., t_n에 대하여 결합확률밀도함수 f가 다음을 만족할 때, $\{Z_t\}$를 강정상성을 띤다고 말합니다.

$f(Z_{t_1},Z_{t_2},...,Z_{t_n})=f(Z_{t_1+k},...,Z_{t_n+k})$

확률과정이 각 시점마다 사건의 확률분포가 존재한다고 했는데, 강정상성을 띠게 된다면 매 시점마다 특정 사건이 발생할 확률의 분포가 동일한 것입니다.
이러한 강정상성을 충족하는 데이터는 현실에서는 희박합니다.

Weak Stationarity

약정상성은 강정상성보다는 약하지만, 이 역시 시계열 데이터가 시간에 따라 일정한 특성을 유지하는 것을 의미합니다.

시계열 $\{Z_t, t\geq1\}$에서

1. 모든 t에 대하여 $E(Z_t) = \mu ∈R$
   -> $Z_t$의 기대값이 시간에 따라 변하지 않습니다. 즉 시간이 변해도 시계열 데이터의 평균은 일정합니다.

2. 모든 t, s에 대하여 $Cov(Z_t, Z_s)=Var(Z_t)=\sigma ^2 ∈ R< ∞$ for t=s
   -> $Z_t$의 분산이 시간에 따라 변하지 않습니다. 시간 t에 비종속하며 유한합니다.

공분산과 분산이 동일한 값으로 측정되는데, 이는 시계열 데이터에서 자기공분산(/자기상관: 특정 시점의 데이터가 자기 자신과의 관계에서 가지는 변동성)을 의미합니다. 즉, 같은 시점(t=s)에서의 데이터의 변동성을 측정하고 있으며, 그것이 같다는 것은 변동성이 일정하다는 것을 의미합니다.

3. 모든 t, s, h에 대하여 $Cov(Z_t, Z_s) = Cov(Z_{t+h}, Z_{s+h})$ for t!=s
   -> 시간 불변성(time invariant property)이라 합니다. 같은 시간 간격 h만큼 시점을 이동(시간 변화)해도, 공분산이 변하지 않는다는 것을 의미합니다.
   
   

---

왼쪽이 정상성을 나타내는 시계열 데이터, 오른쪽이 정상성을 갖지 않는 시계열 데이터입니다. 시계열 데이터가 시간의 흐름에 영향을 받지 않는 모습을 확인하실 수 있습니다.