[paper review] Time Series Analysis and Modeling to Forecast: a Survey - 2. Decomposition

Time Series Analysis and Modeling to Forecast: a Survey

시계열 분해(Time Series Decomposition)란

시계열 분해란, 시계열 데이터의 성분(추세/계절성/주기성/불규칙성)들을 분해하는 것입니다. 분해법이란 이렇게 분해된 각 성분을 개별적으로 예측한 후에 이를 다시 결합시켜서 예측하는 방법입니다. 시계열 데이터의 성분 중 추세, 계절성, 주기성이 '체계적 성분'으로 구분되며, 분해 대상입니다.(불규칙성은 분해 대상이 아닙니다)

기본적으로 시계열 데이터는 Autoregressive, 즉 자기상관성을 전제로 합니다. 이는 미래의 데이터가 과거의 데이터에 영향을 받는다는 성질로, 어떻게 영향을 받는지를 알아내는 것이 시계열 분석에서 가장 중요한 일이 됩니다. 하지만 이를 여러 요소가 합쳐진 raw data로 분석하기는 어렵기 때문에, 알려진 변동 요인들을 제거, 즉 분리해 냄으로써 시계열 모델의 예측 성능을 향상시킬 수 있습니다.

시계열 분해 방법

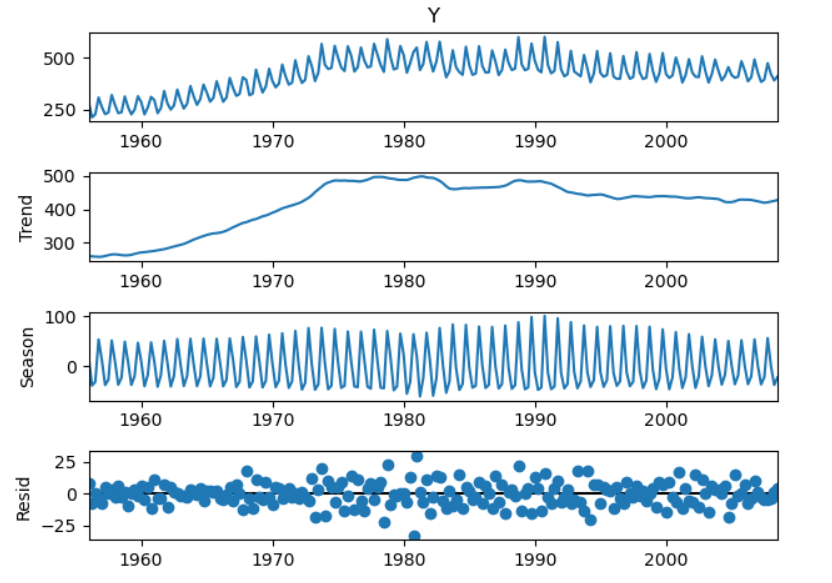
일반적으로, 시계열 데이터를 분해하는 방법은 3단계로 구분할 수 있습니다.

1. 추세를 분해합니다.
2. 원래 데이터에서 추세를 제거한 후 기간별 데이터의 평균을 구합니다. 이 값이 계절성 요인입니다.
   예를 들어 데이터의 기간이 2010~2020년도의 월별 데이터라고 하면, 1월/2월/.../12월 평균값들이 계절성 데이터가 될 것입니다.
3. 원래 데이터에서 추세+계절성을 제거하여 잔차값을 구합니다.
   2번에서 제거한 계절성은 평균값이기 때문에 실제 데이터와는 차이가 생기게 됩니다.
   따라서 그 차이가 얼마인지 잔차(원래 데이터-추세-계절성)를 구해줘야 합니다.

결국 추세를 분해하는 방법에 따라 계절성과 잔차값이 결정됩니다.

추세를 분해하는 방법으로는

• 고전적인 분해법(가법 분해, 승법 분해)
• 평활법 - 이동평균(Moving Average)법, 지수평활법 ..

등이 있습니다.

고전적인 분해법

T, S, C, I는 각각 추세, 계절성, 주기성, 불규칙성을 나타냅니다.

가법 분해(Additive Model)

주로 계절성분의 진폭이 시계열의 수준에 관계없이 일정한 수준일 때 사용합니다.

승법 분해(Multiplicative Model)

계절성분의 진폭이 시계열의 수준에 따라 변동할 때 사용합니다.

위의 식에 로그를 씌워서 로그가법모형으로 변형할 수 있습니다. 로그를 씌우면 단위가 큰 데이터의 스케일링(scaling)효과도 있고, 곱셈 연산은 로그를 씌우면 덧셈 연산으로 바뀌기 때문에 연산량이 줄어듭니다.

이외에 유사 가법 분해(Psuedo-Additive Model)가 있습니다. 이는 승법 분해시 값이 0이면 전체 시계열 데이터가 0으로 소멸되는 경우를 방지하기 위해 가법 분해와 승법 분해를 혼합한 방법입니다.

평활법

과거 및 현재 자료의 불규칙 변동을 부드럽게 평활(smoothing)시켜 미래의 값을 예측하는 기법입니다. 자료들 간의 상관관계를 고려하지 않은 예측기법입니다.

이동평균(Moving Average)

전체 시계열 데이터를 대상으로 일정기간별 평균을 구하는 방법입니다.
기간별로 데이터 위를 이동하면서 평균을 구한다고 직관적으로 이해할 수 있습니다.
이동평균법을 적용하면 전체 데이터 수가 줄어듭니다.

이동평균을 구하게 되면 요소의 값은 다음과 같이 구할 수 있습니다.

• 추세 = 이동평균
• 계절성 = 자료값/이동평균
• 잔차 = 관측값/예측값
  • 예측값 = 이동평균 * 계절성

1. 단순이동평균(Simple moving average)
   추세/계절성이 없는 수평적 패턴을 가진 시계열 데이터에 적용합니다.

   $M A_n=\frac{Z_n+Z_{n-1}+\cdots+Z_{n-m+1}}{m}=\frac{1}{m} \sum_{t=n-m+1}^n Z_t$

   (m=기간, n=시점)
   데이터의 변동이 클수록 최근 데이터의 영향을 많이 받아야 하므로 m이 짧은 것이 좋습니다.
   m은 MSE(Mean Squared Error)가 가장 작은 값을 갖도록 선택합니다.

   $\operatorname{MSE}(m)=\frac{1}{n} \sum_1^n\left(Z_t-F_t\right)^2$

2. 이중이동평균법(Double moving average)
   추세 패턴을 가진 시계열 데이터에 적용합니다.
   선형추세가 있는 시계열을 단순이동평균으로 계산 시 추세를 늦게 따라가며 동시에 체계적 오차가 발생합니다. 이를 보완하기 위한 방법이 이동평균을 두 번 적용한 이중이동평균법입니다.

   $M A_n^{\prime}=\frac{1}{m}\left(M A_n+M A_{n-1}+\cdots+M A_{n-m+1}\right)$

지수평활법(Exponential Smoothing)

모든 관측치에 동일한 가중치를 부여하는 이동평균법과 달리 전체 데이터를 사용하되 가장 최근 데이터에 큰 가중치가 주어지고 과거로 갈수록 가중치가 기하학적으로 감소되는 가중치 이동평균 예측 기법의 하나입니다.

1. 단순지수평활법
   수평적 패턴의 데이터에 적용합니다.
   $S_n=\alpha Z_n+\alpha(1-\alpha) Z_{n-1}+\alpha(1-\alpha)^2 Z_{n-2}+\cdots$
   n=시점, $(0\leq \alpha \leq 1)$
   α는 단순지수평활상수로, MSE를 가장 작게 하는 값으로 선택합니다.

시계열 {$Z_n$}의 시점 n+1에서의 지수평활치

시계열 {$Z_n$}의 시점 n+1에서의 예측치

2. 이중지수평활법
   추세 패턴을 가진 데이터에 적용합니다.

   $S M_n=\alpha Z_n^{\prime}+(1-\alpha) S M_{n-1}^{\prime} \\ S M_n^{\prime}=\alpha S M_n+(1-\alpha) S M_n^{\prime}$

   지수평활을 두 번 처리해줍니다!

3. 삼중지수평활법
   추세+계절성 패턴을 가진 데이터에 적용합니다.

위의 분해법들을 식으로 이해하기보다는 개념만 이해해도 충분할 것 같습니다!