통계방법론 W4 - Hypothesis Testing

통계학에서 가설이란, claim or statement about a population parameter, 즉 모수에 대한 주장이다.

Hypothesis Testing

통계학에서 가설검정이란, 그 주장이 옳은지 틀린지를 표본자료를 이용해 판단하는 것이다.

• 귀무가설, Null hypothesis, $H_0$
  • 현재 상태; 지금이 맞다.
• 대립가설, Alternative hypothesis, $H_\alpha$
  • 지금은 틀렸고 새로운 이론이 맞다. 귀무가설의 보완.

한 가설이 거짓이면 다른 한 가설은 참이어야 한다.

가설설정 규칙

• 귀무가설은 모수를 특정한 값으로 표현한다. written in $\mu = k$ form
  ex1. Is the mean of the population less than 40?
  $H_0: \mu = 40$
  $H_\alpha: \mu < 40$
  ex2. Is the population proportion greater than 0.18?
  $H_0: p = 0.18$
  $H_\alpha: p > 0.18$
  ex3. Has the population mean changed from 12?
  $H_0: \mu = 12$
  $H_\alpha: \mu \ne 12$
• 대립가설은 귀무가설에서 지적한 모수의 값이 아닌 어떤 영역으로 나타내는데, 양쪽으로 다 고려하는 양측검정과 한쪽만 고려하는 단측검정이 있다.

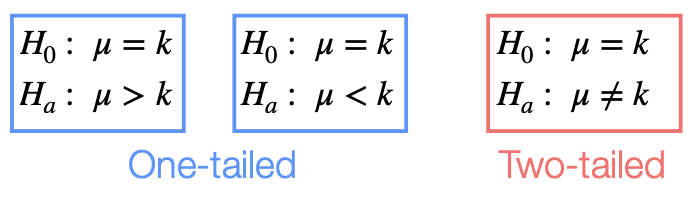
• One-tailed: 단측검정. 대립가설이 한쪽만으로 나타남
• Two-tailed: 양측검정. 대립가설이 양쪽으로 나타남

가설검정 결과

• Reject the null hypothesis
• Fail to reject(=Accept) the null hypothesis

H0을 Reject하기 위해서는 얼마나 달라야 하는가?
-> 유의수준에 따른 기각역에 속해야 한다.

Type I error vs Type II error

Type I error (=False Positive)

• Rejecting a true null hypothesis
  제 1종 오류. 귀무가설이 맞는데도(Positive) 잘못하여(False) 이를 기각함.
• 제 1종 오류가 발생할 확률 $\alpha$
  • 검정의 유의수준(significance level)이라고 한다.

Type II error (=False Negative)

• Failing to reject a false null hypothesis
  제 2종 오류. 귀무가설이 거짓이고(Negative) 대립가설이 사실임에도 불구하고 귀무가설을 기각하지 못함(False).
• 제 2종 오류가 발생할 확률 $\beta$

일반적으로 $\alpha$와 $\beta$는 반비례 관계이다.
표본의 수를 크게 하면 $\alpha$와 $\beta$의 크기를 동시에 줄일 수 있다.

Power of the test(= $1-\beta$)

Probability of a statistical test rejecting H0, when H0 is false
검정력; 귀무가설이 거짓일 때 귀무가설을 기각할 확률

Interpretation

Failing to reject the null hypothesis does not mean that the null hypothesis is accepted as true. It simply means that there is not enough evidence to reject the null hypothesis. (or support)

Hypothesis Testing: Population Mean Given $\sigma$

use z statistic

계산순서

Step 1. 가설 설정

모평균이 98,500이 맞는지 틀린지 검정

Step 2. 어떤 통계량 쓸건지 결정

모분산을 알고 있으니 z통계량을 쓴다.

Step 3. 유의수준을 결정한다.

이 문제에 대해서는, $\alpha=0.05$로 설정한다.

Step 4. Decision Rule을 설정한다.

양측검정이고 양쪽 꼬리에 0.025 만큼의 기각역이 있으며 임계값 z는 +-1.96일 것.
Decision rule: Reject H0 if the data produce z>1.96 or z<-1.96

Step 5. 표본의 통계량 확인

이 문제에서

• 표본의 개수는 112개
• 표본평균은 102,220
• 모분산은 14,530

Step 6. Analyze the data

Step 7. Reach a statistical conclusion

Since the test statistic (or “observed value”), z = 2.71, is greater than the critical value of 1.96, reject H0

Step 8: Interpret the Result and Make Decision

• For a company, CPAs will be more expensive to hire
• For new accountants, it may mean the potential for greater earning power

정리
1. 가설 및 유의수준 설정 후,
2. 유의수준에 맞는 z임계값을 구한다.
3. 주어진 통계량을 활용해서 구한 z값이 임계값 미만/초과(양측검정)일 시에 귀무가설을 기각한다.

p-value

the probability of getting a test statistic at least as extreme as the observed test statistic computed under the assumption that the null hypothesis is true

귀무가설이 사실이라고 가정하고 계산한, 표본에서 나온 결과보다 더 극단적으로 나올 확률값이다. 귀무가설을 검정하는 또 하나의 방법이다. 관측유의수준(observed significance level)이라고도 불린다.

p값은 귀무가설이 기각되는 유의수준의 최솟값을 정의해준다 !
ex. using this p-value, the null hypothesis could be rejected at α = 0.00001
유의수준이 0.00001일때부터 쭉 - 기각된다는 소리 ..

$\alpha$값과 p값을 비교하면 가설을 검정할 수 있다.
p값이 작게 나올수록 H0을 기각하여야 한다는 결론이 나온다.
유의수준이 0.05일 경우, "p값이 0.05보다 작으므로 유의하다(귀무가설을 기각한다)." 라는 결론이 나온다.

단측검정

• p값을 구하는 방법
  단측검정에서, 만약 step 6의 z값이 2.04로 나왔다고 가정해보자.
  2.04에 해당하는 확률은 0.4793 (z분포표)
  0.5 - 0.4793 = 0.0207
  p값은 0.0207
• p값 vs. $\alpha$
  • $p-value < \alpha$ → reject H0
  • $p-value \geq \alpha$ → do not reject H0
  쉽게 말해서, p값이 0.0207이면 한 쪽 꼬리의 0.0207 만큼의 구간이 해당하게 되는데 이것이 위에서 말한 "귀무가설이 사실일 확률"이라고 이해하면 된다. 귀무가설이 사실일 확률이 매우 작기 때문에(유의수준보다 작다) 귀무가설을 기각할 수 있는 것이다.
  기각역과 헷갈리지 않도록 유의한다.

양측검정
양측검정에서, p값은 $\alpha/2$와 비교된다.
p값을 구하는 방법
단측검정에서, 만약 step 6의 z값이 2.71로 나왔다고 가정해보자.
2.04에 해당하는 확률은 0.4966 (z분포표)
0.5 - 0.4966 = 0.0034
p값은 0.0034

• p값 vs. $\alpha/2$
  • $p-value < \alpha/2$ → reject H0
  • $p-value \geq \alpha/2$ → do not reject H0
  p값이 0.025보다 작기 때문에 H0을 기각한다.

Critical Value Method

기각역을 결정하는 z임계값이라고 이해할 수 있다.

임계값이 얼마인지를 계산한다면 [95,809보다 작거나 101,191보다 높은 값을 가지면 귀무가설 기각] 이라는 결론을 얻을 수 있고, 표본평균이 102,200 즉 임계값보다 높은 값을 가졌기 때문에 기각한다.

Hypothesis Testing: Population Mean When $\sigma$ Unknown

use t statistic

아까 z값으로 표준화하는 식에서, 시그마 값만 s값으로 대체하면 된다.
자유도가 n-1이라는 것을 유의!

Hypothesis Testing: Population Proportion

use z statistic / rule of thumb for CLT

recall: rule of thumb for the CLT : $np \geq 5, nq \geq 5$
Step 1. Establish the hypothesis
Step 2. Determine the appropriate statistical test
np = (200)(0.08) = 16, nq = (200)(0.92) = 184
-> Central Limit Theorem holds
use z statistic
Step 6. Analyze the data

나머지는 같다.

Hypothesis Testing: Population Variance

use chi-square statistic

나머지는 같다.

Solving for Type II Errors

만약 귀무가설이 기각되지 않았다면, 올바른 의사결정 or Type II Error일 것이다.
현실에서 Type II Error는 사업에서 기회를 놓치거나 생산품 퀄리티 하락 등 문제를 발생시키기 때문에 중요하다.

Type II Error는, 귀무가설이 거짓인데 기각하지 않은 오류이다.(대립가설이 참)

Type II Error의 확률

예를 들어 보자.
$H_0 : \mu=12$
$H_\alpha : \mu < 12$
만약 귀무가설이 기각된다면, 실제 모평균의 값은 무엇일까?
11.99일까 11.90일까 11.5일까 10일까?
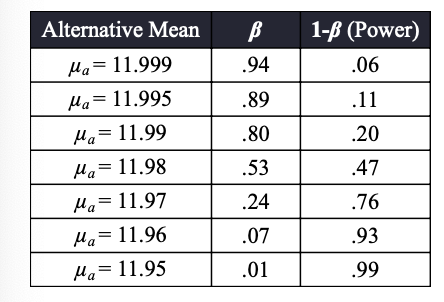
각 alternative value(11.99, 11.90, ...)는 각각 다른 Type II error의 확률을 가질 것이다.

n=60
$\bar x$=11.985
$\sigma$=0.10

$\alpha$=0.05일 때 z값은 -1.645

-1.645보다 -1.16이 작지 않기 때문에 기각역에 속하지 않는다. 즉, 귀무가설이 기각되지 않는다.
하지만, 만약 모평균이 11.99라면 귀무가설은 거짓인 것이다.

Solving for Type II Errors

Step 1. 유의수준 하의 임계값을 계산

$\alpha$=0.05
원래 문제에서 주어진 귀무가설의 값을 $\mu$로 두고 계산한다.

Step 2. Alternative value 대입 후 임계값 계산

Alternative value를 11.99라고 하고 임계값을 다시 계산해본다.

Step 3. Type II Error Probability

step2를 계산해서 나온 임계값 z의 값을 z분포표에서 찾아 그 확률을 구해보면, $\operatorname{Pr}\left(z_1 \geq-0.85\right)=0.8023=\beta$의 값이 나온다.
해당 z값보다 큰 값이 오류의 확률이라고 생각한다.
-> 0.8023 is the probability of failing to reject the hypothesis that the mean is 12 when the actual mean is 11.99.

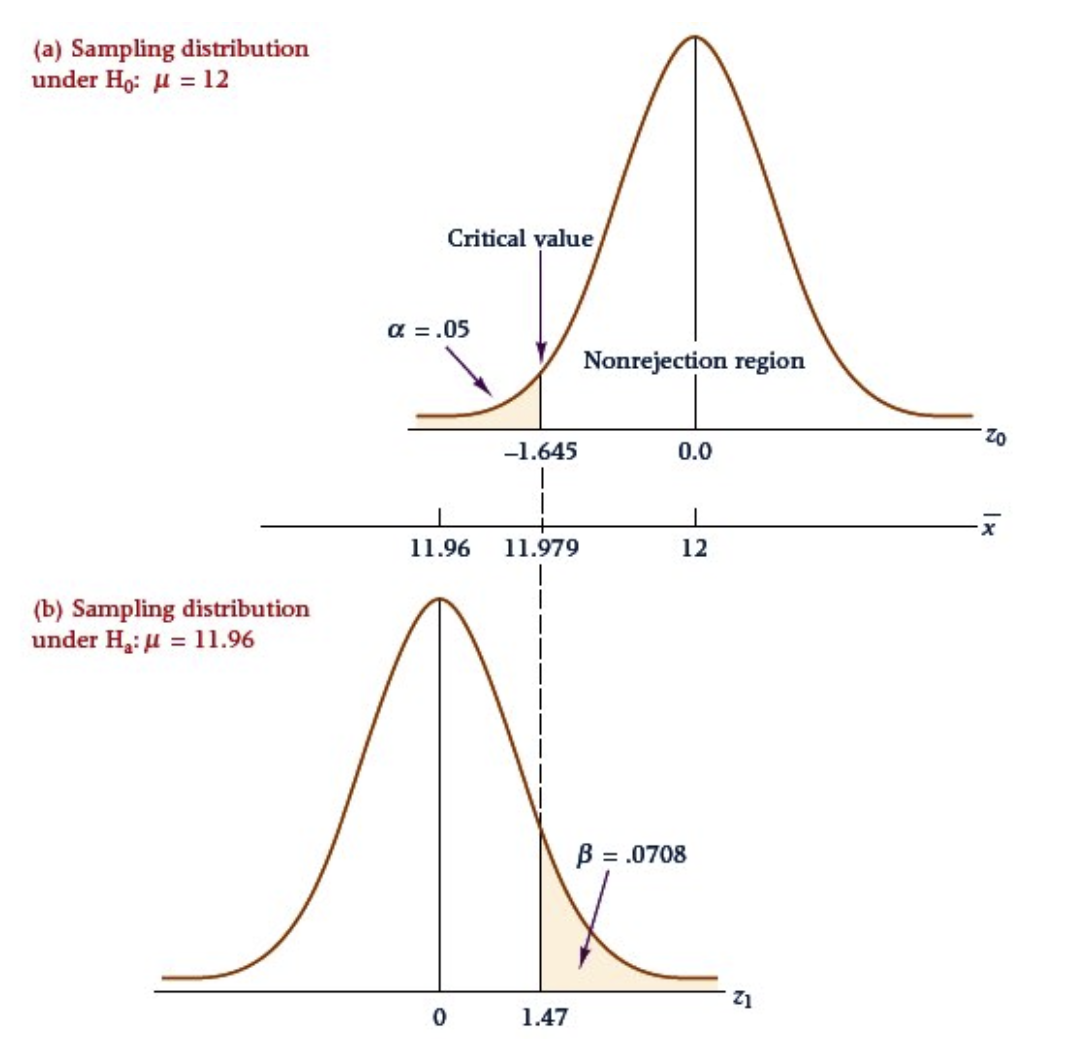
Step 4. 검정력(Power)

$1-\beta$값으로 Power를 구할 수 있다.

Effect of Increasing Sample Size

Increasing the sample size decreases the value of the standard error, and the critical value changes.

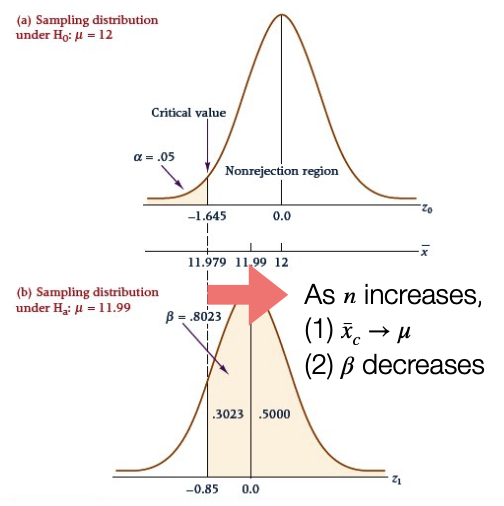
• 표본의 크기가 커질수록,
  • 표준오차의 값이 줄어들고 임계값이 변한다.
  • 표본평균은 모평균에 가까워진다.
  • $\alpha, \beta$ 값을 동시에 낮출 수 있다. 즉, Type-I Error와 Type-II Error를 동시에 낮출 수 있다.