프로그래머스 문제 - 최적의 행렬 곱셈

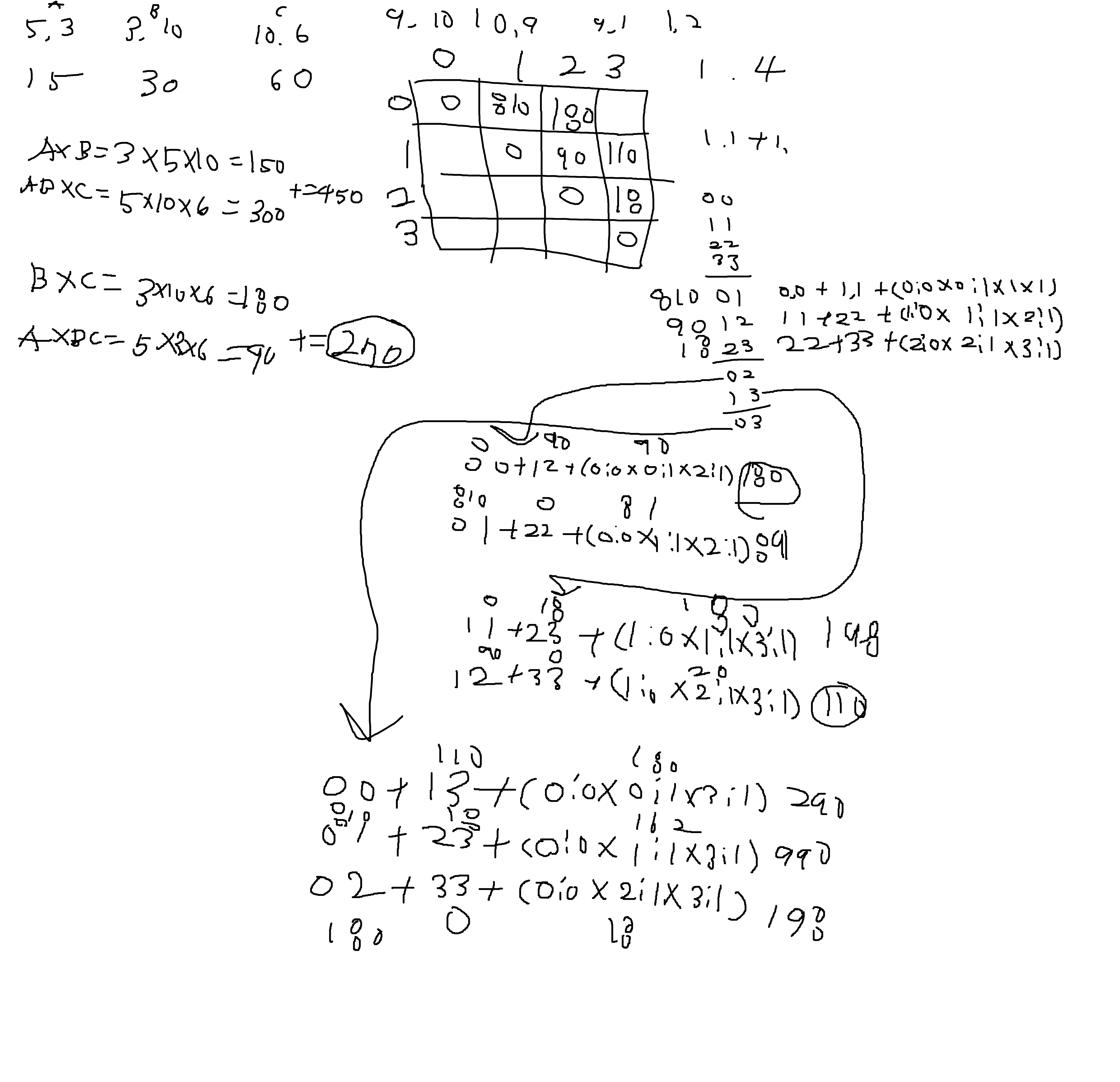
프로그래머스 최적의 행렬 곱셈 문제 풀이를 진행하였습니다.

문제 해석

문제를 읽으면 아래와 같은 해석이 가능합니다.

크기가 a by b인 행렬과 b by c인 행렬이 있을 때 두 행렬을 곱하기 위해서는 a * b * c번 곱해야합니다.
행렬이 3개 이상일 경우 연산 순서에 따라 곱하기 연산의 횟수가 달라질 수 있습니다.
주어진 행렬을 가지고 최소의 연산 횟수를 구해야합니다.

문제 풀이

이 문제는 연쇄행렬 최소곱셈 알고리즘을 알고 있어야 문제를 쉽게 해결할 수 있습니다.
기본적으로 행렬 곱셈 수학을 알고 있다면 이해가 빠르게 가능할 것 입니다.

dfs를 사용하여 하나씩 계산하기에는 시간초과가 나게 되므로 답을 구할 수 있는 점화식을 찾아야 합니다.
행렬이 A,B,C,D로 4개가 주어진다면
A(B(CD))
A((BC)D)
(AB)(CD)
((AB)C)D
이러한 계산 방법이 나올 것입니다.
이를 DP로 구현하면

DP[a][b] = a번째 행렬부터 b번째 행렬까지의 최소 연산 횟수

가 될 수 있습니다.
이를 점화식으로 만들어내면

DP[a][b] = min(DP[a][b], DP[a][k] + DP[k+1][b] + (matrix[a][0] * matrix[k][1] * matrix[b][1]));

이 만들어진다.
연쇄행렬 최소곱셈 알고리즘을 찾아보고 동작을 시켜본 후 dp맵을 확인해보면 어떤 식으로 동작하는지 좀 더 자세히 알 수 있다.

전체 코드

이번 문제는 문제의 맞는 점화식을 찾아서 풀 수 있는 어려운 문제였습니다.
연쇄행렬 최소곱셈 알고리즘을 좀 더 공부하는 것이 좋을 것 같습니다.

#include<bits/stdc++.h>
#include <string>
#include <vector>

using namespace std;

int answer;
vector<vector<int>> matrix;
int dp[201][201];

int solve(int n)
{
    int a, b;
    for(int i = 0; i < n; i++)
    {
        for(int j = 0; j < n-i; j++)
        {
            a = j;
            b = j+i;
            if(a == b)
            {
                dp[a][b] = 0;
            }
            else
            {
                dp[a][b] = 2100000000;
                for(int k = a; k < b; k++)
                {
                    dp[a][b] = min(dp[a][b], dp[a][k] + dp[k+1][b] + (matrix[a][0] * matrix[k][1] * matrix[b][1]));
                }
            }
        }
    }
    return dp[0][n-1];
}

int solution(vector<vector<int>> matrix_sizes) {
    int answer = 0;
    matrix = matrix_sizes;
    
    answer = solve(matrix_sizes.size());
    
    return answer;
}

점화식 찾기와 알고리즘을 이해하려 적은 그림판을 보니 문제가 어렵긴 했나 보다.

출처

https://school.programmers.co.kr/learn/courses/30/lessons/12942