[Python] 11404: 플로이드

https://www.acmicpc.net/problem/11404
알고리즘 분류 : 최단 경로 > 플로이드-워셜

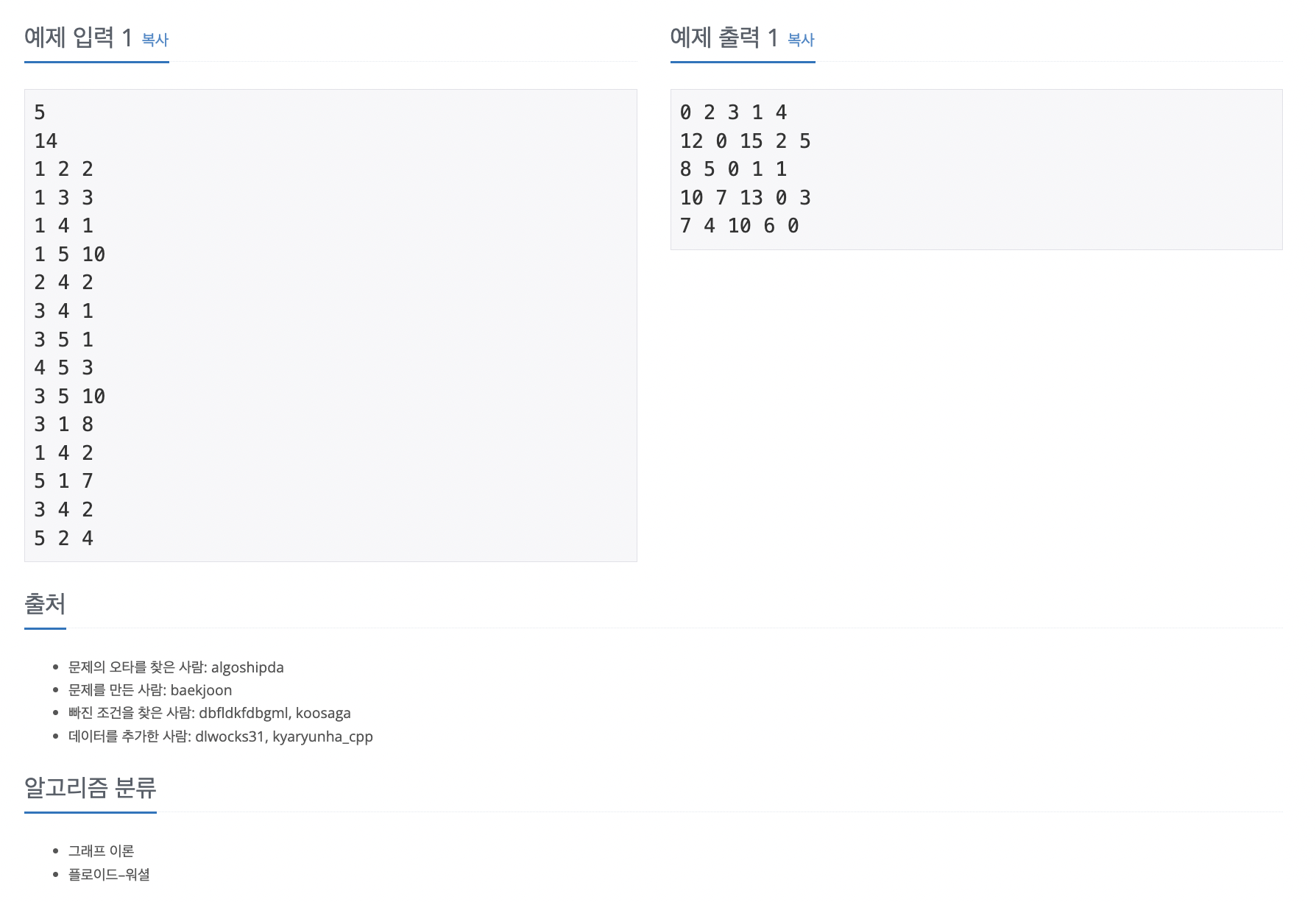
문제:
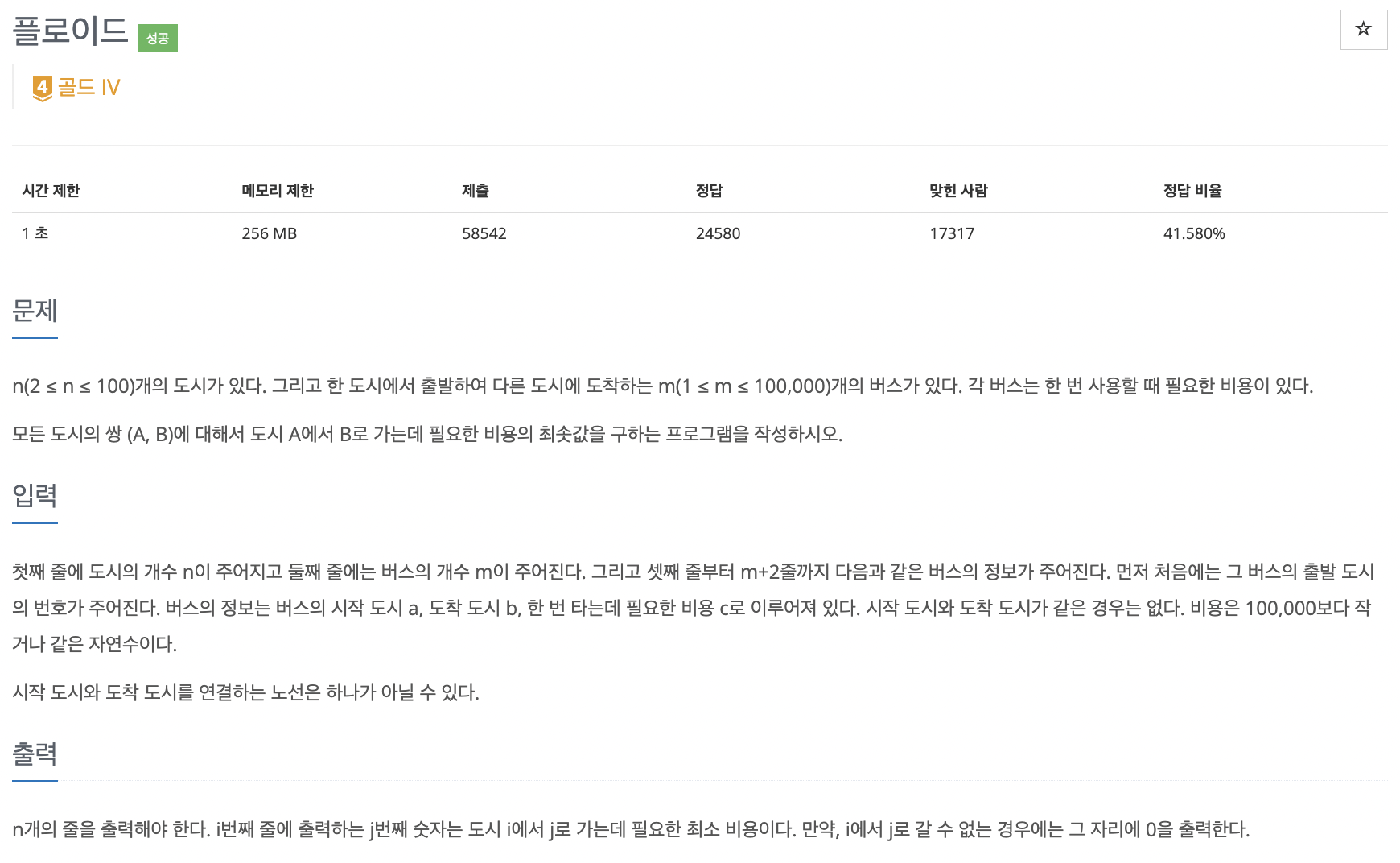
n 개의 도시 (2 ≤ n ≤ 100)
m 개의 버스 (1 ≤ m ≤ 100,000)
각 버스는 한 번 사용할 때 필요한 비용 존재.

모든 도시의 쌍 (A, B)에 대해,
도시 A에서 B로 가는데 필요한 비용의 최솟값을 구하는 프로그램을 작성하라.

입력 :

• 도시의 개수 n
• 버스의 개수 m
• m 개의 버스에 대해 : a (시작 도시), b (도착 도시), c (버스 비용)
  (시작 도시와 도착 도시가 같은 경우는 없고, c ≤ 100,000인 자연수)

출력 :
i번째 줄의 j번째 숫자 -> 도시 i에서 j로 가는데 필요한 최소 비용
i에서 j로 갈 수 없는 경우 -> 0을 출력

풀이:
다른 블로그의 코드를 참고하여 풀었음.

INF = int(1e9) # 무한의 숫자 설정

# 도시(vertex), 버스(edge) 입력받기
N = int(input())
M = int(input())

# 플로이드-워셜은 2차원 배열이 필요하다.
graph = [[INF] * (N+1) for _ in range(N+1)] # 출력할 최소 비용 2차원 배열 설정. 도시는 1번째 도시부터니까 N+1로 설정, 전부 INF로 초기화
for i in range(1, N+1): # 가장 먼저 시작도시와 도착도시가 같은 경우는 0으로 설정
    graph[i][i] = 0
    
for _ in range(M):
    a, b, c = map(int, input().split()) # 버스 정보 입력받을 때마다
    # 더 비용이 적다면 최신화
    graph[a][b] = min(graph[a][b], c)

# graph[a][b]와 a->k->b 로 다른 도시를 통해서 가는 경우를 비교해 더 작은 비용의 값을 넣어줌.
for k in range(1, N+1):
    for a in range(1, N+1):
        for b in range(1, N+1):
            graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])
                
# INF의 값은 마지막에 0으로 바꿔서 출력
for x in range(1, N+1):
    for y in range(1, N+1):
        if graph[x][y] == INF: print(0, end=' ')
        else: print(graph[x][y], end=' ')
    print()