[ Algorithm ] Dynamic Programming

Dynamic Programming, DP

동적 계획법은 이미 했던 연산이 반복되는 결점을 보완하기 위해 고안되었다.
처음 진행하는 연산을 기록해두고,
이미 진행했던 연산이라면 다시 연산하는 것이 아니라 기록되어 있는 값을 가져온다.

Example - Fibonacci Sequence

(0), 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...

피보나치 수열은 보통 재귀를 통해 표현된다.

// recursive by C
int fibo(int n)
{
		if (n <= 2)
			return 1;
		else
			return fibo(n - 1) + fibo(n - 2);
}

// recursive by Swift
func fibo(_ n : Int) -> Int {
    if n <= 2 {
        return 1
    } else {
        return fibo(n - 1) + fibo(n - 2)
    }
}

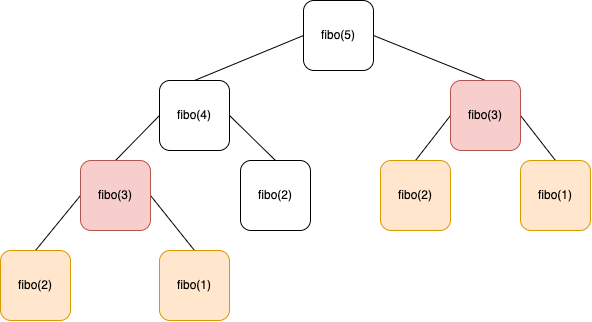
fibo(5) 를 구하기 위해서,
이미 진행된 연산임에도 fibo(3) 연산을 다시 수행해야 하는 것을 볼 수 있다.

// DP [ Dynamic Programming ] by C
int fiboCache[100] = {0, };

int fibo(int n)
{
	if (n <= 2)
		return 1;
	if (fiboCache[n] == 0)
		fiboCache[n] = fibo(n - 1) + fibo(n - 2);
	return fiboCache[n];
}

// DP [ Dynamic Programming ] by Swift
var fiboCache: [Int] = Array(repeating: 0, count: 101)

func fibo(_ n: Int) -> Int {
    if n <= 2 {
        return 1
    }
    if fiboCache[n] == 0 {
        fiboCache[n] = fibo(n - 1) + fibo(n - 2)
    }
    return fiboCache[n]
}

연산한 값들이 저장될 fiboCache 라는 배열을 생성하고,
변수 n 이 2 이하일 경우, 1 을 반환하고
그 이상일 경우에는 fiboCache[n] 에 연산 값이 있는지 검사한다.

저장된 연산 값이 없는 경우에는 새로 연산하여
연산한 값을 저장하고 반환한다.

미리 연산한 값이 존재한다면 바로 fiboCache[n] 을 반환할 수 있을 것이다.

Pros and Cons of DP

동적 계획법은 모든 방법을 일일이 검토하여 최적의 해를 찾아내는 방식의 알고리즘이다.
모든 방법을 검토해 보고 결과적으로 효율적인 값을 택한다.

모든 방법을 검토한다는 점에서 다른 알고리즘보다 시간이 더 걸린다고 말할 수 있지만,
결과적으로는 항상 최적의 해를 구할 수 있다는 이점을 가지고 있다.

---

📚 Reference
[자료구조와 알고리즘] 동적 계획법(Dynamic Programming, DP)