[NLP] 6. Topic Modeling이란?

서쿠·2025년 1월 28일

NLP 강의노트

NLP 강의요약

목록 보기

6/6

1. Topic Modeling이란?

본 강의는 DSBA 강필성 교수님의 강의를 참조하여 작성되었습니다.

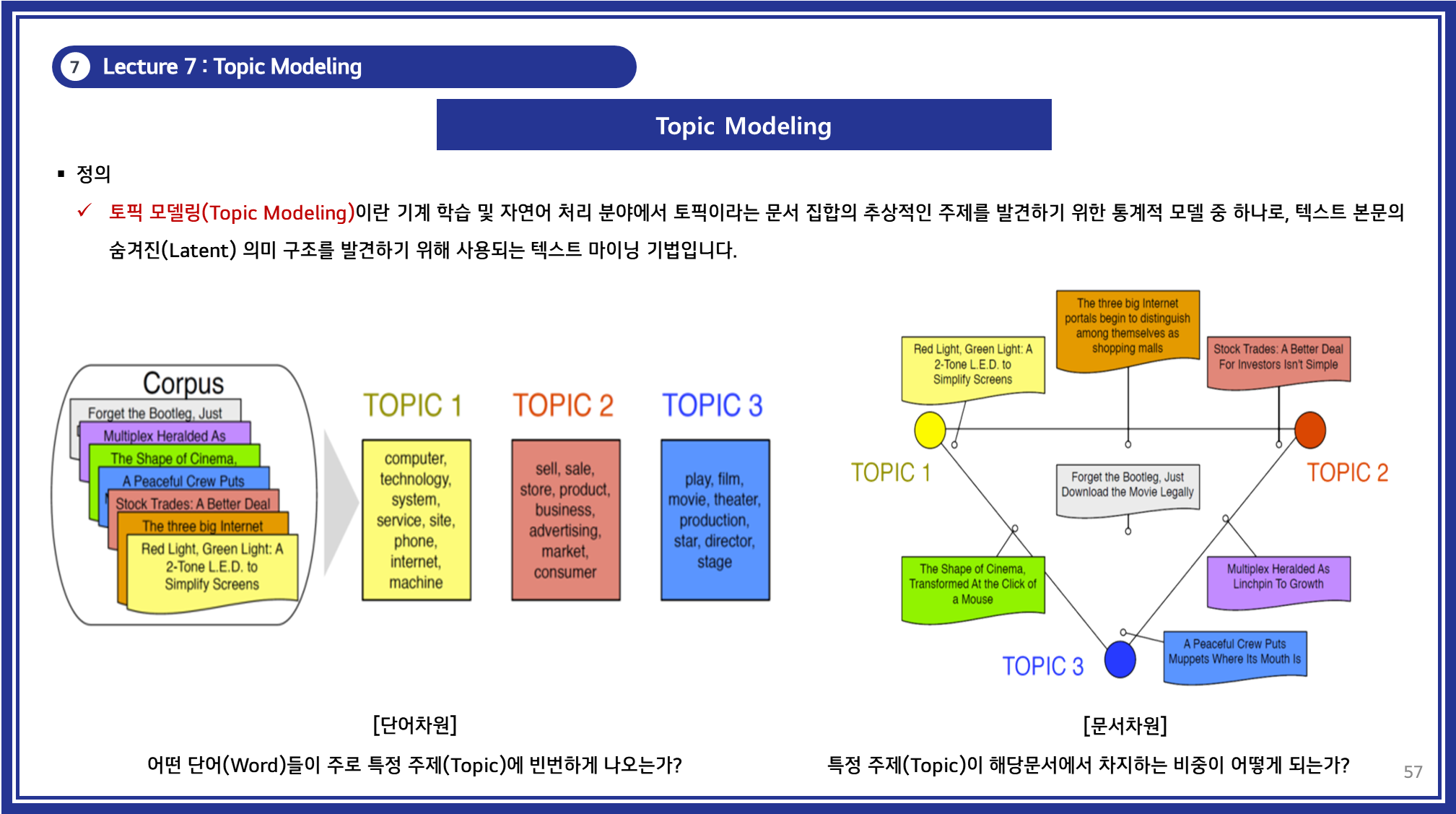
Topic Modeling은 기계 학습 및 자연어 처리 분야에서 문서 집합 내에서 잠재적인 주제(Latent Topic)를 발견하기 위해 사용하는 통계적 모델링 기법입니다.

주어진 문서에서 반복적으로 등장하는 단어 패턴을 분석하여 문서를 특정 주제로 분류하는 역할을 합니다.

Topic Modeling을 활용하면 방대한 문서 데이터에서 잠재적인 의미 구조(Latent Structure)를 자동으로 학습할 수 있습니다.

특히, 비지도 학습(Unsupervised Learning) 기반으로 작동하기 때문에 사전에 레이블링된 데이터 없이도 활용할 수 있습니다.

이러한 특성으로 인해 데이터 레이블이 부족한 상황에서 유용하게 활용될 수 있으며, 문서 분류, 추천 시스템, 정보 검색 등의 다양한 응용 분야에서 중요한 역할을 합니다.

주요 특징

문서 내에서 주요 주제를 추출하는 기법
비지도 학습(Unsupervised Learning)을 기반으로 작동
단어 간의 출현 빈도와 관계를 분석하여 주제 분포(Topic Distribution)를 도출
뉴스 기사, 연구 논문, 고객 리뷰 등의 대량의 문서 데이터에서 주요 주제를 자동으로 분류하는 데 활용됨
문서 내의 단어 출현 패턴을 기반으로 의미적 구조를 찾아내어 숨겨진 관계를 드러낼 수 있음

2. Topic Modeling의 접근법

Topic Modeling을 수행하는 다양한 접근법이 존재합니다.

크게 행렬 분해(Matrix Factorization) 기반 접근과 확률 모델(Probabilistic Model) 기반 접근으로 나눌 수 있습니다.

행렬 분해 기반(Matrix Factorization) 접근
- Singular Value Decomposition (SVD) 기반 차원 축소 기법 활용
- 단어와 문서 간의 관계를 저차원 공간에서 해석
- Example
  - Latent Semantic Analysis (LSA)
  - Non-negative Matrix Factorization (NMF)
확률 모델(Probabilistic Model) 기반 접근
- 문서와 단어가 확률적 토픽 분포를 따르는 확률 모델
- 베이즈 추론을 이용하여 문서의 토픽 분포를 학습
- Example
  - Probabilistic Latent Semantic Analysis (pLSA)
  - Latent Dirichlet Allocation (LDA)

2.1 행렬 분해 기반(Matrix Factorization) 접근

정의:
- 행렬 분해 기반 접근(Matrix Factorization Approach)은 문서-단어 행렬(Term-Document Matrix)을 행렬 분해(Matrix Factorization) 기법을 통해 저차원 잠재 의미 공간(Latent Semantic Space)으로 변환하는 방식입니다.
핵심 개념:
- 고차원 문서-단어 행렬을 저차원 잠재 의미 공간으로 압축 하여 주제를 추출하는 방식
- SVD, NMF 등의 기법을 통해 행렬을 분해하고 이를 통해 주제를 학습
  - SVD: Singular Value Decomposition
  - NMF: Non-negative Matrix Factorization
- 단어와 문서 간의 관계를 벡터 공간 내에서 수치적으로 분석
주요 기법:
1. Latent Semantic Analysis (LSA)
  - Singular Value Decomposition (SVD)을 활용하여 문서-단어 행렬을 분해
  - 단어와 문서를 저차원 벡터 공간에 매핑하여 의미적 유사성을 분석
  - 정규 분포를 가정하며, 확률적 해석이 어렵다는 단점이 있음
2. Non-negative Matrix Factorization (NMF)
  - 문서-단어 행렬을 비음수 행렬(Non-negative Matrix)로 분해하여 의미를 해석
  - 모든 요소가 0 이상이므로 해석이 직관적이며 의미적인 토픽을 추출하는 데 유리

(참고) Singular Value Decomposition (SVD)나 Non-negative Matrix Factorization (NMF)는 차원축소 기법의 일종이라고 봐도 무방합니다. (=> 이는 두 기법 모두 Matrix를 분해하기 때문)

이와 관련하여 좋은 참고 자료가 있어서 공유합니다. 아래 해당 내용에 대해서 다룰 예정임.

링크 : https://www.slideshare.net/madvirus/pca-svd#4

장점:
✔ 연산 속도가 상대적으로 빠르고 구현이 용이함
✔ 노이즈 제거 및 의미적 압축이 가능하여 문서 간 유사성 분석에 적합
✔ 차원 축소를 통해 문서와 단어의 관계를 시각적으로 분석 가능
단점:
✖ 확률 기반 접근이 아니므로 불확실성을 다루기 어려움
✖ 정규 분포를 가정하기 때문에 실제 데이터의 분포를 반영하지 못할 가능성이 있음
✖ 새로운 문서를 추가하면 기존 모델을 다시 학습해야 함

2.2 확률 모델(Probabilistic Model) 기반 접근

정의:
- 확률 모델 기반 접근(Probabilistic Model Approach)은 (1) 문서는 여러 개의 잠재적인 주제(Topic)로 구성되어 있으며, (2) 각 주제는 특정 단어의 확률적 분포를 따른다는 가정하에 문서 내 단어의 주제 분포를 추론하는 방식입니다.
핵심 개념:
- 문서는 여러 개의 주제(Topic)로 구성되며, 각 주제는 특정 단어들의 분포를 가짐
- 주어진 문서에서 단어가 생성될 확률을 기반으로 주제 분포를 추정
- 베이즈 추론(Bayesian Inference)을 활용하여 확률적 토픽 모델링 수행
주요 기법:
1. Probabilistic Latent Semantic Analysis (pLSA)
  - 문서의 단어 출현 확률을 잠재적인 주제(Topic) 분포를 이용하여 설명
    - 확률 모델을 이용해 문서-토픽 분포 $P(z|d)$ 및 토픽-단어 분포 $P(w|z)$ 를 학습
    - EM(Expectation-Maximization) 알고리즘을 활용하여 파라미터를 추정
2. Latent Dirichlet Allocation (LDA)
  - pLSA의 한계를 개선한 베이지안 확률 모델
  - 문서의 토픽 분포( $\theta$ )와 토픽의 단어 분포( $\phi$ )를 Dirichlet 분포에서 샘플링
  - Gibbs Sampling 또는 변분 추론(Variational Inference)을 사용하여 확률을 추정
장점:
✔ 문서 내에서 각 주제의 확률적 분포를 학습할 수 있음
✔ 새로운 문서가 추가되어도 기존 모델을 재학습할 필요 없이 사전 학습된 주제 분포를 활용 가능
✔ 베이지안 접근을 활용하면 데이터의 불확실성을 보다 잘 반영할 수 있음
단점:
✖ 학습 과정이 상대적으로 복잡하고 계산 비용이 높음
✖ Gibbs Sampling 또는 Variational Inference를 사용해야 하므로 대규모 데이터에서는 학습 시간이 길어질 수 있음
✖ 주제 수(K)를 사전에 정해야 하며, 이를 잘못 설정하면 모델 성능이 저하될 수 있음

📌 행렬 분해 접근 vs 확률 모델 접근 비교 정리

구분	행렬 분해 (Matrix Factorization)	확률 모델 (Probabilistic Model)
핵심 아이디어	문서-단어 행렬을 저차원으로 압축	문서는 여러 개의 주제로 구성되며 각 주제는 특정 단어의 확률적 분포를 가짐
주요 기법	LSA (SVD), NMF	pLSA, LDA
결과 해석 방식	선형 대수 기반	확률 기반
확률적 해석 가능 여부	❌ (확률 모델이 아님)	✅ (확률적 모델)
새로운 문서 처리	기존 모델을 다시 학습해야 함	기존 모델을 활용 가능
계산 비용	상대적으로 낮음	상대적으로 높음
적용 사례	검색 엔진, 추천 시스템, 문서 유사도 분석	문서 분류, 토픽 탐색, 트렌드 분석
단점	확률적 해석이 어려움	계산 비용이 높고 학습이 복잡함

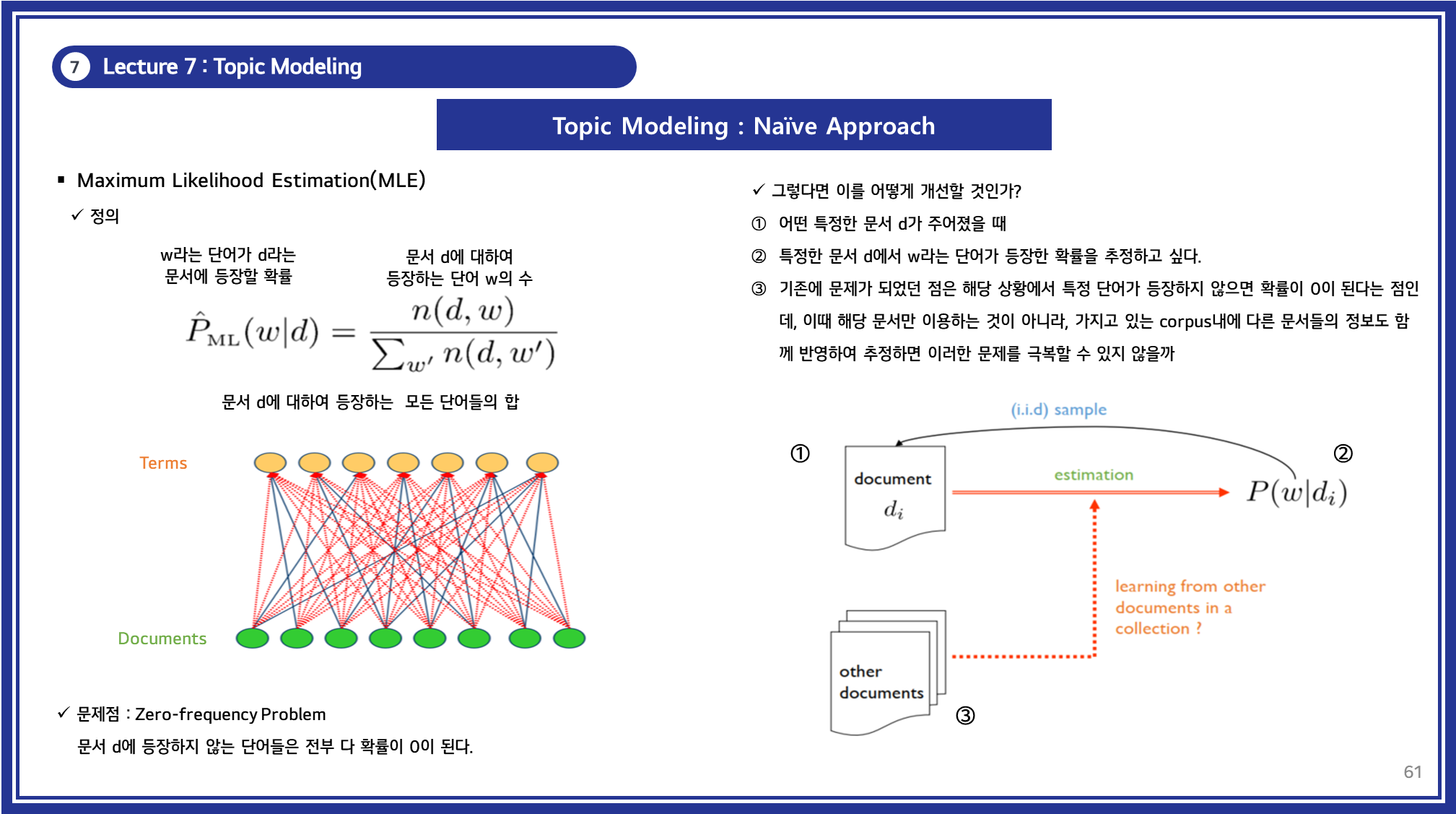
(참고) Naïve Approach (MLE, Maximum Likelihood Estimation)

특정 문서 (Document, d)에서 단어 (Word, w)가 등장할 확률을 MLE(최대 우도 추정)로 구하는 방법.

MLE는 확률 모델 기반 접근법 중 가장 단순한 방식으로 볼 수 있습니다.
- 하지만, LDA나 pLSA와 달리 잠재 변수(Latent Variable) 개념이 없으며, 단순히 문서별 단어 출현 빈도를 기반으로 확률을 계산하기 때문에 일반적인 Topic Modeling과는 차이가 있습니다.
아이디어:
- 문서 내 단어의 단순 빈도수를 기반으로 해당 단어가 특정 문서에서 발생할 확률을 직접 계산

한계점:
- MLE는 단순한 빈도 기반 확률 추정 방법으로 직관적이지만, 일반화 성능이 부족할 수 있습니다.
- 문서 내에 없는 단어는 확률이 0으로 설정되며, 데이터의 희소성 문제를 해결하기 어렵습니다.
보완 방법:
- Zero-Frequency Problem (빈도 0 문제)가 발생하는 경우, 이를 보완하기 위해 스무딩(Smoothing) 기법이 필요합니다.

❓ Zero-Frequency Problem (빈도 0 문제)이란?
Zero-Frequency Problem은 학습 데이터에 없는 단어나 단어 조합이 등장했을 때 확률이 0이 되어 모델이 일반화되지 못하는 문제입니다.

이를 해결하기 위해 다양한 스무딩(Smoothing) 기법이 사용되며, 데이터의 희소성 정도에 따라 적절한 방법을 선택해야 합니다.

간단한 문제 해결에는 Add-k 스무딩(Laplace)이 적절합니다.

데이터 희소성이 높은 경우에는 Good-Turing 스무딩이 효과적입니다.

실제 언어 모델에서 가장 성능이 좋은 방법은 Kneser-Ney 스무딩입니다.

따라서, 스무딩 기법을 적용하면 희소한 데이터에서도 언어 모델이 보다 일반화된 확률을 추정할 수 있으며, 검색, 번역, 텍스트 생성 등 다양한 NLP 작업에서 성능을 향상시킬 수 있습니다.

스무딩 기법	특징	장점	단점
Additive Smoothing (Add-k)	모든 빈도에 작은 값을 추가	구현이 간단	과도하게 균등한 확률 분포
Good-Turing Smoothing	빈도 0인 단어를 낮은 빈도를 기반으로 추정	희소한 데이터에 적합	높은 빈도의 단어에 적용이 어려움
Kneser-Ney Smoothing	문맥 내 사용 빈도를 고려	가장 효과적이고 정확도 높음	구현이 복잡

위에서 Topic Modeling을 분류해봤으니 이제 각각의 컨셉에 대해서 자세하게 살펴보도록 하겠습니다.

3. Latent Semantic Analysis (LSA)

3.1. Latent Structure (잠재 구조)

3.1.1 개념

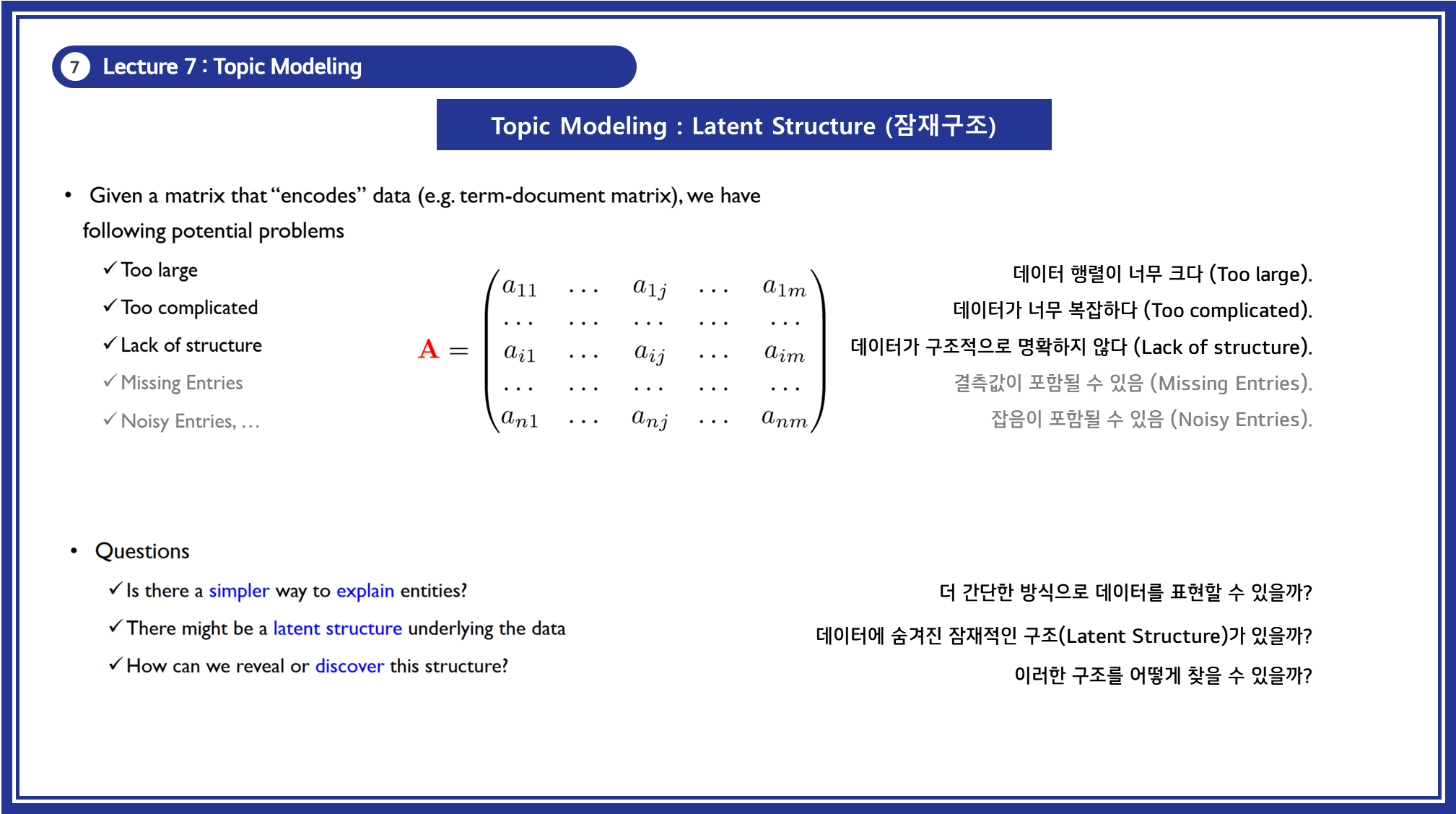
데이터를 행렬로 표현하면, 행렬의 크기가 너무 크거나, 너무 복잡하여 분석이 어렵거나, 명확한 구조가 드러나지 않는 문제가 발생할 수 있음.
- 이러한 데이터를 더 쉽게 해석할 수 있는 방법이 필요함.
Latent Structure(잠재 구조)는 데이터 속에 숨겨진 패턴이나 구조를 찾아내는 과정을 의미함.
- 이를 통해, 보다 단순하고 의미 있는 표현을 얻을 수 있음.

3.1.2 문제점

데이터 행렬이 너무 크다 (Too large).
데이터가 너무 복잡하다 (Too complicated).
데이터가 구조적으로 명확하지 않다 (Lack of structure).
결측값이나 잡음이 포함될 수 있음 (Missing Entries, Noisy Entries).

3.1.3 해결책: Latent Structure 찾기

더 간단한 방식으로 데이터를 표현할 수 있을까?
데이터에 숨겨진 잠재적인 구조(Latent Structure)가 있을까?
이러한 구조를 어떻게 찾을 수 있을까?

3.2. Matrix Decomposition (행렬 분해)

3.2.1 개념

데이터 행렬을 단순화하여, 원래 데이터의 중요한 구조만을 유지하는 작은 행렬로 분해하는 과정.
행렬 분해를 수행하면 원본 데이터보다 더 작은 차원의 표현을 만들 수 있으며, 의미 있는 패턴을 찾아낼 수 있음.

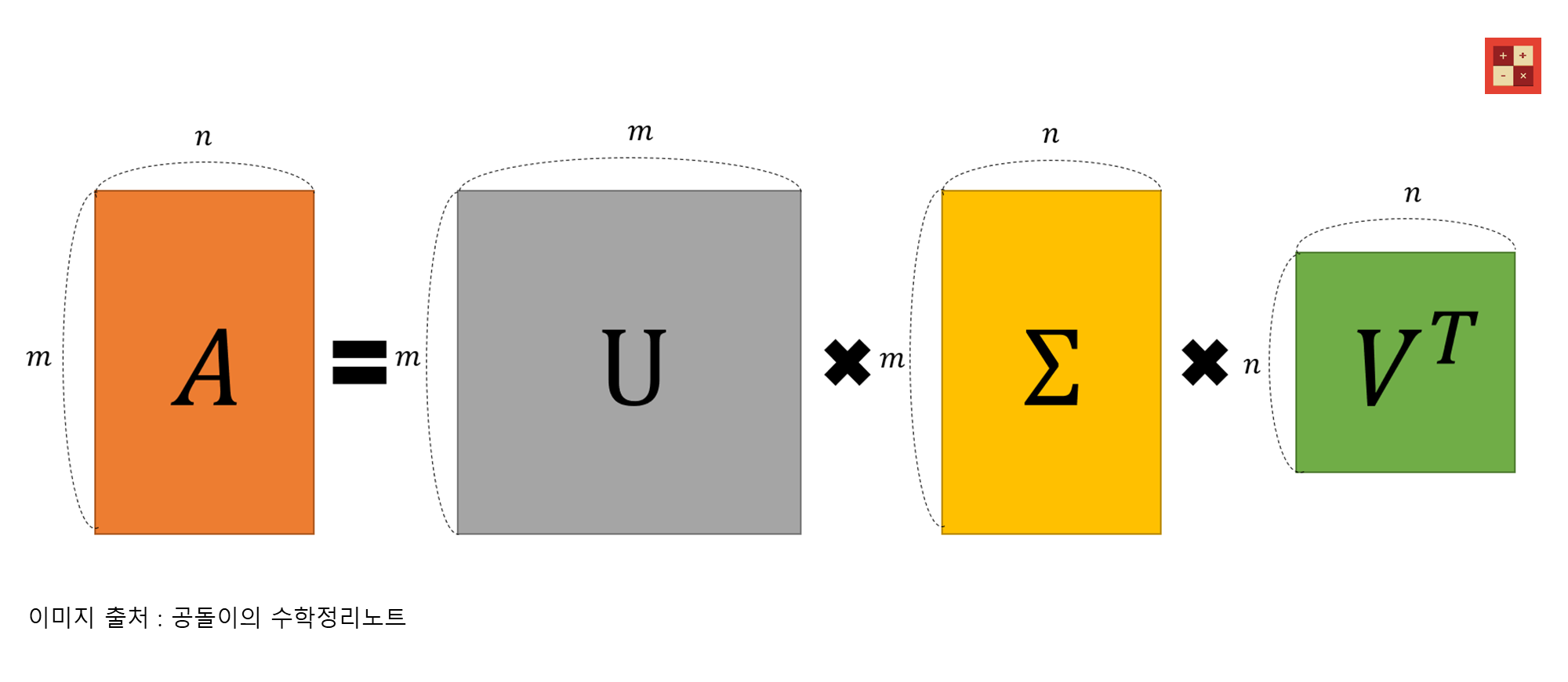
3.2.2 수학적 표현

A \approx \hat{A} = L \cdot R

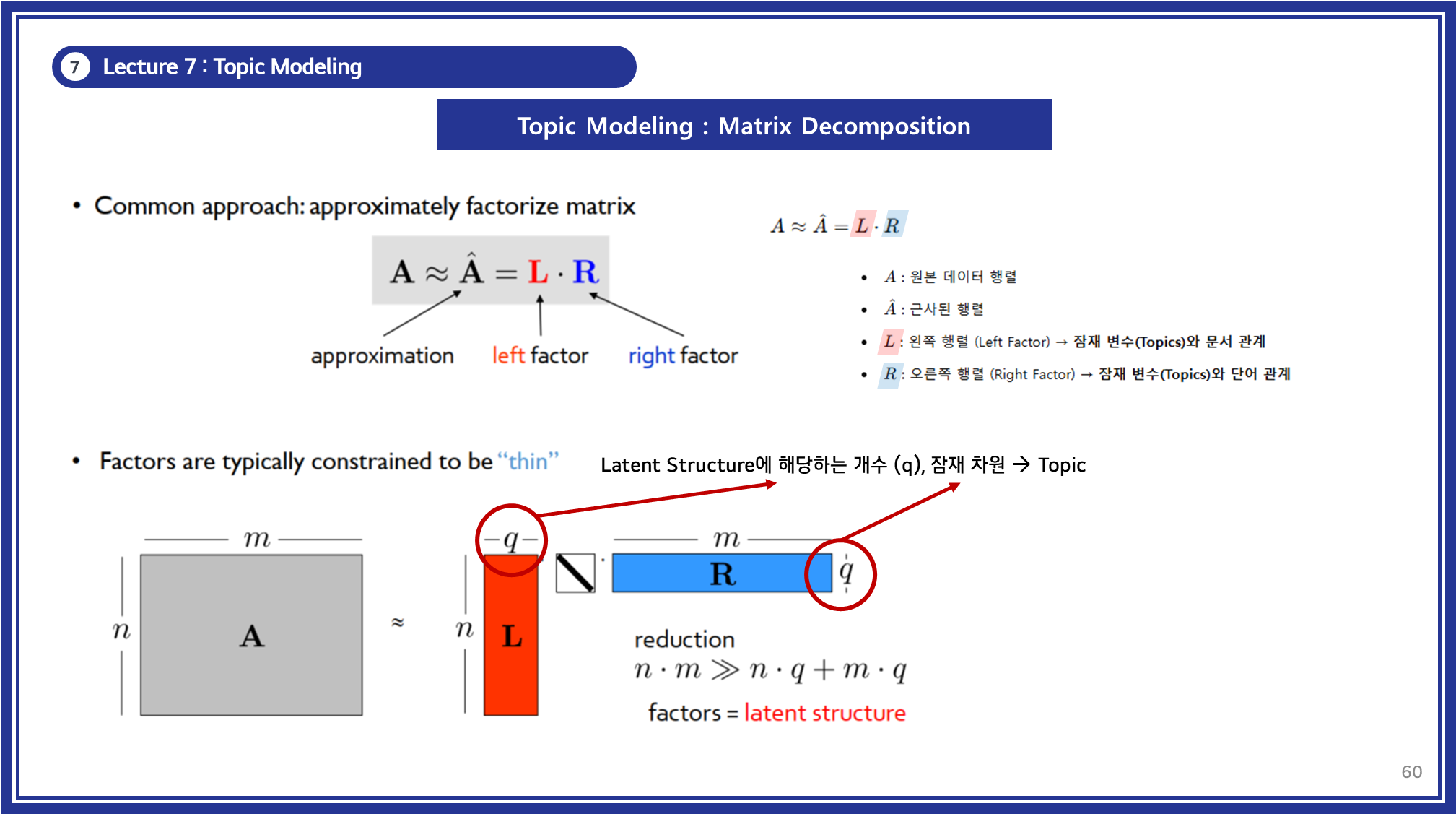
$A$ : 원본 데이터 행렬
$\hat{A}$ : 근사된 행렬
$L$ : 왼쪽 행렬 (Left Factor, $n · q$ ) → 잠재 변수(Topics)와 문서 관계
$R$ : 오른쪽 행렬 (Right Factor, $m · q$ ) → 잠재 변수(Topics)와 단어 관계
$q$ : 잠재 차원(Latent Dimension) → 주제(Topics)의 개수

3.2.3 특징

데이터 크기를 줄임 → 계산량을 감소시킴.
잠재 의미 구조(Latent Structure)를 추출 → 패턴을 분석하는 데 유용.
각 요소들이 잠재 주제를 반영 → 의미 있는 데이터 표현 가능.

3.3. LSA (Latent Semantic Analysis)

3.3.1 개념

LSA는 행렬 분해를 이용하여 문서와 단어 간의 관계를 잠재 의미 공간에서 분석하는 방법입니다.
- Topic modeling 시에 LSA는, Singular Value Decomposition (SVD, 특이값 분해)을 사용하여 문서-단어 행렬을 저차원 공간으로 변환함.

❓ Singular Value Decomposition (SVD, 특이값 분해)란?

Singular Value Decomposition (SVD, 특이값 분해)는 행렬을 세 개의 직교 행렬의 곱으로 분해하는 선형 대수 기법입니다.

이를 통해 고차원의 행렬을 저차원 잠재 의미 공간으로 변환할 수 있으며, 차원 축소, 노이즈 제거, 데이터 압축 등에 널리 사용됩니다.

SVD의 핵심 원리

행렬을 더 작은 의미 있는 구성 요소로 분해하여 주요한 패턴을 추출

데이터 차원을 줄이는 동시에 중요한 정보만 유지 가능

특이값(Singular Value)을 사용하여 행렬의 가장 중요한 구조를 학습

💌 SVD 수식 정리
SVD를 통해 입력 행렬 $A$ 는 세 개의 행렬로 분해되는데, 각 행렬은 서로 다른 역할을 합니다.
$A = U \Sigma V^T$

💬 기호 설명

$A$ (입력 행렬, $m \times n$ )
- 데이터를 포함한 원본 행렬 (Original Matrix)
- 이 행렬은 행(row)과 열(column) 간의 관계를 나타내는 구조를 가짐
$U$ (왼쪽 직교 행렬, $m \times m$ )
- A의 열(column) 방향으로 주어진 데이터의 주성분(Principal Component)을 나타냄
  - 즉, $U$ 의 열 벡터들은 A의 열 벡터들을 새로운 직교 기저(orthonormal basis)로 표현하는 역할
- 각 행(row)은 원래의 $A$ 의 행을 새로운 기저에서 표현한 것
- 각 열(column)은 A의 주요한 특징(feature)을 나타내는 벡터 (A행렬의 열의 주성분)
  - 예: 고유 얼굴(Face Recognition) 분석에서 특정 얼굴 특징을 나타내는 벡터
$\Sigma$ (대각 행렬, $m \times n$ )
- A에서 중요한 정보(특이값, Singular Value)를 포함하는 행렬
- 대각 원소만 존재하며, 대각선의 값(특이값)은 A의 주요한 패턴(Principal Components)의 강도를 나타냄
- 큰 특이값(Singular Value)일수록 데이터에서 중요한 정보
- 작은 특이값은 노이즈나 덜 중요한 정보를 의미
  - 예: 압축(compression) task에서 작은 특이값을 제거하면 중요한 정보만 유지됨
$V^T$ (오른쪽 직교 행렬, $n \times n$ )
- A의 행(row) 방향으로 주어진 데이터의 주성분을 나타냄
  - 즉, $V^T$ 의 행 벡터들은 A의 행 벡터들을 새로운 직교 기저에서 표현
- 각 열(column)은 원래의 $A$ 의 열을 새로운 기저에서 표현한 것
- 각 행(row)은 A의 주요한 특징(feature)을 나타내는 벡터 (A행렬의 행의 주성분)
  - 예: 문서 분석에서 주제(Topic)를 나타내는 벡터

(참고) 👀 SVD 기하학적 해석
📌 SVD는 본질적으로 A라는 선형 변환을 "회전(Rotation) → 크기 조정(Scaling) → 다시 회전(Rotation)"하는 과정으로 해석할 수 있습니다.
$A = U \Sigma V^T$

1️⃣ $V^T$ : 기저 변환 (Basis Change)

데이터(행렬 A)를 적절한 직교 좌표계(Orthogonal Basis)로 변환

즉, 원래 좌표계에서 새로운 좌표계로 변환하는 역할

2️⃣ $\Sigma$ : 축 방향 스케일링 (Scaling along Principal Axes)

각 좌표축 방향으로 데이터를 변형(크기 조절)

즉, 중요한 축(Principal Component) 방향으로 데이터를 늘리고 줄이는 역할

3️⃣ $U$ : 다시 회전 (Final Rotation back to original space)

변형된 데이터를 원래 좌표계로 회전 변환

💡 즉, SVD는 데이터를 보다 잘 정렬된 (직교) 좌표계로 변환하고, 그 안에서 주축을 따라 크기 조절한 후, 다시 원래 공간으로 변환하는 과정으로 볼 수 있습니다.

살짝 개념적인 이야기를 하다가 옆으로 빠졌는데 다시 LSA에 대해서 살펴보도록 하겠습니다.

LSA는 문서-단어 행렬(document-term matrix)에 SVD를 적용하여 숨겨진 의미(latent semantics)를 추출하는 기법입니다.
LSA를 통해 아래와 같은 것들을 수행할 수 있습니다:
- 텍스트 데이터를 수치화하고, 문서-단어 행렬로 표현
- SVD를 적용하여 중요한 의미만 남기고, 노이즈 제거
- 차원 축소를 통해 문서 간 의미적 유사도를 파악

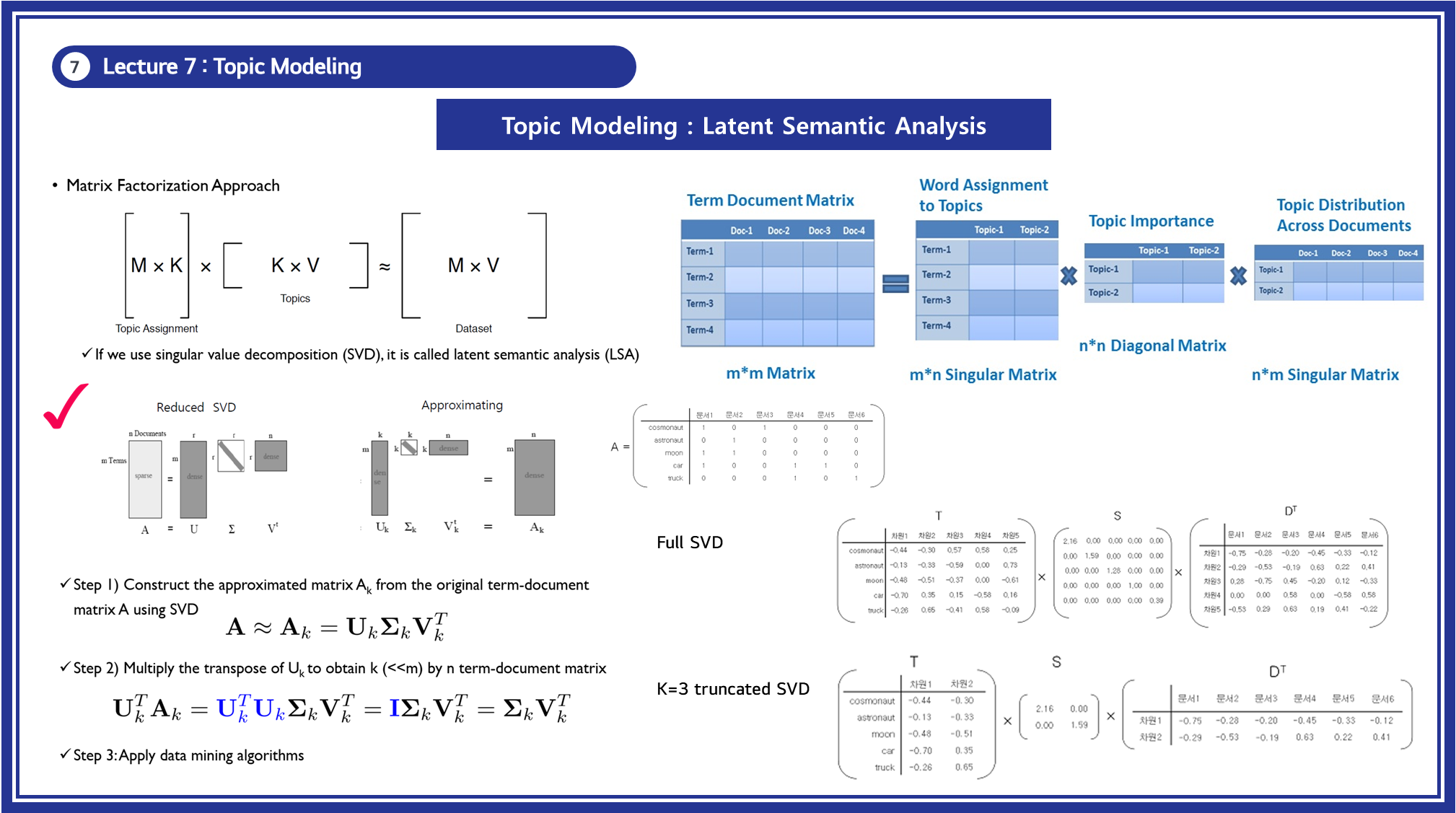
3.3.2 LSA의 수학적 표현

행렬분해 기법(SVD)인 LSA를 수식으로 표현하면 아래와 같이 나타낼 수 있습니다:

A \approx U_k \Sigma_k V_k^T

$A$ (Term-Document Matrix): 단어-문서 행렬 (입력 데이터)
$U_k$ (Left Singular Vectors): 단어와 주제(Topic) 간의 관계
$\Sigma_k$ (Singular Values, 특이값 행렬): 주제의 중요도를 나타냄
$V_k^T$ (Right Singular Vectors): 문서와 주제(Topic) 간의 관계

3.3.3 LSA의 주요 과정

Step 1: 원본 행렬 $A$ 를 SVD로 분해

A \approx U_k \Sigma_k V_k^T

여기서 $k$ 는 선택한 잠재 차원의 수
- 보통 $k$ 를 기존 차원보다 작게 설정하여 의미 있는 정보만 유지.
$U_k, \Sigma_k, V_k^T$ 를 사용하여 원래 행렬을 근사함.

Step 2: 주어진 행렬 $A_k$ 를 이용하여 데이터 분석

U_k^T A_k = U_k^T U_k \Sigma_k V_k^T = \mathbf{I} \Sigma_k V_k^T = \Sigma_k V_k^T

이 과정에서 데이터의 중요한 의미(잠재 의미)를 보존하면서 차원을 축소함.

Step 3: 데이터 분석에 활용

LSA를 통해 도출된 각각의 행렬을 활용하여 데이터 분석을 수행할 수 있습니다.

LSA에서 분해된 행렬 ( $U_k$ , $\Sigma_k$ , $V_k^T$ )은 다양한 방식으로 활용될 수 있으며, 대표적인 응용 사례는 다음과 같습니다.

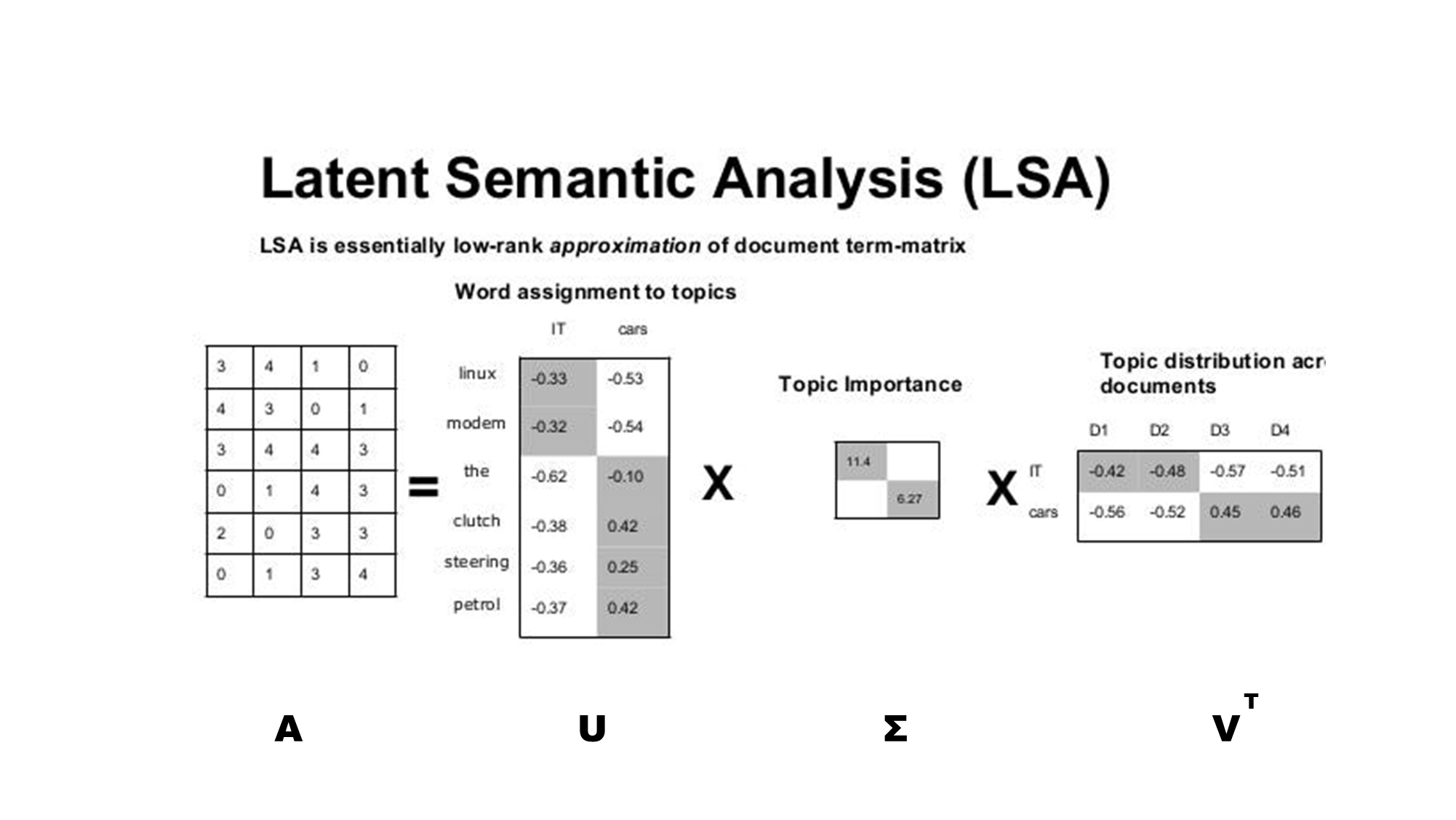
Image Source : https://medium.com/analytics-vidhya/what-is-topic-modeling-161a76143cae

1️⃣ $U_k$ : "토픽별 주요 단어 찾기"

📌 목적: 각 토픽(잠재 의미)을 대표하는 단어를 추출하여 주제를 해석하기 위함.

🤔 설명: $U_k$ 는 단어와 토픽 간의 관계를 나타내는 행렬로, 특정 주제를 구성하는 중요한 단어들을 파악할 수 있습니다.

이를 활용하면 토픽 모델링을 통해 각 주제를 대표하는 단어를 추출할 수 있습니다.

📊 활용 예시:

뉴스 기사에서 주제별 핵심 키워드 추출
논문, 리뷰 데이터에서 주요 토픽을 분석

2️⃣ $V_k$ : "문서 간 유사도 계산"

📌 목적: 문서 간의 의미적 유사도를 계산하여 비슷한 문서를 찾기 위함.

🤔 설명: $V_k$ 는 문서와 토픽 간의 관계를 나타내는 행렬입니다.

이를 활용하면 문서 간의 의미적 유사도를 계산하여 비슷한 문서를 찾을 수 있습니다.

📊 활용 예시:

뉴스 기사 중 비슷한 내용을 다룬 문서 추천
논문 데이터베이스에서 유사한 연구 논문 추천
고객 리뷰에서 비슷한 의견을 가진 리뷰 군집화

3️⃣ $V_k$ : "의미 기반 검색 (Query Expansion)"

📌 목적: 단순 키워드 매칭이 아닌, 의미적으로 연관된 문서를 찾기 위함.

🤔 설명: $V_k$ 를 활용하면 단순 키워드 매칭이 아닌, 의미적으로 관련 있는 문서를 검색할 수 있습니다.

이는 전통적인 검색 엔진과 달리 의미적 유사성을 기반으로 검색 결과를 확장하는 역할을 합니다.

📊 활용 예시:

사용자가 "AI 주식 시장"을 검색하면 "엔비디아 주가 하락", "반도체 주식 변동" 같은 문서 추천
고객이 "배송 늦음"을 검색하면 "배송 지연 보상 정책" 문서 추천
논문 데이터베이스에서 "강화 학습"을 검색하면 "딥러닝 기반 강화 학습" 논문도 추천

3.4 LSA의 특징

✅ 장점:

차원 축소를 통해 잡음을 제거하고 중요한 의미 구조만 유지할 수 있음.
단어 간 의미적 유사성을 찾을 수 있음 (예: Synonym, 의미적으로 가까운 단어들을 유사하게 분석).
검색, 추천 시스템, 문서 분류 등에 활용 가능.

❌ 한계:

확률적 모델이 아니므로, 결과 해석이 어려움 (확률 기반 모델인 LDA와 비교됨).
새로운 문서에 대한 일반화가 어려움 → 기존 학습 데이터가 변하면 다시 학습해야 함.
모든 데이터가 정규 분포를 따른다고 가정함 → 실제 자연어 데이터의 분포와 다를 수 있음.

3.5 LSA의 실습

다음은 LSA 코드 실습입니다.

실제 최신 뉴스 기사를 가져와서 이를 바탕으로 LSA를 수행해보았습니다.
- 기사 제목 : 딥시크가 뭐길래 엔비디아가 대폭락해?…중국 AI 돌풍 (한겨레)
- 링크 : https://www.hani.co.kr/arti/international/international_general/1179929.html

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.decomposition import TruncatedSVD
from sklearn.feature_extraction.text import TfidfVectorizer

# 1. 뉴스 기사 데이터 준비 (예제 문서)

documents = [
    "중국의 저비용 인공지능(AI) 딥시크(DeepSeek)의 등장에 엔비디아 등 미국의 인공지능(AI) 관련 빅테크 기업들이 흔들리고 있다.",
    "딥시크 등장에 기존 인공지능 기업들의 경쟁력이 의심받으며 최악의 주가 폭락이 일어났다.",
    "중국이 값싸고 뛰어난 성능의 인공지능을 개발함으로써, 이 분야에서 미국을 앞설 수 있다는 분석도 나온다.",
    "27일 미국 증시에서는 챗지피티(ChatGPT) 등 생성형 인공지능 출시 이후 증시에서 최대 빅테크 기업으로 성장한 엔비디아가 무려 17% 폭락해, 5890억달러가 증발됐다.",
    "엔비디아 등 미 증시에서 비중이 큰 빅테크 기업들이 일제히 폭락하며 나스닥 지수는 3.1%, 엔스앤피(S&P)500 지수는 1.5%나 떨어졌다.",
    "하지만, 빅테크 기업이 편입되지 않은 다우존스 지수는 0.7% 올랐다.",
    "특히, 인공지능 및 반도체 관련주로 구성된 필라델피아 반도체지수는 9.15%나 폭락해, 지난해 9월3일 7.75% 이후 최대로 떨어졌다.",
    "이 지수가 9% 이상 폭락하기는 코로나19 충격이 가해졌던 지난 2020년 3월18일 이후 처음이다."
]

# 2. TF-IDF 벡터화
vectorizer = TfidfVectorizer()
X = vectorizer.fit_transform(documents)

# 3. LSA 적용 (SVD를 사용하여 차원 축소)
num_topics = 2  # 2개의 주요 주제 추출
svd = TruncatedSVD(n_components=num_topics)
X_lsa = svd.fit_transform(X)

# 4. 단어-토픽 행렬 (U_k)
terms = vectorizer.get_feature_names_out()
word_topic_matrix = pd.DataFrame(svd.components_.T, index=terms, columns=[f"Topic {i+1}" for i in range(num_topics)])

# 5. 문서-토픽 행렬 (V_k)
document_topic_matrix = pd.DataFrame(X_lsa, index=[f"Doc {i+1}" for i in range(len(documents))], columns=[f"Topic {i+1}" for i in range(num_topics)])

# 6. 주요 토픽 별 상위 단어 확인 (가장 중요한 단어 10개 출력)
print("📌 LSA 토픽 별 주요 단어")
for i in range(num_topics):
    print(f"\n🔹 Topic {i+1}")
    print(word_topic_matrix[f"Topic {i+1}"].abs().sort_values(ascending=False).head(10))

# 7. 문서-토픽 분포 시각화
plt.figure(figsize=(10, 6))
sns.heatmap(document_topic_matrix, annot=True, cmap="coolwarm", fmt=".2f")
plt.title("문서별 토픽 분포 (LSA 기반)")
plt.xlabel("토픽")
plt.ylabel("문서")
plt.show()

# 8. 결과 출력
print("\n📌 LSA 단어-토픽 행렬 (U_k)")
print(word_topic_matrix)

print("\n📌 LSA 문서-토픽 행렬 (V_k)")
print(document_topic_matrix)

코드 설명
1. TF-IDF 벡터화를 통해 문서를 수치화된 벡터로 변환 (A 생성)
2. SVD를 사용하여 차원 축소 (𝑘=2)
3. 코사인 유사도(Cosine Similarity) 를 계산하여 문서 간 유사도 측정
4. 유사도 행렬을 출력하여 문서 간의 관계를 확인

분석 수행

(1) $U_k$ , $\Sigma_k$ , $V_k$ 분해 결과

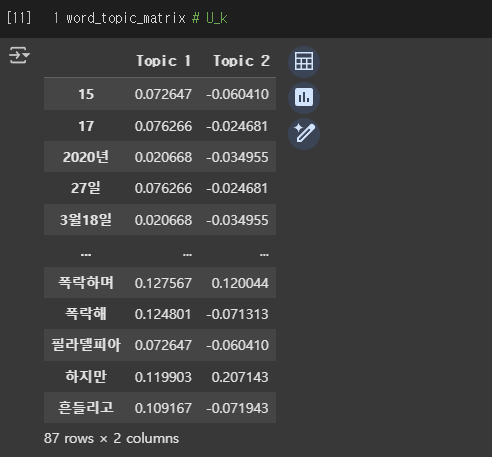
위 코드를 돌리면 각각 다음과 같이 $U_k$ , $\Sigma_k$ , $V_k$ 가 도출되어 나오는 것을 확인할 수 있습니다.
- 단어-토픽 행렬 ( $U_k$ )
- Topic Importance (𝚺)
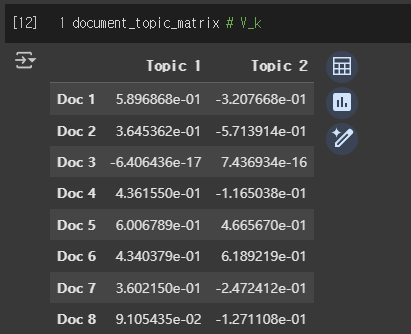
- 문서-토픽 행렬 ( $V_k$ )

(2) Topic 분해 결과 - truncated svd (k=2)

LSA를 통해 뉴스 기사에서 2개의 주요 토픽을 추출했습니다.
- Topic 1: "AI & 증시 폭락 관련"
  => "AI 기업 및 증시 폭락 관련 뉴스"로 해석 가능
- Topic 2: "증시 및 다우존스 상승/하락 관련"
  => "증시 변화와 다우존스 관련 뉴스"로 해석 가능

📌 LSA 토픽 별 주요 단어

🔹 Topic 1
지수는     0.314311
인공지능    0.287213
빅테크     0.274496
ai      0.218333
기업들이    0.198402
엔비디아    0.198402
증시에서    0.170829
떨어졌다    0.167795
등장에     0.163324
딥시크     0.163324
Name: Topic 1, dtype: float64

🔹 Topic 2
지수는     0.374815
인공지능    0.248398
올랐다     0.207143
하지만     0.207143
않은      0.207143
다우존스    0.207143
기업이     0.207143
편입되지    0.207143
딥시크     0.196706
등장에     0.196706
Name: Topic 2, dtype: float64

(3) 문서(문장) 별 토픽 분포

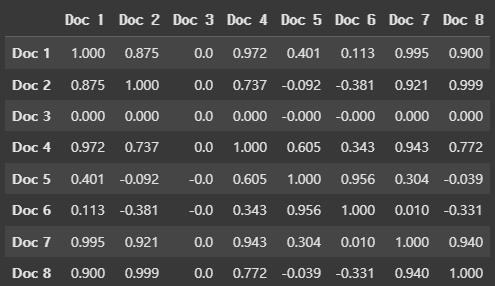
다음은 뉴스 기사의 각 문장들이 각각 어떤 topic에 연관성을 띄는지 분석한 그림입니다.

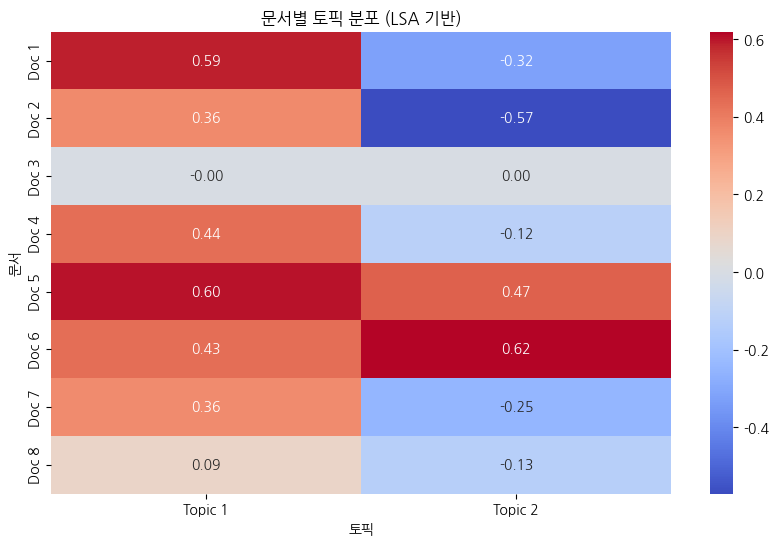
아래와 같이 해석해볼 수 있습니다:

Doc 1, 5 → Topic 1과 강한 연관성 (AI & 증시 폭락 관련 뉴스)
Doc 5, 6 → Topic 2와 강한 연관성 (증시 & 다우존스 관련 뉴스)
Doc 3은 거의 두 개의 토픽과 연관이 없음 (일반적인 내용이거나 LSA에서 의미적 관계가 낮은 문서)
Doc 2, 7 → Topic 1과 밀접한 관계, 하지만 Topic 2와는 반대 성향 (즉, AI 중심 뉴스일 가능성 높음)

🎓 (심화) 추가 분석 시나리오

위에서 정의해보았던 "Step 3: 데이터 분석에 활용"에 대해서 좀 더 심화있게 분석하고 싶다면 아래와 같이 분석을 해보실 수 있습니다.

1️⃣ $U_k$ : 토픽별 주요 단어 찾기

top_n_words = 5
lsa_topic_words = {}
for i in range(num_topics):
    lsa_topic_words[f"Topic {i+1}"] = word_topic_matrix[f"Topic {i+1}"].abs().sort_values(ascending=False).head(top_n_words)
lsa_topic_words_df = pd.DataFrame(lsa_topic_words)
lsa_topic_words_df

2️⃣ $V_k$ : 문서 간 유사도 계산

from sklearn.metrics.pairwise import cosine_similarity
doc_similarity = cosine_similarity(document_topic_matrix)
doc_similarity_df = pd.DataFrame(doc_similarity, index=[f"Doc {i+1}" for i in range(len(documents))], columns=[f"Doc {i+1}" for i in range(len(documents))])
doc_similarity_df

3️⃣ $V_k$ : 의미 기반 검색

query = ["AI 주식 시장"]
query_vector = vectorizer.transform(query)  # TF-IDF 변환
query_lsa = svd.transform(query_vector)  # LSA 변환
query_similarity = cosine_similarity(query_lsa, X_lsa)
top_n = 3
most_relevant_docs = query_similarity.argsort()[0][-top_n:][::-1]
for _doc in most_relevant_docs:
    print(documents[_doc])

4. Probabilistic Latent Semantic Analysis (pLSA)

4.1 pLSA의 등장 배경

Latent Semantic Analysis(LSA)는 Singular Value Decomposition(SVD)을 사용하여 문서와 단어 간의 관계를 저차원 벡터 공간으로 표현하는 방법입니다.

하지만 LSA는 다음과 같은 한계를 가지고 있었습니다.

선형 모델의 한계
- LSA는 행렬 분해 기반의 선형 모델로, 단어와 문서의 관계를 단순한 벡터 공간에서 표현합니다.
  - 하지만 언어 데이터는 종종 비선형적인 관계를 가지며, 단순한 행렬 연산만으로는 의미적 구조를 효과적으로 학습하기 어렵습니다.
확률적 해석의 난해함
- LSA의 결과는 벡터 값으로 나타나며, 이를 확률적인 의미로 해석하기 어렵습니다.
  - 예를 들어, 특정 문서가 특정 토픽을 포함할 확률이나 특정 단어가 특정 토픽에서 발생할 확률 등을 추론하는 것이 어렵습니다.
새로운 문서 일반화 불가능
- LSA는 고정된 문서-단어 행렬을 기반으로 학습하기 때문에, 학습되지 않은 새로운 문서가 등장하면 기존 모델을 확장하는 것이 어렵습니다.
  - 새로운 문서를 처리하려면 기존 행렬을 다시 구성하고 다시 SVD를 수행해야 합니다.
메모리 및 계산량 문제
- SVD 연산은 O(n³)의 복잡도를 가지며, 문서 수가 많아질수록 계산량이 급격히 증가합니다.
  - 따라서 대규모 데이터셋에서 LSA를 적용하는 것은 현실적으로 어려운 경우가 많습니다.

위와 같은 LSA의 한계를 해결하기 위해 Probabilistic Latent Semantic Analysis (pLSA)가 등장하였습니다.

4.2 pLSA 개념

pLSA는 확률 모델을 기반으로 문서 내 단어가 잠재적인 토픽(Latent Topics)에 의해 생성된다고 가정하는 기법입니다.
- 즉, 특정 문서에 포함된 단어는 해당 문서의 주제(토픽)로부터 확률적으로 생성된다는 구조를 따릅니다.

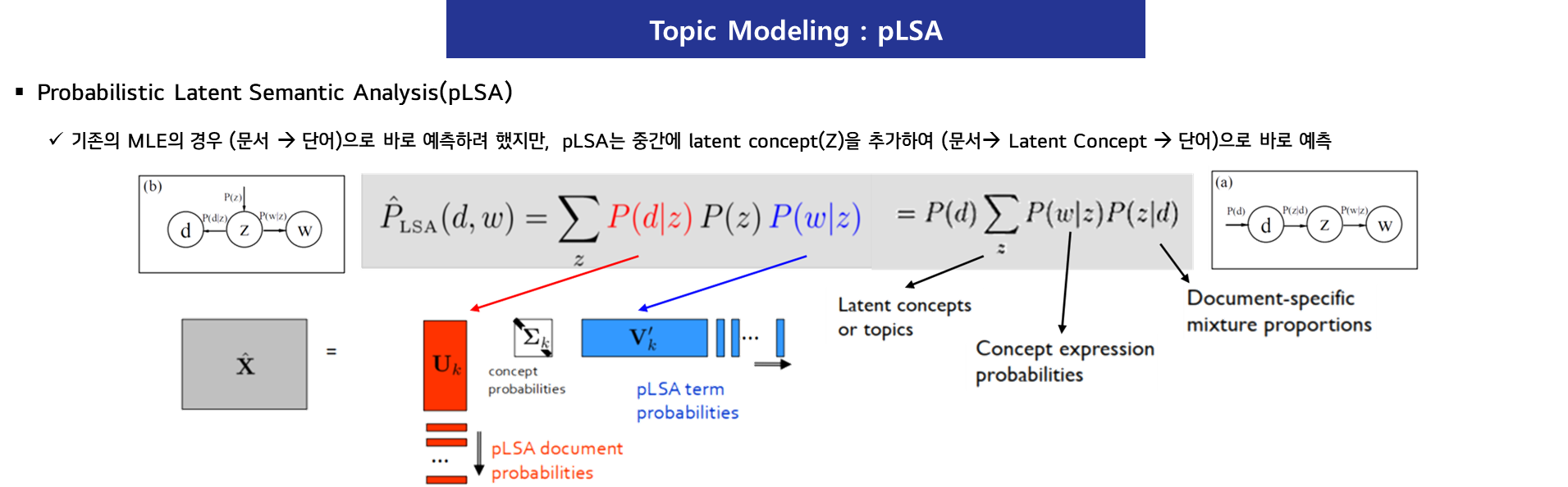
🙌 pLSA의 핵심 가정

문서는 여러 개의 토픽(Topic)으로 구성된다.

각 토픽은 특정 단어들의 확률 분포(Word Distribution)를 가진다.

각 단어는 특정 토픽에서 발생할 확률을 가지며, 문서 내 단어 분포는 이러한 토픽 분포의 혼합으로 표현된다.

pLSA의 확률 모델 구조

pLSA는 문서 $d$ 에서 단어 $w$ 가 발생할 확률을 아래와 같이 정의합니다.

P(w|d) = \sum_{z} P(z|d) P(w|z)

$P(z|d)$ : 문서 $d$ 가 특정 토픽 $z$ 를 포함할 확률
$P(w|z)$ : 특정 토픽 $z$ 에서 단어 $w$ 가 등장할 확률
$z$ : 잠재 토픽 (Latent Topic)

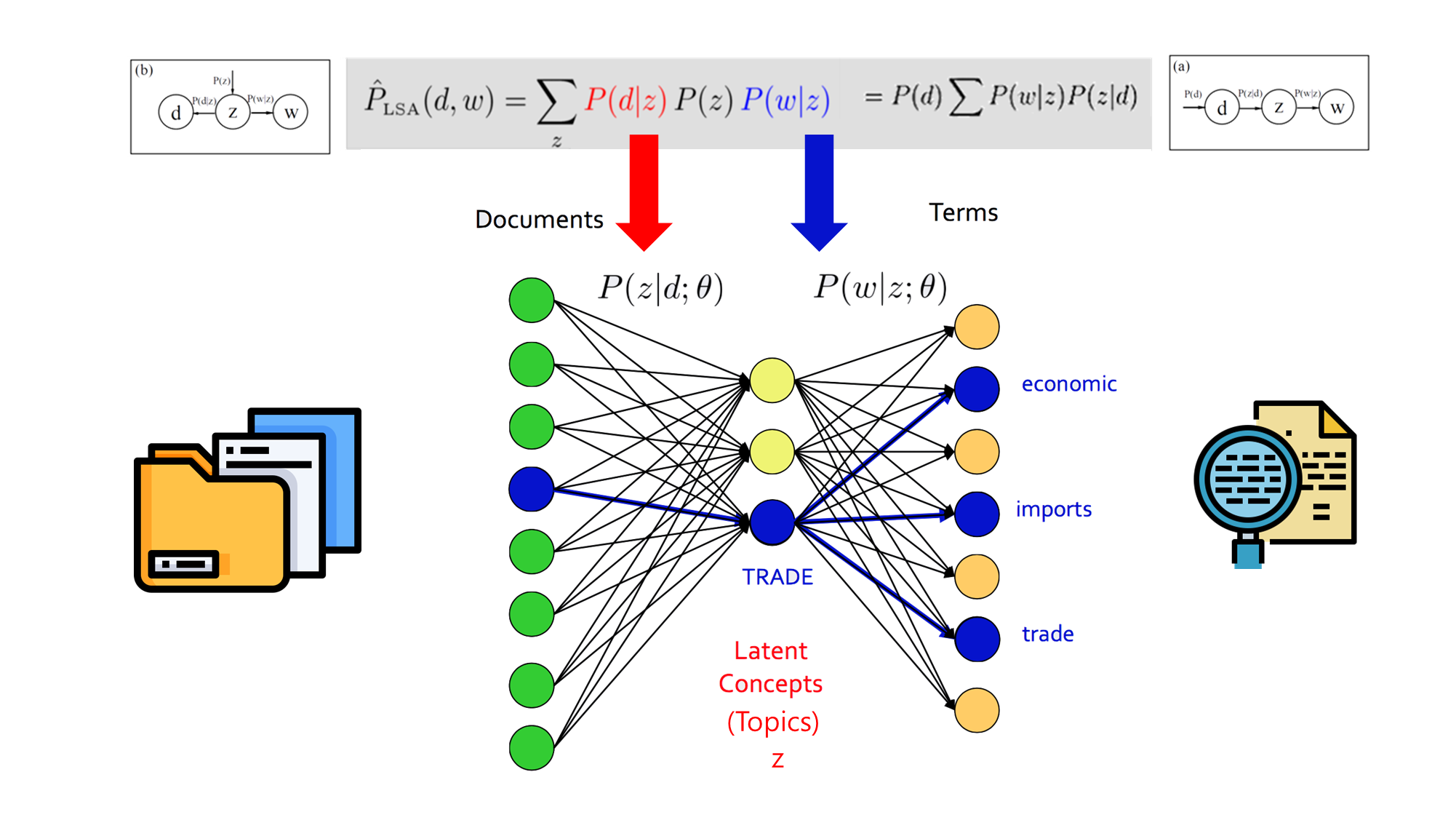
즉, 문서 내 단어는 문서의 토픽 분포와 토픽 내 단어 분포의 조합으로 생성됩니다.

4.3 pLSA의 학습 방법: EM 알고리즘

pLSA의 학습 과정은 Expectation-Maximization(EM) 알고리즘을 통해 수행됩니다.

🤔 Expectation-Maximization(EM) 알고리즘이란?
EM 알고리즘은 모수에 관한 추정값으로 로그가능도(log likelihood)의 기댓값을 계산하는 기댓값 (E) 단계와 이 기댓값을 최대화하는 모수 추정값들을 구하는 최대화 (M) 단계를 번갈아가면서 적용한다. 최대화 단계에서 계산한 변수값은 다음 기댓값 단계의 추정값으로 쓰인다.
출처 : wikipedia EM 알고리즘 (링크)

1) E-Step (Expectation Step)

E-Step에서는 현재의 모델 파라미터( $P(z|d)$ 와 $P(w|z)$ )를 사용하여 잠재 변수(Latent Variable)인 $P(z|d, w)$ 를 추정합니다.
- 이는 주어진 문서 $d$ 와 단어 $w$ 에 대해 특정 토픽 $z$ 가 선택될 확률을 계산하는 것입니다.
수식은 다음과 같습니다:

$P(z|d, w) = \frac{P(z|d) P(w|z)}{\sum_{z'} P(z'|d) P(w|z')}$
- $P(z|d)$ :
  - 문서 $d$ 에서 토픽 $z$ 가 선택될 확률
- $P(w|z)$ :
  - 토픽 $z$ 에서 단어 $w$ 가 생성될 확률
- $\sum_{z'} P(z'|d) P(w|z')$ :
  - 모든 가능한 토픽 $z'$ 에 대해 문서 $d$ 와 단어 $w$ 가 주어졌을 때의 확률의 합
이 단계에서는 현재의 모델 파라미터를 사용하여 각 단어가 특정 토픽에서 생성될 확률을 계산합니다.

2) M-Step (Maximization Step)

M-Step에서는 E-Step에서 계산된 $P(z|d, w)$ 를 사용하여 모델의 파라미터인 $P(z|d)$ 와 $P(w|z)$ 를 업데이트합니다.
- 문서-토픽 분포 $P(z|d)$ 업데이트:
  $P(z|d) = \frac{\sum_{w} n(w, d) P(z|d, w)}{\sum_{w, z} n(w, d) P(z|d, w)}$
- 토픽-단어 분포 $P(w|z)$ 업데이트:
  $P(w|z) = \frac{\sum_{d} n(w, d) P(z|d, w)}{\sum_{w', d} n(w', d) P(z|d, w')}$
여기서 $n(w, d)$ 는 문서 $d$ 에서 단어 $w$ 의 발생 횟수를 나타냅니다.
- $P(z|d)$ : 문서 $d$ 에서 토픽 $z$ 가 선택될 새로운 확률
- $P(w|z)$ : 토픽 $z$ 에서 단어 $w$ 가 생성될 새로운 확률
이 단계에서는 E-Step에서 계산된 $P(z|d,w)$ 를 사용하여 문서-토픽 분포와 토픽-단어 분포를 재계산합니다.

3) 반복 수행

E-Step과 M-Step을 반복적으로 수행하면서 모델의 로그 가능도(Log-Likelihood)가 수렴할 때까지 학습을 진행합니다.
- 로그 가능도는 모델이 주어진 데이터를 얼마나 잘 설명하는지를 나타내는 지표로, 이 값이 더 이상 크게 변하지 않으면 학습을 종료합니다.

💻 학습 과정 요약

Initialization:

$P(z|d)$ 와 $P(w|z)$ 를 임의의 값으로 초기화합니다.

E-Step (Expectation Step):

현재의 $P(z|d)$ 와 $P(w|z)$ 를 사용하여 $P(z|d, w)$ 를 계산합니다.

이는 전체 데이터를 사용하여 잠재 변수(Latent Variable)를 추정하는 과정입니다.

M-step (Maximization Step):

E-Step에서 계산된 $P(z|d, w)$ 를 사용하여 $P(z|d)$ 와 $P(w|z)$ 를 업데이트합니다.

이는 전체 데이터를 사용하여 파라미터를 최대화하는 과정입니다.

Iteration/Convergence:

종료/수렴할 때까지 E-Step과 M-Step을 반복적으로 수행합니다.

각 iteration은 전체 데이터를 사용하므로, 딥러닝의 epoch과 유사한 역할을 합니다.

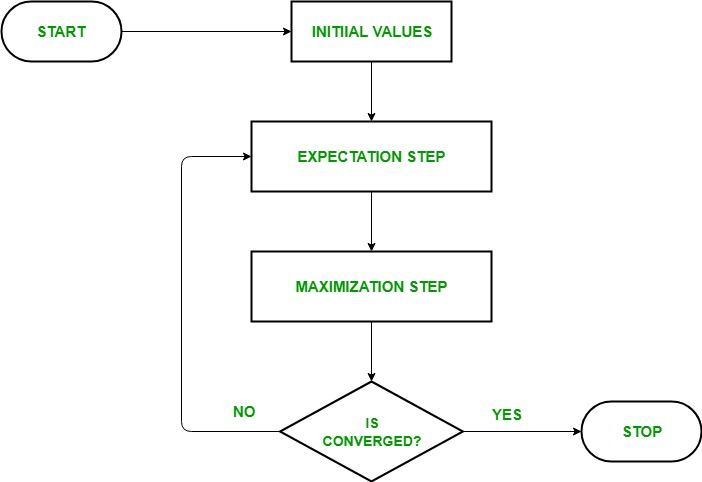
Image Source: https://www.geeksforgeeks.org/ml-expectation-maximization-algorithm/

4.4 pLSA의 장점

확률적 해석 가능
- 문서와 단어의 관계를 확률적인 방식으로 모델링하여 토픽과 단어 간의 의미적 관계를 효과적으로 파악 가능.
새로운 문서에 대한 일반화 가능
- LSA는 새로운 문서를 처리하기 어려웠지만, pLSA는 학습된 토픽-단어 분포 $P(w|z)$ 를 유지하면서 새로운 문서의 토픽 분포 $P(z|d)$ 를 추정할 수 있음.
언어 모델링에 더 적합한 구조
- 문서 내 단어 발생을 생성 모델(Generative Model)로 해석할 수 있어, 보다 자연스러운 문서 분류 및 정보 검색이 가능.

4.5 pLSA의 한계

오버피팅 문제
- pLSA는 각 문서 $d$ 에 대해 개별적인 확률 분포 $P(z|d)$ 를 학습해야 하므로, 문서 수가 증가할수록 모델의 파라미터 수도 비례하여 증가.
- 이는 데이터가 적을 경우 오버피팅(Overfitting) 문제를 일으킬 수 있음.
Bayesian 확률 모델이 아님
- pLSA는 단순한 최대우도추정(MLE, Maximum Likelihood Estimation)을 기반으로 학습하므로, 사전 확률(Prior Distribution) 적용이 어렵다.
- 즉, pLSA는 문서-토픽 분포 $P(z|d)$ 를 직접 최적화하는 방식이므로, 모델의 일반화 성능이 부족함.
LDA(Latent Dirichlet Allocation)의 등장
- 이러한 한계를 해결하기 위해 Latent Dirichlet Allocation(LDA)이 제안됨.
- LDA는 pLSA의 확장 모델로, 디리클레 분포(Dirichlet Distribution)를 사용하여 문서-토픽 분포를 정규화하여 오버피팅을 완화하고 일반화 성능을 향상.

5. Latent Dirichlet Allocation (LDA)

5.1 LDA의 등장 배경: 왜 pLSA에서 LDA로 발전했는가?

Probabilistic Latent Semantic Analysis(pLSA)는 기존의 LSA가 가지던 문제점(확률적 해석 불가능, 일반화 불가능, 계산량 문제)을 해결하는 데 기여했지만, 여전히 다음과 같은 한계를 지니고 있었습니다.

파라미터 수 증가 문제 (Overfitting)
- pLSA는 학습 데이터에 속한 문서마다 별도의 문서-토픽 분포 $P(z|d)$ 를 추정해야 합니다.
- 따라서 문서 수 $D$ 가 많아질수록 모델의 파라미터 수도 비례하여 증가하여, 과적합(Overfitting) 가능성이 높아집니다.
일반화 문제 (Lack of Generative Model)
- pLSA는 새로운 문서에 대한 확률 분포를 추론하기 어렵습니다.
- 학습 데이터에 없는 새로운 문서에 대해 $P(z|d)$ 를 바로 추정할 수 없기 때문에, 새로운 문서를 처리하려면 학습 과정을 다시 수행해야 합니다.
사전 확률(Prior) 부재
- pLSA는 순수한 최대우도추정(Maximum Likelihood Estimation, MLE)을 기반으로 학습되므로, 적절한 사전 확률(Prior Distribution)이 부재한 모델입니다.
- 이는 모델의 일반화 성능을 저하시킬 수 있으며, 불안정한 결과를 초래할 가능성이 있습니다.

이러한 문제를 해결하기 위해 Latent Dirichlet Allocation (LDA)이 제안되었습니다.

LDA는 베이지안 확률 모델(Bayesian Probabilistic Model)을 기반으로, 문서-토픽 분포와 토픽-단어 분포에 Dirichlet 분포(Dirichlet Prior)를 적용하여 모델의 일반화 성능을 높였습니다.

5.2 LDA 개념

LDA는 문서 내 단어가 여러 잠재적인 토픽(Latent Topics)에서 생성되었다고 가정하는 생성 모델(Generative Model)입니다.

즉, 문서는 여러 개의 토픽(Topic)으로 구성되며, 각 토픽은 특정 단어들의 확률 분포(Word Distribution)를 가진다고 가정합니다.

문서 생성의 가정:
- 각 문서는 하나 이상의 토픽이 혼합된 형태로 존재하며, 각 단어는 해당 문서의 토픽들 중 하나에서 생성됨.
- 각 토픽은 특정 단어들의 확률 분포를 가지며, 단어가 특정 토픽에서 발생할 확률을 학습.
문제 해결 목표:
- 주어진 문서 집합(Corpus)에서 각 문서가 어떤 토픽을 포함하는지를 추정.
- 각 문서에 포함된 토픽 분포( $\theta_d$ ) 및 각 토픽에서 등장하는 단어 분포( $\phi_k$ )를 추론.
- 특정 문서 내에서 각 단어가 어떤 토픽에 할당되었는지 추정.

5.3 LDA의 문서 생성 과정

LDA는 문서가 아래와 같은 절차를 통해 생성된다고 가정합니다.

1) 초기 설정

토픽 분포 ( $\theta_d$ )
- 문서 $d$ 의 토픽 분포는 Dirichlet 분포 $Dir(\alpha)$ 에서 샘플링.
단어 분포 ( $\phi_k$ )
- 토픽 $k$ 의 단어 분포는 Dirichlet 분포 $Dir(\beta)$ 에서 샘플링.

2) 문서 생성 절차

문서 $d$ 에 대해, 토픽 분포 $\theta_d$ 를 Dirichlet 분포 $Dir(\alpha)$ 에서 샘플링.
각 단어 $w_{dn}$ 에 대해:
- 토픽 $z_{dn}$ 선택: 문서의 토픽 분포 $\theta_d$ 에서 샘플링.
- 단어 $w_{dn}$ 선택: 선택된 토픽 $z_{dn}$ 의 단어 분포 $\phi_{z_{dn}}$ 에서 샘플링.

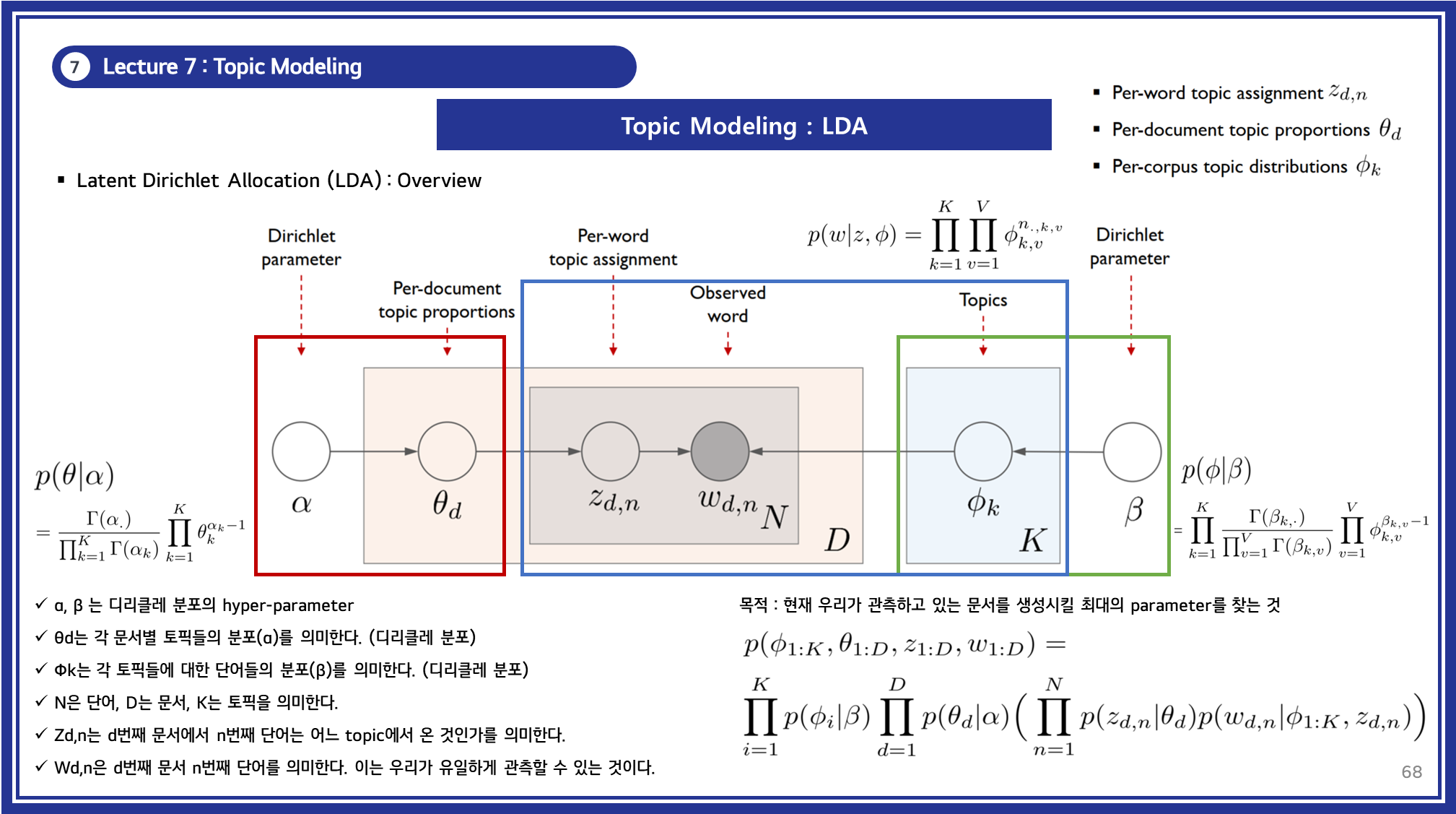
3) 수학적 표현

LDA의 전체 문서 생성 과정은 확률적으로 다음과 같이 표현됩니다:

P(W, Z, \theta, \phi | \alpha, \beta) = \prod_{d=1}^{D} P(\theta_d | \alpha) \prod_{k=1}^{K} P(\phi_k | \beta) \prod_{n=1}^{N_d} P(z_{dn} | \theta_d) P(w_{dn} | \phi_{z_{dn}})

$W$ : 단어 집합
$Z$ : 단어의 토픽 할당
$\theta$ : 문서의 토픽 분포
$\phi$ : 토픽의 단어 분포

5.4 LDA의 학습 및 추론

LDA의 주요 문제는 관측된 단어 $W$ 만을 기반으로 잠재 변수 $\theta, \phi, Z$ 를 추정하는 것입니다.

이를 해결하기 위해 LDA에서는 다음과 같은 학습 방법이 사용됩니다.

1) Collapsed Gibbs Sampling

LDA에서 가장 널리 사용되는 추론 기법으로, 단어-토픽 할당 변수 $Z$ 를 샘플링하여 $\theta$ 와 $\phi$ 를 추정합니다.
조건부 확률을 기반으로 샘플링을 수행하며, 다음과 같은 과정을 반복하여 최적화합니다.

P(z_{dn} = k | Z_{-dn}, W, \alpha, \beta) \propto \frac{n_{d,k}^{-dn} + \alpha}{\sum_{k'} (n_{d,k'}^{-dn} + \alpha)} \cdot \frac{n_{k,w}^{-dn} + \beta}{\sum_{w'} (n_{k,w'}^{-dn} + \beta)}

$n_{d,k}^{-dn}$ : 문서 $d$ 에서 토픽 $k$ 가 할당된 단어의 수 (현재 단어 제외)
$n_{k,w}^{-dn}$ : 토픽 $k$ 에서 단어 $w$ 가 등장한 횟수 (현재 단어 제외)

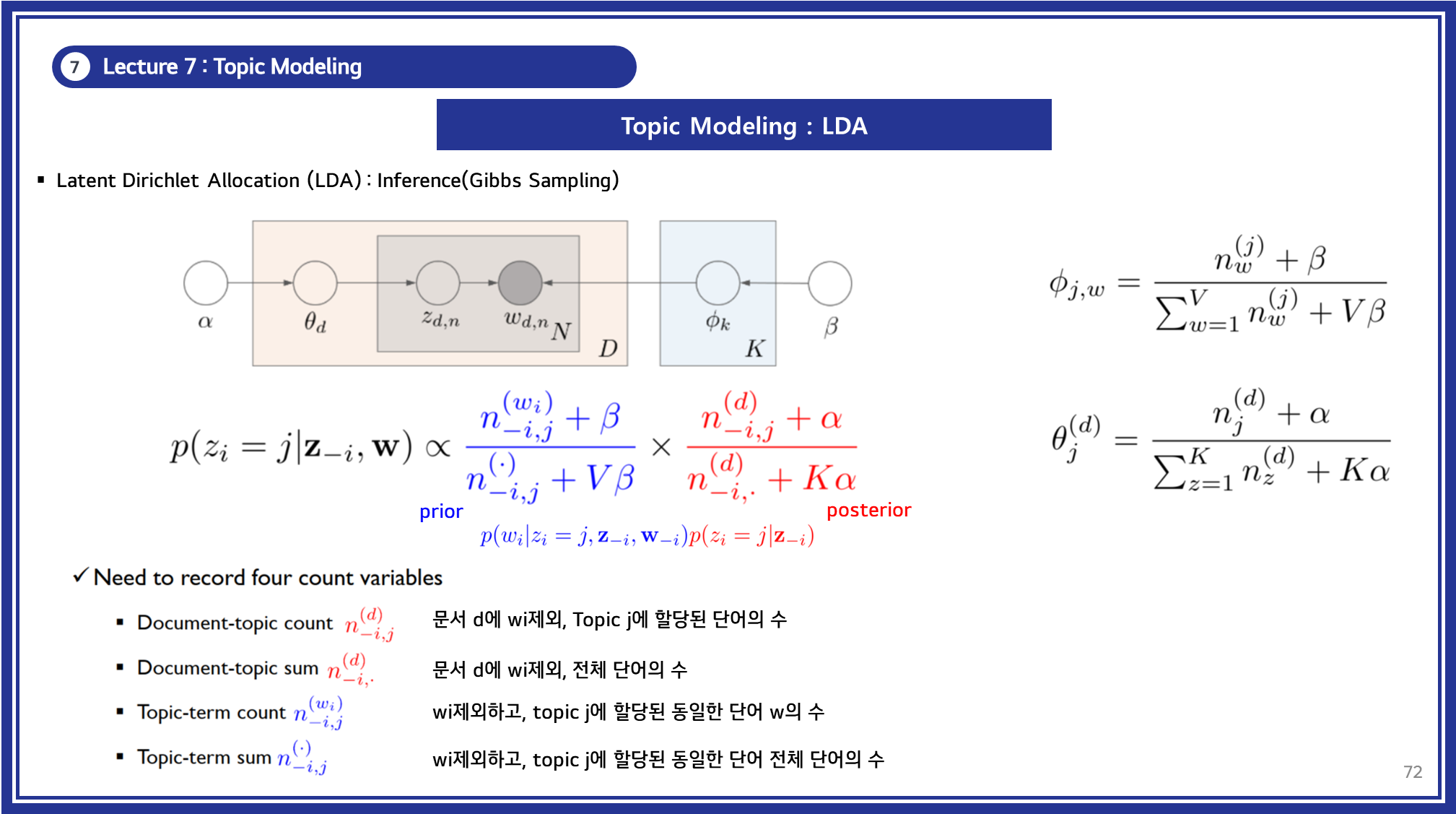
2) Variational Inference

Gibbs Sampling보다 빠른 근사 추론 방법으로, ELBO(Evidence Lower Bound)를 최대화하는 방식.
LDA를 확률적 그래프 모델로 해석하여 변분 분포 $q(\theta, \phi, Z)$ 를 최적화.

5. 결론

Topic Modeling은 비정형 텍스트 데이터를 구조화하고 의미를 발견하는 강력한 기법으로, 문서 내 숨겨진 주제를 효과적으로 추출할 수 있습니다.

LSA, pLSA, LDA와 같은 대표적인 기법들은 각각의 특성과 한계를 가지며, 활용 목적과 데이터 특성에 따라 적절한 방법을 선택하는 것이 중요합니다.
- LSA는 선형 대수 기반 행렬 분해 기법으로 계산이 빠르고 직관적이지만, 확률적 해석이 어렵고 새로운 문서 처리에 한계가 있습니다.
- pLSA는 확률 모델을 도입하여 문서 내 토픽 분포를 보다 정교하게 모델링하지만, 오버피팅 문제와 일반화의 어려움이 존재합니다.
- LDA는 베이지안 추론을 활용하여 문서와 토픽의 관계를 확률적 모델링하며, 일반화 성능이 우수하고 다양한 변형 모델이 개발되면서 더욱 강력한 성능을 발휘하고 있습니다.
Topic Modeling에서 핵심적인 요소는 적절한 토픽 개수 설정이며, 토픽 개수가 적절하지 않으면 과적합(Overfitting) 혹은 의미적 혼란이 발생할 수 있습니다.
- Perplexity, Coherence Score, Human Evaluation 등의 방법을 활용하여 최적의 토픽 개수를 결정하는 것이 중요합니다.

최근 연구에서는 LDA를 기반으로 한 변형 모델들이 등장하면서 성능이 더욱 향상되고 있습니다.

읽어주셔서 감사합니다 😎

서쿠

Always be passionate ✨

이전 포스트

[NLP] 6. Topic Modeling이란?

NLP 강의요약

1. Topic Modeling이란?

2. Topic Modeling의 접근법

2.1 행렬 분해 기반(Matrix Factorization) 접근

2.2 확률 모델(Probabilistic Model) 기반 접근

3. Latent Semantic Analysis (LSA)

3.1. Latent Structure (잠재 구조)

3.2. Matrix Decomposition (행렬 분해)

3.3. LSA (Latent Semantic Analysis)

3.4 LSA의 특징

3.5 LSA의 실습

4. Probabilistic Latent Semantic Analysis (pLSA)

4.1 pLSA의 등장 배경

4.2 pLSA 개념

4.3 pLSA의 학습 방법: EM 알고리즘

4.4 pLSA의 장점

4.5 pLSA의 한계

5. Latent Dirichlet Allocation (LDA)

5.1 LDA의 등장 배경: 왜 pLSA에서 LDA로 발전했는가?

5.2 LDA 개념

5.3 LDA의 문서 생성 과정

5.4 LDA의 학습 및 추론

5. 결론

[NLP] 5. 자연어 차원 축소(Dimension Reduction) 기법

0개의 댓글

관련 채용 정보