[NLP] 5. 자연어 차원 축소(Dimension Reduction) 기법

서쿠·2025년 1월 28일

NLP 강의노트

NLP 강의요약

목록 보기

5/6

차원 축소 (Dimensionality Reduction)

본 강의는 DSBA 강필성 교수님의 강의를 참조하여 작성되었습니다.

1. 차원 축소란 무엇인가?

차원 축소는 고차원의 데이터를 저차원의 데이터로 변환하는 기법입니다.

이를 통해 계산 효율성을 높이고, 데이터 분석 및 시각화를 용이하게 할 수 있습니다.

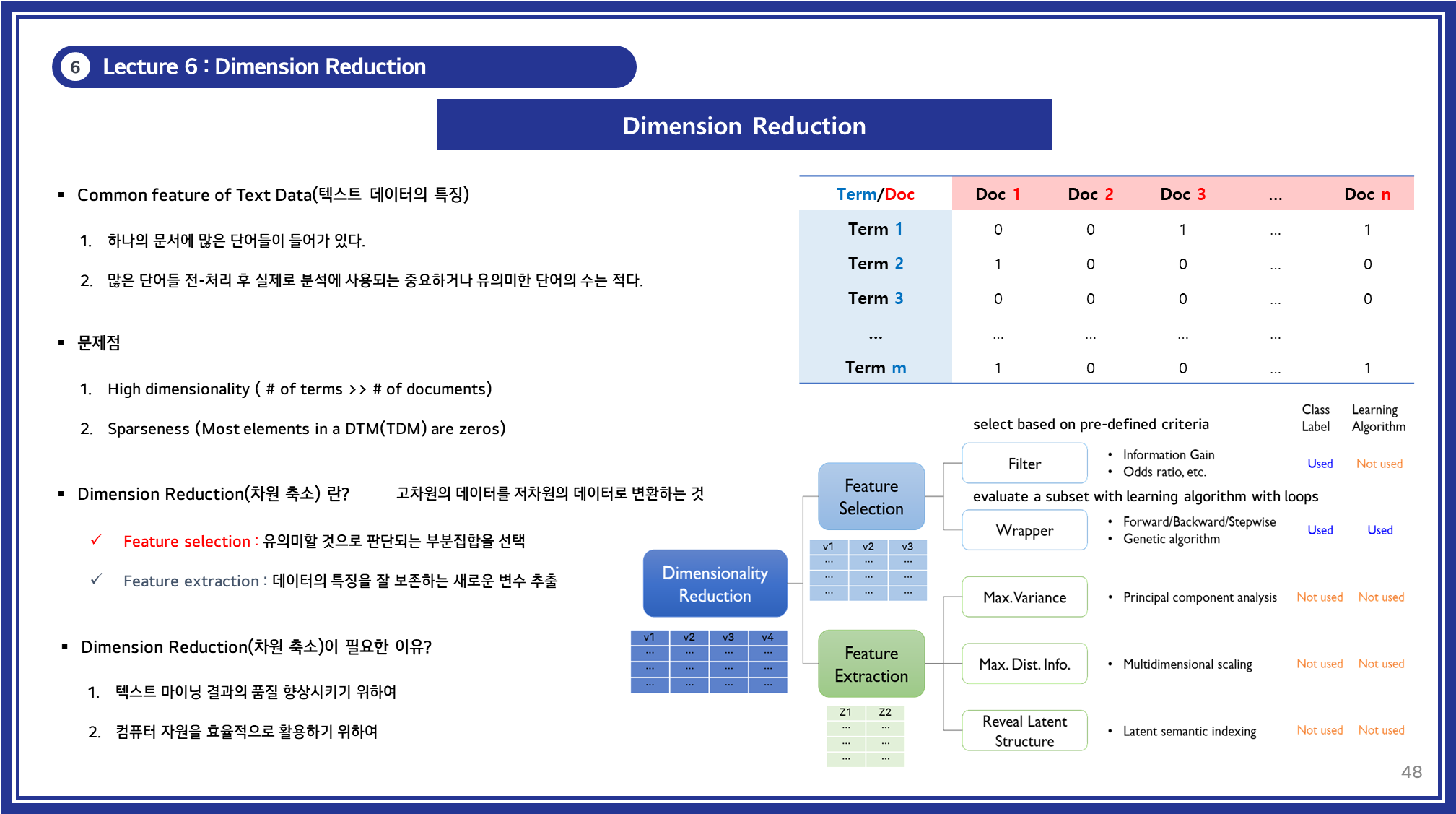
차원 축소는 다음 두 가지로 분류됩니다:

특징 선택(Feature Selection): 중요하지 않은 특성을 제거하여 데이터를 간소화합니다.
특징 추출(Feature Extraction): 데이터의 특성을 잘 보존하는 새로운 변수를 추출합니다.

강의에서는 차원 축소의 정의와 함께, 텍스트 데이터의 다음과 같은 특징을 강조하였습니다:

하나의 문서에 많은 단어들이 포함된다.
대부분의 단어가 전처리 후 분석에 사용되지 않는다.

1.1 텍스트 데이터의 문제점

고차원성: 용어(term)의 수가 문서(document)의 수보다 훨씬 많습니다.
희소성: 대부분의 요소가 0인 희소 행렬(Sparse Matrix) 형태를 가집니다.

1.2 차원 축소가 필요한 이유

텍스트 마이닝 결과의 품질을 높이기 위해
컴퓨터 자원의 효율적 활용을 위해

2. Feature Selection(특징 선택)

특징 선택은 데이터를 구성하는 많은 변수 중에서 유의미한 변수만을 선택하는 과정입니다.

강의에서는 다음 10가지 특징 선택 지표를 소개하였습니다:

Document Frequency (DF): 특정 단어가 문서에 등장하는 수.
Accuracy: 특정 단어가 특정 클래스의 문서에 등장하는 정확도.
Accuracy Ratio: 클래스 간 정확도의 비율 차이.
Probability Ratio: 클래스 간 확률의 비율.
Odds Ratio: 성공할 확률과 실패할 확률의 비율.
Odds Ratio Numerator: Odds Ratio의 분자를 단순화한 값.
F1-Measure: Recall과 Precision의 조화 평균.
Information Gain: 단어가 제공하는 정보량.
Chi-squared Statistic: 단어 등장 빈도와 클래스 간 독립성의 통계적 테스트.
Bi-Normal Separation: 클래스 간 분포 차이.

각 지표는 데이터의 특성을 분석하여 더 나은 모델링 결과를 얻기 위해 활용됩니다.

3. Feature Extraction(특징 추출)

특징 추출은 기존 데이터를 변환하여 새로운 저차원의 데이터를 생성하는 방법입니다. 강의에서는 다음 세 가지 주요 기법을 다루었습니다:

3.1 Singular Value Decomposition (SVD)

SVD는 행렬을 세 개의 행렬(U, Σ, Vᵀ)로 분해하여 데이터를 저차원으로 변환합니다. 이를 통해 데이터의 주요 패턴을 유지하며 차원을 축소할 수 있습니다.

강의에서는 SVD의 다음과 같은 특징이 설명되었습니다:

U와 V는 직교 행렬이며, Σ는 대각 행렬입니다.
Σ의 대각 원소는 데이터의 중요도를 나타냅니다.
축소된 SVD를 통해 주요한 성분만을 선택할 수 있습니다.

SVD는 데이터의 구조를 이해하고, 불필요한 정보를 제거하여 데이터 분석의 효율성을 극대화합니다.

3.2 Latent Semantic Analysis (LSA)

LSA는 SVD를 사용하여 텍스트 데이터의 잠재 의미를 추출하는 기법입니다.

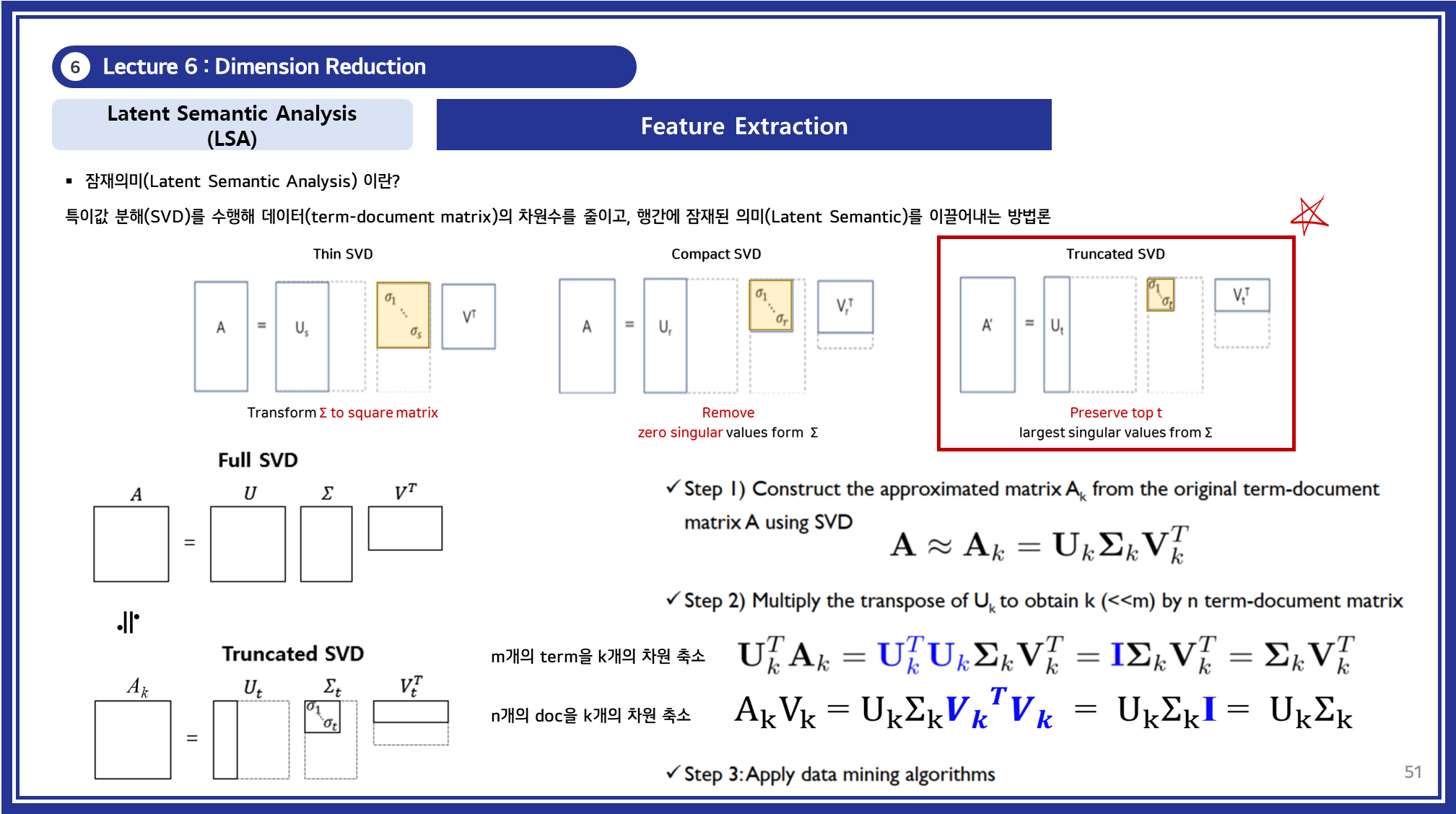
강의에서는 다음 단계를 다루었습니다:

SVD를 통해 행렬 A를 분해합니다.
주요한 k개의 특이값만을 남겨 저차원 행렬을 생성합니다.
생성된 저차원 행렬을 통해 데이터 마이닝 알고리즘을 적용합니다.

LSA는 텍스트 데이터의 의미론적 구조를 추출하여 검색 엔진 및 추천 시스템에서 중요한 역할을 합니다.

3.3 Stochastic Neighbor Embedding (SNE)

SNE는 고차원 데이터에서 데이터 간의 가까운 이웃 관계를 저차원에서도 유지하며 변환하는 차원 축소 기법입니다. 이는 고차원 공간에서 데이터 포인트 간의 유사도를 확률적으로 표현하고, 저차원 공간에서도 이 확률 분포를 최대한 보존하도록 데이터를 매핑하는 방식입니다.

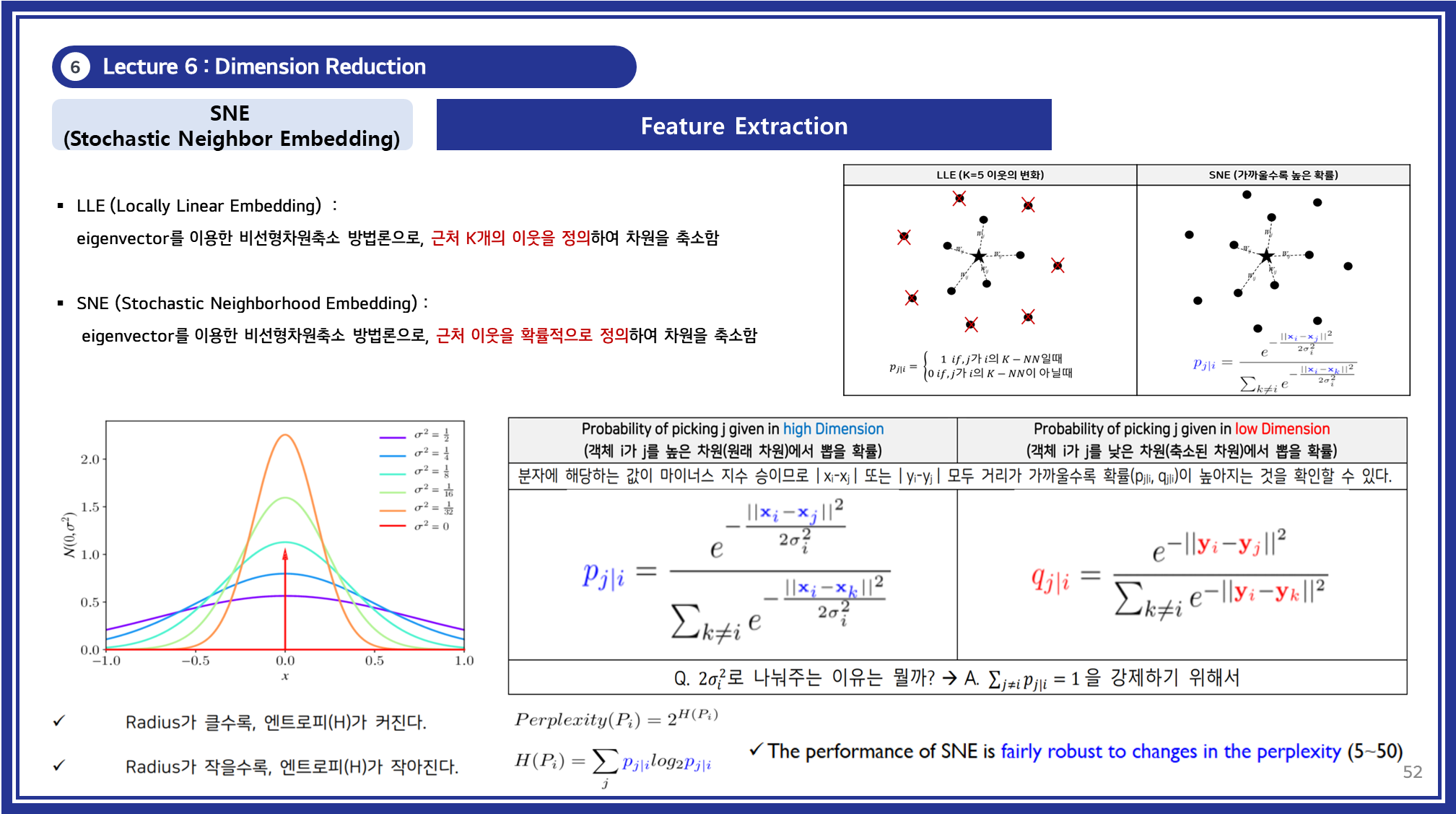
강의에서는 다음과 같은 SNE의 주요 개념을 소개하였습니다:

고차원 공간의 확률적 유사도 정의: 고차원 데이터에서 각 데이터 포인트가 다른 포인트를 가까운 이웃으로 선택할 확률을 정의합니다. 이 확률은 가우시안 분포를 기반으로 계산됩니다.
저차원 공간의 유사도 매핑: 저차원 공간에서도 유사도를 동일한 방식으로 정의하여 고차원 공간의 확률 분포와 최대한 일치하도록 데이터를 배치합니다.
비용 함수 최적화: 고차원과 저차원 확률 분포 간의 차이를 최소화하기 위해 Kullback-Leibler(KL) 발산을 비용 함수로 사용합니다.

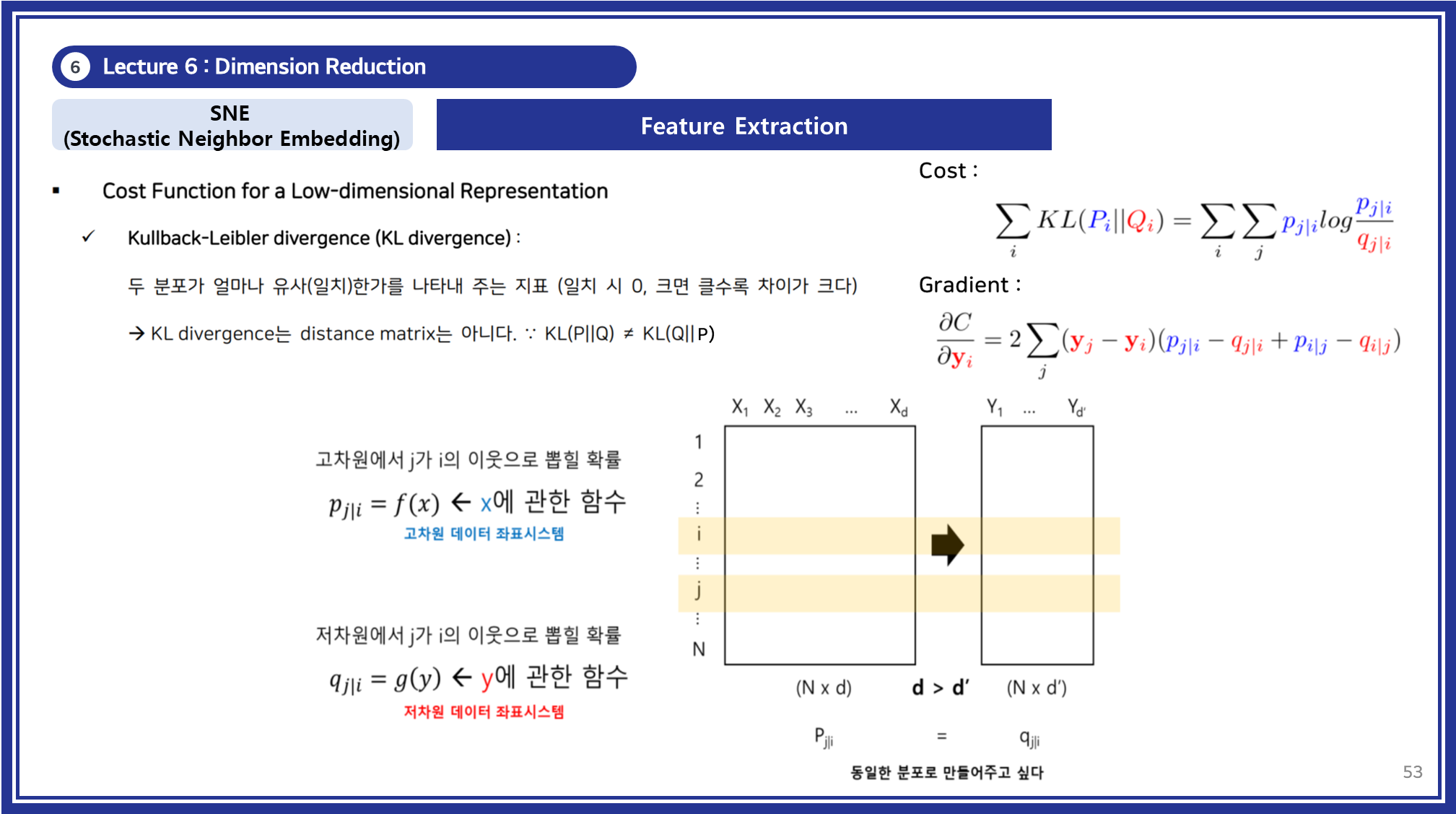
SNE의 한계점: 기존 SNE는 데이터가 밀집될수록 저차원에서의 분포가 왜곡되는 "Crowding Problem"을 겪습니다. 이는 고차원에서 넓게 퍼져 있는 데이터가 저차원으로 축소될 때, 중심으로 몰리는 경향 때문입니다.

(참고) Locally Linear Embedding (LLE)

LLE는 SNE와 달리, 각 데이터 포인트를 이웃 포인트의 선형 결합으로 표현하여 고차원 데이터의 로컬 구조를 보존하는 방식입니다. 다음은 강의에서 소개된 LLE의 주요 특징입니다:

로컬 구조 보존: 각 데이터 포인트는 이웃 데이터 포인트들의 선형 조합으로 표현되며, 이 관계를 저차원에서도 유지합니다.
효율적인 계산: 확률 대신 선형 결합 계수를 활용하므로 계산 효율성이 높습니다.
비선형 관계 표현: 고차원 데이터의 복잡한 패턴을 효과적으로 분석할 수 있습니다.

SNE와 LLE의 관계
강의에서는 SNE와 LLE가 각각 독립적으로 제안된 기법임을 명확히 하였습니다. SNE가 LLE를 극복하거나 대체하기 위해 개발된 것은 아니며, 두 기법은 서로 다른 접근법과 목적을 가집니다:

SNE: 확률 기반 접근으로 데이터 포인트 간의 유사도를 보존.
LLE: 선형 관계 기반 접근으로 로컬 구조를 보존.

LLE는 특히 데이터의 지역적 구조를 강조하며, SNE는 데이터 간의 전체적인 유사도를 시각화하거나 클러스터링 구조를 탐색하는 데 적합합니다.

Symmetric SNE와 t-SNE
강의에서는 Crowding Problem을 극복하기 위한 두 가지 개선된 버전을 다루었습니다:

Symmetric SNE: 대칭적인 확률 분포를 사용하여 기존 SNE의 표현 신뢰성을 높였습니다. 이를 통해 저차원에서의 데이터 간 상대적인 유사도를 더 정확히 반영할 수 있습니다.
t-SNE: t-분포를 사용하여 Crowding Problem을 효과적으로 해결한 버전입니다. t-SNE는 고차원 데이터의 클러스터링 구조를 더 명확히 드러내고, 클러스터 간의 경계를 강조하여 데이터 시각화에서 널리 활용됩니다.

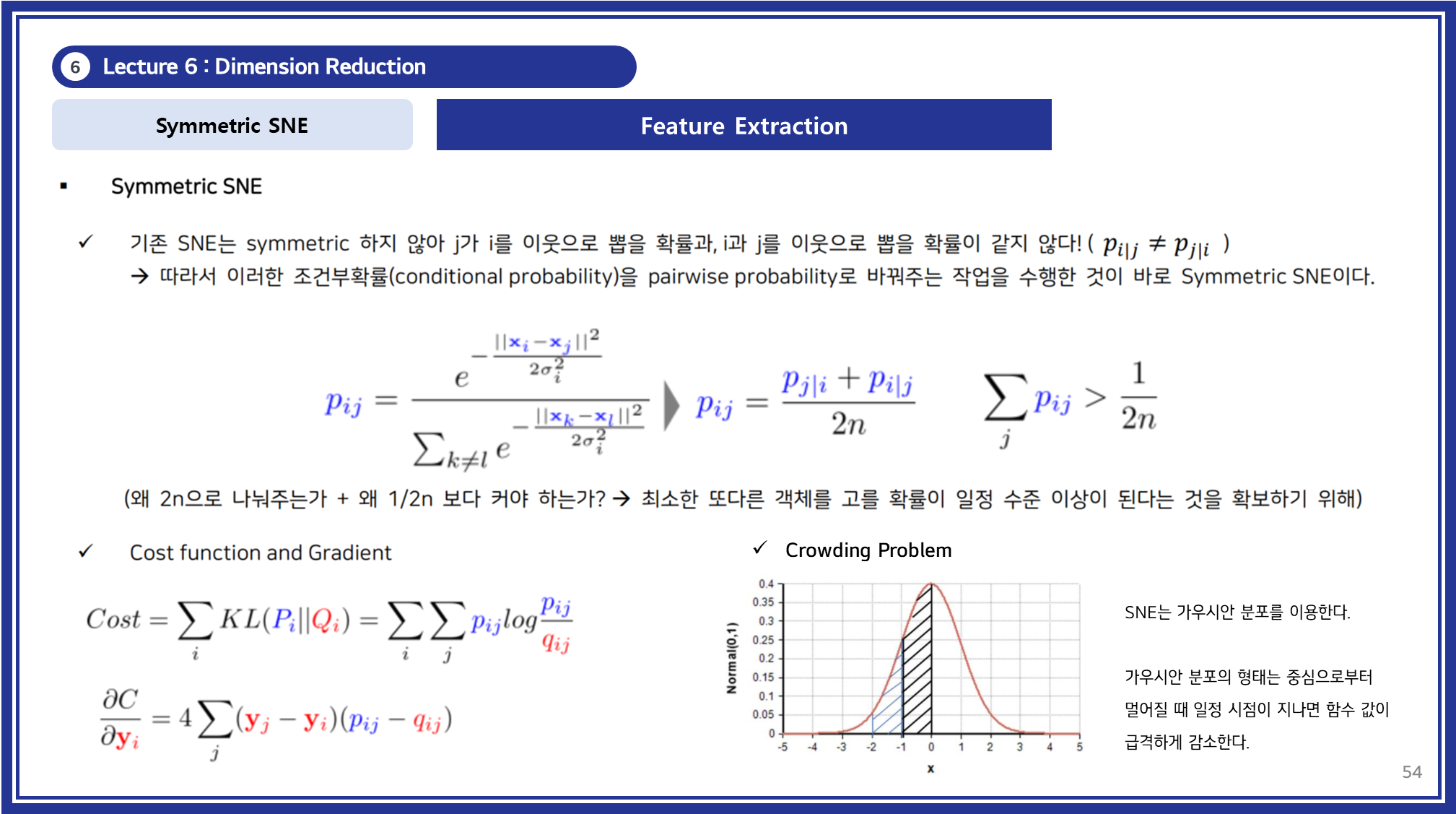
Symmetric SNE

Symmetric SNE는 기존 SNE에서 발생하는 비대칭적인 확률 계산 문제를 해결하기 위해 고안된 개선된 차원 축소 기법입니다.

기존 SNE에서는 고차원에서 각 데이터 포인트 $i$ 가 다른 데이터 포인트 $j$ 를 이웃으로 선택할 확률 $p_{j|i}$ 를 계산하는 방식이었으나, Symmetric SNE는 이러한 조건부 확률 대신 대칭적 확률 $p_{ij}$ 를 정의하여 표현합니다.
이를 통해 고차원 공간과 저차원 공간의 확률 분포 간 일관성을 강화합니다.

주요 특징

대칭적 확률 정의:
- Symmetric SNE는 $p_{ij} = \frac{p_{j|i} + p_{i|j}}{2n}$ 로 확률을 정의하여 확률 값이 대칭성을 가지도록 설정합니다.
- 이러한 방식은 저차원 공간에서의 데이터 간 관계를 더 균일하게 표현하며, 기존 SNE 대비 계산적 안정성을 제공합니다.
비용 함수 및 최적화:
- 비용 함수는 여전히 $Kullback-Leibler(KL)$ 발산을 사용하나, 대칭적 확률 분포를 기반으로 최적화가 진행됩니다.
- 이는 고차원과 저차원의 데이터 분포 차이를 효과적으로 줄이며, 데이터 표현의 신뢰성을 높입니다.

한계점

Symmetric SNE는 기존 SNE의 Crowding Problem을 완전히 해결하지는 못하며, 저차원에서의 데이터 밀도 왜곡은 여전히 존재할 수 있습니다. 이러한 문제를 보완하기 위해 t-SNE가 도입되었습니다.

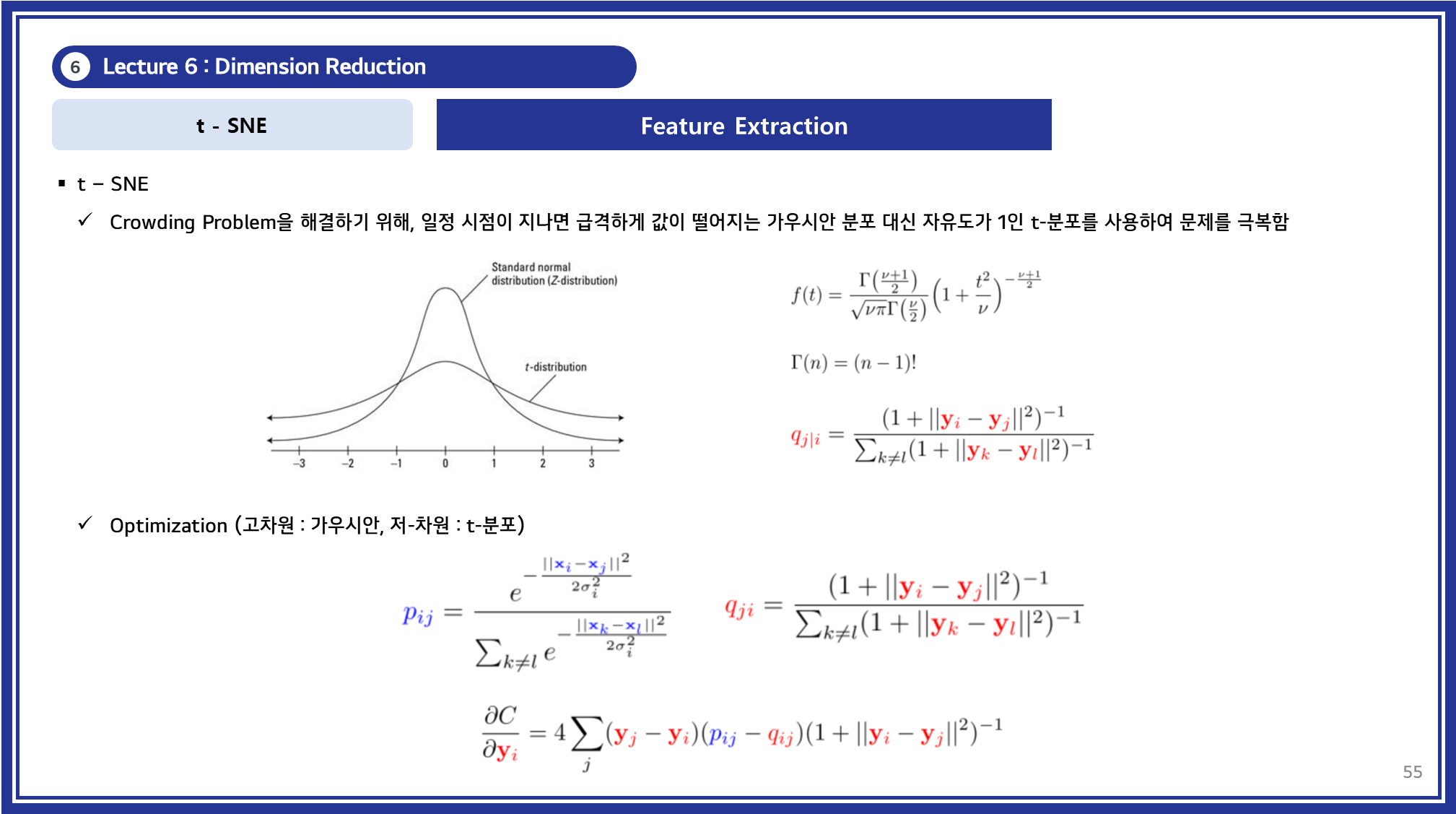
t-SNE

t-SNE(t-distributed Stochastic Neighbor Embedding)는 Symmetric SNE에서 더 나아가 Crowding Problem을 해결하기 위해 제안된 기법으로, 저차원에서의 데이터 분포를 더욱 자연스럽게 표현합니다.

특히, 고차원 데이터의 클러스터링 구조를 명확히 드러내는 데 탁월한 성능을 보입니다.

주요 특징

t-분포 기반 확률 정의:
- 저차원 공간에서의 유사도 계산에 t-분포를 적용하여 데이터 간 거리가 멀어질수록 유사도가 급격히 감소하지 않도록 설계되었습니다.
- 이는 고차원에서의 데이터 간 거리와 저차원 간 거리가 불균형하게 표현되는 문제를 해결합니다.
데이터 시각화에 최적화:
- 고차원 데이터의 클러스터 간 경계를 강조하며, 저차원 공간에서 데이터를 효과적으로 분리합니다.
- 특히, 데이터 점들이 고유한 패턴을 나타내도록 저차원에 배치되기 때문에 시각적으로 직관적인 결과를 제공합니다.
비용 함수 및 최적화:
- 비용 함수는 KL 발산을 기반으로 하며, 고차원과 저차원의 확률 분포 차이를 최소화합니다.
- 최적화 과정에서는 t-분포의 특성을 활용해 데이터의 구조를 저차원 공간에서 효과적으로 재현합니다.

한계점

t-SNE는 데이터의 전체적인 구조를 유지하기보다는 지역적 구조(Local Structure)를 강조하는 경향이 있습니다.

또한, 데이터 크기가 커질수록 계산 비용이 증가하며, 초기 설정(예: 퍼플렉시티 값)에 따라 결과가 달라질 수 있습니다.

결론

이번 강의는 차원 축소의 중요성과 이를 구현하는 다양한 방법론을 심도 있게 다뤘습니다.

특히, Feature Selection과 Feature Extraction이라는 두 가지 큰 축을 중심으로 다양한 기법의 특성과 적용 사례를 비교 분석했습니다.

Feature Selection은 고차원의 데이터를 효율적으로 줄이기 위해 불필요한 변수를 제거하며, 모델의 성능을 향상시키는 데 기여합니다.
Feature Extraction은 기존 데이터를 저차원의 표현으로 변환하며, SVD와 LSA를 통해 잠재 의미를 추출하거나, SNE와 t-SNE를 통해 데이터 간의 관계를 효과적으로 시각화할 수 있습니다.

또한, SNE와 그 개선 버전인 Symmetric SNE 및 t-SNE는 데이터의 전체적인 유사도를 유지하면서 클러스터 간 경계를 강조하는 데 강점을 보입니다.

이는 데이터 시각화와 고차원 데이터의 탐색에 매우 유용하며, Crowding Problem과 같은 기존 한계를 극복하는 데 중요한 역할을 합니다.

마지막으로, LLE와 SNE가 서로 다른 목적과 접근법을 가진 독립적인 기법임을 이해하고, 각각의 장단점을 파악하여 적절히 활용하는 것이 중요합니다. 차원 축소 기법의 선택은 분석 목표와 데이터의 특성에 따라 달라져야 하며, 이를 바탕으로 더 나은 분석과 모델링 결과를 기대할 수 있습니다.