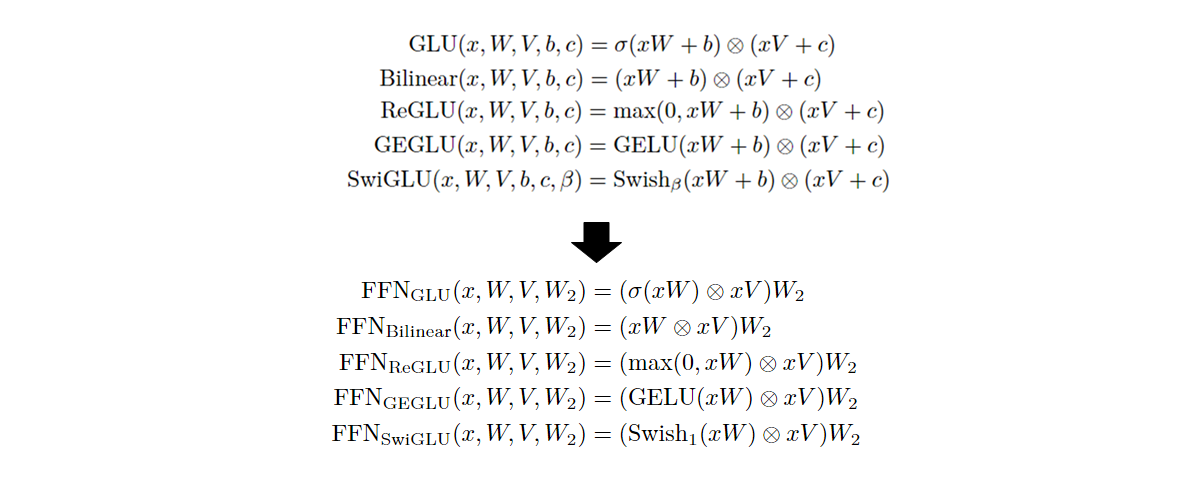[개념] GLU와 그 변형들: 역사와 주요 개념 정리

서쿠·2024년 10월 14일

딥러닝 분야에서 활성화 함수는 신경망 모델이 학습할 때 중요한 역할을 합니다. 이 중에서도 GLU(Gated Linear Unit)는 고급 모델에서 자주 사용되는 활성화 함수 중 하나입니다.

특히 자연어 처리(NLP)와 같은 분야에서 뛰어난 성능을 발휘하며, 이 활성화 함수에서 파생된 여러 변형들이 연구되었습니다. 이번 글에서는 GLU와 그 변형들, 그리고 각 변형의 발전 과정을 따라가며 그 개념과 중요성을 설명하고자 합니다.

📋 (참고) GLU Variants Improve Transformer
✔ 이번 포스팅을 쓰면서 참고한 논문인데, Transformer 모델에서 Gated Linear Units (GLU) 및 Variants을 사용하여 모델 성능을 개선하는 방법에 대해 연구한 논문입니다.

아래는 링크 및 주요 내용 요약입니다. 😎

링크 : https://arxiv.org/pdf/2002.05202

Transformer 모델은 시퀀스-투-시퀀스 변환 작업에 널리 사용되는 모델로, 다중 헤드 주의 메커니즘과 위치별 피드포워드 네트워크(FFN)를 교대로 사용하는 구조를 가지고 있습니다.

FFN은 입력 벡터를 두 개의 선형 변환을 거쳐 처리하며, 중간에 ReLU 활성화 함수를 사용합니다.

기존의 FFN 구조에서는 ReLU 외에도 다른 활성화 함수(GELU, Swish 등)를 사용할 수 있으며, 이 논문에서는 GLU 및 그 변형을 FFN에 적용하여 성능 개선을 시도합니다.

저자들은 다양한 GLU 변형을 Transformer 기반의 Text-to-Text Transfer Transformer(T5) 모델에 적용하여 실험을 진행했습니다.

이를 통해 새로운 FFN 변형들이 기존 FFN 구조에 비해 더 나은 성능을 보인다는 것을 입증했습니다.

(참고) Activation Functions

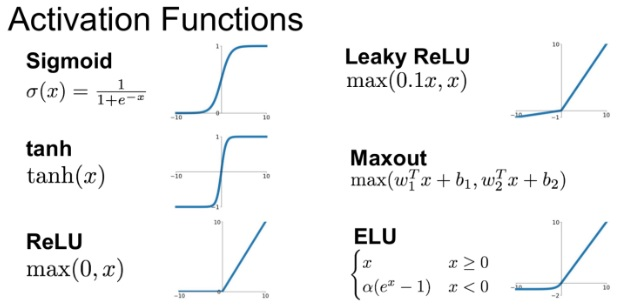
아래 개념 및 이미지 출처: https://paperswithcode.com/method

Sigmoid

소개 시기: 1960년대
수학적 정의: $\sigma(x) = \frac{1}{1 + e^{-x}}$
등장 배경: 신경망의 초기 모델에서 사용되었으며, 출력을 0과 1 사이로 제한하여 확률로 해석할 수 있게 합니다.

Tanh (Hyperbolic Tangent)

소개 시기: 1990년대
수학적 정의: $\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$
등장 배경: Sigmoid의 대안으로 제안되었으며, 출력 범위가 -1에서 1 사이로 중심이 0이라는 장점이 있습니다.

ReLU (Rectified Linear Unit)

소개 시기: 2010년
수학적 정의: $f(x) = \max(0, x)$ 등장 배경: 기울기 소실 문제를 해결하고 계산 효율성을 높이기 위해 도입되었습니다.

Leaky ReLU

소개 시기: 2013년
수학적 정의: $f(x) = \max(0.01x, x)$
등장 배경: ReLU의 "죽은 뉴런" 문제를 해결하기 위해 제안되었습니다.

Maxout

소개 시기: 2013년
수학적 정의: $f(x) = \max(w_1^Tx + b_1, w_2^Tx + b_2)$
등장 배경: ReLU의 일반화된 형태로, 더 강력한 특징 학습을 위해 제안되었습니다.

ELU (Exponential Linear Unit)

소개 시기: 2015년
수학적 정의: $f(x) = \begin{cases} x & \text{if } x > 0 \\ \alpha(e^x - 1) & \text{if } x \leq 0 \end{cases}$
등장 배경: ReLU의 장점을 유지하면서 음수 입력에 대한 처리를 개선하기 위해 제안되었습니다.

GELU (Gaussian Error Linear Unit)

소개 시기: 2016년
수학적 정의:
$\text{GELU}(x) = x \cdot \Phi(x)$
- 여기서 $\Phi(x)$ 는 표준 정규 분포의 누적 분포 함수입니다.
등장 배경: 자연어 처리 태스크에서 우수한 성능을 보이기 위해 개발되었습니다.

Mish

소개 시기: 2019년
수학적 정의: $f(x) = x \cdot \tanh(\ln(1 + e^x))$
등장 배경: 자기 정규화 특성과 부드러운 기울기를 가지면서 ReLU의 장점을 유지하기 위해 제안되었습니다.

Swish

소개 시기: 2017년
수학적 정의:
$f(x) = x \cdot \sigma(\beta x)$
- 여기서 $\sigma$ 는 시그모이드 함수이고, $\beta$ 는 학습 가능한 파라미터입니다.
등장 배경: 신경 아키텍처 검색을 통해 발견되었으며, 다양한 태스크에서 ReLU보다 우수한 성능을 보입니다.

GLU와 그 변형들의 발전 순서

1. GLU (Gated Linear Unit)

GLU는 2016년 Dauphin 등이 "Language Modeling with Gated Convolutional Networks" 논문에서 처음 소개한 활성화 함수입니다. GLU는 신경망의 학습 과정에서 입력 데이터의 중요도를 결정하는 게이팅(Gating) 메커니즘을 도입하여, 불필요한 정보는 차단하고 중요한 정보만을 다음 레이어로 전달하는 방식으로 작동합니다. 이는 모델의 성능 향상에 크게 기여할 수 있는 방법입니다.

링크 : https://arxiv.org/pdf/1612.08083

수학적으로 GLU는 다음과 같이 정의됩니다:

GLU(x, W, V, b, c) = (xW + b) \otimes \sigma(xV + c)

여기서:

x는 입력 벡터,
W, V는 가중치 행렬,
b, c는 편향 벡터,
$\sigma$ 는 시그모이드 함수로, 비선형 활성화 함수입니다.
- 활성화 함수(일반적으로 시그모이드 $\sigma$ )를 적용하여 출력할 정보의 양을 조절합니다.
$\otimes$ 는 요소별 곱셈을 의미합니다.

위 논문 Gated Convolutional Networks에서는 Gating 메커니즘을 통해 네트워크가 다음 단어를 예측하는 데 필요한 정보를 선택하도록 도와주며, 필요한 경우에만 정보를 전파합니다. 이러한 방식으로 네트워크는 어떤 단어 또는 특성이 다음 단어 예측에 중요한지를 선택할 수 있습니다.

Gating 메커니즘은 전통적인 비선형 활성화 함수(activation function) 대신에 사용할 수 있습니다.
- 예를 들어, Gated Linear Units(GLU)는 입력과 출력의 관계를 제어하는 게이트를 사용하여 정보 흐름을 더 잘 조절합니다. 이 방식을 사용하면 입력이 게이트와 결합되어 비선형성을 유지하면서도 정보가 보다 원활하게 전달될 수 있습니다.
GLU는 입력 데이터를 선형 변환한 후, 시그모이드 함수를 통해 게이트를 조절하여 결과를 선택적으로 통과시킵니다.
- 이 방식은 선형성과 비선형성을 결합하여 더 강력한 표현력을 제공하며, 딥러닝 모델의 학습 과정에서 중요한 정보만을 효과적으로 학습할 수 있게 도와줍니다.

2. Bilinear GLU

GLU와 함께 처음 논문에서 소개된 변형으로, Bilinear GLU는 시그모이드 함수를 제거하여 더 단순한 형태로 발전된 버전입니다.

링크 : https://arxiv.org/pdf/1612.08083

Bilinear GLU는 선형 변환만을 사용하며, 수학적으로 다음과 같이 정의됩니다:

Bilinear\ GLU(x, W_1, W_2, b_1, b_2) = (xW_1 + b_1) \otimes (xW_2 + b_2)

여기서 $\otimes$ 는 요소별 곱(element-wise product)을 의미합니다. Bilinear GLU는 두 개의 선형 변환을 결합하여 결과를 출력하는 방식으로 설계되어 있습니다. 이 방식에서 각각의 게이트를 상황에 맞게 조절하기 위해 시그모이드 함수를 사용하지 않습니다.

Bilinear GLU의 경우, 시그모이드가 없더라도 괜찮은 이유는, 비선형성을 Bilinear 방식으로 확보할 수 있기 때문입니다.
즉, Bilinear GLU는 두 입력 벡터 간의 상호작용(즉, bilinear transformation)을 통해 필요한 비선형성을 제공하며, 이를 통해 모델은 다양한 입력에 대한 복잡한 의존 관계를 모델링할 수 있기 때문이라고 합니다.

Bilinear GLU에서 비선형성을 확보하는 방식

다양한 선형 변환: Bilinear GLU에서는 입력 벡터 $X$ 를 두 개의 서로 다른 선형 변환을 통해 처리합니다. 각 변환이 서로 다른 가중치 행렬을 사용하여 $X$ 의 정보를 다르게 처리함으로써, 입력의 다양한 특성이나 패턴을 보다 자세하게 반영할 수 있습니다.

요소별 곱을 통한 상호작용: 두 선형 변환 결과를 요소별 곱으로 결합하면서, 각 요소 간의 상호작용을 정확하게 모델링할 수 있습니다. 이 조합은 단순한 선형 결합 이상의 의미를 가지며, 입력 데이터 간의 복잡한 관계를 포착하는 데 기여합니다.

차원 확장으로 인한 표현력 증가: 두 선형 변환과 요소별 곱이 결합됨으로써, 모델이 학습하는 정보의 공간이 확장되어 더 많은 표현력을 갖게 됩니다. 이는 모델이 입력 데이터의 다양한 특성을 포착하고, 더욱 복잡한 함수들을 근사할 수 있도록 도와줍니다.

결과적으로, Bilinear GLU는 차원을 확장하고 입력의 다양한 상호작용을 모델링함으로써 비선형성을 확보하고, 보다 복잡한 데이터 패턴을 학습할 수 있게 합니다. 이로 인해 모델의 성능이 향상될 수 있습니다.

3. ReGLU (ReLU-Gated Linear Unit)

ReGLU는 2020년 Shazeer의 "GLU Variants Improve Transformer" 논문에서 소개되었습니다. GLU의 시그모이드 함수를 ReLU로 대체한 변형입니다.

ReLU는 입력이 양수일 때는 그대로 통과시키고, 음수일 때는 0으로 만드는 간단한 비선형 활성화 함수입니다. (위 Activiation Function 참고)

수식으로 ReGLU는 다음과 같습니다:

ReGLU(x, W, V, b, c) = (xW + b) \otimes ReLU(xV + c)

ReLU는 계산이 간단하면서도 기울기 소실 문제를 잘 해결하는 장점이 있습니다. ReGLU는 이러한 ReLU의 장점을 이용하여 더 빠른 학습과 계산 효율성을 확보할 수 있었습니다.

4. GEGLU (GELU-Gated Linear Unit)

GEGLU 역시 Shazeer의 2020년 논문에서 소개된 변형입니다. GLU의 시그모이드 함수를 GELU(Gaussian Error Linear Unit)로 대체하였습니다.

GELU는 입력값을 Gaussian 분포 기반으로 처리하는 활성화 함수로, 더 자연스러운 비선형성을 제공합니다. (위 Activiation Function 참고)

GEGLU는 다음과 같이 정의됩니다:

GEGLU(x, W, V, b, c) = (xW + b) \otimes GELU(xV + c)

GELU는 특히 자연어 처리와 같은 복잡한 데이터에서 모델이 더 부드럽고 자연스럽게 학습할 수 있도록 도와줍니다. 이는 모델의 성능을 높이는 데 큰 역할을 했습니다.

5. SwiGLU (Swish-Gated Linear Unit)

SwiGLU는 Swish 함수를 활용한 GLU의 변형입니다. 이 또한 2020년 Shazeer의 논문에서 소개되었으며, 이후 2022년 Google의 "PaLM(Pathways Language Model)"에서 대규모 언어 모델에 적용되었습니다.

Swish 함수는 $Swish(x) = x \cdot \sigma(\beta x)$ 로 정의되며, 여기서 $\beta$ 는 학습 가능한 파라미터입니다. (위 Activiation Function 참고)

수학적으로 SwiGLU는 다음과 같습니다:

SwiGLU(x, W, V, b, c) = (xW + b) \otimes Swish(xV + c)

SwiGLU의 특징은 Swish 함수의 부드러운 기울기를 통해 학습 과정이 더욱 원활하고 안정적이라는 점입니다. 특히, PaLM과 같은 대규모 언어 모델에서 매우 좋은 성능을 발휘했으며, 이는 실제 대규모 데이터 학습에서도 유용함을 입증했습니다.

GLU와 그 변형들의 성능 비교 및 중요성

GLU와 그 변형들은 각기 다른 상황에서 더 나은 성능을 보일 수 있으며, 2020년 Shazeer의 논문에서는 이러한 변형들이 Transformer 구조에서 어떻게 성능을 개선하는지 비교하였습니다. 이 연구에서는 GEGLU와 SwiGLU가 다른 변형들보다 우수한 성능을 보였다고 보고되었습니다.

이러한 활성화 함수들은 각기 다른 상황에 맞춰 사용되며, 모델의 성능을 높이기 위한 다양한 실험과 개선을 거쳐 왔습니다. GLU의 게이팅 메커니즘은 데이터를 선별적으로 전달하여 학습 효율을 높이며, 이를 기반으로 한 변형들은 더 간단하거나 더 강력한 비선형성을 추가하여 모델의 표현력을 극대화하는 방향으로 발전해왔습니다.

정리

GLU에서 출발하여 Bilinear GLU, ReGLU, GEGLU, 그리고 SwiGLU까지 이어지는 발전 과정은 활성화 함수의 성능을 지속적으로 개선하기 위한 딥러닝 연구의 특성을 잘 보여줍니다. 각 변형은 이전 버전의 한계를 극복하거나 새로운 아이디어를 도입하여 모델의 성능을 향상시키는 데 초점을 맞추었습니다.

GLU: 선형성과 비선형성을 결합한 게이팅 메커니즘으로 시작.
Bilinear GLU: 더 단순한 계산을 위한 시그모이드 제거 버전.
ReGLU: 시그모이드 대신 ReLU를 사용하여 계산 효율성을 높임.
GEGLU: 더 부드러운 기울기를 제공하는 GELU 도입.
SwiGLU: Swish 함수를 이용해 대규모 모델에서 뛰어난 성능을 발휘.

이와 같은 활성화 함수들은 오늘날 딥러닝 모델, 특히 자연어 처리(NLP)와 같은 분야에서 중요한 도구로 자리 잡고 있으며, 데이터의 복잡한 패턴을 학습하고 모델의 성능을 높이는 데 핵심적인 역할을 하고 있습니다.