본 포스팅은 실제 데이터를 활용한 시계열 분석의 전반적인 프로세스 과정을 담고 있습니다. 분석 팁이나 피드백은 언제나 환영입니다!! 🙇‍♂️

분석의 순서는 아래와 같습니다. 해당 분석은 앞에서 다룬 시계열 개념을 기반으로 분석을 수행한 것이므로 개념을 찾아보고 싶다면 제 이전 포스트에서 확인하실 수 있습니다.

0. 참고
1. 데이터 선정 및 전처리
2. 데이터의 정상성(비정상) 프로세스 판별
3. 차분 수행 및 정상성(비정상) 프로세스 판별
4. ARIMA 모델 식별 및 추정 수행
5. 모델 평가

참고(라이브러리, 평가지표)

라이브러리

import os
import numpy as np
import pandas as pd

from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score

import statsmodels.api as sm
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.arima_model import ARIMA
from statsmodels.tsa.statespace.sarimax import SARIMAX 
from pmdarima.arima import auto_arima
import math

import itertools

import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
plt.style.use('seaborn-whitegrid')

평가지표

from sklearn import metrics

def mae(y_true, y_pred):
    return metrics.mean_absolute_error(y_true,y_pred) #MAE
def mse(y_true, y_pred):
    return metrics.mean_squared_error(y_true,y_pred) # MSE
def rmse(y_true, y_pred):    
    return np.sqrt(metrics.mean_squared_error(y_true,y_pred))  # RMSE
def r2(y_true, y_pred):    
    return metrics.r2_score(y_true,y_pred) # R2
def mape(y_true, y_pred):
    return np.mean(np.abs((y_pred - y_true) / y_true)) * 100 # MAPE

def get_score(model, y_true, y_pred):
    model = model
    mae_val = mae(y_true, y_pred)
    mse_val = mse(y_true, y_pred)
    rmse_val = rmse(y_true, y_pred)
    r2_val = r2(y_true, y_pred)
    mape_val = mape(y_true, y_pred)
    
    score_dict = {"model": model,
                  "mae" :  mae_val,
                  "mse" :  mse_val,
                  "rmse" : rmse_val,
                  "r2":    r2_val, 
                  "mape" : mape_val
                 }
    return score_dict

1. 데이터 선정 및 전처리

한국공항공사, https://www.airport.co.kr/www/extra/stats/timeSeriesStats/layOut.do?menuId=399

이번 분석에 사용된 데이터는 한국공항공사에서 제공하는 공항별 이용객 수 시계열 데이터로, 2002년 1월1일부터 2020년 9월1일까지 매월 수집된 총 여객기 사용 고객의 수입니다. 데이터를 확인해본 결과 여객기를 이용한 데이터이다 보니 최근 2020년 2월부터 심각해진 코로나 사태로 인하여 데이터가 심각하게 요동치는 것을 확인하였고, 외부 요인 없이 단순 ARIMA 모델로는 코로나라는 요인에 대한 정보를 학습하기 어려울 것 같아 분석 데이터의 기간을 조금 조정하여 코로나 사태가 터지기 이전인 2020년 1월까지의 데이터만을 사용하여 분석을 수행하도록 전처리를 수행해주었습니다.

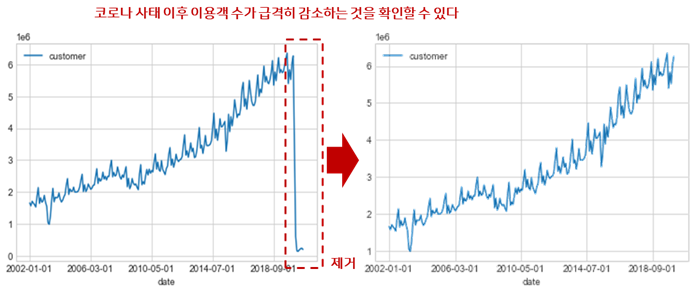
또한 모델 구축 후 예측에 대한 평가를 수행하기 위해 데이터를 Train, Test Split의 비율을 8:2로 두어 Train Dataset과 Test Dataset을 구축하였습니다.

2. 데이터의 정상성(비정상) 프로세스 판별

시각화를 통한 판단

먼저, 데이터에 아무런 변화를 주지 않고, 이를 파이썬 stats-models 모듈의 time series analysis에 내장되어 있는 seasonal decomposition 함수를 이용하여 데이터에서 추세(Trend), 계절(Seasonal), 예측오차(Residual)를 분리해 내어 시각화를 수행하였습니다. 위 그림의 좌측을 보면, 순서대로 본래 가지고 있는 데이터의 그래프, 추세 그래프, 계절 그래프, 예측오차 그래프를 의미합니다. 추세 그래프를 통해 데이터가 증가하고 있고, 계절 그래프를 통해 데이터가 주기를 가지고 있고, 예측오차 그래프를 통해 평균이 0이고 분산이 일정한 것을 확인할 수 있습니다. 이러한 그래프들을 통해 해당 데이터가 stationary하지 않다는 것을 시각적으로 확인할 수 있습니다.

decompostion = sm.tsa.seasonal_decompose(data['customer'],  model='additive')
fig = decompostion.plot()
fig.set_size_inches(10,10)
plt.show()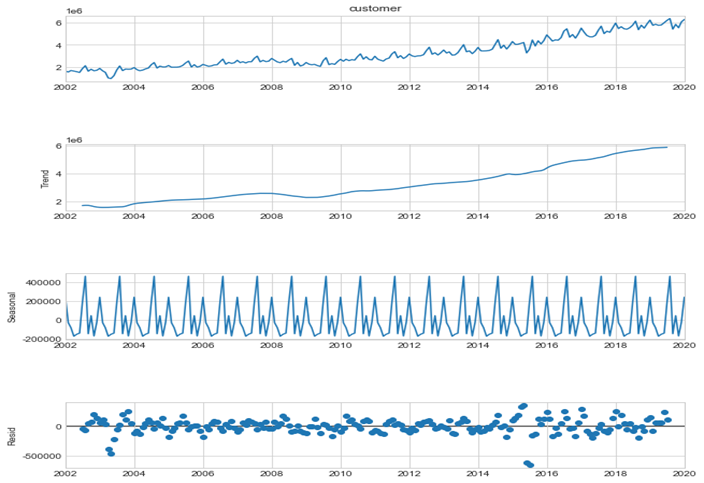

좀 더 자세한 분석을 위하여 해당 데이터를 가지고, ACF, PACF를 그려보았습니다. ACF와 PACF의 분포를 통해 stationary를 확인할 수 있습니다. 해당 데이터의 ACF positive autocorrelation을 가지며 서서히 감소하는 양상을 띄는 것으로 보아 non-stationary함을 추정할 수 있습니다.

fig, ax = plt.subplots(1,2,figsize=(10,5))
fig.suptitle('Raw Data')
sm.graphics.tsa.plot_acf(train_data.values.squeeze(), lags=30, ax=ax[0])
sm.graphics.tsa.plot_pacf(train_data.values.squeeze(), lags=30, ax=ax[1]);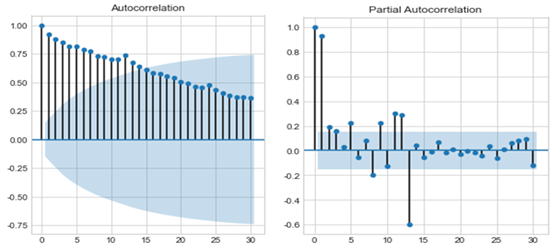

통계적 검정을 통한 판단

앞장에서는 데이터의 비정상성을 시각화를 통해 확인해보는 작업을 수행해보았습니다. 이번 단에서는 데이터의 비정상성을 통계적으로 검증해보기 위해 Durbin Watson Test와 Dickey Fuller Test를 수행해보았습니다.

Durbin Watson Test

Durbin-Watson Test를 사용하여 회귀 모형의 오차에 자기 상관이 있는지 검정할 수 있습니다. 자기 상관은 인접 관측치의 오차가 상관되어 있음을 의미합니다. Durbin-Watson Test의 귀무가설(H0)은 “the error terms are not autocorrelated”이고, 대립가설(H1)은 “the error terms are positively autocorrelated”입니다. 해당 데이터를 가지고 Durbin-Watson Test 를 수행한 결과 ρ는 1.10697로 0보다 크므로 귀무가설을 기각하게 됩니다. 이를 통해 해당 데이터는 autocorrelation을 가지고 있다고 할 수 있습니다.

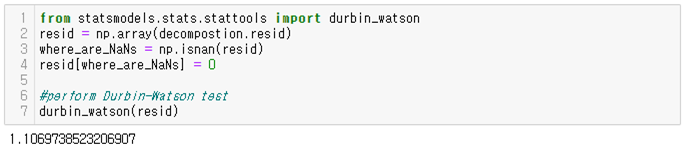
Dickey Fuller Test

Dickey Fuller Test를 사용하여 시계열 데이터가 정상성을 가지는지 가지지 않는지를 확인할 때 사용할 수 있습니다. Dickey Fuller Test 의 귀무가설(H0)은 “해당 데이터는 정상성을 가지지 않는다”이고, 대립가설(H1)은 “해당 데이터는 정상성을 갖는다”입니다. Dickey Fuller Test 를 수행해보면 p-value가 0.9884로 아주 높게 나타납니다. 그렇기 때문에 귀무가설을 기각하지 못했으므로 데이터는 정상성을 갖는다고 할 수 없습니다.

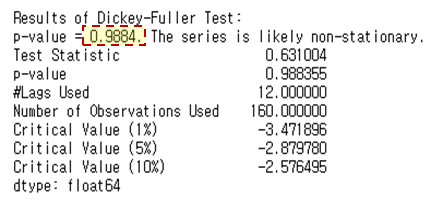
3. 차분 수행 및 정상/비정상 판별

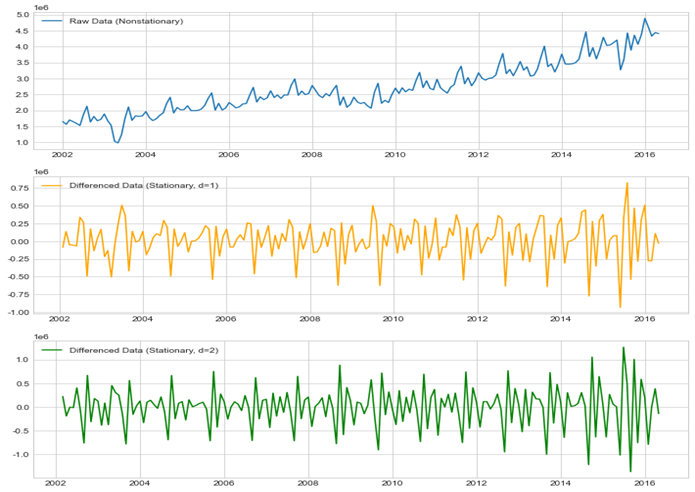
AR, MA, ARMA 모델을 적용하기 위해서는 데이터가 stationary해야 합니다. 앞에서 봤듯이 오리지널 데이터의 경우 데이터가 stationary하지 않기에 차분(differencing) 작업이 필요합니다. 본 분석에서는 1차 차분(d=1)과 2차 차분(d=2)을 수행하여 위 그래프로 나타냈습니다. 차분 작업을 통해 기존에 non-stationary하던 데이터가 stationary하게 된 것을 확인할 수 있었습니다. 각각 1차 차분, 2차 차분에 대하여 Dickey Fuller Test를 수행한 결과는 다음과 같습니다. 둘 다 p-value값이 0.05보다 작으므로 귀무가설을 기각하여 차분된 데이터는 stationary한 것을 확인할 수 있습니다.

1차 차분

diff_train_data = diff_train_data['customer'].diff()
print(diff_train_data.head())
diff_train_data = diff_train_data.dropna() #결측치 제거 코드(마지막 부분 제거)
print(diff_train_data.head())

2차 차분

diff2_train_data = diff_train_data.copy()
diff2_train_data = diff_train_data.diff()
print(diff2_train_data.head())
diff2_train_data = diff2_train_data.dropna() #결측치 제거 코드(마지막 부분 제거)
print(diff2_train_data.head())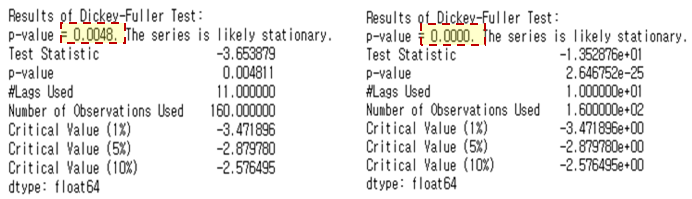

4. ARIMA 모델 식별 및 추정 수행

ARIMA는 ① 데이터 전처리 → ② 시범적으로 확인해볼 모델 구축 → ③ 파라미터의 추정(탐색) → ④ 타당성 확인 → ⑤ 최종모델선정의 흐름으로 분석이 진행됩니다. 앞에서 1차 차분, 2차 차분 둘 다 p-value가 0.05보다 작아 귀무가설을 기각하므로, 1차 차분한 데이터를 이용하여 분석을 수행해보았습니다. 일단 현재까지 ①단계인 데이터 전처리는 완료되었고, ②단계인 시범적으로 확인해볼 모델 구축하기 위해 1차 차분된 데이터를 이용하여 ACF와 PACF를 시각화하였습니다.

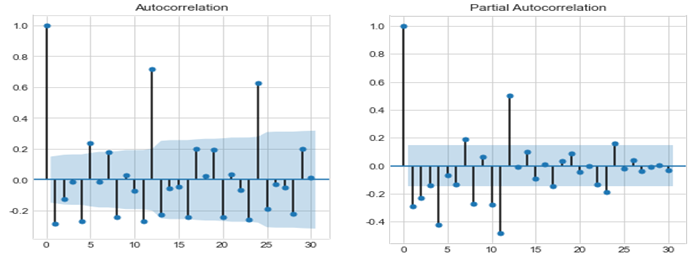
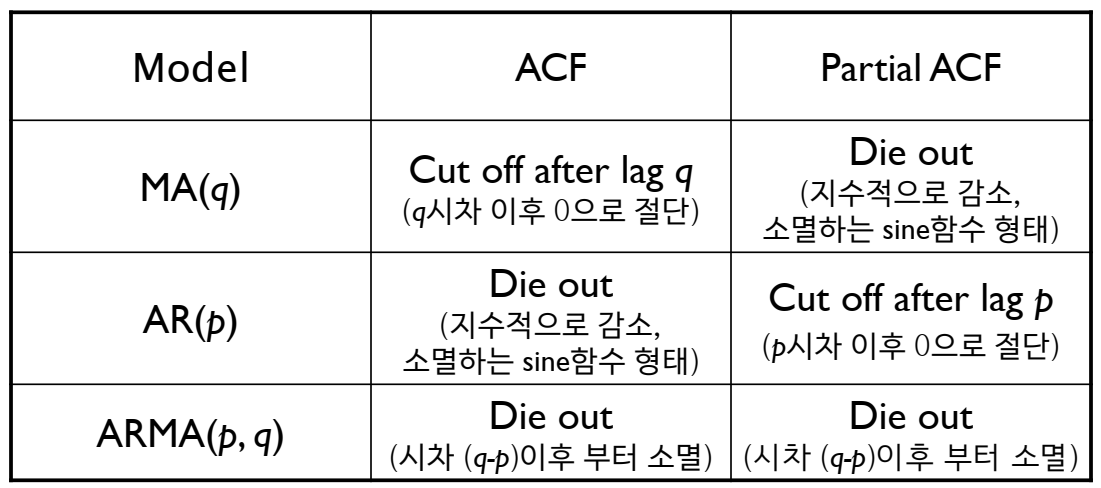
이를 확인해본 결과 ACF와 PACF가 지수적으로 감소하는 것을 확인할 수 있었고, cut off의 경우는 명확하게 나오지 않는 것을 확인할 수 없었습니다. 이에 아래 표를 참고하여 적용하여 (p,d,q)를 (0,1,1)로 하는 ARIMA모델을 시범적으로 구축해보았습니다.

(p,d,q)를 (0,1,1)로 하는 시범 ARIMA모델의 값은 다음과 같습니다. 구축된 모델은 AIC로 4767.825를 갖고, 각각의 constraint와 변수의 p-value는 0.05보다 작아 통계적으로 유의미한 값을 가지고 있습니다.

# ARIMA model fitting
# p =1 , 차분 = 1, moving average = 0

model = ARIMA(train_data.values, order=(0,1,1))
model_fit = model.fit()
model_fit.summary()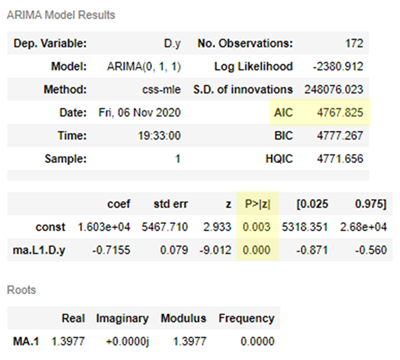

본격적으로 가장 적합한 parameter search를 위해 각각 d는 1로 고정(1차 차분)하고, p, q에 대하여 grid search를 수행하였습니다. (p,q)는 각각 0에서 5까지의 6개의 숫자 조합으로 총 36가지 조합으로 최적의 값을 다음과 같이 탐색해보았습니다. (ARIMA 출력물을 일부 생략)

# Parameter search 
auto_arima_model = auto_arima(train_data, 
                              start_p=0, max_p=5, 
                              start_q=0, max_q=5, 
                              seasonal=False,
                              d=1,
                              trace=True,
                              error_action='ignore',  
                              suppress_warnings=True, 
                              stepwise=False)

최적의 값을 다음과 같이 탐색해본 결과, p = 4, d =1, q = 0 일 때 AIC가 가장 작게 나오는 것을 확인할 수 있었습니다. (4,1,0)으로 구축된 모델의 AIC는 4749.253로, 이전 단계에서 시범적으로 만들어진 모델보다 작은 AIC값을 갖습니다. 각각의 constraint와 변수들의 p-value는 0.05보다 작아 통계적으로 유의미한 값을 가지고 있는 것을 확인할 수 있습니다.

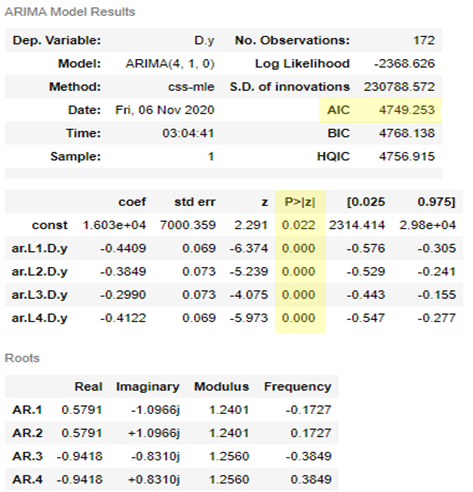
5. 모델 평가

앞에서 데이터 전처리 파트에서 언급했지만, 해당 데이터를 8:2 비율로 train과 test로 나누어 train 데이터는 모델 학습 및 hyper parameter tuning에 사용을 하였고, 나머지 test data는 예측 후 모델 성능을 평가하기 위해 남겨두었습니다. 다음은 지금 구축한 모델에 대한 test 기간에 대한 예측을 수행하고 이에 대한 평가해 보았습니다.

from pandas import Timestamp
%matplotlib inline

# set index
true_index = list(data.index)
predict_index = list(test_data.index)

# make array of true value
true_value = np.array(list(data['customer']))

# plot
fig, ax = plt.subplots(figsize=(12, 6))
ax.plot(true_index, true_value, label = 'True')
ax.plot(predict_index, pred, label = 'Prediction')
ax.vlines(Timestamp('2017-01-01 00:00:00'), 0, 100, linestyle='--', color='r', label='Start of Forecast');
ax.fill_between(predict_index, predicted_lb, predicted_ub, color = 'k', alpha = 0.1, label='0.95 Prediction Interval')
ax.legend(loc='upper left')
plt.show()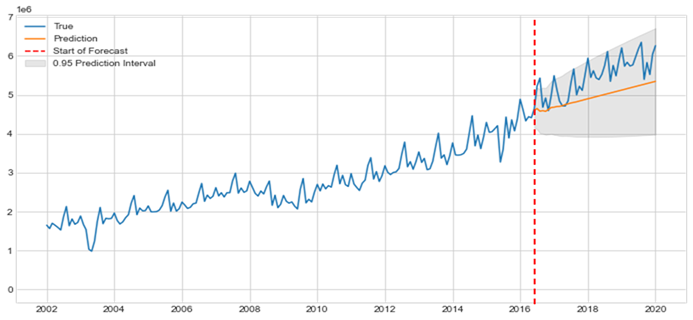

2002년 01월부터 2016년12월까지의 데이터로 학습한 ARIMA(4,1,0) 모델을 통해 2017년 1월부터 2020년 1월까지의 기간의 여객기 이용자수를 예측하고 위의 그래프를 그렸습니다. ARIMA 모델은 Trend를 잘 반영하여 예측을 하는 것을 확인할 수 있고, 계절성이 반영되지 않았게 때문에 seasonal cycle은 잘 예측해내지 못하는 것을 확인할 수 있습니다. 하지만 95% 신뢰구간안에 대부분의 예측 값들이 잘 들어오는 것을 확인할 수 있습니다. 이를 다음 performance metric들을 사용하여 모델 성능을 평가해보았습니다. 또한 이를 예측값과 실제값의 residual이 정규성을 띄고, autocorrelation이 없는 것을 확인할 수 있습니다.

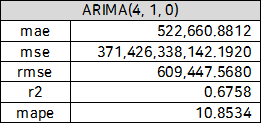
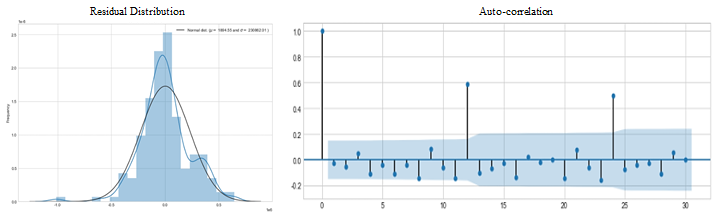
긴 글 읽어주셔서 감사합니다^~^