오늘은 알고리즘/자료구조를 공부하면서 평소 두려움에 떨며 제대로 공부하지 못했던 그래프에 대해 공부를 하며 정리해보았습니다. 공부하며 작성한 글이므로 반말이어도 양해부탁드립니다.

그래프

1. 그래프란?

• 그래프는 가장 일반화된 자료구조로, 연결된 객체들 사이의 관계를 잘 표현함.

그래프 이론

• 일반적으로 그래프와 관련된 다양한 문제를 연구하는 학문 분야를 그래프 이론이라고 함.
• 그래프는 수학자 오일러에 의해 처음 만들어졌으며, 모든 다리를 한번만 건너서 출발했던 장소로 돌아올 수 있는가?라는 문제가 답이 존재하지 않는다는 것을 그래프 이론을 통해 증명함.
• 일반적으로 그래프는 아래 두가지(정점, 간선)의 집합으로 구성됨
  • 표기 : $G = (V, E)$
  • 정점(Node) : 위치(객체) $V(G)$
  • 간선(Edge) : 위치(객체) 간의 관계 $E(G)$

그래프 종류

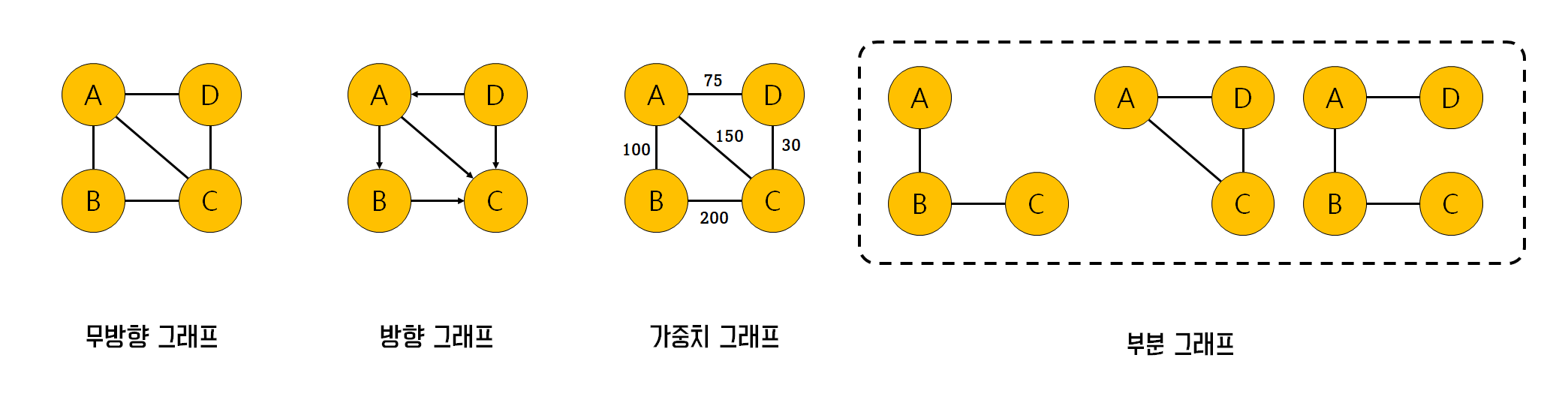
1. 무방향 그래프 (undirected graph)

   • 간선에 방향이 표시되지 않는 그래프

2. 방향 그래프 (directed graph)

   • 간선에 방향성이 존재하는 그래프

3. 가중치 그래프 (weighted graph)

   • 간선에 비용이나 가중치가 할당된 그래프

4. 부분 그래프 (subgraph)

   • 그래프를 구성하는 정점의 집합과 간선의 집합의 부분 집합으로 이루어진 그래프

그래프 용어 정리

1. 정점의 차수 (degree)
   • 정점에 연결된 간선의 수
2. 인접 정점 (adjacent vertex)
   • 간선에 의해 직접 연결된 정점
3. 경로 (path)
   • 간선을 따라 갈 수 있는 길, 한 정점에서 시작해서 다른 한 정점으로 이동하는 경로
4. 단순 경로 (simple path)
   • 경로 중에 반복되는 간선이 없는 경로
5. 싸이클 (cycle)
   • 단순 경로의 시작 정점과 종료 정점이 동일하여 해당 정점으로 다시 돌아오는 경로
6. 트리 (tree)
   • 사이클을 가지지 않는 연결 그래프
7. 연결 그래프 (connected graph)
   • 모든 정점들 사이에 경로가 존재하는 그래프
8. 완전 그래프 (complete graph)
   • 모든 정점간에 간선이 존재하는 그래프

2. 그래프의 표현

인접행렬을 이용한 표현

• 그래프에서 정점들의 연결관계를 표현하는 가장 간단한 방법으로,인접행렬(Adjacency matrix)을 사용하여 표현함
• 인접 행렬은 아래와 같은 특징들이 존재한다.
  - 노드의 번호를 인덱스
  - 간선의 존재유무(또는 가중치)가 인덱스의 값
  - 간선이 없는 노드에 대한 정보도 유지를 해야하기 때문에 공간복잡도가 좋지 않음

인접리스트를 이용한 표현

• 그래프의 각 정점과 연결된 인접 정접들을 각각의 리스트로 표현할 수 있는데 이러한 리스트를 인접리스트(Adjacency list)라고 함
• 각 정점은 인접 리스트를 이용해 자신과 간선으로 연결된 인접 정점들을 관리함
• 인접 리스트는 아래와 같은 특징들이 존재한다.
  - 파이썬에서는 딕셔너리를 주로 이용함
  - 연결된 정점에 대한 정보만 가지고 있기 때문에, 공간복잡도가 인접 행렬에 비해서 좋음
  - 가중치 정보는 반영이 되지 않음

3. 그래프의 탐색

• 그래프 탐색은 가장 기본적인 연산으로 하나의 정점에서 시작하여 모든 정점들을 한번씩 방문하는 작업을 의미함
• 실제로 많은 그래프 문제들이 단순히 정점들을 탐색하는 것만으로 해결됨
  - Ex) 미로 찾기 등
• 기본적인 탐색 알고리즘에는 깊이 우선 탐색 과 너비 우선 탐색의 두가지가 존재함

🎁 여기서 잠깐!
파이썬은 collections라는 모듈에서 defaultdict, Counter, deque 등의 기능을 제공하는데, 이중 deque와 defaultdict를 사용하면 유용하게 각각 BFS와 DFS를 정의할 수 있다!

• deque : 양쪽 끝에서 빠르게 추가와 삭제를 할 수 있는 리스트류 컨테이너
• Counter : 해시 가능한 객체를 세는 데 사용하는 딕셔너리 서브 클래스
• OrderedDict : 항목이 추가된 순서를 기억하는 딕셔너리 서브 클래스
• defaultdict : 누락된 값을 제공하기 위해 팩토리 함수를 호출하는 딕셔너리 서브 클래스

from collections import deque
from collections import defaultdict

# defaultdict를 이용하는 경우
a = defaultdict(list) # list형식으로 저장해주겠다는 뜻

# 큐를 이용하는 경우
q = deque()

깊이 우선 탐색 (DFS)

• 깊이 우선 탐색 (depth first search, DFS)은 스택 또는 재귀을 이용한 미로 탐색과 유사함
• 미로를 탐색할 때 한 방향으로 갈 수 있는 데까지 계속 진행하다가, 더 이상 진행이 불가능하면 다시 가까운 갈림길로 돌아와 다른 방향으로 다시 탐색하는 방법
• DFS 과정 (출처 : https://gmlwjd9405.github.io/2018/08/14/algorithm-dfs.html)
  

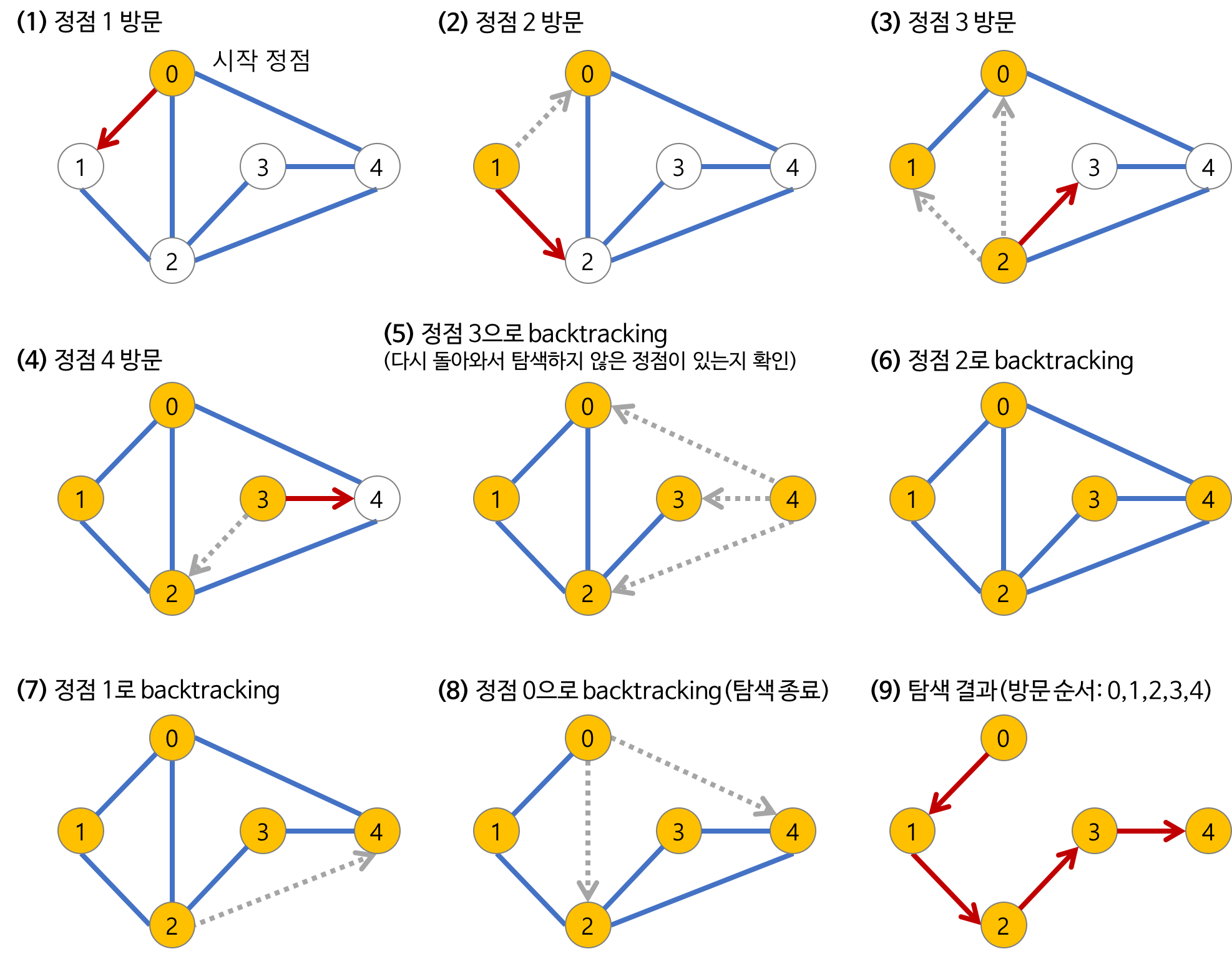
참고

• v : 시작 노드
• n : 노드(node)의 개수
• m : 간선(edge)의 개수
• arr : 인접행렬
• a : 인접리스트

인접행렬과 재귀를 이용한 DFS

# 이전 방문 여부 확인
check = [False] * (n+1)

# DFS 함수 정의
def dfs(v):
  check[v] = True # v노드를 방문함

  # 방문 가능한 모든 노드를 전부 순회
  for i in range(1, n+1):
    # i 조건 : v와 인접해야함 + 이전에 방문한 적이 없어야 함
    if arr[v][i] == 1 and check[i] == False:
      dfs(i)

# 함수 실행
dfs(v)

인접리스트와 재귀를 이용한 DFS

# 이전에 방문한적이 있었는지 체크
check = [False] * (n+1)

# DFS 함수 정의
def dfs(v):
  check[v] = True # v노드를 방문함

  # 방문 가능한 모든 노드를 전부 순회
  for i in a[v]:
    # 인접 리스트는 인접한 정점에 대한 정보만 들어있다.
    # 따라서, 이전에 방문한 적이 있었는지만 확인하면 된다.
    if check[i] == False:
      dfs(i)

# 함수 실행
dfs(v)

인접행렬과 스택을 이용한 DFS

# 이전 방문 여부 확인
check = [False] * (n+1)

stack = deque()  

def dfs(start):
  check[start] = True
  stack.append(start)
  
  # 스택이 비어있으면 종료
  while stack:
    v = stack.pop()
    print(v)
    for i in range(n, -1, -1):
      if arr[v][i] == 1 and check[i] == False:
        check[i] = True
        stack.append(i)

dfs(v)

인접리스트와 스택을 이용한 DFS

# 이전에 방문한적이 있었는지 체크
check = [False] * (n+1)

stack = deque()  

def dfs(start):
  check[start] = True
  stack.append(start)
  
  # 스택이 비어있으면 종료
  while stack:
    v = stack.pop()
    print(v)
    for i in a[v]:
      if check[i] == False:
        check[i] = True
        stack.append(i)

dfs(v)

---

너비 우선 탐색 (BFS)

• 너비 우선 탐색 (breadth first search, BFS)은 시작 정점으로부터 가까운 정점을 먼저 방문하고, 멀리 떨어져 있는 정점에는 나중에 방문하는 순회 방법
• 너비 운선 탐색을 위해서는 가까운 거리에 있는 정점들을 차례로 저장하고, 들어간 순서대로 꺼내는 방식으로 진행되는 데 이를 위해 큐(Queue)를 사용함.
• 큐를 이용해서 현재 노드에서 갈 수 있는 모든 노드를 큐에 넣는 방식 (큐에 들어가면, 방문한 것으로 간주함)
• 다시말해, 정점들이 방문될 때마다 큐에 인접 정점을 삽입하고, 더 이상 방문할 인접 정점이 없는 경우 큐의 맨 앞의 정점을 꺼내 그 정점과 인접한 정점들을 차례대로 방문함
• BFS 과정 (출처 : https://gmlwjd9405.github.io/2018/08/15/algorithm-bfs.html)
  

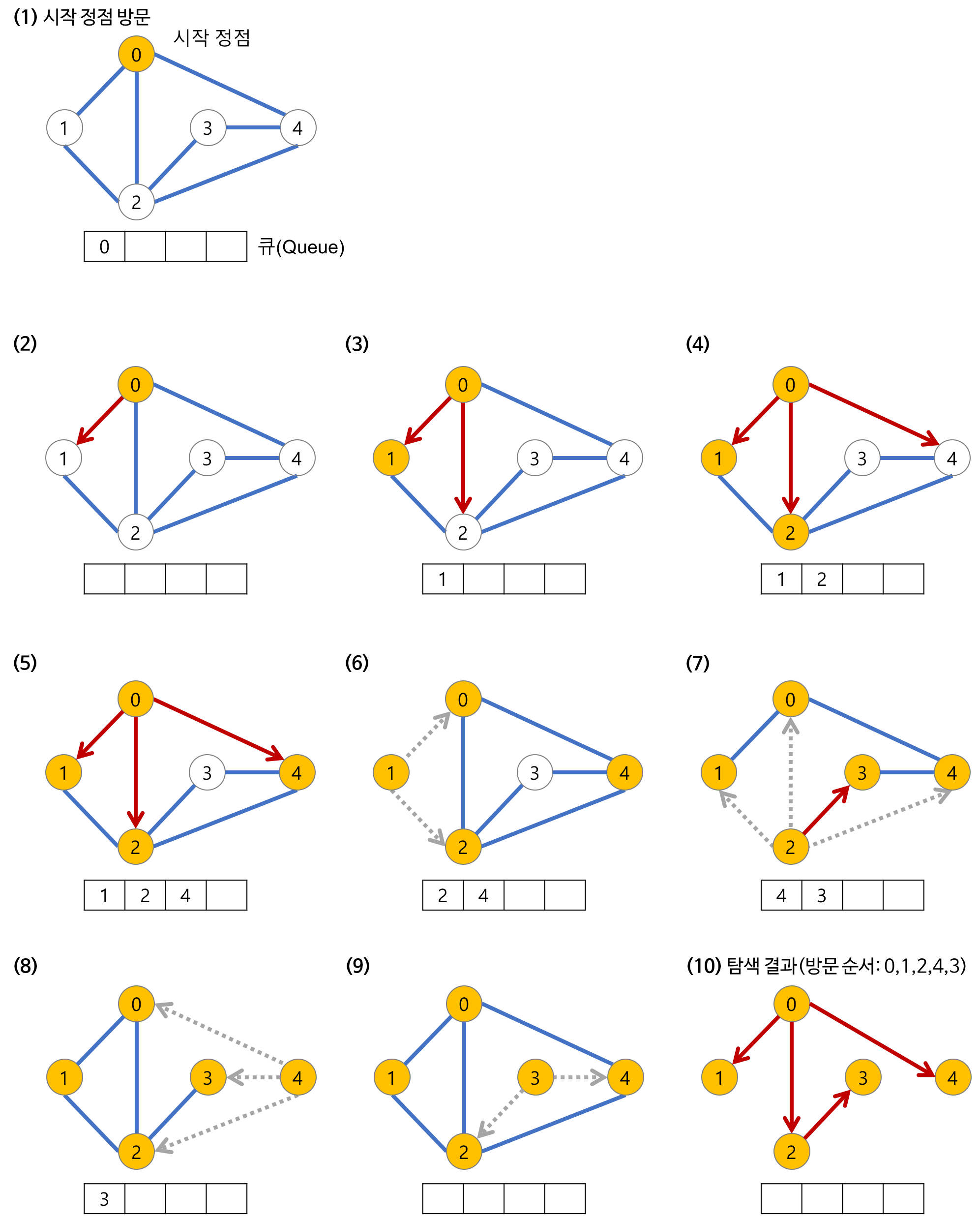
참고

• start : 시작 노드
• n : 노드(node)의 개수
• m : 간선(edge)의 개수
• arr : 인접행렬
• a : 인접리스트

인접행렬과 큐를 이용한 BFS

# 이전에 방문한적이 있었는지 체크
check = [False] * (n+1)

# 큐 선언
q = deque()

# BFS정의
def bfs(v):
  # 방문 체크
  check[v] = True
  # 큐에 추가
  q.append(v)
  
  # 큐에 더 이상 방문할 노드가 없으면 종료
  while q:
    # FIFO
    pop = q.popleft()
    # 방문 가능한 모든 노드를 전부 순회
    for i in range(1, n+1):
      # i 조건 : pop과 인접해야함 + 이전에 방문한 적이 없어야 함
      if arr[pop][i] == 1 and check[i] == False:
        check[i] = True
        q.append(i)

# 함수 실행
bfs(v)

인접리스트와 큐를 이용한 BFS

# 이전에 방문한적이 있었는지 체크
check = [False] * (n+1)

# 큐 선언
q = deque()

# BFS정의
def bfs(v):
  # 방문 체크
  check[v] = True
  # 큐에 추가
  q.append(v)
  
  # 큐에 더 이상 방문할 노드가 없으면 종료
  while q:
    # FIFO
    pop = q.popleft()
    # 인접 리스트는 인접한 정점에 대한 정보만 들어있다.
    # 따라서, 이전에 방문한 적이 있었는지만 확인하면 된다.
	for i in a[v]:
      if check[i] == False:
        check[i] = True
        q.append(i)

# 함수 실행
bfs(v)

긴 글 읽어주셔서 감사합니다 ^~^