본 포스트는 고려대학교 강필성 교수님의 강의를 수강 후 정리를 한 것입니다. 작성 및 설명의 편의를 위해 아래는 편하게 작성한 점 양해부탁드립니다.

Dimensionality Reduction

Supervised Variable Extraction

차원축소는, 모델링을 하기 위해 내가 가진 데이터의 정보를 최대한 보존하면서, 훨씬 더 compact하게 데이터셋을 구성하는 것을 목적으로 하며, 크게 변수선택(Variable Selection, 변수들의 부분 집합 선택)과 변수추출(Variable Extraction, 변수들을 요약하는 새로운 변수 생성)이 있다.

이전 포스트에서는 아래 표에서 Supervised Variable Selection을 살펴보았다. 오늘은 Supervised Variable Extraction에 대해 이야기를 풀어보도록 하겠다.

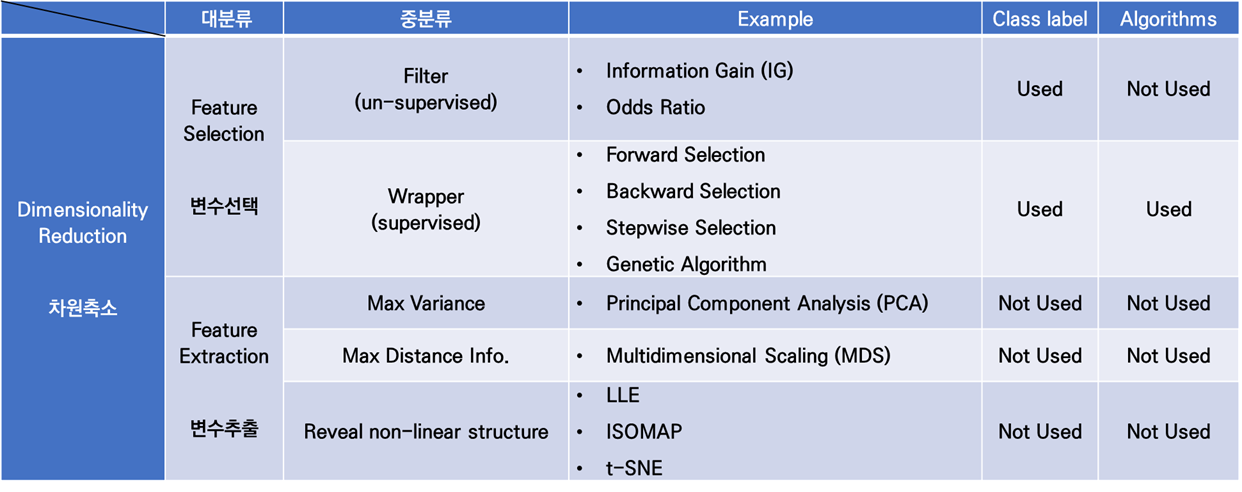
MDS란

Multi-Dimensional Scaling(MDS), 다차원척도법이란, D-차원 공간 상의 객체들이 있을 때 그 객체들의 거리(between object distance)가 저-차원 공간 상에도 최대한 많이 보존되도록 하는 좌표계를 찾는 것을 의미한다.

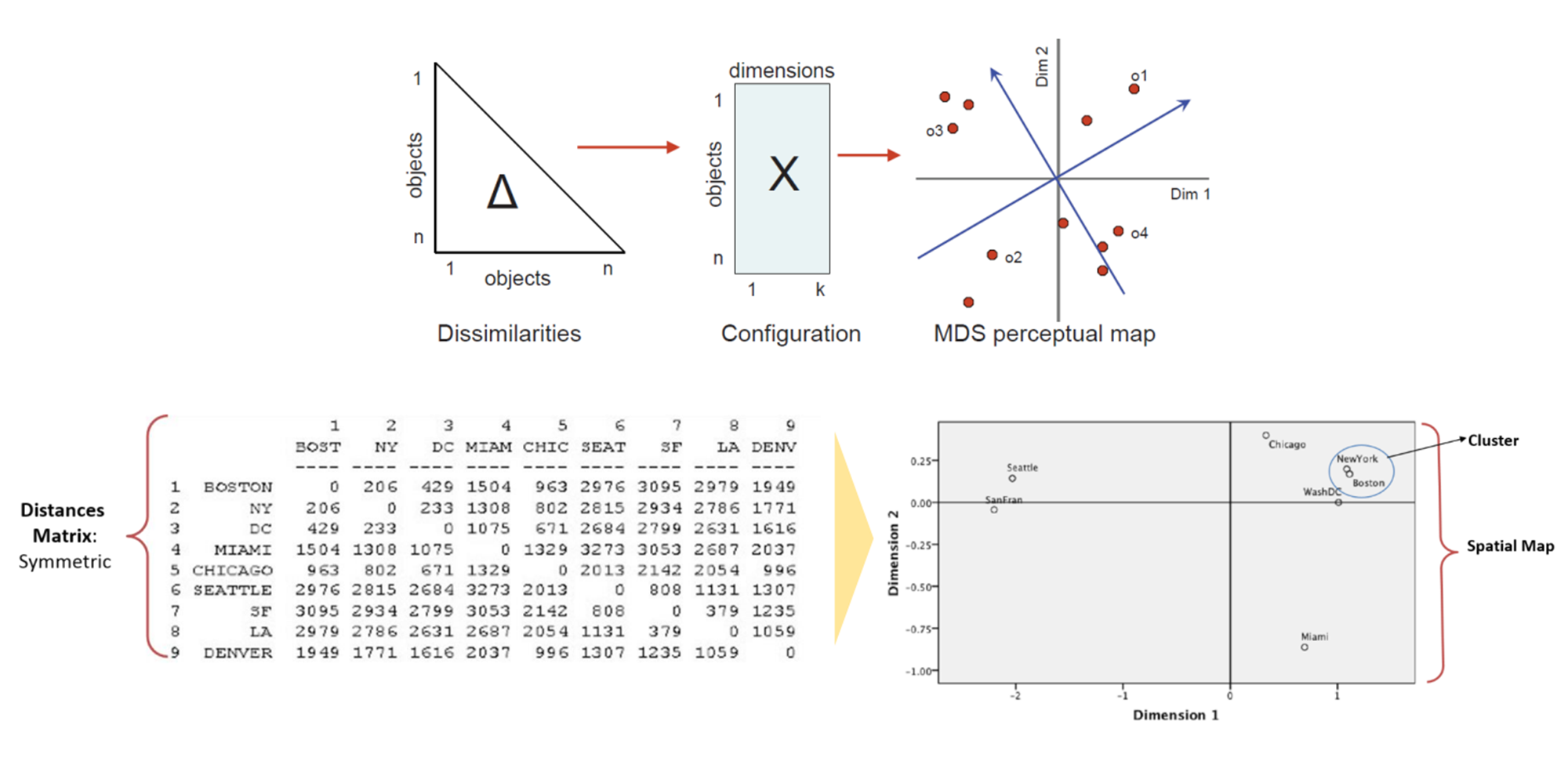
Distance matrix를 통해서 저-차원 상의 각각의 객체들이 갖는 좌표 시스템을 찾는 것이 목적

지난번에 다루었던 PCA(링크)와 MDS를 비교하면 다음과 같이 표로 정리할 수 있다.

추가적으로 PCA를 적용할 수 있는 모든 데이터는 거리에 대한 값으로 표기 및 MDS 적용이 가능하지만, 역은 성립하지 않는다.

MDS 프로세스

[1] Construct Proximity/Distance Matrix 단계

• 근접/거리 행렬(D, distance matrix) 구축 단계이다.
• 거리-행렬이 가져야할 특징은 아래와 같다:
  1. $d_{ij}≥0$
  2. $d_{ii}=0$
  3. $d_{ij}= d_{ji}$
  4. $d_{ij}≤d_{ik}+d_{jk}$ (∵ 삼각부등식)
• Distance Measure: Euclidean, Manhattan, etc.
• Similarity Measure: Correlation, Jaccard, etc.
• (참고) MDS의 최종목적
  - 아래 $d_{rs}$ 식을 바탕으로 $x_{r}$, $x_{s}$를 찾아내는 것

$d_{rs}^2=(x_r-x_s )^T (x_r-x_s)$

[2] Extract the coordinates that preserve the distance information 단계

• 거리 정보를 보존하는 좌표 시스템을 찾는 단계이다.
• D라는 distance matrix에서 한 번에 x를 구하기 어려우므로, B라는 매개체인 내적 Matrix를 도출하고 그 다음에 X를 구한다.

$D_{(n×n)} → B_{(n×n)} → X_{(d×n)} ⇔ D ≔ (X_r-X_s )^T (X_r-X_s ) → B ≔ X_r^T X_s → X ≔ X$

• B는 다음과 같이 정의된며 몇 가지 가정을 따른다.

$[B]_rs=b_rs=X_r^T X_s$

• 가정
  1. $∑_{r=1}^{n}x_{ri}=0 (i=1,2,…,p)$, 모든 변수의 합은 0이다.
  2. $d_{rs}^{2}=(X_r-X_s )^T (X_r-X_s )=X_r^T X_r+X_s^T X_S-2X_r^T X_s$

• r에 대한 합 (1):
  

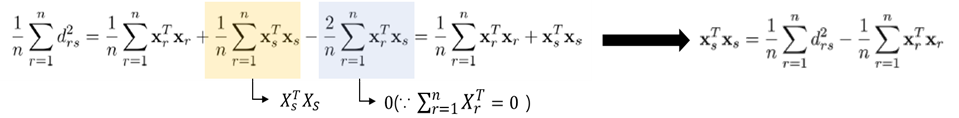
• s에 대한 합 (2):
  

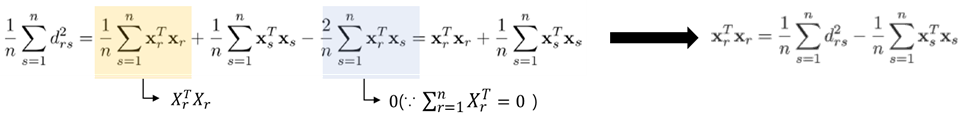
• r과 s에 대한 합 (3):
  

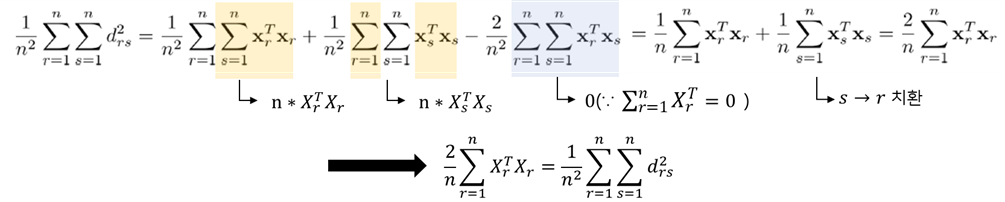
• B(inner product matrix)를 구해보자
  

• 좌표시스템 X를 구해보자. B는 이미 앞에서 언급했듯이 다음과 같이 정의될 수 있다.

$B_{(n×n)}=XX^T$

$rank(B)=rank(XX^T )=rank(X)=p$

($X_{(n×p)}$, rank는 선형독립인 열들의 최대의 개수를 의미하며, p<n조건을 만족한다.)

• 이때 행렬 B는 inner product matrix 이기 때문에 다음과 같은 성질을 만족하고, 0인 eigenvalue값들을 제거하면 다음과 같이 표현할 수 있다.

• $B = XX^T$이므로, $X = V_{1} Λ_{1}^{1/2}$임을 구할 수 있다.

긴 글 읽어주셔서 감사합니다 ^~^