(설명추가) Q-Learning: 강화학습의 핵심 개념과 이해

혁펜하임님의『Easy! 딥러닝』책을 보다보면 엄청 중요한 내용들이 쉽게 풀이되어 있습니다. 처음 배우시는 분들도 쉽게 따라오실 수 있습니다.

• 아래 그림과 같이 쉬운 예제와 용어 설명이 되어 있습니다.

사진 출처 : 책 내용 일부 사진 직접 촬영

강화학습에 문외한이었던 저도 개념에 대해서 쉽게 맥락을 잡을 수 있어서 개인적으로 너무 유익한 시간이었습니다. (pg 29 - 37)

하지만! 저는 여기서 그치면 아쉽기 때문에 좀 더 깊게 삽질(?) 좀 더 해보겠습니다 ㅎㅎ

이미지 출처: 이말년 시리즈 (직접 편집)

이번 포스팅에서는 강화학습 내용을 정리해보고, Q-learning에 대해서 보다 더 상세하게 공부해보도록 하겠습니다.

1. 강화학습과 Q-Learning의 기본 개념

강화학습(Reinforcement Learning, RL)은 인공지능(AI) 에이전트가 환경과 상호작용하면서 최적의 행동을 학습하는 알고리즘입니다.

이미지 출처: https://minsuksung-ai.tistory.com/13

그중에서도 Q-Learning은 환경의 동작 방식(전이 확률이나 보상 함수 등)을 미리 알지 않아도 학습할 수 있는 대표적인 알고리즘입니다.

• 즉, 환경을 직접 탐색하며 최적의 행동을 학습하는 방식으로 동작합니다.
• 특정 상태에서 특정 행동을 했을 때 얻을 수 있는 보상을 경험을 통해 예측하고, 이를 활용하여 점진적으로 더 나은 정책을 만들어 나갑니다.

강화학습이란?

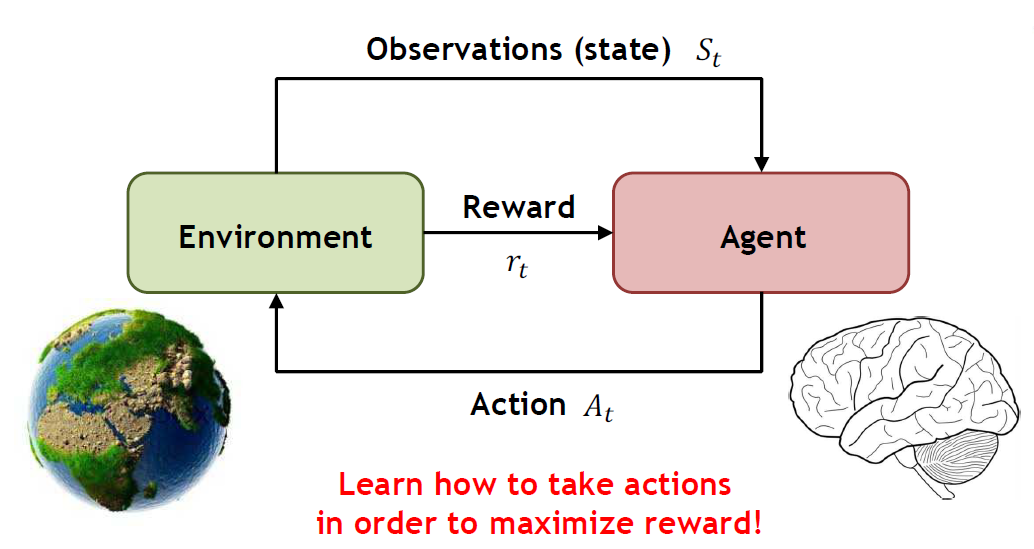
강화학습은 보상을 최대화하는 행동을 학습하는 과정입니다.

• 에이전트(agent)는 환경(environment)과 상호작용하면서 상태(state)를 관찰하고, 가능한 행동(action) 중 하나를 선택하여 보상을 받습니다.

위와 같은 과정을 반복하면서 최적의 정책(policy)을 학습하게 됩니다.
(보다 쉬운 이해를 위해서는 책을 참고해주세요 )

이미지 출처 : R로 쉽게 배우는 강화학습

강화학습의 핵심 개념은 다음과 같습니다.

1. State (상태, $S$): 환경에서 에이전트가 현재 위치한 상태입니다.
2. Action (행동, $A$): 특정 상태에서 수행할 수 있는 선택지입니다.
3. Reward (보상, $R$): 특정 행동을 수행했을 때 환경으로부터 받는 보상입니다.
4. Episode (에피소드): 시작 상태에서 목표 상태까지 도달하는 일련의 단계입니다.
5. Policy (정책, $\pi$): 상태에서 행동을 선택하는 전략을 의미합니다.
6. State-Action Value Function (행동 가치 함수, $Q(S,A)$): 특정 상태에서 특정 행동을 수행했을 때 기대되는 장기적인 보상을 나타냅니다.

Q-Learning은 책에서 소개하는 핵심 강화학습 기법 중 하나로, Q-Table이라는 구조를 사용하여 각 상태에서의 행동 가치를 학습합니다.
(For more. Q-Table은 "6. Q-Table이란?"을 참고해주세요)

---

2. 행동 가치 함수(Q-Value Function)란?

Q-Learning의 핵심은 행동 가치 함수(Q-Value Function)를 학습하는 것입니다.

• 행동 가치 함수 $Q(S, A)$는 특정 상태 $S$ ($State$)에서 특정 행동 $A$ ($Action$)를 선택했을 때 기대되는 누적 보상을 나타냅니다.

Q-Learning에서는 Q-Table이라는 형태로 각 상태와 행동에 대한 가치를, Q-값으로 저장하며, 학습을 통해 이 값을 지속적으로 업데이트합니다.

• Q-값을 반복적으로 업데이트함으로써 에이전트는 더 높은 보상을 기대할 수 있는 행동을 선택하는 경향을 가지게 되며, 최적의 정책을 형성하게 됩니다.

---

3. Q-Learning의 학습 과정

Q-Learning의 학습은 Q-Table을 반복적으로 업데이트하는 과정으로 진행됩니다.

학습 단계는 다음과 같습니다.

✔️ Step 1: Q-Table 초기화

• 모든 Q-값을 0으로 설정합니다.

✔️ Step 2: 행동 선택 (Exploration vs. Exploitation)

• 에이전트는 탐색(Exploration)과 활용(Exploitation)을 조합하여 행동을 선택합니다.

• $\epsilon$-탐욕($\epsilon$-greedy) 정책을 사용합니다.

✔️ Step 3: 보상 관찰 및 Q-값 업데이트

• Q-값은 아래 벨만 방정식(Bellman Equation)을 이용해 갱신됩니다.

  $Q(S, A) \leftarrow Q(S, A) + \alpha \Big[ R + \gamma \max_{a'} Q(S', a') - Q(S, A) \Big]$
  • $Q(S, A)$ : 현재 상태 $S$에서 행동 $A$를 했을 때의 Q-값
  • $\alpha$: 학습률 (Learning Rate, 0~1) → 업데이트 비율을 조절
  • $\gamma$: 할인율 (Discount Factor, 0~1)
  • $R$: 현재 행동을 수행한 후 받은 보상 (Reward)
  • $\max_{a'} Q(S', a')$: 다음 상태에서 최적 행동의 Q-값

이 과정을 충분히 반복하면 Q-값이 수렴하고, 최적 정책을 찾을 수 있습니다.

❓ (참고) 벨만 방정식 (Bellman Equation) 설명

• 벨만 방정식(Bellman Equation)은 최적 정책(Optimal Policy)을 찾기 위해 상태(State)와 행동(Action) 간의 관계를 수식화한 식입니다.
  • 이는 Q-Learning과 같은 강화학습에서 Q-값을 업데이트하는 핵심 원리로 작용합니다.
  • 벨만 방정식은 현재 상태에서의 최적 Q-값을 미래의 기대 보상(Discounted Future Reward)으로 표현한 재귀 방정식입니다.

---

4. ε-greedy 기법과 Exploration & Exploitation 전략

Q-Learning에서는 탐색(Exploration)과 활용(Exploitation)의 균형이 중요합니다.

• 탐색이 부족하면 최적 행동을 찾지 못할 가능성이 있고, 반대로 탐색이 과하면 최적 정책 수렴이 느려질 수 있습니다.

이를 해결하기 위해 $\epsilon$-greedy 전략이 사용됩니다.

• 탐색(Exploration):

  • 새로운 행동을 시도하여 더 나은 보상을 찾음.
  • 미지의 영역을 탐험하며, 새로운 전략을 발견할 가능성을 높임.

• 활용(Exploitation):

  • 현재까지 학습한 Q-값을 기반으로 최적의 행동을 선택함.
  • 지금까지의 경험을 바탕으로 가장 높은 보상을 주는 선택지를 취함.

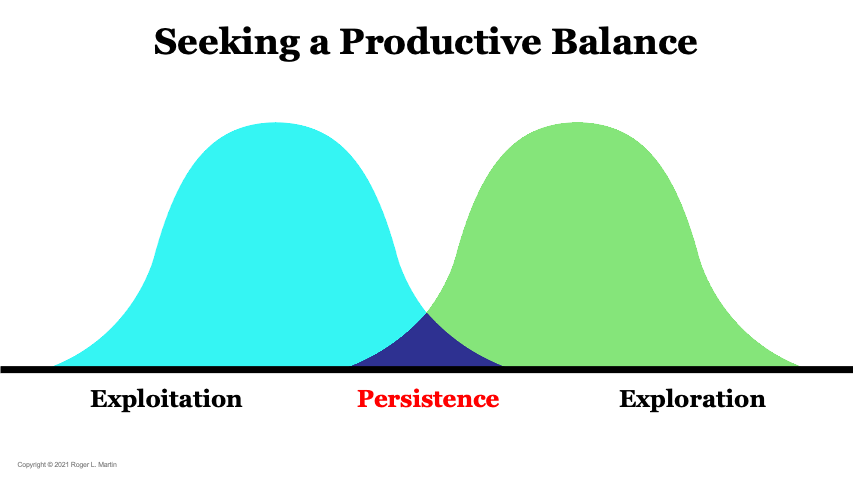
Image Source: https://rogermartin.medium.com/balancing-exploration-and-exploitation

ϵ-greedy 기법

$\epsilon$-greedy 기법은 특정 확률($\epsilon$)로 탐색을 수행하고, 나머지 확률($1-\epsilon$)에서는 현재 최적의 행동을 선택하도록 설계된 기법입니다.

• 초반에는 탐색을 더 많이 수행하도록 설정하고, 학습이 진행될수록 활용 비율을 점진적으로 증가시키는 방식이 일반적입니다.

(참고) ϵ-greedy 기법은 on-policy인가?
=> 결론부터 말하자면, NO!! ϵ-greedy 기법은 off-policy기법입니다.

• RL(강화학습)에서 말하는 Policy(정책, $\pi$)는 에이전트가 특정 상태($S$)에서 특정 행동($A$)을 선택하는 규칙입니다.
  • 즉, "현재 상태에서 어떤 행동을 해야 하는가?"를 결정하는 함수입니다.
• $\epsilon$-greedy는 특정한 방식으로 행동을 선택하는 방법론이지, 정책 자체를 학습하는 방식이 아닙니다.
  • 즉, "탐색을 얼마나 할 것인가?"를 조정하는 역할을 하는 것이지, 어떤 행동이 최적인지를 학습하는 것은 아닙니다.

비교 항목	On-Policy Learning	Off-Policy Learning
학습하는 정책과 실행하는 정책	동일함 (같은 정책을 학습)	다름 (최적 정책을 학습)
탐색과 활용의 관계	탐색과 활용이 함께 이루어짐	탐색을 통한 경험을 활용하여 최적 행동 학습
경험 재사용(Experience Replay)	사용 어려움	사용 가능 (데이터 재사용 가능)
예제 알고리즘	SARSA, PPO	Q-Learning, DQN

---

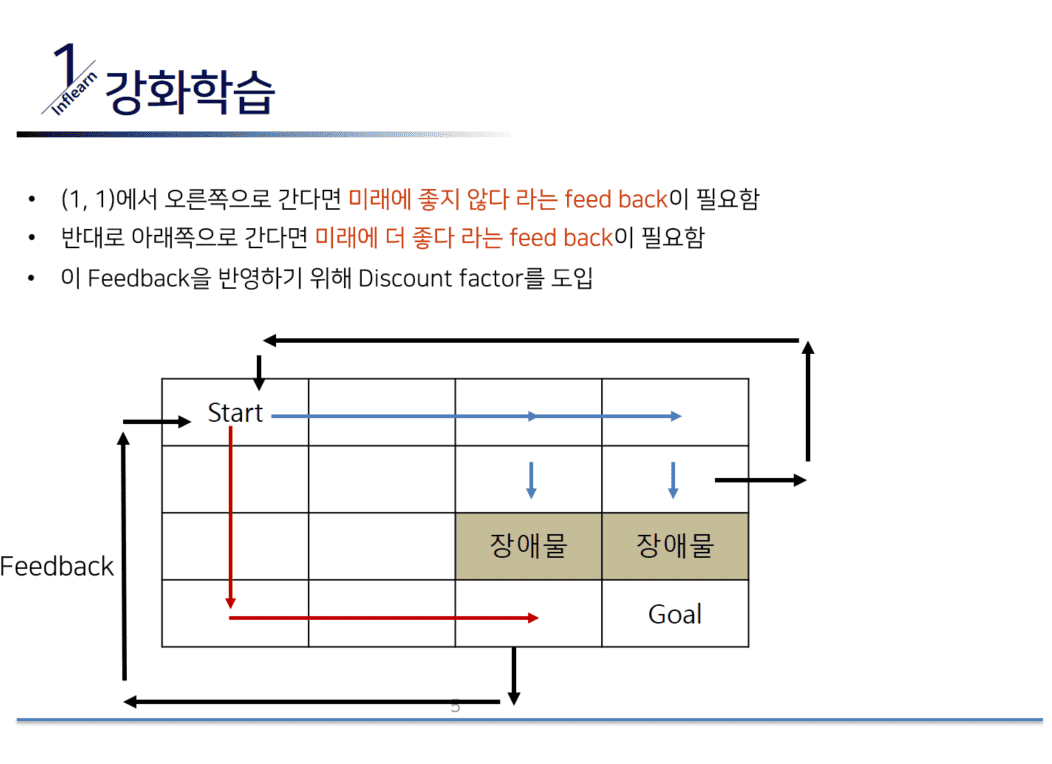
5. 할인율(Discount Factor)의 역할

Q-Learning에서는 미래 보상의 가치를 현재 보상과 비교할 때 할인율(Discount Factor, $\gamma$)을 적용합니다.

• 할인율이 높을수록 먼 미래의 보상까지 고려하는 반면, 낮을수록 가까운 보상을 더 중요하게 여깁니다.

  • $\gamma$ 값이 1에 가까울수록 → 장기적인 보상을 중시 (예: 마라톤 경기 전략 수립)
  • $\gamma$ 값이 0에 가까울수록 → 즉각적인 보상을 중시 (예: 당장 이득을 얻는 도박 전략)

일반적으로 $\gamma$는 0.9~0.99 사이로 설정됩니다.

• 높은 할인율은 장기적인 목표를 고려하며, 낮은 할인율은 즉각적인 결과에 집중하게 합니다.

이 설정은 문제의 특성과 목표에 따라 달라질 수 있습니다.

6. Q-Table이란?

Q-Table은 각 상태(state)에서 가능한 행동(action)에 대한 예상 보상 값(Q-Value)을 저장하는 테이블입니다.

• Q-Learning 알고리즘에서는 이 테이블을 점진적으로 업데이트하면서 최적의 행동을 학습합니다.

Q-Table의 구조는 다음과 같습니다.

상태(State)	행동 1	행동 2	행동 3	행동 4
S1	0.5	0.2	-0.1	0.0
S2	0.0	0.8	0.3	-0.5
S3	-0.3	0.7	0.5	0.2

여기서 각 셀의 값(Q-Value)은 해당 상태에서 특정 행동을 수행했을 때 기대할 수 있는 보상을 의미합니다.

• 학습이 진행됨에 따라 Q-Table의 값이 점점 더 정확한 보상 예측값으로 수렴합니다.

---

7. Q-Learning의 구현 예제

(참고용) 아래는 간단한 Q-Learning 알고리즘을 구현하는 Python 코드입니다.

import numpy as np

# 환경 설정
n_states = 16  # 상태 수
n_actions = 4  # 행동 수 (상, 하, 좌, 우)
goal_state = 15  # 목표 상태

# Q-Table 초기화
Q_table = np.zeros((n_states, n_actions))

# 하이퍼파라미터 설정
learning_rate = 0.8
discount_factor = 0.95
exploration_prob = 0.2
epochs = 1000

# Q-Learning 알고리즘
for epoch in range(epochs):
    current_state = np.random.randint(0, n_states)  # 무작위 상태에서 시작
    
    while current_state != goal_state:
        # 행동 선택 (epsilon-greedy 전략)
        if np.random.rand() < exploration_prob:
            action = np.random.randint(0, n_actions)  # 탐색
        else:
            action = np.argmax(Q_table[current_state])  # 활용

        # 환경에서 다음 상태로 이동 (단순화된 이동)
        next_state = (current_state + 1) % n_states

        # 보상 정의 (목표 상태 도달 시 보상 부여)
        reward = 1 if next_state == goal_state else 0

        # Q-값 업데이트 (벨만 방정식 적용)
        Q_table[current_state, action] += learning_rate * \
            (reward + discount_factor * np.max(Q_table[next_state]) - Q_table[current_state, action])
        
        current_state = next_state  # 다음 상태로 이동

# 학습된 Q-Table 출력
print("학습된 Q-Table:")
print(Q_table)

위 코드를 실행하면 Q-Table이 학습되면서 최적의 행동을 찾아가는 과정을 확인할 수 있습니다.

---

8. Model-Based RL과 Q-Learning의 차이

Q-Learning은 Model-Free RL(모델이 없는 강화학습) 기법입니다.

• 이는 환경의 전이 확률(Transition Probability)이나 보상 함수(Reward Function)를 미리 알 필요 없이, 직접 경험을 통해 최적의 행동을 학습한다는 의미입니다.

• 반면, Model-Based RL(모델 기반 강화학습)은 환경의 동작 모델을 미리 학습하거나 제공받아 이를 활용하여 최적 정책을 도출하는 방식입니다.

비교 항목	Model-Free RL (Q-Learning)	Model-Based RL
환경 모델 저장 여부	❌ (저장 안 함)	✅ (환경 모델 저장)
학습 방식	직접 경험을 통해 학습	환경 모델을 활용한 예측
예측 가능 여부	❌ (미래 상태 예측 불가)	✅ (환경 모델을 통해 예측 가능)
학습 비용	상대적으로 적음	모델 학습과 예측 비용이 큼
예제 알고리즘	Q-Learning, SARSA	다이내믹 프로그래밍(DP), 몬테카를로 트리 탐색(MCTS)

Q-Learning이 Model-Free인 이유

• Q-Learning은 환경의 동작 모델(전이 확률 및 보상 함수)을 직접 학습하지 않고, 환경과의 상호작용을 통해 최적의 행동을 찾습니다.

  • (1) 경험을 통해 Q-값을 업데이트하는 방식을 사용.

  • (2) 환경 모델을 따로 구축하지 않으므로 학습이 더 유연하고 단순.

• 반면, Model-Based RL에서는 환경의 전이 확률과 보상을 모델링하여 미리 예측할 수 있으므로, 실제 환경과의 상호작용 없이도 학습을 진행할 수 있습니다.

(참고) Q-Learning은 환경 모델 없이도 학습할 수 있기 때문에 게임 AI, 로봇 제어, 네트워크 최적화 등 다양한 실제 문제에서 널리 사용됩니다.

---

9. Q-Learning의 한계점(?)

무작정 모든 상태(state)에 대해 Q-Table을 생성하는 것은 낭비일 수 있습니다.

• 특히 상태 공간(state space)이 매우 크거나 연속적인 경우, 테이블 기반 접근 방식은 메모리와 계산 비용이 과도하게 증가하는 문제가 있습니다.

이러한 단점을 극복하기 위해 다양한 연구들이 진행되었으며, 한가지로 함수 근사(Function Approximation) 사용하는 것을 예로 들 수 있습니다.

💡 함수 근사(Function Approximation)란?

• 신경망(Neural Network) 또는 선형 회귀(Linear Regression) 등을 활용하여 Q-Table을 직접 저장하는 대신 함수로 근사하는 방법입니다.
  • 대표적인 알고리즘: Deep Q-Network (DQN)
    • 장점: 상태 공간이 크더라도 메모리 사용량을 줄이고 일반화 가능
    • 단점: 신경망 학습에 시간이 걸리고, 학습 안정성이 떨어질 수 있음

이미지 출처 : 이것저것 테크 블로그 - DQN

(참고) Q-Learning은 고전 강화학습(classic reinforcement learning) 기법 중 하나로 간주됩니다.

• (WHY?) 왜냐하면 Q-learning은 강화학습이 본격적으로 연구되기 시작한 1980~1990년대에 등장한 알고리즘이며, 비교적 단순한 방법으로 상태-행동(State-Action) 값(Q-Value)을 학습하는 방식이기 때문입니다.

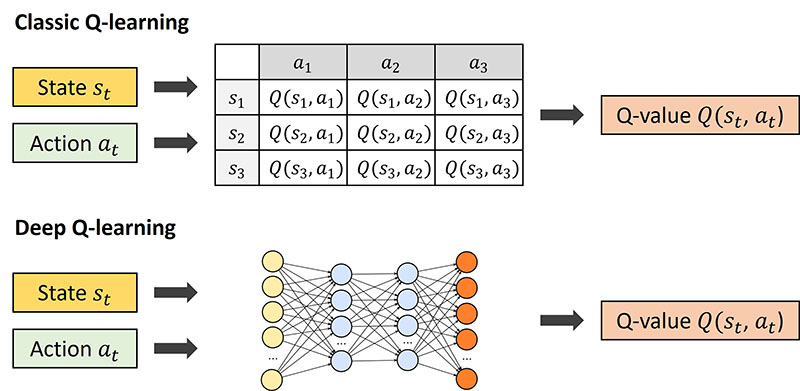
💡 Q-Learning과 Deep Q-Network의 차이

비교 항목	Q-Learning	Deep Q-Network (DQN)
표현 방식	Q-Table(테이블 저장)	신경망(Deep Neural Network)
상태 공간	작거나 이산적(Discrete)	연속적인 공간도 학습 가능
학습 방법	경험을 통한 Q-값 업데이트	신경망을 통해 Q-값 근사
학습 효율성	작은 환경에서는 효율적	복잡한 환경에서도 활용 가능
메모리 사용량	상태가 많아질수록 증가	상태 공간이 커도 학습 가능

✅ 정리

• Q-Learning은 고전적인 강화학습 알고리즘이며, 비교적 단순한 테이블 기반 접근법을 사용합니다.
• Deep Q-Network(DQN) 같은 신경망 기반 강화학습 알고리즘이 등장하면서 더 확장된 형태로 발전했습니다.

---

10. 결론

이번 포스트에서는 혁펜하임님의『Easy! 딥러닝』책을 보면서 더 살펴보고 싶었던 강화학습의 심화내용과, Q-Learning에 대해서 살펴보았습니다.

Q-Learning은 강화학습에서 가장 기본적이고 강력한 알고리즘 중 하나로, 보상을 최대화하는 최적의 행동을 학습할 수 있습니다.

Q-Learning 특징 요약

• Q-Table을 사용하여 학습
• 벨만 방정식 기반으로 Q-값 업데이트
• $\epsilon$-탐욕 정책을 활용하여 탐색과 활용의 균형 유지

Q-Learning의 $Q$라는 용어는 "Action-Value"를 나타내는 기호로, 벨만 방정식에서 유래한 것으로 보는 것이 일반적입니다.

Q-Learning을 충분히 이해하고 나면, 최근 강화학습의 꽃인 심층 강화학습(Deep Q-Network, DQN)으로 확장하여 더 복잡한 문제를 해결할 수도 있습니다. (물론 전 여기까지)

이를 바탕으로 더욱 깊이 있는 학습을 진행해 보시길 바랍니다!

읽어주셔서 감사합니다 😎