(설명추가) 웨이트 초기화 (Weight Initialization)

서쿠·4일 전

도서리뷰 딥러닝

도서리뷰-혁펜하임-Easy딥러닝

목록 보기

4/4

1. 웨이트 초기화란?

딥러닝에서 웨이트 초기화(Weight Initialization)는 신경망의 가중치를 학습 전에 설정하는 과정입니다. 초기화 방식에 따라 모델의 학습 속도, 성능, 안정성이 크게 달라질 수 있습니다.

적절한 초기화 방식은 훈련을 가속화하고, 최적화 과정에서 안정적인 학습을 보장하며, 그래디언트 소실 및 폭발 문제를 방지하는 역할을 합니다.

해당 관련 혁펜하임의 강의가 궁금하다면?

Easy! 딥러닝 웨이트 초기화 기법들 빠르게 정리해 드려요

아래는 위 강의 내용과 제가 추가적으로 조사 및 정리한 내용을 바탕으로 작성한 내용입니다.

웨이트 초기화의 목표

신경망에서 뉴런 $j$ 의 출력(활성화 값) $z_j$ 는 다음과 같이 정의됩니다.

z_j = \sum_{i=1}^{N_{in}} w_{ij} x_i + b_j

여기서, 각각 $x$ , $w$ , $b$ 는 아래를 의미합니다.

$x_i$ 는 이전 층의 출력(또는 입력 데이터)
$w_{ij}$ 는 가중치
$b_j$ 는 편향(bias)

활성화 함수 $f$ 를 적용한 출력은 다음과 같습니다.

a_j = \sigma(z_j)

$z_j$ 는 이전 층의 뉴런 출력을 가중치와 곱한 후 편향을 더한 값 (=선형 변환 결과)
$σ$ 는 시그모이드, 또는 다른 활성화 함수

우리는 각 층에서의 출력 분산을 일정하게 유지하는 웨이트(가중치) 초기화 방법을 찾고자 합니다.

아래 소챕터에서 왜 이러한 웨이트(가중치)가 중요한지 살펴보도록 하겠습니다.

왜 웨이트 초기화가 중요한가?

그래디언트 소실 및 폭발 문제 방지
- 부적절한 초기화는 역전파 과정에서 그래디언트가 0으로 수렴하거나, 너무 커지는 문제를 유발할 수 있습니다.
효율적인 학습 가능
- 초기값이 적절하면 학습이 빠르게 진행되며, 최적의 손실값을 찾는 데 도움이 됩니다.
활성화 함수의 특성 유지
- 각 층의 출력값이 활성화 함수의 적절한 범위를 유지할 수 있도록 도와줍니다.
초기 수렴 속도 향상
- 적절한 초기화는 학습 초기에 손실 함수의 감소를 촉진하여 더 빠르게 수렴할 수 있도록 합니다.

2. 네트워크 초기화란?

딥러닝 모델의 네트워크 초기화(Network Initialization)는 모델 내 모든 레이어의 가중치를 초기화하는 과정입니다. 초기화 방법을 신중하게 선택하지 않으면 학습이 비효율적으로 진행될 수 있습니다.

MLP (Multi-Layer Perceptron): 모든 Fully Connected Layer (선형층) 의 가중치를 초기화
CNN (Convolutional Neural Networks): 합성곱 필터(Convolution Kernel) 전부 초기화
RNN (Recurrent Neural Networks): 순환층(Recurrent Layers) 및 연결 가중치 초기화
Transformer 계열 모델: 모든 Self-Attention Layer와 FFN Layer 초기화

따라서, 네트워크 초기화는 단순히 일부 가중치를 랜덤하게 설정하는 것이 아니라, 모든 레이어의 가중치를 특정 방식으로 초기화하는 과정을 의미합니다. 일부 초기화 기법은 특정 활성화 함수와 조합하여 사용해야 최적의 성능을 발휘할 수 있습니다.

💻 (참고) 분산 증가와 시그모이드의 포화 현상
신경망에서 가중치 초기화가 중요한 이유 중 하나는 활성화 함수의 특성과 학습 안정성 때문입니다. 특히 시그모이드(Sigmoid)와 같은 활성화 함수를 사용할 경우, 가중치 초기화가 적절하지 않으면 분산이 커져 포화(Saturation) 문제가 발생할 수 있습니다.

1. 시그모이드 함수의 특성
시그모이드 함수는 입력값 $z$ 에 대해 다음과 같이 정의됩니다.

\sigma(z) = \frac{1}{1 + e^{-z}}

이 함수의 중요한 특성은:

$z$ 가 매우 크면 $\sigma(z) \approx 1$
$z$ 가 매우 작으면 $\sigma(z) \approx 0$
$z = 0$ 일 때 $\sigma(0) = 0.5$

즉, 입력값이 너무 크거나 작아지면 시그모이드의 출력이 0 또는 1로 수렴하면서 미분값이 0에 가까워지는 포화 현상이 발생합니다.

2. 분산 증가와 포화 현상
출력 뉴런의 활성화 값 $z_j$ 는 다음과 같이 계산됩니다.

z_j = \sum_{i=1}^{N_{in}} w_{ij} x_i + b_j

여기서 $x_i$ 는 입력값이고, $w_{ij}$ 는 가중치입니다. 만약 입력값과 가중치가 독립적인 정규 분포를 따른다면, 중앙극한정리(CLT)에 의해 $z_j$ 도 정규 분포를 따르게 됩니다.

z_j \sim \mathcal{N}(0, N_{in} \cdot \sigma_x^2 \cdot \sigma_w^2)

즉, 입력 개수 $N_{in}$ 이 커질수록 $z_j$ 의 분산이 증가하게 됩니다.

이 경우, $z_j$ 값이 극단적으로 커질 확률이 높아지고, 시그모이드 출력값이 0 또는 1로 수렴하는 포화 영역에 들어가게 됩니다.

3. 포화 현상이 발생하면?

Vanishing Gradient(기울기 소실)
- 시그모이드 함수의 미분은 $\sigma'(z) = \sigma(z) (1 - \sigma(z))$ 이므로, $\sigma(z) \approx 0$ 또는 $\sigma(z) \approx 1$ 일 때 미분값이 0에 가까워집니다.
- 이로 인해 역전파(Backpropagation) 과정에서 기울기가 소실되어 신경망 학습이 어려워집니다.
학습 속도 저하
- 대부분의 뉴런이 0 또는 1로 고정되면서, 뉴런이 활성화되지 않는 죽은 뉴런 문제(Dead Neuron Problem)가 발생할 수 있습니다.

4. 해결 방법: 적절한 가중치 초기화 기법

이러한 문제를 해결하기 위해, 가중치의 초기 분산을 조절하는 다양한 초기화 기법이 제안되었습니다.

다음과 같은 방법을 사용하면 분산이 너무 커지지 않도록 조정하여 포화 문제를 방지할 수 있습니다.

LeCun 초기화 ( $w \sim N(0, \frac{1}{N_{in}})$ )
- 주로 Sigmoid, Tanh 같은 비선형 활성화 함수에 사용됨.
Xavier (Glorot) 초기화 ( $w \sim N(0, \frac{2}{N_{in} + N_{out}})$ )
- 입력과 출력의 개수를 고려하여 가중치를 조정하여 안정적인 학습을 유도.
He (Kaiming) 초기화 ( $w \sim N(0, \frac{2}{N_{in}})$ )
- ReLU 계열 활성화 함수에 적합하며, 입력 개수를 고려하여 분산을 조정.

💌 신경망 학습의 안정성을 위해 적절한 가중치 초기화 방법이 필요합니다. 잘못된 초기화는 분산 증가(Variance Explosion) 또는 기울기 소실(Vanishing Gradient) 문제를 일으킬 수 있습니다. 따라서, 가중치를 적절히 초기화하여 순전파(Forward Propagation)와 역전파(Backward Propagation)에서 신호의 분산을 일정하게 유지하는 것이 중요합니다.

이는 아래 3. 주요 웨이트 초기화 방법에서 자세하게 살펴보겠습니다.

3. 주요 웨이트 초기화 방법

3.0 PyTorch 및 Keras 초기화 모듈

PyTorch의 torch.nn.init과 Keras의 tensorflow.keras.initializers 모듈은 다양한 초기화 방법을 제공합니다. 이를 활용하면 신경망의 각 층에 맞는 적절한 초기화를 쉽게 적용할 수 있습니다.

📌 PyTorch 초기화 모듈

import torch.nn.init as init

# 기본적인 초기화 방법
init.uniform_(tensor)  # 균등 분포 초기화
init.normal_(tensor)   # 정규 분포 초기화
init.xavier_uniform_(tensor)  # Xavier 균등 초기화
init.kaiming_uniform_(tensor, nonlinearity='relu')  # He 초기화
init.orthogonal_(tensor)  # 직교 초기화
init.constant_(tensor, 0)  # 상수 초기화

📌 Keras 초기화 모듈

from tensorflow.keras.initializers import *

initializer = GlorotUniform()  # Xavier 초기화
initializer = HeNormal()  # He 초기화
initializer = Orthogonal(gain=1.0)  # 직교 초기화

3.1 LeCun 초기화

제안자: Yann LeCun (1998)
사용 활성화 함수: Sigmoid, Tanh, SELU
초기화 공식:
$w \sim N(0, \frac{1}{N_{in}})$
- $N_{in}$ : 입력 노드 수

LeCun 초기화는 sigmoid 및 tanh 활성화 함수에 적합하도록 설계되었습니다.

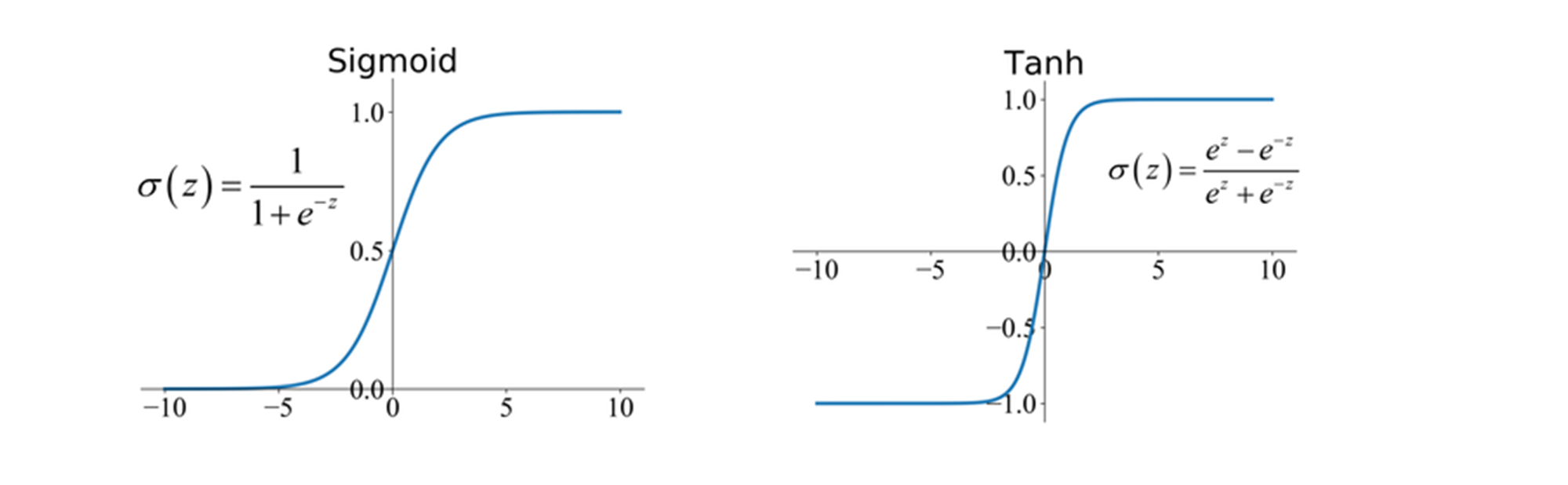
(참고) sigmoid 및 tanh 활성화 함수

Sigmoid 함수

\sigma(z) = \frac{1}{1 + e^{-z}}

출력 범위: (0, 1)
기울기(미분): $\sigma'(z) = \sigma(z) (1 - \sigma(z))$
분석:
- $z$ 값이 크면 $\sigma(z) \approx 1$ , $z$ 값이 작으면 $\sigma(z) \approx 0$ 이 되어 출력이 거의 변하지 않음 (포화).
- 포화된 영역에서는 기울기 $\sigma'(z)$ 가 거의 0이 되어 기울기 소실(Vanishing Gradient) 문제가 발생.

Tanh 함수

\tanh(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}}

출력 범위: (-1, 1)
기울기(미분): $\tanh'(z) = 1 - \tanh^2(z)$
분석:
- $|z|$ 값이 크면 $\tanh(z) \approx \pm1$ 로 수렴하여 기울기 $\tanh'(z) \to 0$ .
- 역시 기울기 소실 문제가 발생.

💬 위에서 살펴볼 수 있다시피, Sigmoid는 중앙에서 최대 기울기가 0.25로 제한되며, Tanh는 $z = 0$ 에서 1이지만 $|z|$ 가 증가할수록 기울기가 0에 수렴하기 때문에,

초기 가중치가 너무 크면 분산 증가로 인해 활성화 값이 포화 상태에 도달하여 기울기 소실 문제가 발생할 수 있습니다.

반대로, 초기 가중치가 너무 작으면 모든 뉴런의 출력이 거의 0 또는 -1 근처로 몰리면서 기울기 역시 작아져 학습이 비효율적으로 이루어질 수 있습니다.

$z_j$ 의 분산 증가

신경망에서 뉴런의 활성화 값 $z_j$ 는 다음과 같이 정의됩니다.
$z_j = \sum_{i=1}^{N_{in}} w_{ij} x_i + b_j$
여기서 가중치 $w_{ij}$ 가 큰 분산을 가지면, $z_j$ 의 분산도 증가합니다.
- 만약 $w_{ij} \sim \mathcal{N}(0, \sigma_w^2)$ 이라면: $\text{Var}[z_j] = N_{in} \cdot \text{Var}[w] \cdot \text{Var}[x]$
즉, 가중치의 분산이 클수록 $z_j$ 의 분산도 커지게 됨.

💡 LeCun 초기화가 이를 어떻게 방지하는가?

LeCun 초기화는 가중치의 분산을 작게 설정하여 $z_j$ 가 포화 영역에 도달하지 않도록 합니다.
LeCun 초기화는 작은 분산( $\frac{1}{N_{in}}$ )을 사용하여 시그모이드 및 Tanh의 포화 문제를 방지합니다.
- LeCun 초기화를 사용하면 → $z$ 값이 0 근처에 머무름 → 활성화 함수가 기울기를 유지하여 안정적으로 학습됨
LeCun 초기화 (2종류)
- 정규분포를 따르는 경우: $w_{ij} \sim \mathcal{N}(0, \frac{1}{N_{in}})$
- 균등분포를 따르는 경우: $w_{ij} \sim \mathcal{U} \left(-\frac{1}{\sqrt{N_{in}}}, \frac{1}{\sqrt{N_{in}}} \right)$

아래는 파이토치와 케라스에 적용한 예시 코드입니다.

📌 적용 예시 (PyTorch)

import torch.nn as nn
import torch.nn.init as init

def init_weights(m):
    if isinstance(m, nn.Linear):
        init.normal_(m.weight, mean=0, std=1 / m.in_features)
        init.zeros_(m.bias)

model.apply(init_weights)

📌 적용 예시 (Keras)

from tensorflow.keras.layers import Dense
from tensorflow.keras.initializers import LecunNormal

layer = Dense(64, activation='selu', kernel_initializer=LecunNormal())

3.2 Xavier (Glorot) 초기화

제안자: Xavier Glorot & Yoshua Bengio (2010)
사용 활성화 함수: Sigmoid, Tanh
초기화 공식:
$w \sim N(0, \frac{2}{N_{in} + N_{out}})$
- $N_{in}$ : 입력 노드 수
- $N_{out}$ : 출력 노드 수

(참고) sigmoid 및 tanh 활성화 함수

LeCun 초기화는 순전파에서 $z$ 값이 너무 커지는 것을 방지하기 위해 가중치 분산을 $\frac{1}{N_{in}}$ 으로 설정.
- 그러나 역전파 시 기울기(gradient) 분산까지 고려하지 않음.
Xavier 초기화는 역전파 과정에서도 기울기의 분산이 일정하게 유지되도록 개선하였으며,
- 출력 노드 개수 $N_{out}$ 까지 고려하여 분산을 줄임.
- 즉, 신호가 네트워크를 통해 전파될 때 손실되지 않고 안정적으로 유지되도록 설계됨.

💡 즉, Xavier 초기화는 LeCun 초기화의 개념을 확장하여, 순전파뿐만 아니라 역전파에서도 분산이 일정하게 유지되도록 개선한 방식입니다.

아래는 파이토치와 케라스에 적용한 예시 코드입니다.

📌 적용 예시 (PyTorch)

def init_weights(m):
    if isinstance(m, nn.Linear):
        init.xavier_uniform_(m.weight)
        init.zeros_(m.bias)

model.apply(init_weights)

📌 적용 예시 (Keras)

from tensorflow.keras.layers import Dense
from tensorflow.keras.initializers import GlorotUniform

layer = Dense(64, activation='tanh', kernel_initializer=GlorotUniform())

3.3 He (Kaiming) 초기화

제안자: Kaiming He (2015)
사용 활성화 함수: ReLU, Leaky ReLU
초기화 공식:
$w \sim N(0, \frac{2}{N_{in}})$
- $N_{in}$ : 입력 노드 수

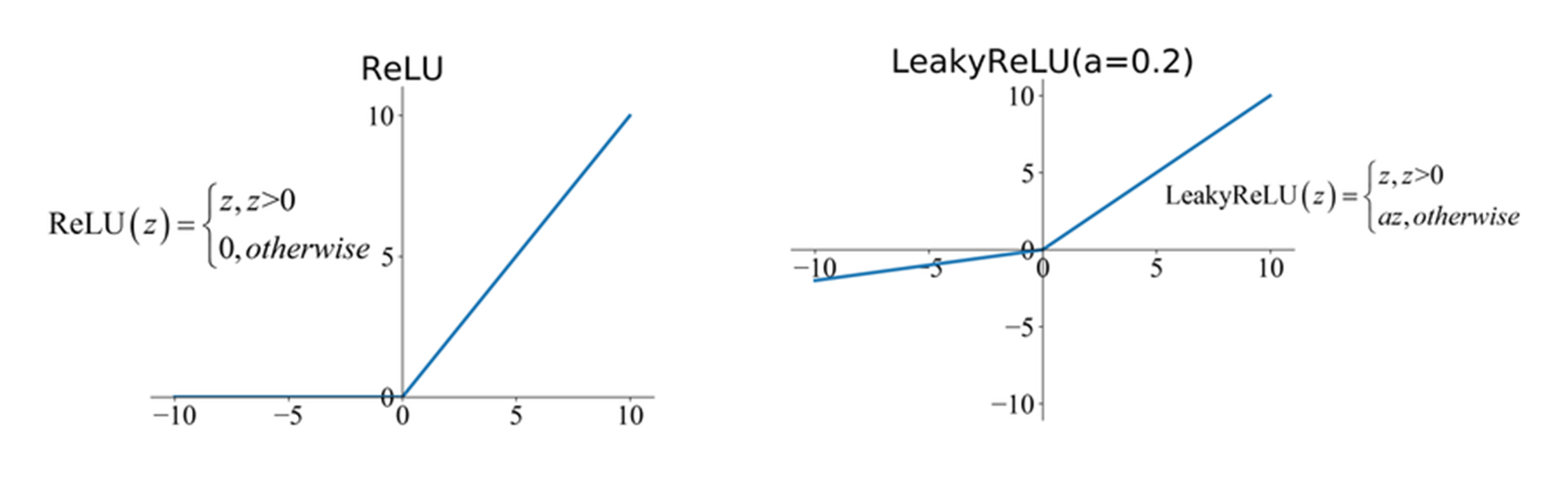
(참고) ReLU 및 Leaky ReLU 활성화 함수

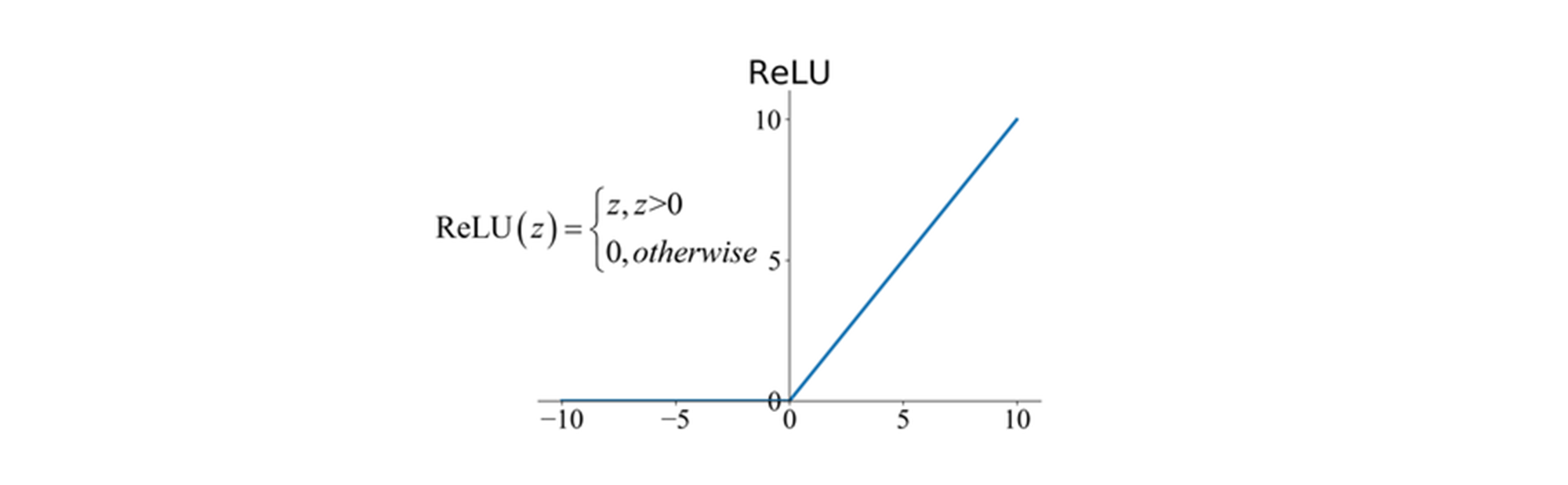
(1) ReLU: 비대칭적인 활성화 함수

ReLU는 음수를 모두 0으로 만드는 특성이 있습니다.

\text{ReLU}(x) = \max(0, x)

즉,

입력값이 양수일 경우: 그대로 전달됨.
입력값이 음수일 경우: 0으로 변함.

뉴런 절반이 비활성화됨 (Dead Neurons 문제)
- 음수 입력을 받는 뉴런은 항상 0을 출력 → 학습 과정에서 뉴런이 죽어버릴 가능성 높음.
출력값이 한쪽으로 편향됨 → 분산이 감소할 가능성
- Xavier 초기화처럼 $\frac{1}{N_{in} + N_{out}}$ 또는 $\frac{1}{N_{in}}$ 을 사용하면 분산이 너무 작아져, ReLU가 제대로 활성화되지 않을 수 있음.

(2) Leaky ReLU: 완화된 형태이지만 여전히 편향 문제 존재

Leaky ReLU는 ReLU의 Dead Neurons 문제를 완화하기 위해 음수 입력에도 작은 기울기 $\alpha$ 를 적용한 변형입니다.

\text{Leaky ReLU}(x) = \begin{cases} x, & \text{if } x \geq 0 \\ \alpha x, & \text{if } x < 0 \end{cases}

그러나 Leaky ReLU도 여전히 출력값이 한쪽으로 편향되는 문제가 발생할 수 있기 때문에 적절한 가중치 초기화가 필요합니다.

💡 He (Kaiming) 초기화의 탄생 비화

(1) Xavier 초기화의 한계점

Xavier 초기화는 시그모이드 및 Tanh 활성화 함수를 위해 설계되었으며, 다음과 같은 분산을 사용합니다.

\text{Var}[w] = \frac{2}{N_{in} + N_{out}}

그러나 Xavier 초기화는 ReLU 활성화 함수를 고려하지 않았기 때문에, ReLU에서는 신경망이 올바르게 학습되지 않을 가능성이 있습니다.
- Xavier 초기화는 출력값이 평균 0을 유지하도록 설계되었으나,
- ReLU는 출력값이 항상 0 이상이므로 평균이 0보다 큼 → Xavier 초기화를 적용하면 출력값이 너무 작아지는 문제가 발생할 수 있음.
즉, Xavier 초기화는 ReLU에서 출력값의 크기가 급격히 작아질 가능성이 높음.

(2) He 초기화에서 2를 곱하는 이유

He 초기화는 ReLU 계열 활성화 함수의 비대칭성을 고려하여 가중치의 분산을 더 크게 설정합니다.

\text{Var}[w] = \frac{2}{N_{in}}

즉, LeCun 초기화보다 2배 큰 분산을 사용합니다.

🤔 Q. 왜 LeCun 초기화보다 2배 큰 분산을 사용하는가?

ReLU는 음수 출력을 0으로 만들기 때문에 평균이 줄어듦
- Xavier 초기화에서는 평균이 0을 유지하는 것이 목표지만,
- ReLU는 음수를 모두 0으로 보내므로 출력 평균이 0보다 커지게 됨.
- 따라서 분산이 너무 작아질 수 있음.
출력값의 분산 감소를 보정하기 위해 2배 증가
- ReLU는 입력의 약 절반만 활성화됨 → 활성화된 뉴런들만 고려하면 평균이 낮아짐.
- 이를 보정하기 위해 가중치의 분산을 2배 증가시켜 학습을 원활하게 진행할 수 있도록 함.

=> 즉, He 초기화는 ReLU 뉴런이 비활성화되는 특성을 고려하여 적절한 분산을 조절한 방법이라고 할 수 있습니다.

아래는 파이토치와 케라스에 적용한 예시 코드입니다.

📌 적용 예시 (PyTorch)

def init_weights(m):
    if isinstance(m, nn.Conv2d) or isinstance(m, nn.Linear):
        init.kaiming_uniform_(m.weight, nonlinearity='relu')
        init.zeros_(m.bias)

model.apply(init_weights)

📌 적용 예시 (Keras)

from tensorflow.keras.layers import Dense
from tensorflow.keras.initializers import HeNormal

layer = Dense(64, activation='relu', kernel_initializer=HeNormal())

정리

각 초기화 방법이 어떻게 분산을 조절하는지 정리하면 다음과 같습니다.

초기화 기법	가중치 분포	사용되는 활성화 함수	특징
LeCun 초기화	$w \sim \mathcal{N}(0, \frac{1}{N_{in}})$	Sigmoid, Tanh	Sigmoid 포화 문제 방지
Xavier (Glorot) 초기화	$w \sim \mathcal{N}(0, \frac{2}{N_{in} + N_{out}})$	Sigmoid, Tanh	순전파 및 역전파에서 분산 유지
He (Kaiming) 초기화	$w \sim \mathcal{N}(0, \frac{2}{N_{in}})$	ReLU, Leaky ReLU	ReLU 활성화 뉴런 비율 보정

각 초기화 기법은 순전파와 역전파에서 분산이 너무 커지거나 작아지는 문제를 방지하기 위해 설계되었습니다.

4. 초기화 방법 선택 기준

초기화 방식에 따라 학습 성능이 크게 달라질 수 있습니다.

따라서 사용하려는 활성화 함수와 네트워크 구조에 맞춰 적절한 초기화 방법을 선택하는 것이 중요합니다.

🙌 아래는 초기화 방법 선택 시 고려해야 할 팁입니다:

활성화 함수와의 조합 고려:
- 활성화 함수에 따라 최적의 초기화 방법이 다릅니다.
- 예를 들어, ReLU 계열 함수에는 He 초기화가, Sigmoid나 Tanh 함수에는 Xavier 초기화가 적합합니다.
네트워크 깊이와 구조에 따른 조정:
- 네트워크가 깊어질수록 그래디언트 소실이나 폭발 문제가 발생할 수 있습니다.
- 이를 완화하기 위해 각 층의 가중치 초기화를 신중하게 설정해야 합니다.
배치 정규화와의 병행 사용:
- 배치 정규화(Batch Normalization)는 각 층의 입력 분포를 정규화하여 학습을 안정화시킵니다.
- 초기화와 함께 사용하면 더 나은 성능을 얻을 수 있습니다.
드롭아웃과의 상호작용:
- 드롭아웃(Dropout)을 사용하는 경우, 가중치 초기화가 드롭아웃의 효과에 영향을 줄 수 있습니다.
- 이때는 초기화 방법을 적절히 선택하여 드롭아웃과의 시너지를 극대화해야 합니다.
학습률과 초기화의 상관관계:
- 가중치 초기화에 따라 최적의 학습률이 달라질 수 있습니다. 초기화 방법을 선택한 후, 이에 맞는 학습률을 설정하는 것이 중요합니다.
정규화 기법과의 조합:
- L1, L2 정규화와 같은 기법과 초기화를 함께 사용하여 과적합을 방지하고 일반화 성능을 향상시킬 수 있습니다.
초기화 방법의 실험적 검증:
- 모델과 데이터셋에 따라 최적의 초기화 방법이 다를 수 있으므로, 여러 초기화 방법을 실험하여 가장 적합한 방식을 선택하는 것이 좋습니다.

이러한 팁들을 고려하여 웨이트 초기화를 설정하면 딥러닝 모델의 학습 효율성과 성능을 더욱 향상시킬 수 있습니다.

❓ (참고) 웨이트를 0 또는 1로 설정하면 어떤 문제가 발생할 수 있나요?

웨이트를 0 또는 1로 초기화하면 문제가 발생할 수 있습니다.

0으로 설정할 경우: 모든 뉴런이 동일한 출력과 동일한 그래디언트를 가지게 되며, 학습이 진행되지 않음.

1로 설정할 경우: 그래디언트가 너무 크거나 너무 작아질 수 있으며, 네트워크가 제대로 학습되지 않음.

랜덤 초기화의 필요성: 뉴런들이 각기 다른 특징을 학습할 수 있도록 가중치를 무작위로 초기화해야 함.

❓(참고) 그러면 일반 정규분포는 전혀 안 쓰나요?

파이토치에서 torch.nn.init.normal_ 함수는 텐서의 값을 정규 분포(Normal Distribution)를 따르도록 초기화하는 데 사용됩니다.

이 함수는 평균(mean)과 표준편차(std)를 지정하여, 해당 분포에 따라 텐서의 요소들을 무작위로 설정합니다.

일반적으로, 딥러닝 모델의 가중치 초기화 시에는 활성화 함수와 네트워크 구조에 최적화된 초기화 방법이 권장됩니다.

예를 들어, ReLU 활성화 함수에는 He 초기화, Sigmoid나 Tanh 함수에는 Xavier 초기화가 적합합니다. 이러한 방법들은 각 층의 입력 및 출력 노드 수를 고려하여 가중치를 초기화함으로써, 학습의 안정성과 수렴 속도를 향상시킵니다.

반면에, torch.nn.init.normal_과 같은 일반적인 정규 분포 초기화는 이러한 최적화된 초기화 방법에 비해 학습 효율이 떨어질 수 있습니다. 따라서, 특정한 이유나 실험적인 목적이 없는 한, 일반적인 정규 분포 초기화는 많이 사용되지 않습니다.

그러나, 특정한 모델이나 실험에서는 torch.nn.init.normal_을 사용할 수 있습니다.

예를 들어, GAN(Generative Adversarial Network) 모델의 구현에서 가중치를 초기화할 때, 평균이 0이고 표준편차가 0.02인 정규 분포를 사용하기도 합니다.

5. 결론

웨이트 초기화는 딥러닝 모델의 첫걸음을 결정짓는 중요한 요소입니다.

적절한 초기화를 선택하면 학습이 안정적으로 진행되고, 그래디언트 소실이나 폭발 같은 문제도 줄일 수 있습니다.

쉽게 정리하면 다음과 같습니다:

ReLU 계열 → He 초기화
Sigmoid, Tanh → Xavier 초기화
SELU → LeCun 초기화

모델을 처음부터 제대로 세팅하면 학습 속도도 빨라지고, 원하는 성능을 더 쉽게 얻을 수 있습니다.

읽어주셔서 감사합니다! 😊✨

서쿠

Always be passionate ✨

이전 포스트

(설명추가) 웨이트 초기화 (Weight Initialization)

도서리뷰-혁펜하임-Easy딥러닝

1. 웨이트 초기화란?

웨이트 초기화의 목표

왜 웨이트 초기화가 중요한가?

2. 네트워크 초기화란?

3. 주요 웨이트 초기화 방법

3.0 PyTorch 및 Keras 초기화 모듈

📌 PyTorch 초기화 모듈

📌 Keras 초기화 모듈

3.1 LeCun 초기화

📌 적용 예시 (PyTorch)

📌 적용 예시 (Keras)

3.2 Xavier (Glorot) 초기화

📌 적용 예시 (PyTorch)

📌 적용 예시 (Keras)

3.3 He (Kaiming) 초기화

📌 적용 예시 (PyTorch)

📌 적용 예시 (Keras)

4. 초기화 방법 선택 기준

5. 결론

(설명추가) Q-Learning: 강화학습의 핵심 개념과 이해

0개의 댓글

관련 채용 정보