오늘은 파이토치를 다루기 위해 중요한 기초 지식들 중 텐서에 대해 다루어볼 예정입니다.
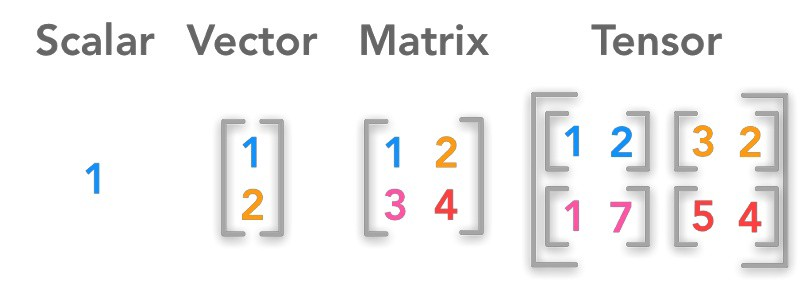
Source : https://hadrienj.github.io/posts/Deep-Learning-Book-Series-2.1-Scalars-Vectors-Matrices-and-Tensors/
텐서
- 텐서는 '데이터를 표현하는 단위'입니다.
- 크게
scalar,vector,matrix,tensor로 분류할 수 있습니다.
Scalar
- 스칼라(scalar)는 우리가 흔히 수학에서 부르는 상수 값이라고 보면 됩니다.
- Pytorch 모듈에서 이를 활용해주기 위해서는 아래와 같이 import torch 후 torch 모듈에 내장되어 있는 tensor 메서드를 이용해 다음과 같이 스칼라 값을 정의해줄 수 있습니다.
💻 코드
import torch
# 텐서 메서드를 이용해 스칼라 값 정의
scalar = torch.tensor([2.])
print(scalar) # 값 출력
print(scalar.shape) # 사이즈 출력💻 결과
tensor([2.])
torch.Size([1])※ 여기서 잠깐 ※
💡 [스칼라의 연산]
스칼라는 우리가 흔히 알고 있는+,-,*,/의 사칙연산 기호 또는 torch 모듈의 내장된 메서드인add,sub,mul,div을 이용하여 사칙연산을 수행할 수 있습니다.
Vector
- 벡터(vector)는 수학 개념으로 크기와 방향을 갖는 물리량을 의미합니다.
- 일반적으로 벡터는 시작점과 끝점을 연결하는 화살표로 표시할 수 있는데, 시작점을 (0,)이라고 하면 벡터는 n차원 공간 상의 좌표라고 생각할 수도 있습니다.
- Pytorch 모듈에서 이를 활용해주기 위해서는 아래와 같이 import torch 후 torch 모듈에 내장되어 있는 tensor 메서드를 이용해 다음과 같이 벡터를 정의해줄 수 있습니다.
💻 코드
import torch
# 텐서 메서드를 이용해 벡터 정의
vector = torch.tensor([1., 2., 3.])
print(vector) # 값 출력
print(vector.shape) # 사이즈 출력💻 결과
tensor([1., 2., 3.])
torch.Size([3])※ 여기서 잠깐 ※
💡 [벡터의 연산]
벡터 역시 우리가 흔히 알고 있는+,-,*,/의 사칙연산 기호 또는 torch 모듈의 내장된 메서드인add,sub,mul,div을 이용하여 사칙연산을 수행할 수 있습니다. 여기서 주의해야 할 점은 곱셈과 나눗셈의 경우 각 요소별로(element-wise) 연산을 수행하게 됩니다. 스칼라 연산에서 한가지 추가되는 것이 있는 데 바로 내적입니다. 내적은 torch 모듈의 내장된 메서드인dot을 이용해서 사용하실 수 있습니다.
Matrix
- 행렬(matrix)이란 실수 또는 복소수를 위 그림의 좌변과 같이 직사각형으로 배열한 것을 말합니다. 즉, 이 말은 2개 이상의 벡터를 합쳐서 구성한 것이 곧 행렬이 되게 됩니다.
- 행렬은 벡터 간 연산을 빠르게 진행할 수 있는 선행 대수의 기본 단위입니다.
- Pytorch 모듈에서 이를 활용해주기 위해서는 아래와 같이 import torch 후 torch 모듈에 내장되어 있는 tensor 메서드를 이용해 다음과 같이 행렬을 정의해줄 수 있습니다.
💻 코드
import torch
# 텐서 메서드를 이용해 행렬 정의
matrix = torch.tensor([[1., 2.],[3., 4.]])
print(matrix) # 값 출력
print(matrix.shape) # 사이즈 출력💻 결과
tensor([[1., 2.],
[3., 4.]])
torch.Size([2, 2])※ 여기서 잠깐 ※
💡 [행렬의 연산]
행렬 역시 우리가 흔히 알고 있는+,-,*,/의 사칙연산 기호 또는 torch 모듈의 내장된 메서드인add,sub,mul,div을 이용하여 사칙연산을 수행할 수 있습니다. 여기서 주의해야 할 점은 곱셈과 나눗셈의 경우 각 요소별로(element-wise) 연산을 수행하게 됩니다. 스칼라 연산에서 한가지 추가되는 것이 있는 데 바로 행렬 곱 연산입니다. 내적은 torch 모듈의 내장된 메서드인matmul을 이용해서 사용하실 수 있습니다. matmul은 matrix multiply의 줄임말입니다.
Tensor
- 텐서(tensor)란 매우 수학적인 개념으로 데이터의 배열이라고 볼 수 있습니다.
- 텐서는 엄밀히 말하면 앞에서 소개한 scalar, vector, matrix 모두를 아우르는 개념이며 아래의 표와 같이 정리될 수 있습니다. (왜 여태까지 scalar, vector, matrix를 선언하는 데 torch.tensor를 썻는지 아시겠죠?ㅎㅎ)
| RANK | TYPE | EXAMPLE |
|---|---|---|
| 0 | scalar | [1] |
| 1 | vector | [1,2] |
| 2 | matrix | [[1,2],[3,4]] |
| 3 | 3d-tensor | [[[1,2],[3,4]],[[5,6],[7,8]]] |
| n | nd-tensor | [[[1,2],[3,4]],[[5,6],[7,8]], ...] |
- 다음은 스칼라, 벡터, 행렬, 텐서를 그림으로 표현한 것입니다.

Source : https://hadrienj.github.io/posts/Deep-Learning-Book-Series-2.1-Scalars-Vectors-Matrices-and-Tensors/
- Pytorch 모듈에서 이를 활용해주기 위해서는 아래와 같이 import torch 후 torch 모듈에 내장되어 있는 tensor 메서드를 이용해 다음과 같이 텐서를 정의해줄 수 있습니다.
💻 코드
import torch
# 텐서 메서드를 이용해 tensor 정의
tensor_ = torch.tensor([[[1,2],[3,4]],[[5,6],[7,8]]])
print(tensor_) # 값 출력
print(tensor_.shape) # 사이즈 출력💻 결과
tensor([[[1, 2],
[3, 4]],
[[5, 6],
[7, 8]]])
torch.Size([2, 2, 2])※ 여기서 잠깐 ※
💡 [텐서의 연산]
텐서의 연산은 행렬의 확장판이기에 동일합니다.

