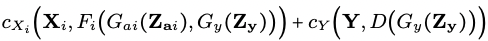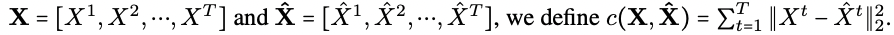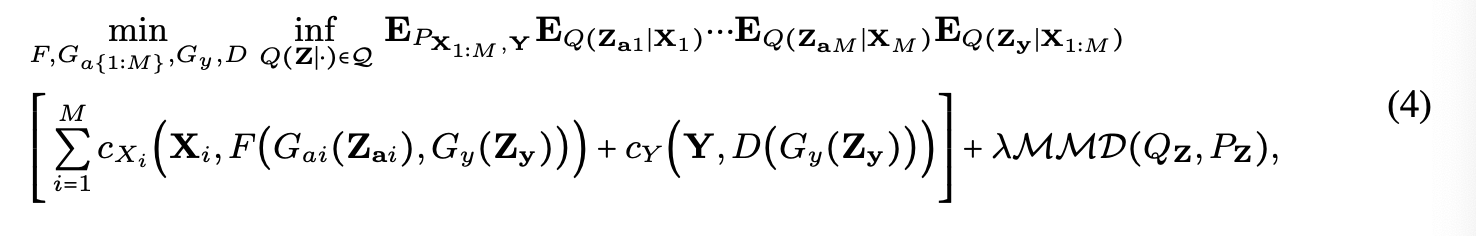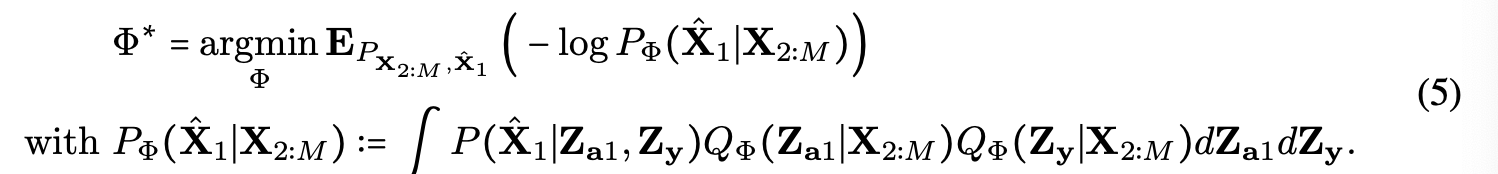[발표용] Learning Factorized Multimodal Representations

Eun·2023년 2월 19일

study

목록 보기

2/2

ICLR 2019

Learning Factorized Multimodal Representations

논문 세 줄 요약

1) Multimodal representation learning을 잘 하기 위한 Multimodal Factorization Model(MFM)을 제안

MFM의 장점) 좋은 multimodal representation을 학습할 수 있음

2) MFM은 multimodal representaion을 multimodal discriminative factors와 modality-specific generative factors로 factorize(분해)함

기여점) 기존 연구들은 두 discriminative factor와 generative factor 중 하나만 사용했는데 이번 연구에서는 둘 다 사용했다.
그리고 generative facotr도 각 모달별 factor로 또 분해해서 사용했다.

3) 그래서 우리 모델은 분류와 생성을 모두 잘한다!

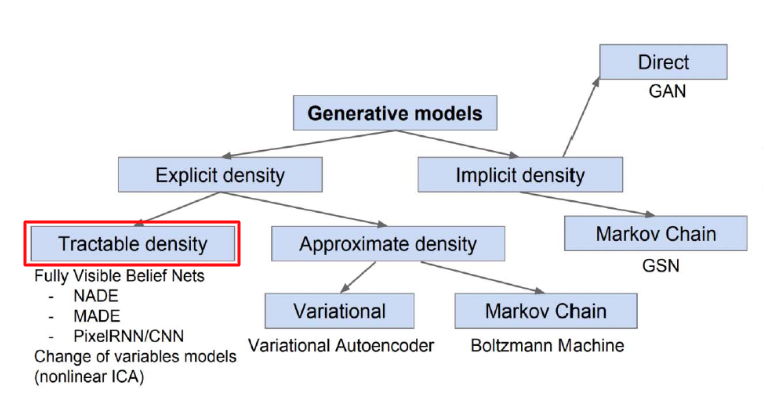
Background

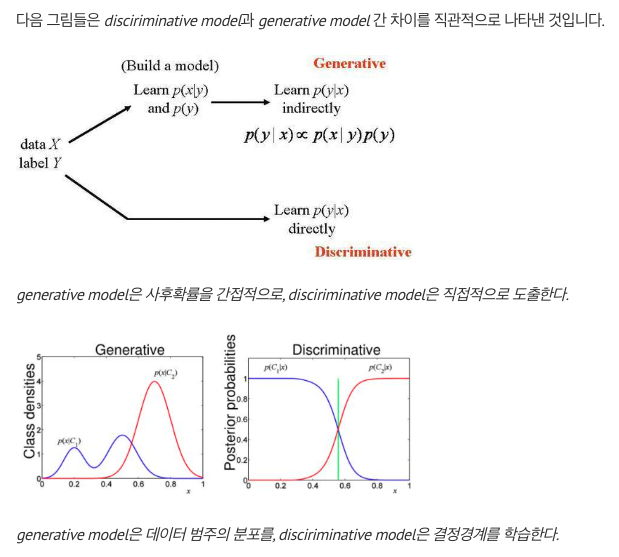
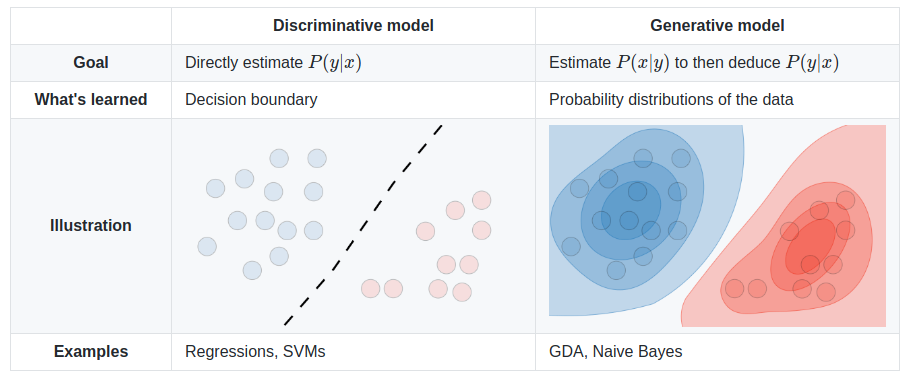
Discriminative model

데이터 $𝑋$ 가 주어졌을 때 라벨 $𝑌$ 가 나타날 조건부 확률 $P(𝑌|𝑋)$ 를 직접적으로 반환하는 모델

$Y$ 를 잘 구분하는 결정경계를 학습하는 것이 목표 (supervised learning)

대표적인 예시) 선형회귀, 로지스틱회귀

Generative model

데이터 𝑋가 생성되는 과정을 두 개의 확률모형 $(P(𝑌), P(𝑋|𝑌))$ 으로 정의하고, 베이즈룰을 사용해 $P(𝑌|𝑋)$ 를 간접적으로 도출하는 모델

분포를 학습하는 것이 목표

$P(𝑋|𝑌)$ 를 구축하기 때문에 X를 생성 할 수 있음

레이블 Y가 있으면 supervised, 없으면 unsupervised

대표적인 예시) 가우시안믹스처 모델, 토픽 모델링

Multimodal representation learning의 두 가지 주요 pillar(기둥, 방향)는 Discriminative와 Generative였음

이전까지는 Discriminative objectives와 generative objectives를 각각 고려했음

1. Discriminative representation learning
Conditional distribution $P(Y|X_{1:M})$ 를 모델링함
이 방법은 $P(X_{1:M})$ 를 명시적으로 모델링하지 않아도 되기 때문에 효율적으로 파라미터를 사용할 수 있음

Tsai & Salakhutdinov, 2017
one-shot image recognition을 향상하기 위해 linguistic attributes에 최대로 의존하는 visual representations을 학습
Liu et al., 2018; Zadeh et al., 2017
language와 visual 그리고 acoustic modalities 사이의 interactions을 모델링하기 위한 tensor product mechanism을 소개함
-> 세정님이 첫 주차에 발표하신 논문!! (https://asidefine.tistory.com/203)

2. Generative representation learning
joint distribution $P(X_1, ... , X_M)$ 를 모델링하여 modalities 간의 interactions를 포착

unidirected graphical model (Srivastava & Salakhutdinov, 2012)
directed graphical model (Suzuki et al., 2016b)
neural network (Sohn et al., 2014)

(Pham et al.,2018; Ngiam et al., 2011)
multimodal data를 discriminative tasks에서 사용되는 lower-dimensional feature vectors로 압축하는 방법

MFM은 두 접근 방법의 장점을 통합하기 위해 아래의 두 방법을 사용
1) multimodal representations을 generative와 discriminative components로 factorizes
2) joint objective를 최적화

Factorized representation learning
분리된 data representations을 학습하여 task를 향상을 시키는 것과 유사함 (Kulkarni et al., 2015; Lake et al., 2017; Higgins et al., 2016; Bengio et al., 2013)

Latent value를 지정하고 supervised learning 진행
(Cheung et al., 2014; Karaletsos et al., 2015; Yang et al., 2015; Reed et al., 2014; Zhu et al., 2014)
Latent value에 isotropic Gaussian prior를 가정하고 disentangled generative representations을 학습 (Kingma & Welling, 2013; Rubenstein et al., 2018)
예) 얼굴 표현에서 얼굴 표정, 눈 색깔, 머리 모양, 안경의 유무, 해당 사람의 신원과 같은 특징들에 대해 서로 다른 차원을 할당
데이터의 특정 variation을 담당하는 latent value를 최대화하여 학습 (Chen et al., 2016)

하지만 이전 연구들은 모두 single modality를 factorize함

MFM은 multimodal representations을 분해하고 생성과 예측에서 modality-specific and multimodal factors의 중요성을 강조함

multimodal data를 latent factor로 분해하는 동시&병렬 작업 (Hsu & Glass 2018)
전체적으로 모델이 다르다!
- prior matching criterion: MFM은 MMD 사용, Hsu는 KL을 사용
- graphical model design: MFM은 single network를 사용, Hsu는 separate networks를 사용
- discriminative objective: MFM은 generative framework에서 라벨을 예측, Hsu는 hinge loss를 추가해서 latent factor를 분리
- MFM은 모든 multimodal fusion encoder와 연결 할 수 있음, Hsu는 early fusion 같은 고정된 multimodal encoder만 사용할 수 있음
- scale of experiments: MFM의 평가 데이터 세트가 훨씬 큼

Multi-Task Learning
1) Multi-Task Learning이란?
서로 연관있는 과제를 동시에 학습함으로써 모든 과제 수행의 성능을 전반적으로 향상시키는 학습 방법
관련 있는 작업들의 표현을 공유함으로써 모델의 일반화 능력을 향상시키는 접근 방식
https://hyoeun-log.tistory.com/entry/WEEK5-Multi-Task-Learning
-> 이 모델 또한 Multi-Task 모델로 봐도 되는지는 모르겠다.

INTRODUCTION

많은 멀티 모달 모델링 task에는 multiple modalities에서 rich representation을 학습하는 문제가 있다.

Multiple modalities는 추가적인 가치있는 정보를 제공하지만,
multimodal data로부터 학습을 할 때 두 가지 challenges가 있다.

모델은 예측을 위해 복잡한 intra-moal과 cross-modal interaction을 학습해야 함
모델은 테스트 중에 예상하지 못한 missing or noisy modalities에 robust해야 함

In this paper,
multimodal data와 label에 걸쳐 joint generative-discriminative objective를 최적화하는 것을 제안한다.

discriminative objective는 학습된 representation이 label을 예측하는데 유용한 intra-modal feature와 cross-modal feature가 풍부함을 보장한다.
반면, generative objective는 모델이 test 동안에 놓친 modalities를 추론하고 noisy가 많은 modalities를 처리할 수 있도록 한다.

이를 위해, Multimodal Factorization Model(MFM)을 소개한다.
-> multimodal representations을 multimodal discriminative factors와 modality-specific generative factors로 분해하는 모델

Notation

${X}_{1:M}$ : multimodal data from M modalities
$\hat {X}_{1:M}$ : generated multimodal data
$Y$ : labels
$\hat Y$ : generated labels
$Z_y$ , $Z_{a\{1:M\}}$ : latent value
multimodal discriminative factor $F_y$
- 모든 modality에 걸쳐 공유
- sentiment prediction과 같은 discriminative tasks에 필요한 joint multimodal features를 포함
modality-specific generative factor $F_{a\{1:M\}}$
- 각 modality별로 unique
- data generating에 필요한 정보를 포함

이 방법은 모든 generative & discriminative information을 요약하는 single factor를 jointly learning 하는 기존 방식과 대조된다.

multimodal discriminative factor는 6개의 멀티모달 데이터 셋에서 SOTA를 달성하였고 (분류)
modality specific generative factors를 사용하면
1) factorized variables를 기반으로 data를 생성하고
2) missing modalities를 설명하며
3) multimodal learning과 관련된 interactions을 더 잘 설명할 수 있음

MULTIMODAL FACTORIZATION MODEL (MFM)

MFM은 multimodal discriminative factors와 modality-specific generative factors에 대한 conditional independence assumptions이 있는 latent variable model이다.

Latent Variable 잠재 변수
데이터에 직접적으로 나타나지 않지만 현재 데이터 분포를 만드는데 영향을 끼치는 변수
데이터의 형태를 결정함
예를 들어 사람 얼굴 이미지를 생성하는 경우, 적절한 잠재 변수는 성별이 될 수 있음
GAN 모델은 임의의 잠재변수로부터 적절한 데이터를 생성해내는 함수를 학습함

1) 이 assumptions에 따라 multimodal data의 joint distribution에 대한 factorization을 제안한다.

2) factorized distribution에 대한 정확한 posterior 추론은 어려울 수 있기 때문에,
multimodal data에 대한 joint-distribution Wasserstein distance을 최소화하는 것을 기반으로 approximate inference algorithm을 제안한다.

Wasserstein distance
두 확률분포간의 거리를 측정하는 지표
두 확률분포의 연관성을 측정하여 그 거리의 기대값이 가장 작을때의 distance

3) 마지막으로, 일반화된 mean-field assumption을 통해 joint-distribution Wasserstein distance를 근사하여 MFM object를 도출한다.

generalized mean field assumption

Notation

${X}_{1:M}$ : multimodal data from M modalities
$Y$ : labels
$P_{x_{1:M},Y} = P(X_{1:M}, Y)$ : joint distribution

$\hat {X}_{1:M}$ : generated multimodal data
$\hat Y$ : generated labels
$P_{\hat{x}_{1:M},\hat{Y}} = P(\hat{X}_{1:M}, \hat{Y})$ : joint distribution

2.1 FACTORIZED MULTIMODAL REPRESENTATIONS

Multimodal discriminative factors와 modality-specific generative factors로 factorize하기 위해 MFM은 Bayesian network structure를 추정한다.

Bayesian network structure
조건부 확률을 사용하여 복잡한 모델 (결합 분포)를 쉽게 표현하기 위해 그래프로 표현하는 방식
conditional independence 가정을 전제로 하며,
random variable들의 full joint distribution을 간단하게 표현함
Directed Acyclic Graph + Conditional Probability Tables

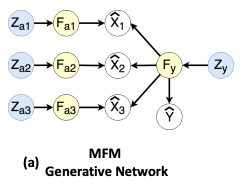
이 graphical model에서
$F_y$ 와 $F_{a\{1:M\}}$ 은 mutually independent(상호 독립적인) latent variables인 prior $P_Z$ 와 $Z=[Z_y,Z_{a\{1:M\}}]$ 에서 생성되었다.

$Z_y$ 는 multimodal discriminative factor인 $F_y$ 를 생성하고
$Z_{a\{1:M\}}$ 는 modality-specific generative factors인 $F_{a\{1:M\}}$ 을 생성함

구조적으로,

$F_y$ 는 $\hat Y$ 에 기여하고
$\{F_y,F_{ai}\}$ 는 $\hat{X}_i$ 의 생성에 기여함

결과적으로,
$P(\hat{X}_{1:M}, \hat{Y})$ 는 다음과 같이 factorize 될 수 있다.

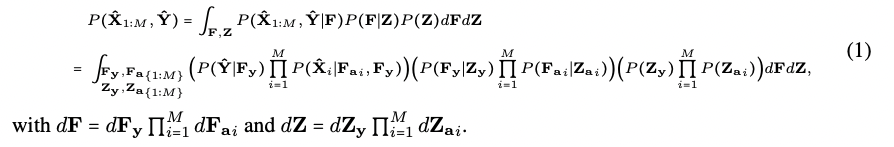
위 식의 정확한 posterior inference는 Z에 대한 integration(통합)으로 인해 분석적으로 다루기 어려울 수 있다.
따라서 다음 section의 approximate inference distribution $Q(Z|X_{1:M}, Y)$ 를 사용한다. (2.2에서 설명.)

MFM은 encoder 모듈 (inference)과 decoder 모듈 (generative)로 구성된 autoencoding 구조로 볼 수 있다.

$Q(⋅∣⋅)$ 의 encoder module을 사용하면 approximate posterior에서 $Z$ 를 쉽게 샘플링할 수 있다.
decoder module은 $P(\hat{X}_{1:M}, \hat{Y}|Z)$ 의 factorization에 따라 매개변수화 된다.

2.2 MINIMIZING JOINT-DISTRIBUTION WASSERSTEIN DISTANCE OVER MULTIMODAL DATA

Autoencoding structures에서 approximate inference의 일반적인 방법 두가지

1) Variational Autoencoders (VAEs)
evidence lower bound objective(ELBO)를 최적화

2) Wasserstein Autoencoders (WAEs)
Wasserstein distance의 primal form(기본 형태)에 대한 approximation를 도출

본 논문에서는 2번을 고려했다.

그러나, WAE는 unimodal data를 위해 설계되었으며 multimodal data를 생성하는 latent variables에 대한 factorized distributions을 고려하지 않았다.
그러므로 이를 위한 변형을 제안함.

encoder와 decoder에서 nonlinear mappings (NN)을 사용했다.

Encoder
$Q_{enc}$ 는 deterministic mapping 학습
- $Q(Z|X_{1:M},Y):X_{1:M},Y->Z$
Decoder: generation process from latent variables
$G_y, G_{a\{1:M\}}, D, F_{1:M}$ 은 neural networks에 의해 deterministic functions parametrized
- $G_y:Z_y->F_y$
- $G_{a\{1:M\}}:Z_{a\{1:M\}}->F_{a\{1:M\}}$
- $D:F_y -> \hat Y$
- $F_{1:M}: F_y,F_{a\{1:M\}}->\hat{X}_{1:M}$

$W_c(P_{X_{1:M}},_Y,P_{\hat X_{1:M}},_{\hat Y})$ 가 cost function $c_{Xi}$ 와 $c_Y$ 에서 multimodal data에 대한
joint-distribution Wasserstein distance를 나타내도록 하자.

식 (1)에서의 conditional independence assumptions를 사용해서 다음과 같이 표현할 수 있다.

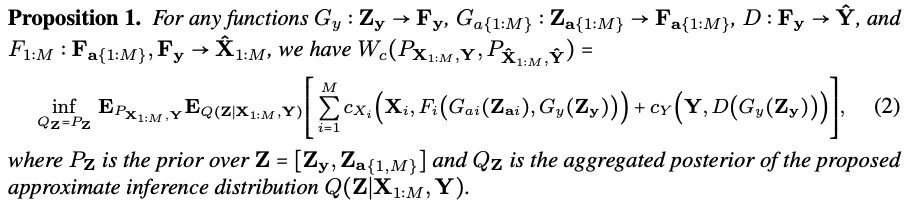
위 식을 정리해서 다시 간단하게 보자면!!

= $c_{X_i}(X_i,\hat X_i)+c_Y(Y,\hat Y)$

squared cost
$c(a,b)=||a-b||_2^2$
-> minimize the 2-Wasserstein distance

static data 뿐만 아니라 time series data(text, audio, video)에서도 정의 가능함

$Q_z = P_z$ 를 만족하기 어려우니까 generalized mean field assumption 수행

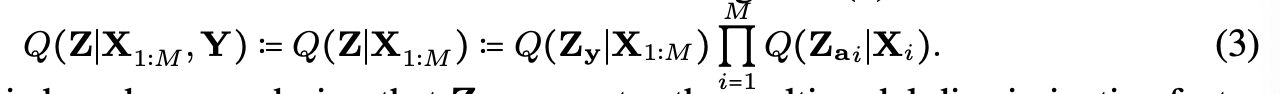
~~-> Y가 왜 없어질까? 모르겠네!~~

본 논문의 design은 다음과 같은 직관을 바탕으로 함

$X_{1:M} -> (추론) -> Z_y -> (생성) -> F_y$
$X_i -> (추론) -> Z_ai -> (생성) -> F_{a\{1:M\}}$

즉, $Z_y$ 가 $F_y$ 를 생성, $Z_y$ 의 추론이 모든 modality $X_{1:M}$ 에 의존
$Z_{a\{1:M\}}$ 가 $F_{a\{1:M\}}$ 를 생성, $Z_ai$ 의 추론은 오직 specific modality $X_i$ 에 의존

이 assumption에 따라, 우리는 Q를 식 (3)의 factorization를 충족하는 모든 encoders의 nonparametric set으로 정의한다.

Hybrid generative-discriminative optimization objective

식 (2)의 $E_{Q(Z|X_{1:M},Y)}$ 에 식 (3)을 적용

First loss term: generative objective

Second term: discriminative objective

penalty term: $λMMD(Q_Z, P_Z)$
- $λ$ : hyper parameter
- $MMD$ : Maximum Mean Discrepancy (= divergence measure between $Q_Z$ & $P_Z$ )
- $P_Z$ : chosen as a centered isotropic Gaussian $N(0,I)$

실제로 train data에 대한 empirical estimates를 사용하여 식 (4)의 expectation을 계산한다.

2.3 SURROGATE INFERENCE FOR MISSING MODALITIES

좋은 멀티모달 모델
1. observed modalities에 따라 조건화 된 missing modality를 추론
2. observed modalities만을 기반으로 예측 수행 가능

이를 만족하기 위해,
MFM의 inference process는 observed modalities가 missing modality를 reconstruct하기 위해 surrogate inference network $\Phi$ 를 사용하여 조정한다.

Generation of missing modality

$\hat {X}_1$ : missing modality

$X_{2:M}$ : observed modalities

식 (5)는 missing modality가 있는 경우 entire modality가 아닌 latent code만 추론하면 된다는 것을 의미한다.

2.4 ENCODER AND DECODER DESIGN

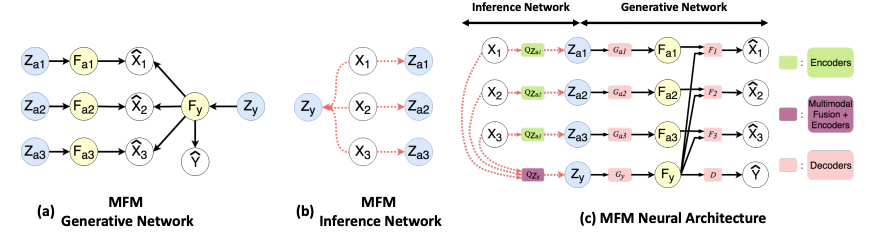
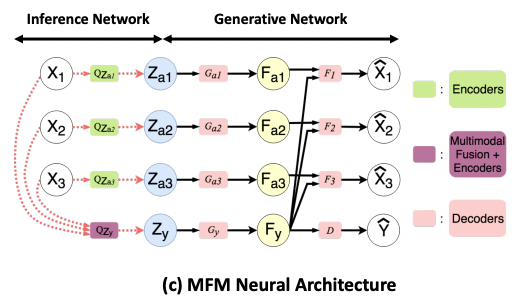
MFM neural architecture in Figure 1(c)

encoder $Q(Z_y∣X_{1∶M})$ : can be parametrized by any model that performs multimodal fusion (보라색)
- multimodal image datasets: CNN & FCNN with late fusion
- multimodal time series datasets: Memory Fusion Network (MFN)
encoder $Q(Z_{a\{1∶M\}}∣X_{1∶M})$ : LSTM network (초록색)
decoder $F_{1:M}$ : decoder LSTM network (분홍색)
decoder $G_y, G_{a\{1:M\}}, D$ : FCNN (분홍색)

https://github.com/pliang279/factorized/

3. EXPERIMENT

1) 기존 baseline과 비교하여 MFM의 discriminative 성능을 평가
2) ablation studies를 통해 각 component의 중요성을 분석
3) missing modalities로부터 modality reconstruction과 prediction 능력을 robustness을 평가
4) information-based와 gradient-based method를 사용하여 learned representations을 해석, 멀티모달 예측 및 생성에 대한 individual factors의 기여도를 이해

3.1 MULTIMODAL SYNTHETIC IMAGE DATASET

synthetic(인조적인) image dataset인 SVHN & MNIST에 대한 분류 및 생성 결과를 확인했다.
SVHN와 MNIST 이미지를 무작위로 쌍으로 구성하여 멀티 모달 데이터 세트를 생성했다.
각 데이터셋을 two modalities로 간주하였다.

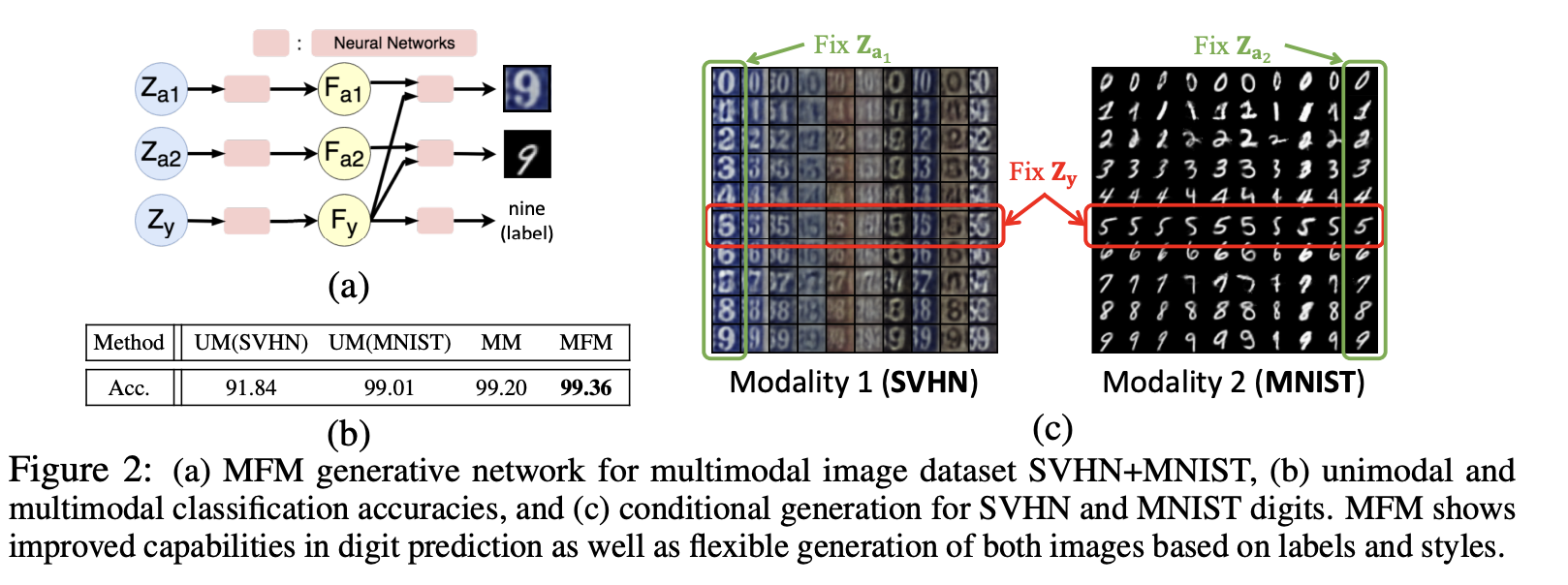
Prediction
1. Unimodal classification task (UM)
2. Multimodal classification task (MM)

더 많은 정보가 주어졌기 때문에 MM에서 UM보다 classification performance가 향상된 것은 당연하다.
다만, MFM이 MM 더 좋은 성능을 내는 것은 discriminative factor 때문이다.

Generation
MFM은 label과 style을 기반으로 두 이미지를 유연하게 생성
이는 MFM이 multimodal representation을 multimodal discriminative factors (labels)와 modality-specific generative factors (styles)로 잘 분해함을 의미

3.2 MULTIMODAL TIME SERIES DATASETS

모든 데이터셋은 monologue video를 포함

Language: GloVe word embedding
Visual: Facet
Acoustic: COVAREP

1) Multimodal Personality Trait Recognition

POM: personality trait이 annotate 된 903개의 영상
confident (con), passionate (pas), voice pleasant (voi), dominant (dom), credible(cre), vivid (viv), expertise (exp), entertaining (ent), reserved (res), trusting (tru), relaxed (rel), outgoing (out), thorough (tho), nervous (ner), persuasive (per) and humorous (hum)

2) Multimodal Sentiment Analysis

CMU-MOSI
ICT-MMMO
YouTube
MOUD

3) Multimodal Emotion Recognition

IEMOCAP

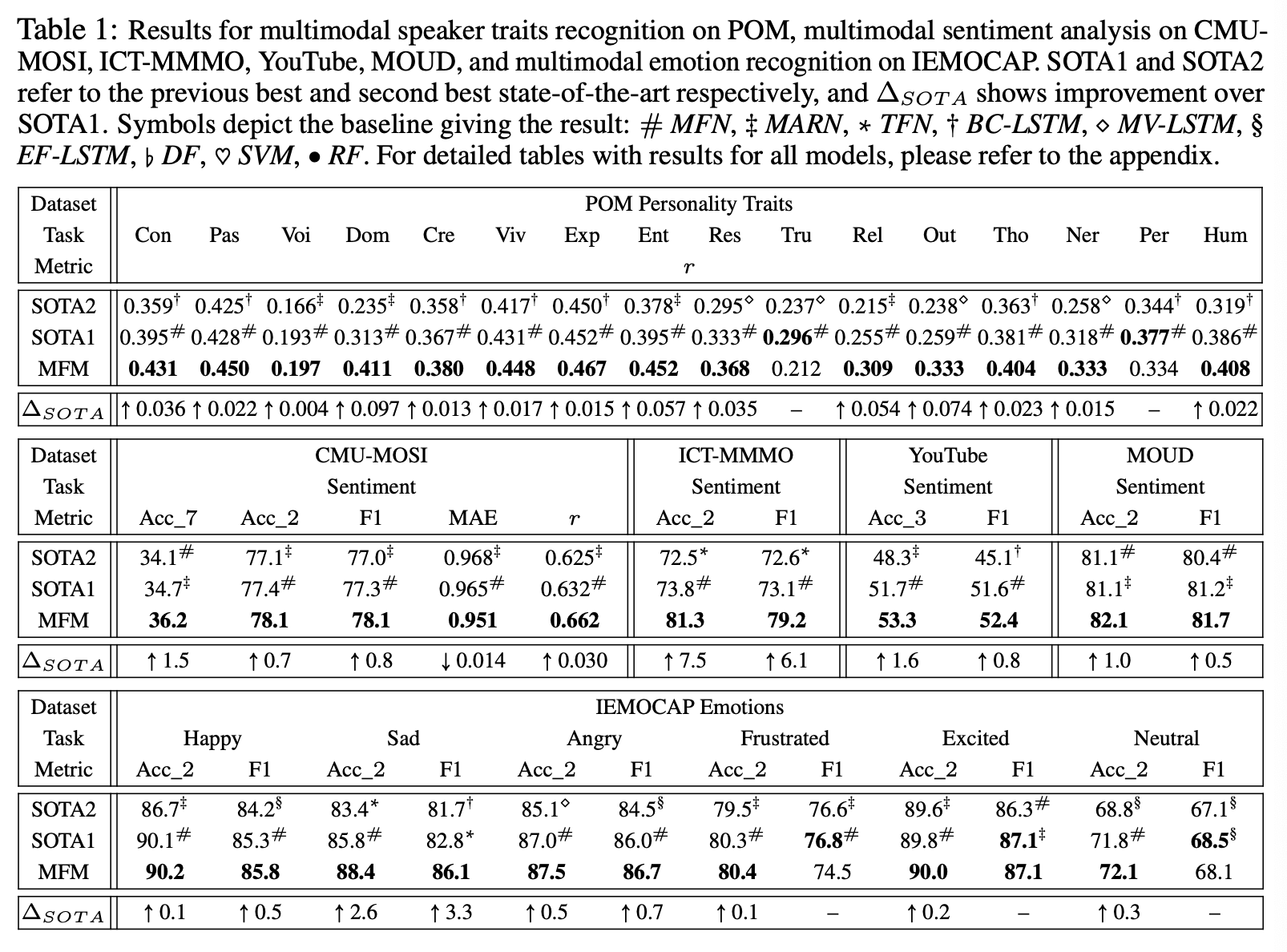
6개의 멀티 모달 데이터 셋에서 SOTA
multimodal discriminative factor $F_y$ 가 discriminative features를 잘 학습함을 알 수 있음
더불어, MFM은 model-agnostic하며 다른 multimodal encoders $Q(Z_y∣X_{1∶M})$ 에 적용할 수 있다.

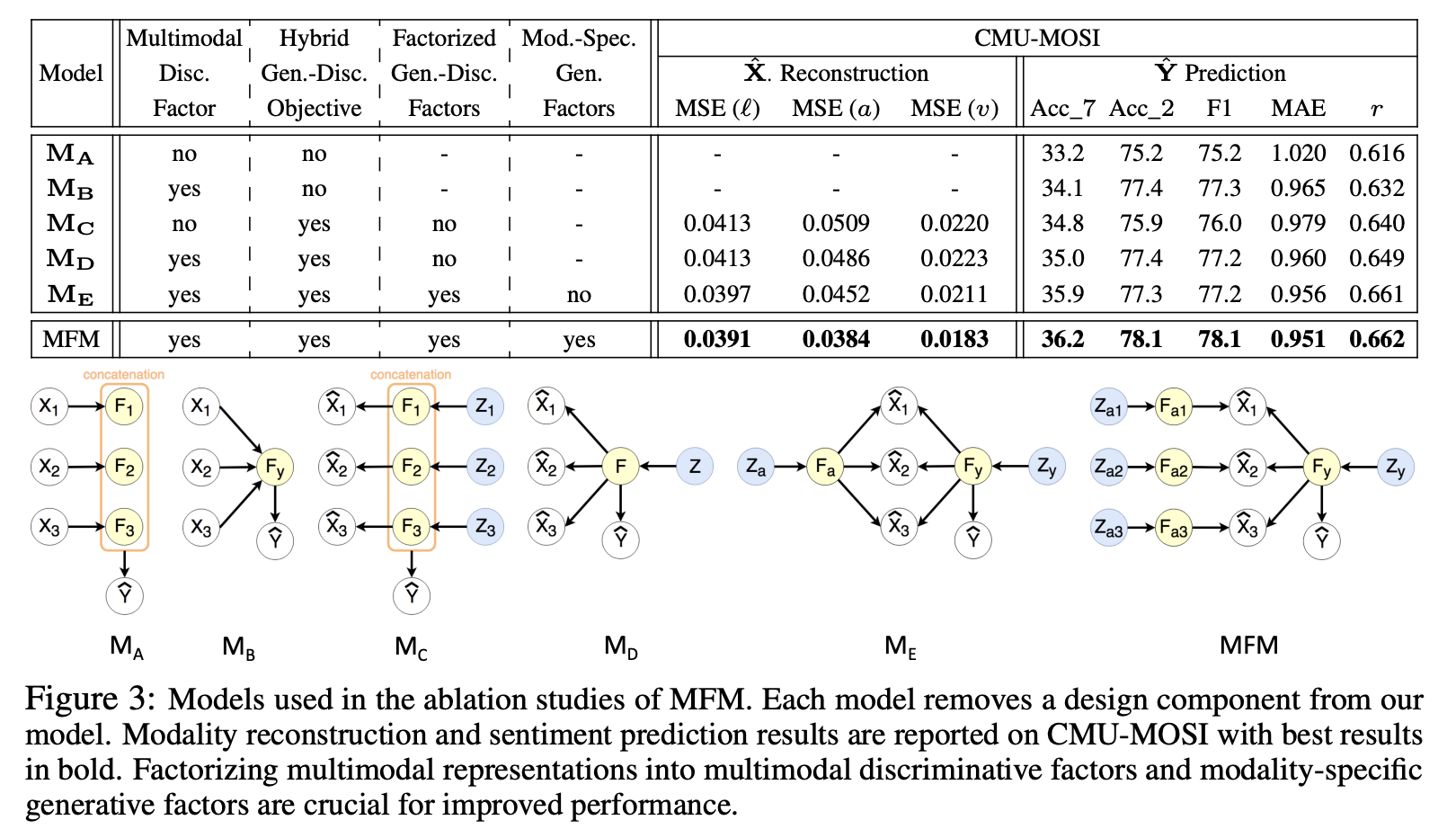
ablation study

네 가지의 effoct를 분석하기 위한 실험

1) multimodal discriminative factor
2) hybrid generative-discriminative objective
3) factorized generative-discriminative factors
4) modality-specificgenerative factors

modality reconstruction와 label prediction을 모두 실험 진행함

sentiment prediction
1) MD > MC, MB > MA
-> multimodal discriminative factor 가 modality-specific discriminative factors 보다 좋은 성능
2) MC > MA, ME > MB
-> 모델에 generative 성능을 추가하면 prediction 성능이 향상

both sentiment prediction and modality reconstruction
1) ME > MD
-> 별도의 generative & discriminative factors로 분해하면 성능 향상
2) MFM > ME
-> modality-specific generative factors를 사용하면 multimodal generative factors보다 성능 향상

즉, multimodal discriminative factors 와 modality-specific generative factors로 분해하는 것이 유의미함

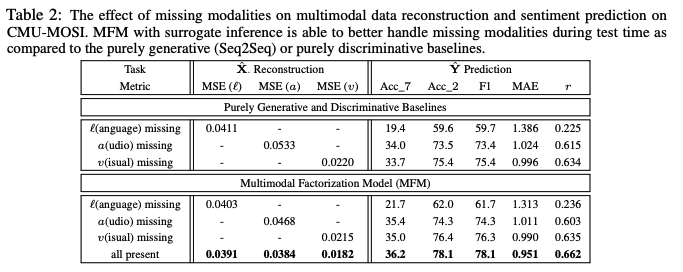
Missing Modalities

2.3의 surrogate inference model을 사용하여 missing modalities가 있는 MFM 성능 평가 진행

두 개의 baseline 비교

1) purely generative Seq2Seq model $\Phi_G$
from observed modalities to missing modalities by optimizing

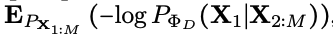
2) purely discriminative model $\Phi_D$
from observed modalities to the label by optimizing

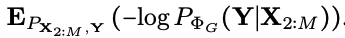
두 모델 모두 두 개의 모달리티만 input으로 사용하도록 MFM을 변형하여 만들었고
sentiment prediction에서 각 모달리티의 reconstruction error를 비교했다.

language가 누락되었을 때 분류 성능이 가장 큰 영향을 받는데, 이는 언어가 인간의 멀티 모달 언어에서 가장 유용하다는 것을 나타내는 이전 연구와 일치한다.
높은 수준의 의미론적 의미를 포함하는 고차원 언어 기능에 비해 낮은 수준의 음향 및 시각적 기능을 재구성하는 것이 더 쉽다는 것을 관찰한다. -> 왜???

Interpretation of Multimodal Representations

MFM의 individual factor가 multimodal prediction과 generation에 영향을 어떻게 주는지를 확인했다.

Method 1) Information-based interpretation method

Multimodal representation에 각 modality가 어떤 contribution을 했는지를 summarize
$F_y$ 가 $\hat X_{1:M}$ 의 common cause이기 때문에 $MI(F_y,\hat X_1), ... , MI(F_y,\hat X_M)$ 을 비교할 수 있다.
이때, $MI(,)$ 는 mutual information measure
가장 큰 $MI(F_y,\hat X_i)$ 가 가장 큰 기여를 함

$r_i = MI(F_y,\hat X_i)/MI(F_{ai},\hat X_i)$

language modality가 가장 sentiment prediction에 가장 많은 기여를 함
이전 연구에서도 입증된 결과임

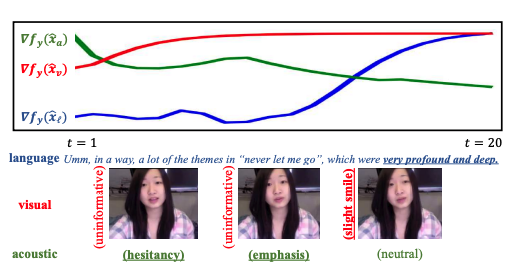
Method 2) Gradient-based interpretation method
Multimodal time series data의 모든 time step에 대한 각 modality의 contribution을 분석
Target factors( $F_y$ )에 대해 생성된 modality의 gradient를 측정

$\{x_1,x_2,...,x_M\}$ : multimodal time series data를 의미
$x_i$ : modality i를 의미함
$\hat{x_i}=[\hat{x_i}^1,\hat{x_i}^2,...,\hat{x_i}^T]$ : time steps $t \in [1,T]$ 동안의 generated modality i

기울기 $∇f_y(\hat x_i)$ 는 인자 $f_y$ ~ $P(F_y|X_{1:M}=x_{1:M})$ 의 변화가 시퀀스 $\hat x_i$ 의 생성에 영향을 미치는 정도를 측정한다

"very profound and deep"이라는 단어와 "hesitant"와 "emphasized"한 tone의 목소리가 $∇f_y$ 의 증가에 영향을 미친다

Conclusion

1) multimodal representation learning을 위한 MFM을 제안

2) MFM은 multimodal representaion을 multimodal discriminative factors와 modality-specific generative factors로 factorize함

3-1) multimodal discriminative factor는 6개의 멀티모달 데이터 셋에서 SOTA 달성

3-2) modality specific generative factors를 사용하면 factorized variables를 기반으로 data를 생성하고 missing modalities를 설명하며 multimodal learning과 관련된 interactions을 더 잘 설명할 수 있음

Future work

Video genration
Semi-supervised learning & Unsupervised learning

Code

mfm_model.py

class MFM(nn.Module):
	def __init__(self,config,NN1Config,NN2Config,gamma1Config,gamma2Config,outConfig):
		super(MFM, self).__init__()
		[self.d_l,self.d_a,self.d_v] = config["input_dims"]
		[self.dh_l,self.dh_a,self.dh_v] = config["h_dims"]
		zy_size = config['zy_size']
		zl_size = config['zl_size']
		za_size = config['za_size']
		zv_size = config['zv_size']
		fy_size = config['fy_size']
		fl_size = config['fl_size']
		fa_size = config['fa_size']
		fv_size = config['fv_size']
		zy_to_fy_dropout = config['zy_to_fy_dropout']
		zl_to_fl_dropout = config['zl_to_fl_dropout']
		za_to_fa_dropout = config['za_to_fa_dropout']
		zv_to_fv_dropout = config['zv_to_fv_dropout']
		fy_to_y_dropout = config['fy_to_y_dropout']
		total_h_dim = self.dh_l+self.dh_a+self.dh_v
		last_mfn_size = total_h_dim + config["memsize"]
		output_dim = config['output_dim']

		self.encoder_l = encoderLSTM(self.d_l,zl_size)
		self.encoder_a = encoderLSTM(self.d_a,za_size)
		self.encoder_v = encoderLSTM(self.d_v,zv_size)

		self.decoder_l = decoderLSTM(fy_size+fl_size,self.d_l)
		self.decoder_a = decoderLSTM(fy_size+fa_size,self.d_a)
		self.decoder_v = decoderLSTM(fy_size+fv_size,self.d_v)
		
		self.mfn_encoder = MFN(config,NN1Config,NN2Config,gamma1Config,gamma2Config,outConfig)
		self.last_to_zy_fc1 = nn.Linear(last_mfn_size,zy_size)

		self.zy_to_fy_fc1 = nn.Linear(zy_size,fy_size)
		self.zy_to_fy_fc2 = nn.Linear(fy_size,fy_size)
		self.zy_to_fy_dropout = nn.Dropout(zy_to_fy_dropout)

		self.zl_to_fl_fc1 = nn.Linear(zl_size,fl_size)
		self.zl_to_fl_fc2 = nn.Linear(fl_size,fl_size)
		self.zl_to_fl_dropout = nn.Dropout(zl_to_fl_dropout)

		self.za_to_fa_fc1 = nn.Linear(za_size,fa_size)
		self.za_to_fa_fc2 = nn.Linear(fa_size,fa_size)
		self.za_to_fa_dropout = nn.Dropout(za_to_fa_dropout)

		self.zv_to_fv_fc1 = nn.Linear(zv_size,fv_size)
		self.zv_to_fv_fc2 = nn.Linear(fv_size,fv_size)
		self.zv_to_fv_dropout = nn.Dropout(zv_to_fv_dropout)

		self.fy_to_y_fc1 = nn.Linear(fy_size,fy_size)
		self.fy_to_y_fc2 = nn.Linear(fy_size,output_dim)
		self.fy_to_y_dropout = nn.Dropout(fy_to_y_dropout)

	def forward(self,x):
		x_l = x[:,:,:self.d_l]
		x_a = x[:,:,self.d_l:self.d_l+self.d_a]
		x_v = x[:,:,self.d_l+self.d_a:]
		# x is t x n x d
		n = x.shape[1]
		t = x.shape[0]

		zl = self.encoder_l.forward(x_l)
		za = self.encoder_a.forward(x_a)
		zv = self.encoder_v.forward(x_v)

		mfn_last = self.mfn_encoder.forward(x)
		zy = self.last_to_zy_fc1(mfn_last)
		mmd_loss = loss_MMD(zl)+loss_MMD(za)+loss_MMD(zv)+loss_MMD(zy)
		missing_loss = 0.0

		fy = F.relu(self.zy_to_fy_fc2(self.zy_to_fy_dropout(F.relu(self.zy_to_fy_fc1(zy)))))
		fl = F.relu(self.zl_to_fl_fc2(self.zl_to_fl_dropout(F.relu(self.zl_to_fl_fc1(zl)))))
		fa = F.relu(self.za_to_fa_fc2(self.za_to_fa_dropout(F.relu(self.za_to_fa_fc1(za)))))
		fv = F.relu(self.zv_to_fv_fc2(self.zv_to_fv_dropout(F.relu(self.zv_to_fv_fc1(zv)))))
		
		fyfl = torch.cat([fy,fl], dim=1)
		fyfa = torch.cat([fy,fa], dim=1)
		fyfv = torch.cat([fy,fv], dim=1)

		dec_len = t
		x_l_hat = self.decoder_l.forward(fyfl,dec_len)
		x_a_hat = self.decoder_a.forward(fyfa,dec_len)
		x_v_hat = self.decoder_v.forward(fyfv,dec_len)
		y_hat = self.fy_to_y_fc2(self.fy_to_y_dropout(F.relu(self.fy_to_y_fc1(fy))))
		decoded = [x_l_hat,x_a_hat,x_v_hat,y_hat]

		return decoded,mmd_loss,missing_loss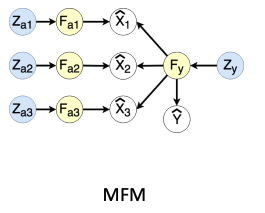

MFM class

나머지 class

MFN (Memory Fusion Network): multimodal time series datasets
MA ~ ME model
MFM missing modality model
seq2seq model
encoder LSTM, decoder LSTM
penalty term의 Maximum Mean Discrepancy 구하는 class
β-VAE에서 사용하는 KL-divergence 구하는 class
kenerl 계산 class

느낀 점

Task에 따라 영향을 주는 요소가 다를 것이라는 가정하에 representation을 잘 학습시키는 모델을 구성한 것이 좋았다.
Modeling 논문들은 수학적 지식들을 야무지게 활용하는데 읽기에는 너무 어렵지만 설득력 측면에서는 역시나 좋은 듯!
다양한 실험들과 Ablation study 창의력 참 좋다~
모델이 비교적 간단해서 그런가 모델 Figure 참 깔끔하게 잘 만들었고 appendix로 헷갈리는 내용 뒤로 다 빼버리고 논문 구성이 읽기에 편~안~했다.
RELATED WORK가 section 2에 없어서 초반에 논문 내용을 파악하는데 약간의 어려움이 있었는데 CONCLUSION 앞에 있었다. 두둥... 근데 다 읽고 나니까 사실 굳이 배경 지식이 필요 없기 때문에 뒤에 넣었다는 생각이 들었다. 매번 논문을 훑어보고 꼼꼼히 볼지, 처음부터 꼼꼼하게 읽을지 고민하다가 후자를 선택했는데, 이번 리뷰를 통해 적어도 목차(논문 구성) 정도는 확인해보고 논문을 읽어야겠다는 생각을 했다.
그래도 앞 부분에서 이게 무슨 소릴까 싶은 것들을 나름 구글링 해가면서 추측(예상)을 하면서 읽었는데 그 추측이 맞았다는 점에서 아주 약간의 뿌듯함이 있었다.
코드 보는 것이 너무 어려워서 큰일이다. 기초적인 쉬운 코드 보는 법부터 다시 익혀야겠다. 진심! 도움 대 환영!

Eun

새해 복 많이 받으세요 ^0^

이전 포스트

[발표용] Learning Factorized Multimodal Representations