스택과 큐
- 스택
- 스택(Stack) 자료구조는 한쪽 끝이 막힌 형태 (ex : 한쪽 끝이 막힌 주차장, 종이컵 수거함 등)
• 입구가 하나이기 때문에 먼저 들어간 것이 가장 나중에 나오는 구조
(선입후출; First In Last Out, 후입선출; Last In Fist Out)
- 큐
- 큐(Queue) 자료구조는 입구와 출구가 따로 있는 원통 형태
• 선입선출; First In Fast Out (FIFO) 구조 (ex. 대기줄)
- 리스트
- 스택과 큐 모두 사용할 수 있음
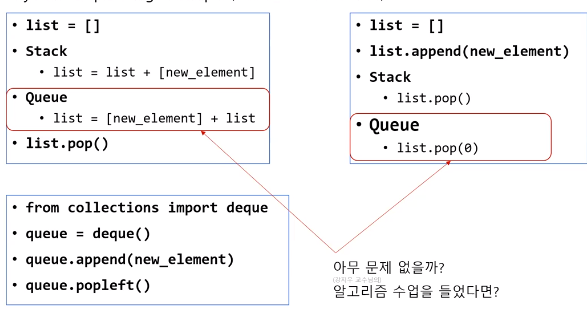
- 파이썬은 Array List 기반
• Linked List가 아니라서 비효율적 / Array List: 한번 넣을 때마다 값을 옮겨야 함
트리
- 이진 트리 (Binary Tree)
• 자식 (Child)노드가 최대 2개 (좌우 노드라고도 함) - 이진 (Binary) 트리의 종류
• 일반 이진 트리
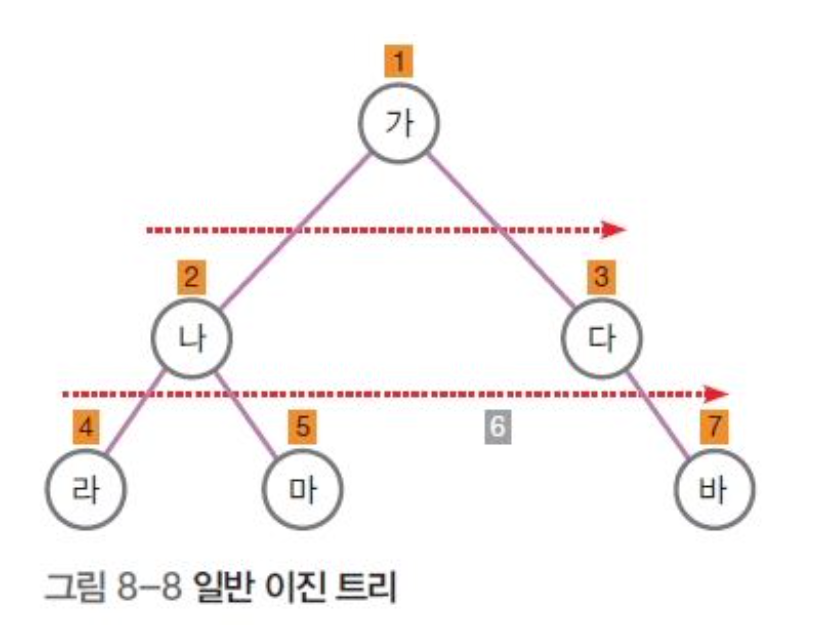
• 포화 (Full), 완전 (Complete) 이진 트리와 와 구분하기 위해서 사용
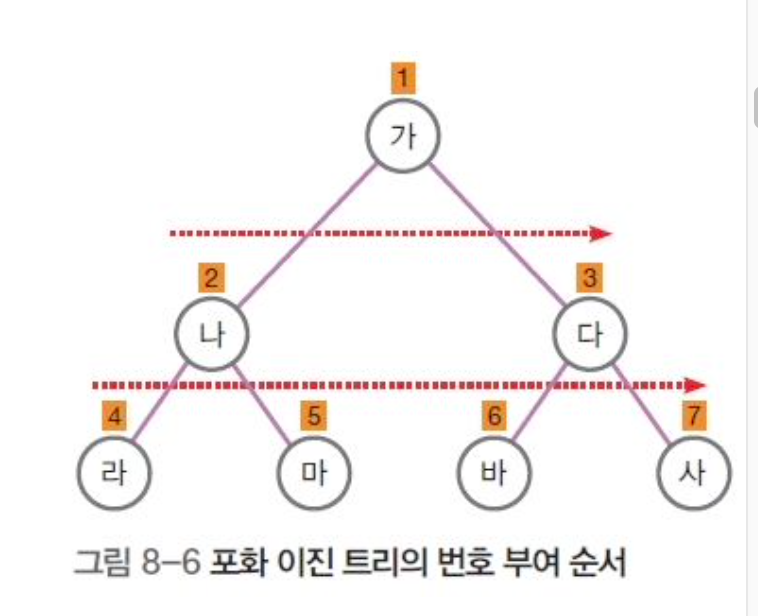
- 포화 이진 트리 (Full Binary Tree)
• 루트로부터 시작해서 모든 노드가 정확히 두 개씩의 자식 노드를 가지도록 꽉 채워진 트리
• 노드수가 2의k승 -1
• 0,1,3,7,15,31
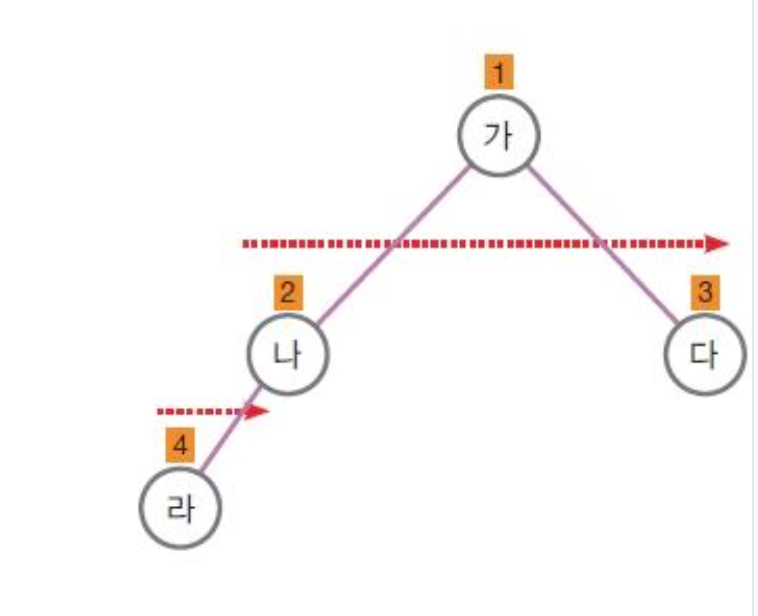
- 완전 이진 트리 (Complete Binary Tree)
• 노드의 수가 맞지 않아 포화이진트리를 만들 수 없을 때 왼쪽부터
모두 채워 나간 이진 트리
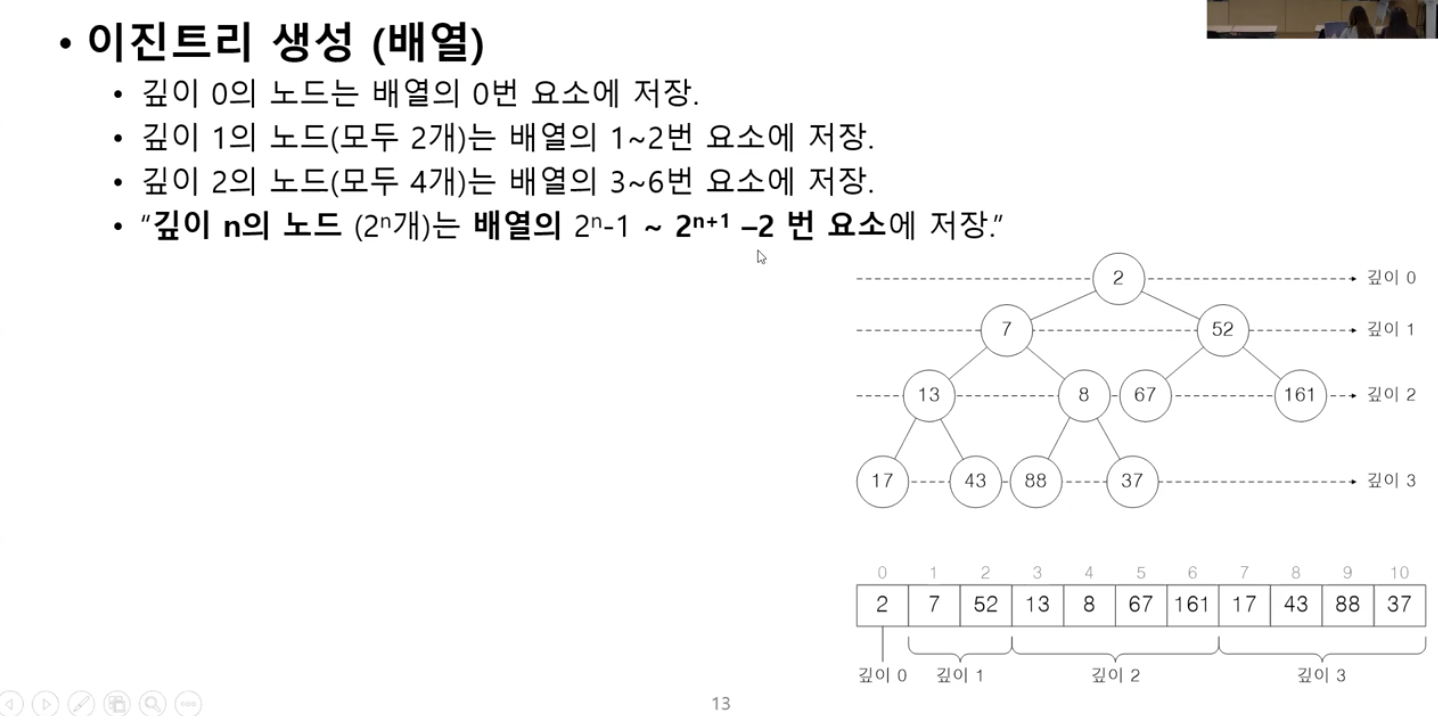
완전이진트리에 가깝다는 가정이 있을 때만 배열로 관리 (메모리가 비어있으면 비효율적이기 때문에)
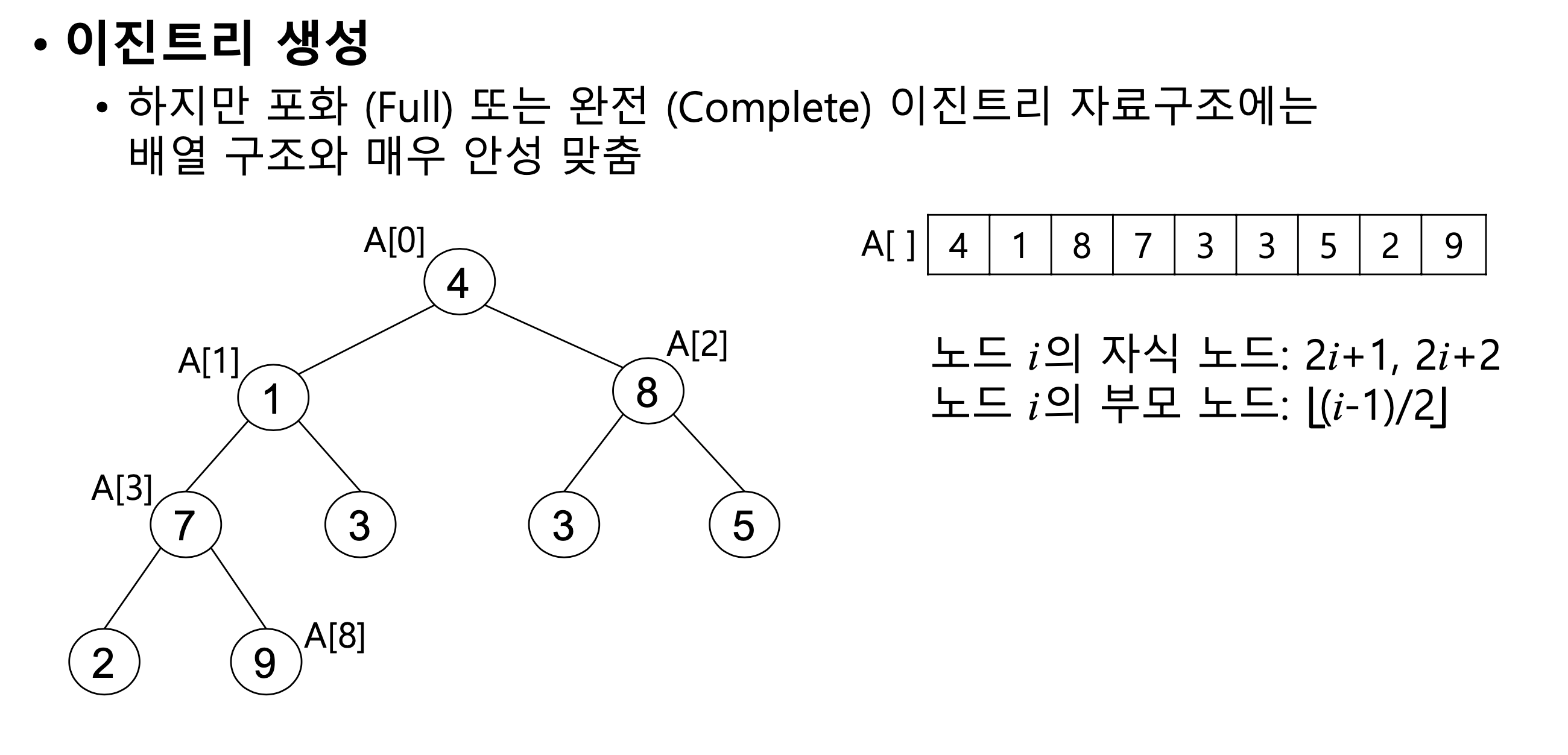
부모노드와 자식노드가 바로 배열 안에서의 인덱싱이 가능하다.
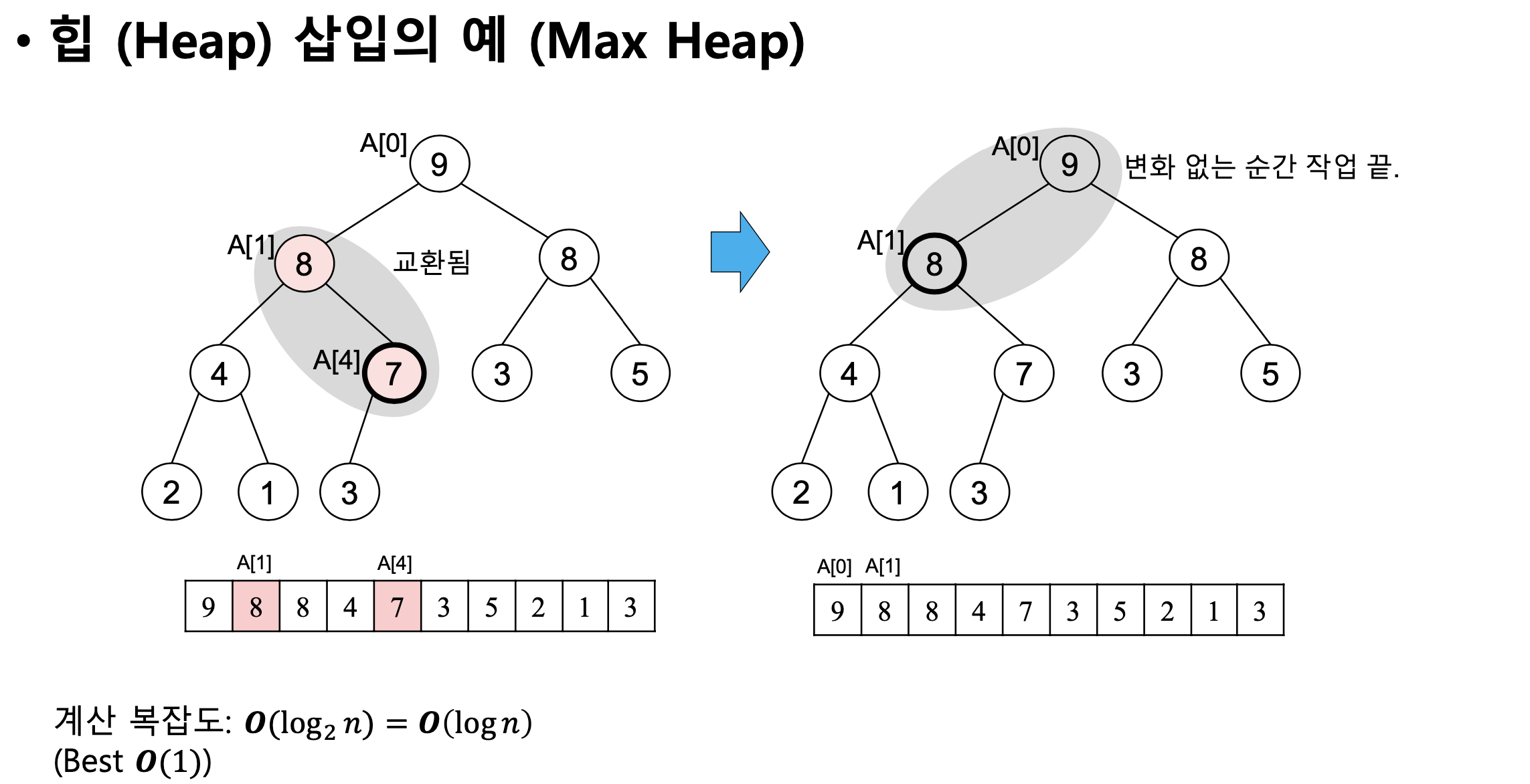
힙(Heap) 자료구조
• 힙 순서 속성 (Heap Order Property)을 만족하는 완전 이진 트리
(Complete Binary Tree)
• 힙 순서 속성 : 트리 내의 모든 노드에 저장된 값은 자식 노드보다 작거나 같아야 한다
• Min Heap (최소힙), Max Heap (최대힙)
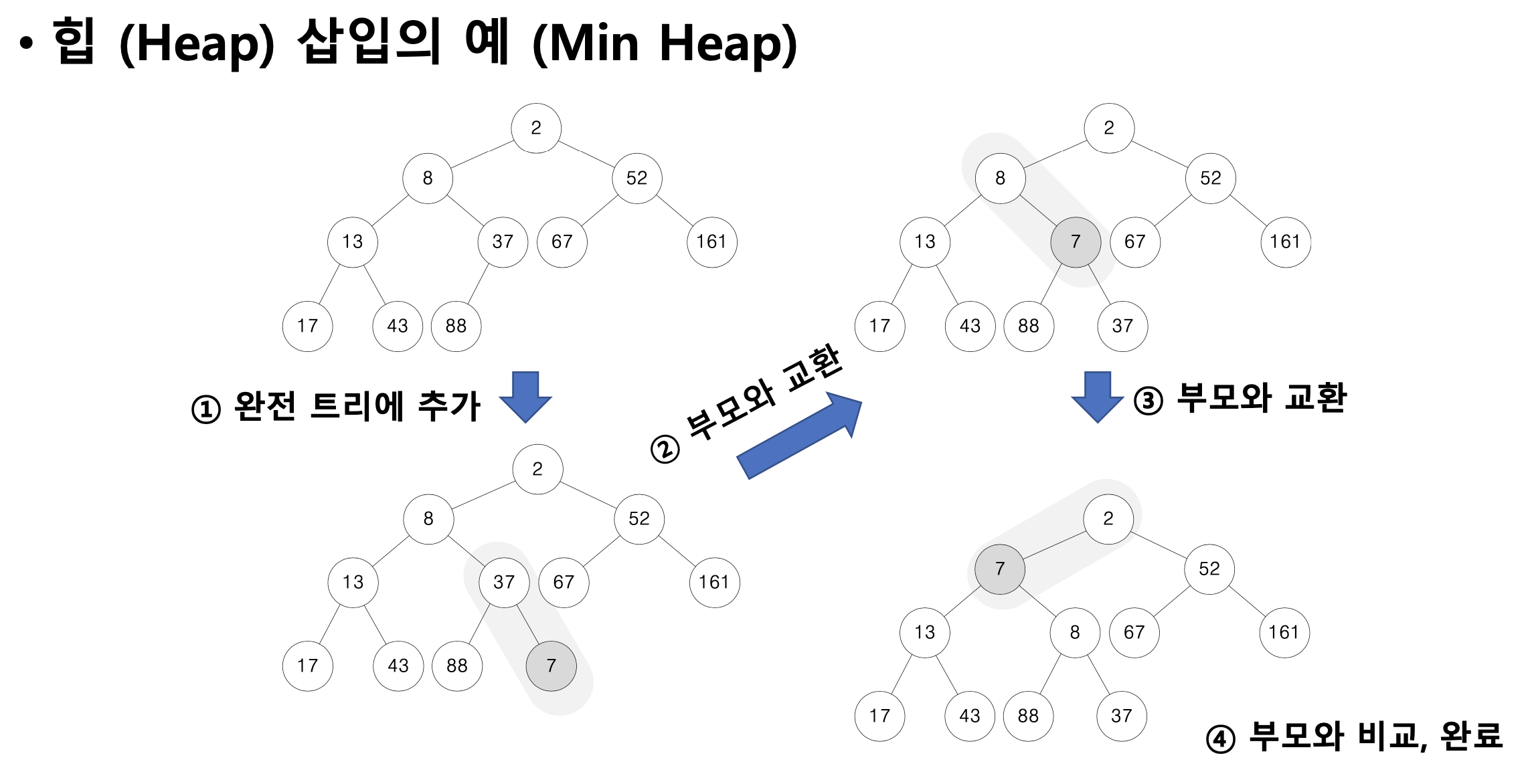
항상 완전이진트리이다.
"힙에서 가장 작은 데이터를 갖는 노드는 루트 노드이다.”를 보장
- max 힙
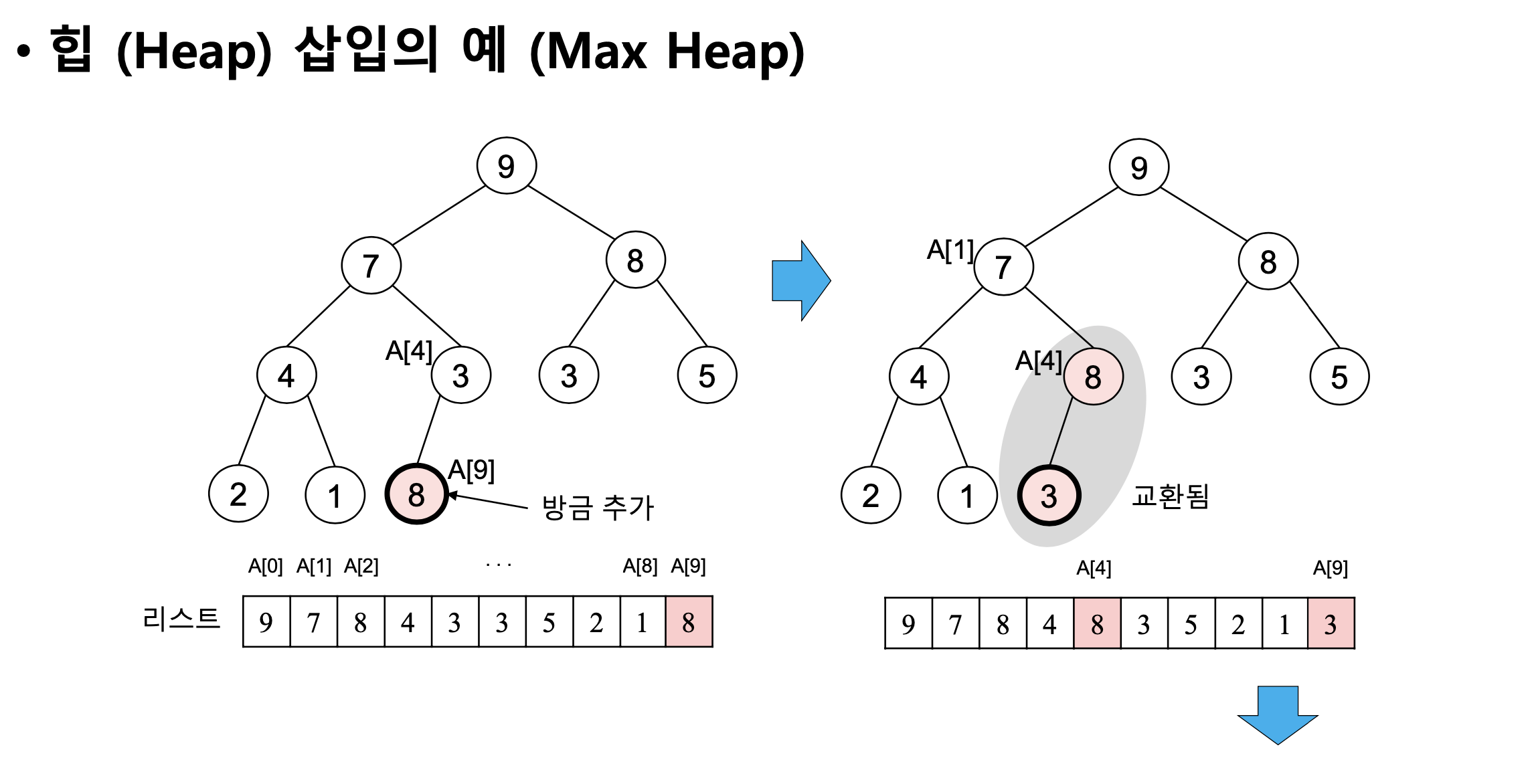
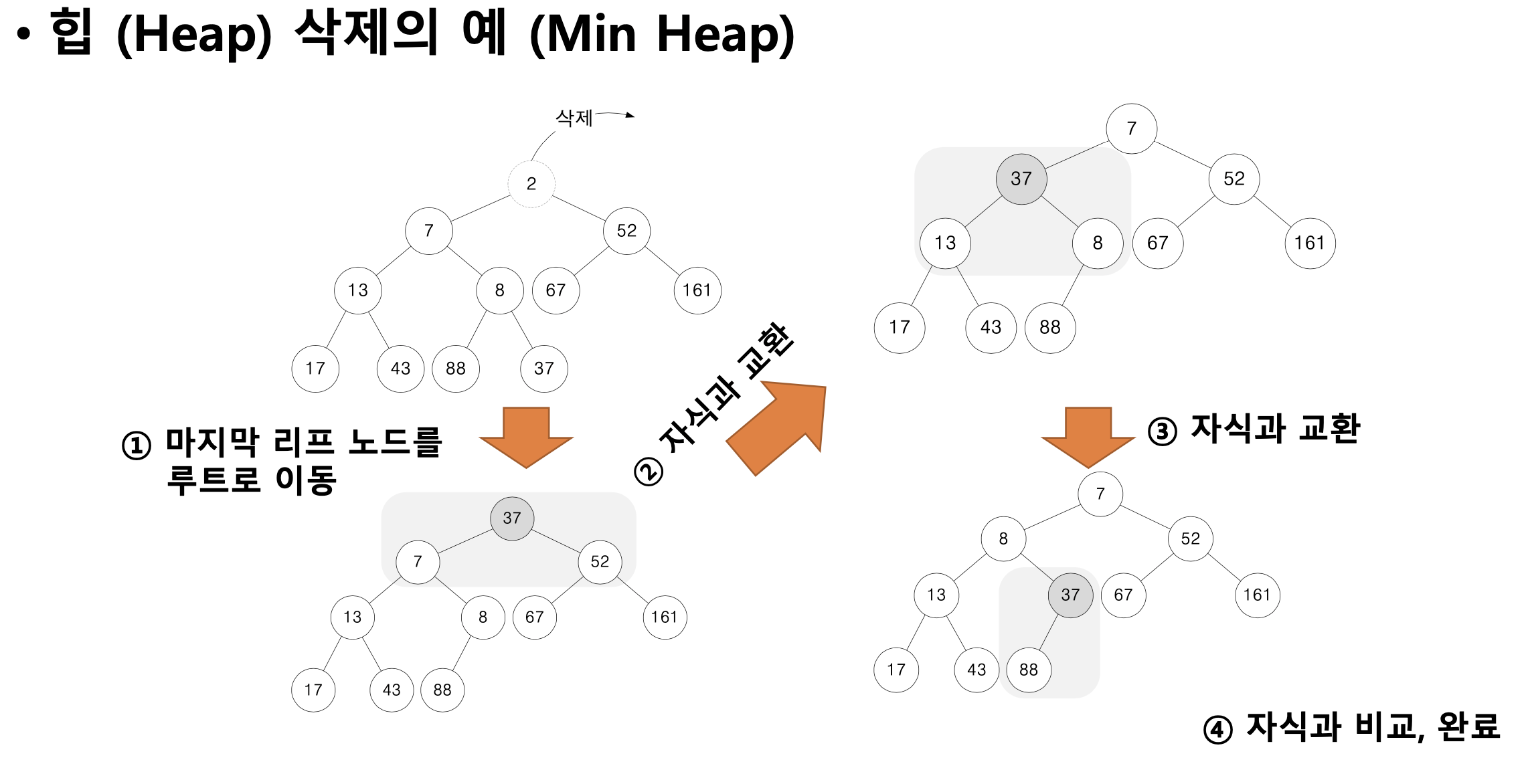
- min 힙 루트 노드 삭제 예시
- 먼저 마지막 리프 노드를 루프로 이동
- 자식과 교환
- 자식과 비교
- max 힙 삭제의 예시
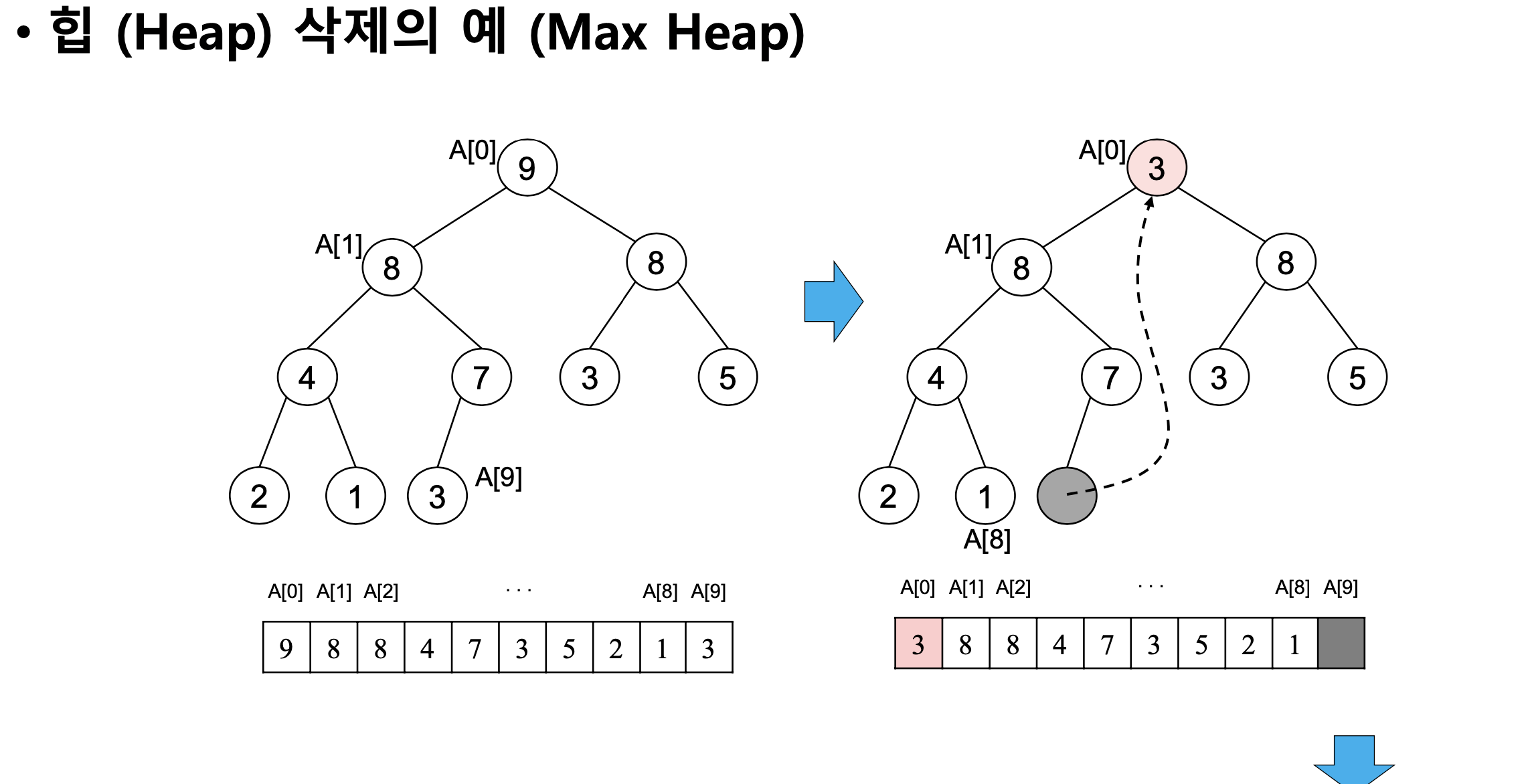
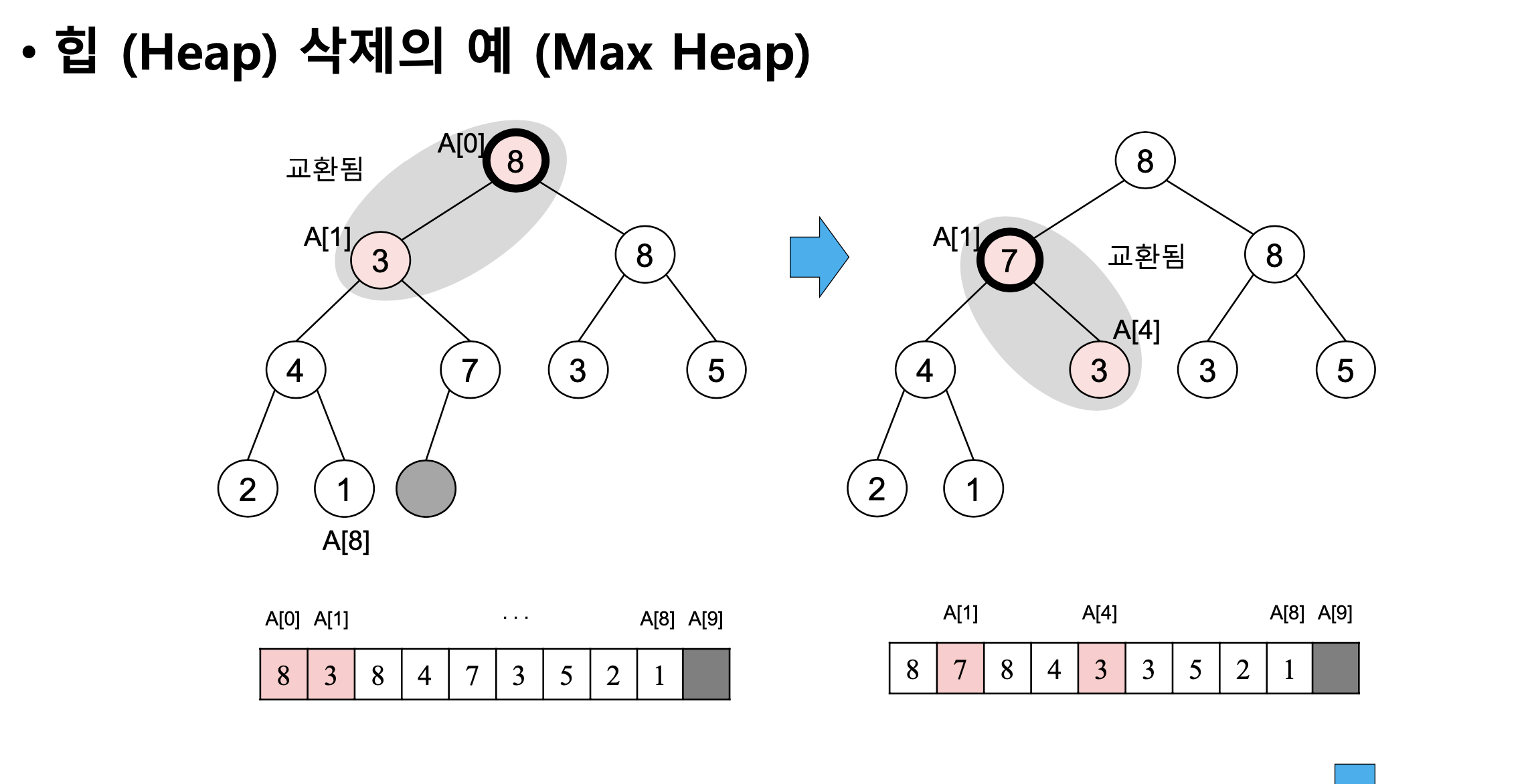
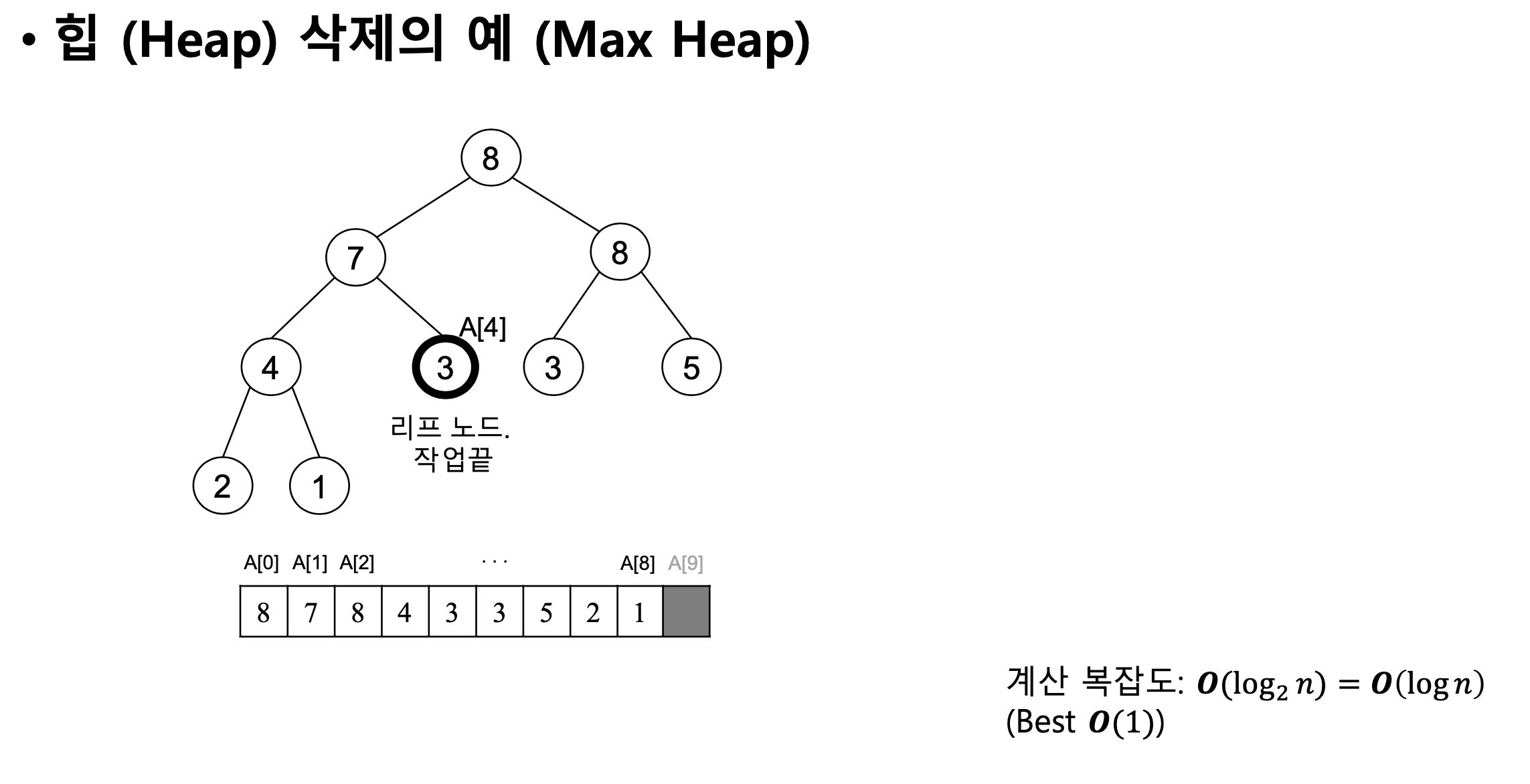
계산 복잡도: log2n
힙 (Heap) 이라는 자료 구조를 왜 쓰는가?
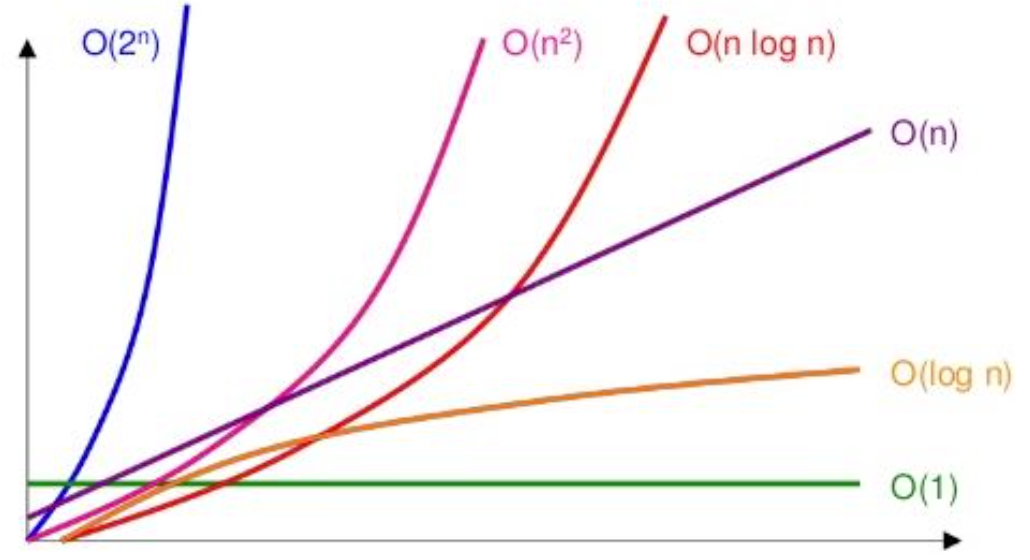
• 정렬된 값의 "삽입"과 "삭제"의 계산 복잡도 비교
배열 (Array) 기반, 연결 리스트 (Linked List) 기반, 힙 (Heap) 기반 리스트
배열 (Array),연결리스트 (Linked List), 힙 (Heap)
삽입: 𝑶(𝑛) 𝑶(𝑛) 𝑶(log 𝑛)
삭제: 𝑶(1) 𝑶(1) 𝑶(log 𝑛)
-
힙을 주로 어디에 쓰는가?
삭제는 크지만 삽입은 더 복잡도가 작다
리스트와 관계 없음 트리 구조를 사용
• 우선순위 큐 (Priority Queue)
• 힙 정렬 (Heap Sort) -
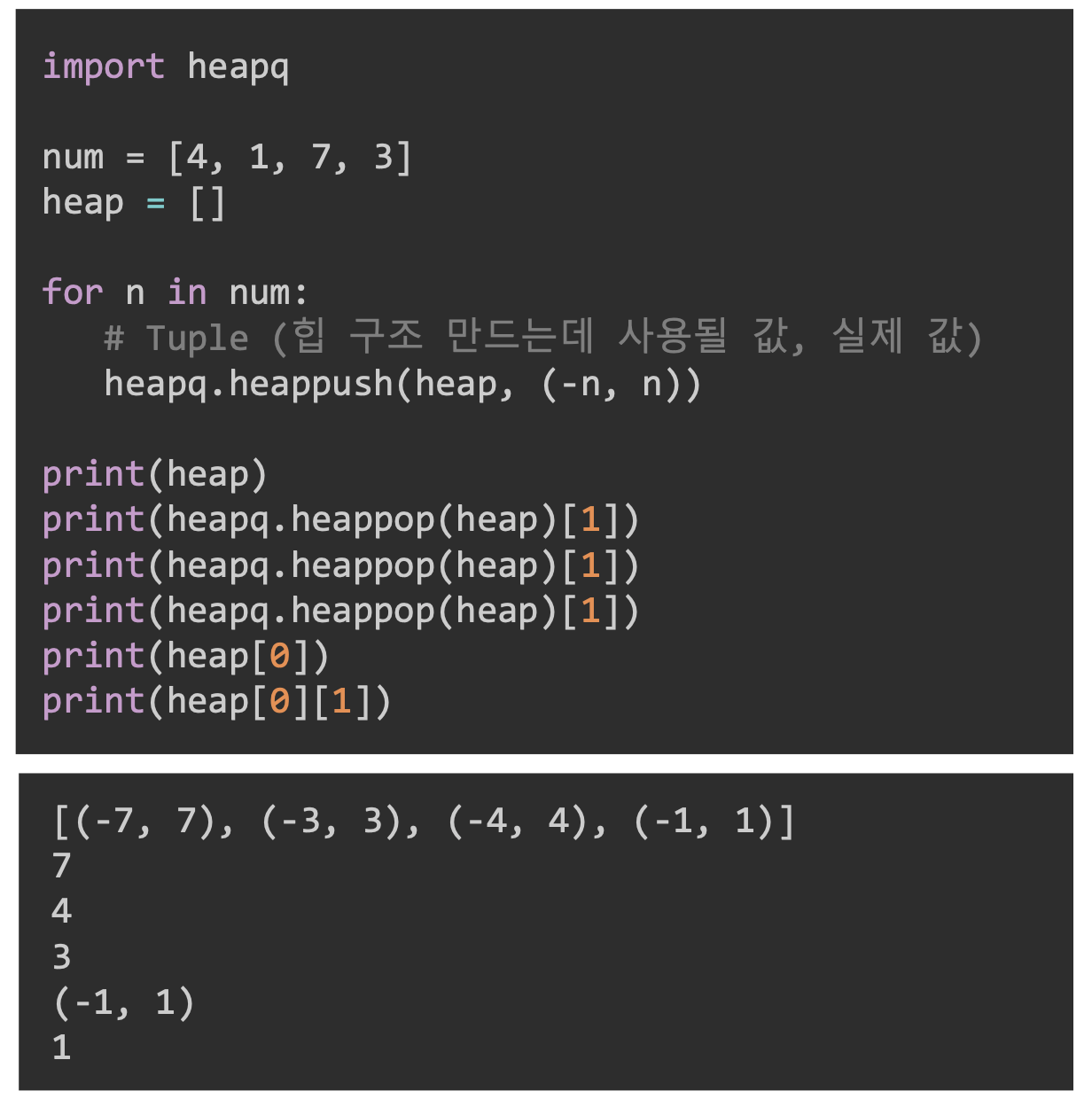
파이썬은 heaq가 있음(힙 자료구조)

heapq는 최소 힙의 구현이기 때문에 최대 힙을 사용하고 싶다면, Python 튜플 (Tuple)과 같은 묶음 자료구조를 사용해서 구현할 수 있다.
(정렬값, 사용값)
• 우선순위 큐 (Priority Queue)
일반적인 큐(Queue)는 먼저 집어넣은 데이터가 먼저 나오는 FIFO (First In First Out) 구조이지만, 우선순위 큐 (Priority Queue)는 들어온 순서와 상관 없이 우선 순위가 높은 데이터 (보통 더 높은 우선순위를 더 낮은 값을 표현) 가 먼저 나옴
힙 정렬 (Merge Sort) Solution
import heapq
def heap_sort(nums):
heap = []
for num in nums:
heapq.heappush(heap, num)
sorted_nums = []
while heap:
sorted_nums.append(heapq.heappop(heap))
return sorted_nums
print(heap_sort([6, 8, 3, 9, 10, 1, 2, 4, 7, 5]))
# 실행결과 : [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
계산 복잡도: 𝑶(𝑛log 𝑛)
best case: 𝑶(𝑛)
추가 자료 참고하기 (힙의 삽입 삭제 과정 코드 사진): 노드 비교 후 교환 등
- heappush도 heapify로 구현 가능 (swap을 아래서 위로 하냐 위에서 아래로 하냐의 차이)
- 파이썬이 heapify를 썼을 때랑 우리가 heapify를 썼을 때랑 값이 다름
(5,7이 위치가 다름 / 내가 움직인 방향만 고려 but 파이썬은 들어오는 애가 코드를 만족하지 않고 있다고 가정: 다 순회하여 검수) >> 순회하도록 고칠 수 있음 - n개의 배열 >> 삽입(heappush)xn번: O(1)이 될 수 있음 >> heap >> 삭제(heapop)xn번: O(1)이 될 수 없음 (7-1 강의 참고)
정렬 (Sort) 그리고 더
• 현존하는 컴퓨터 아키텍처상에서 비교 연산자를 이용하여 구현된 정렬 알고리즘 중 가장 고성능인 알고리즘이 퀵 정렬
• 단 데이터에 접근하는 시간이 오래 걸리는 외부 기억장소 (하드디스크 등)에서 직접 정렬을 수행할 경우에는 병합 정렬이 더 빠른 것으로 알려져 있음
퀵정렬이 왜 힙정렬보다 빠를까
: 캐시메모리에 이유가 있음 바로 옆에 인덱스를 처리
병합정렬 메모리적으로 효율성이 떨어짐
네트워크적으로 멀리 있는 정보를 활용할 때는 퀵 정렬이 좋을 수 있음 (pc 메모리 사용이 비효율적이라 많이 사용되지는 않음)
삽입 정렬: 점근적 / n이 충분히 작을 때는 더 효율적일 수도 있다.
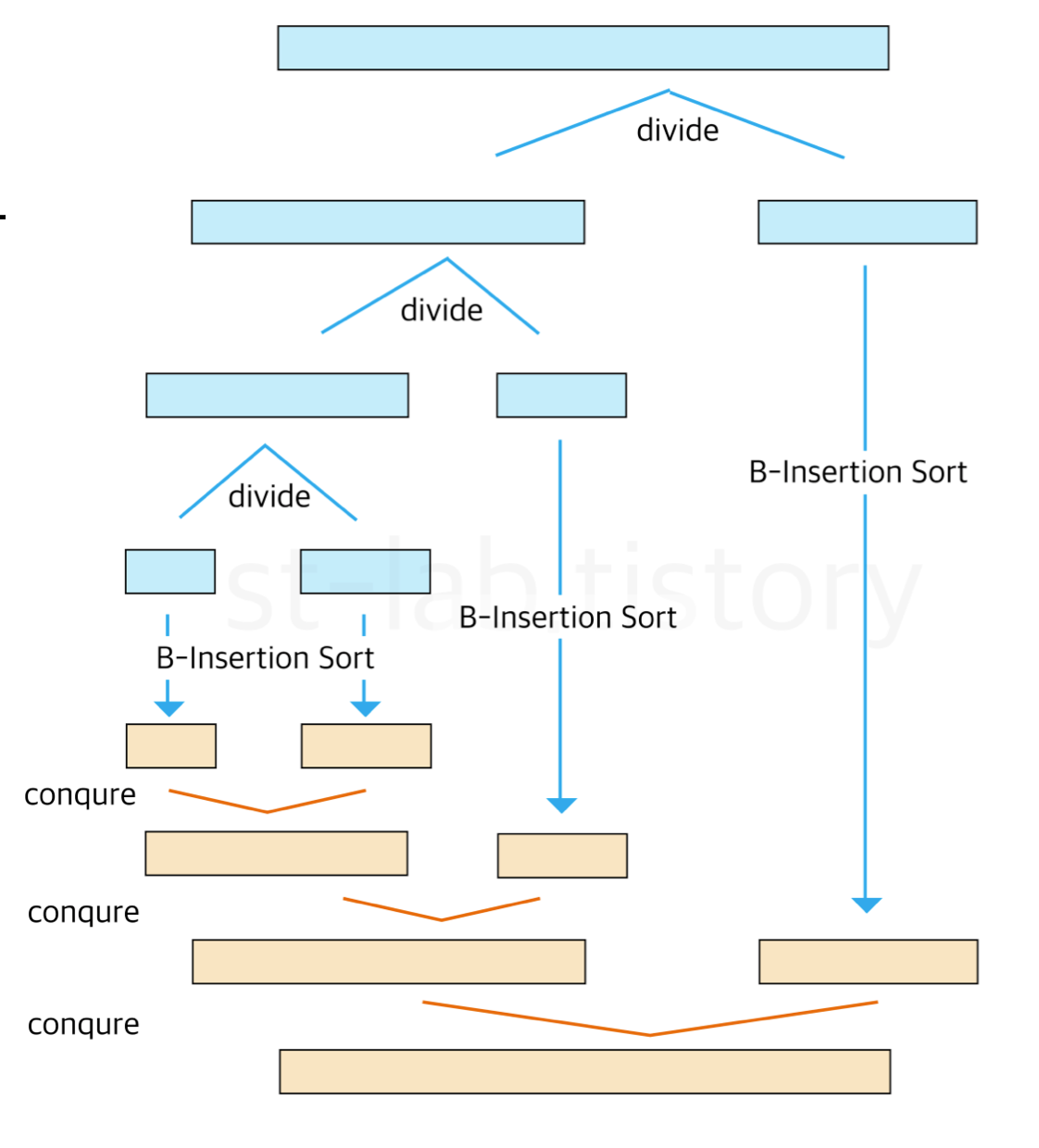
- Binary Insertion (B-Insertion) Sort
• 새로운 원소가 들어갈 위치를 찾는 과정에 이진 탐색 (Binary Search)을 사용
• 그 외는 삽입 정렬과 동일
• Tim Sort(파이썬에서 사용): 기본적으로 삽입 정렬
Tim Peters (2002)
for Python Sort (and > Java 7)
Hybrid Stable Sorting Algorithm • Merge + Insertion Sorts
검색
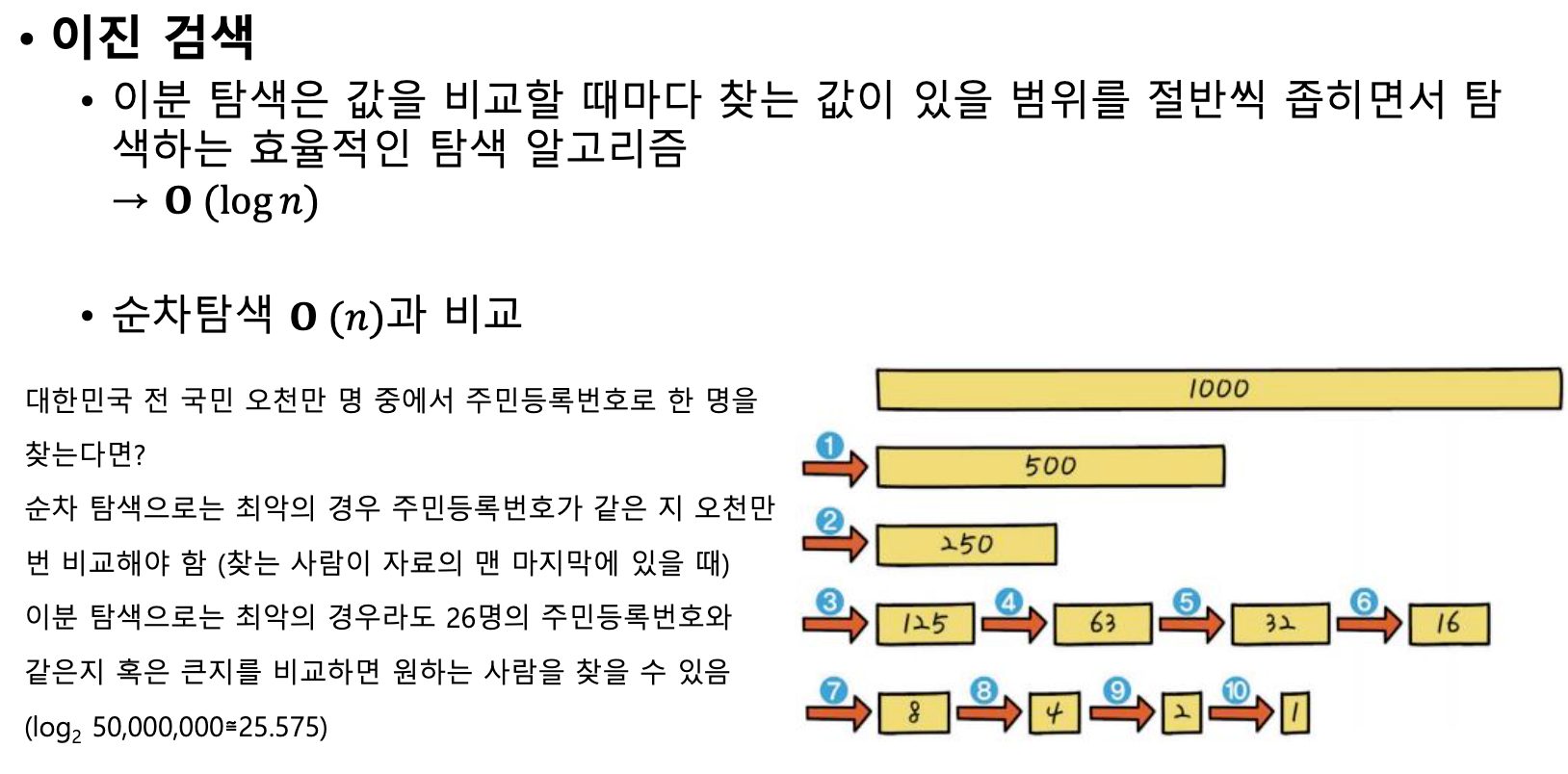
• '검색’은 정렬된 상태에서 더 빠르게 원하는 것을 찾을 수 있음
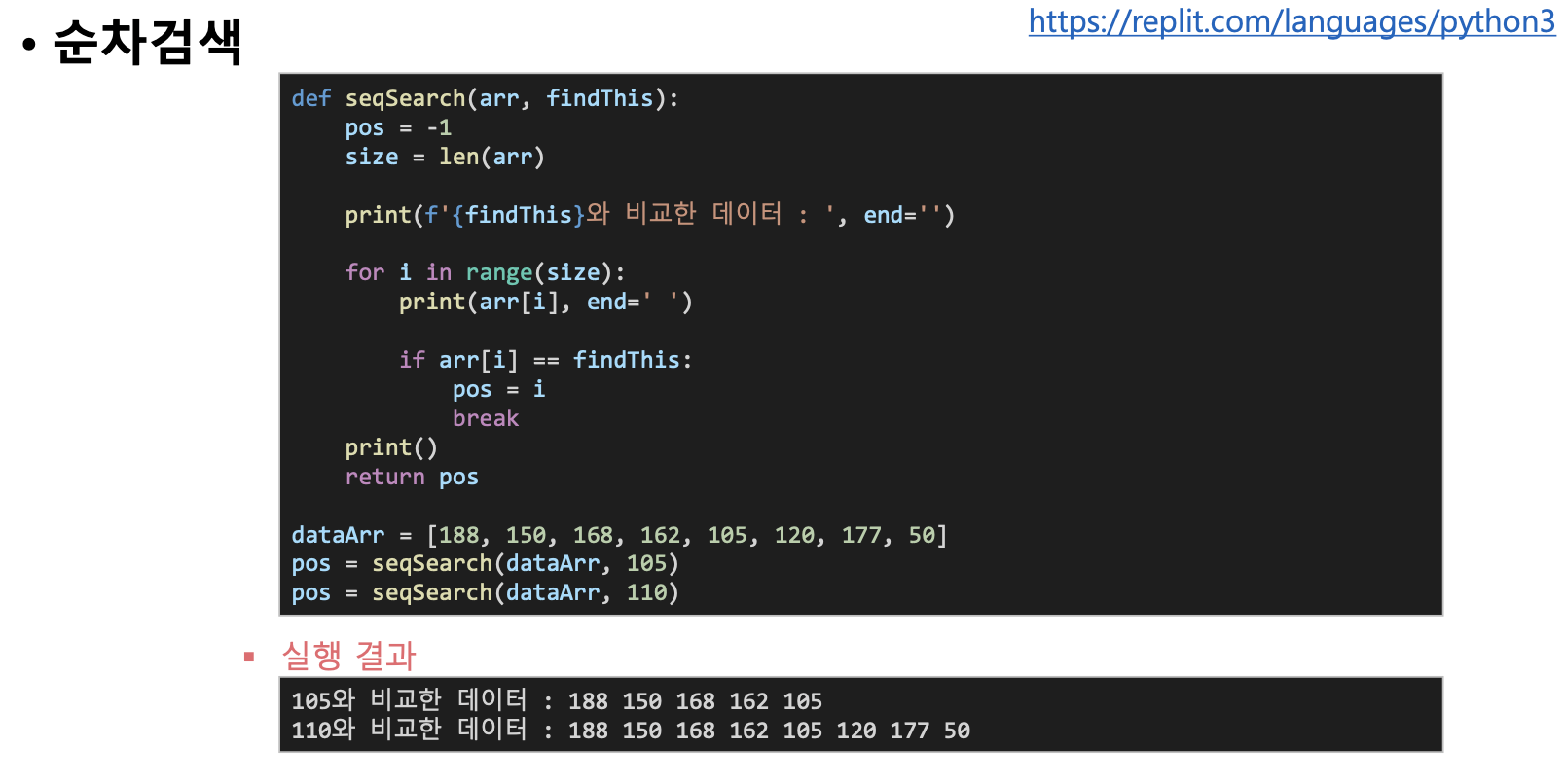
순차 검색
- 검색할 집합이 정렬되어있지 않은 상태일때 처음부터 차례대로 찾아보는 것으로, 쉽지만 비효율적임
- 집합의 데이터가 정렬되어 있지않다면 이 검색 외에 특별한 방법없음
정렬되지 않은 집합의 순차 검색

정렬된 집합의 순차 검색
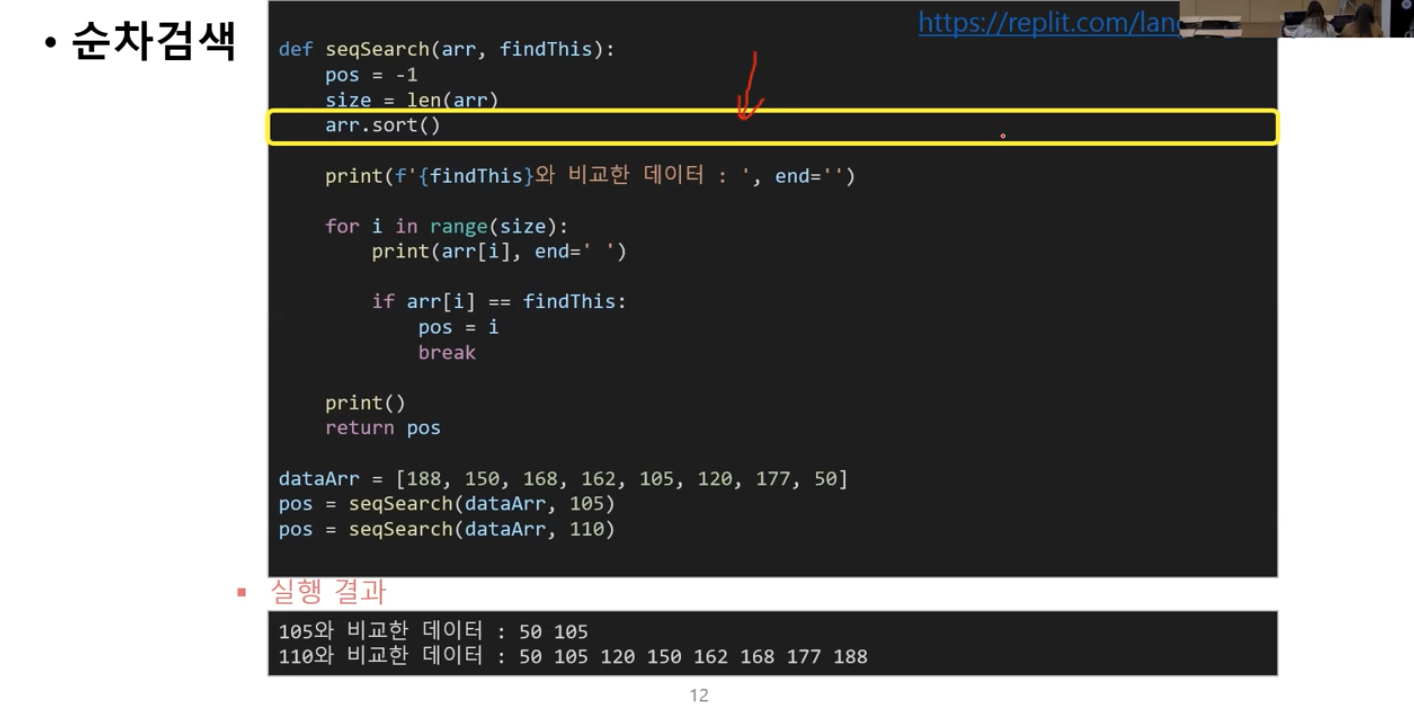
코드 추가되어 짧아짐
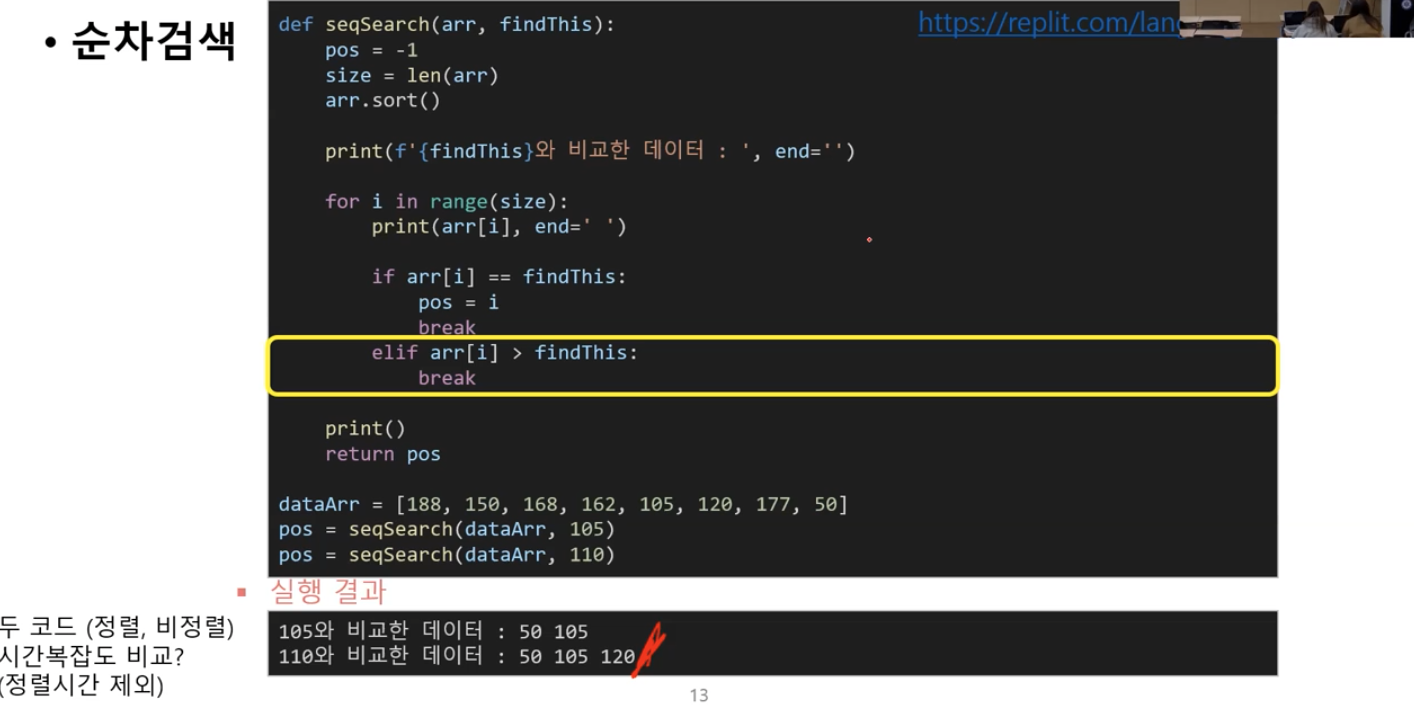
그래봤자 반만 줄었다.(많이 줄지 않았다)
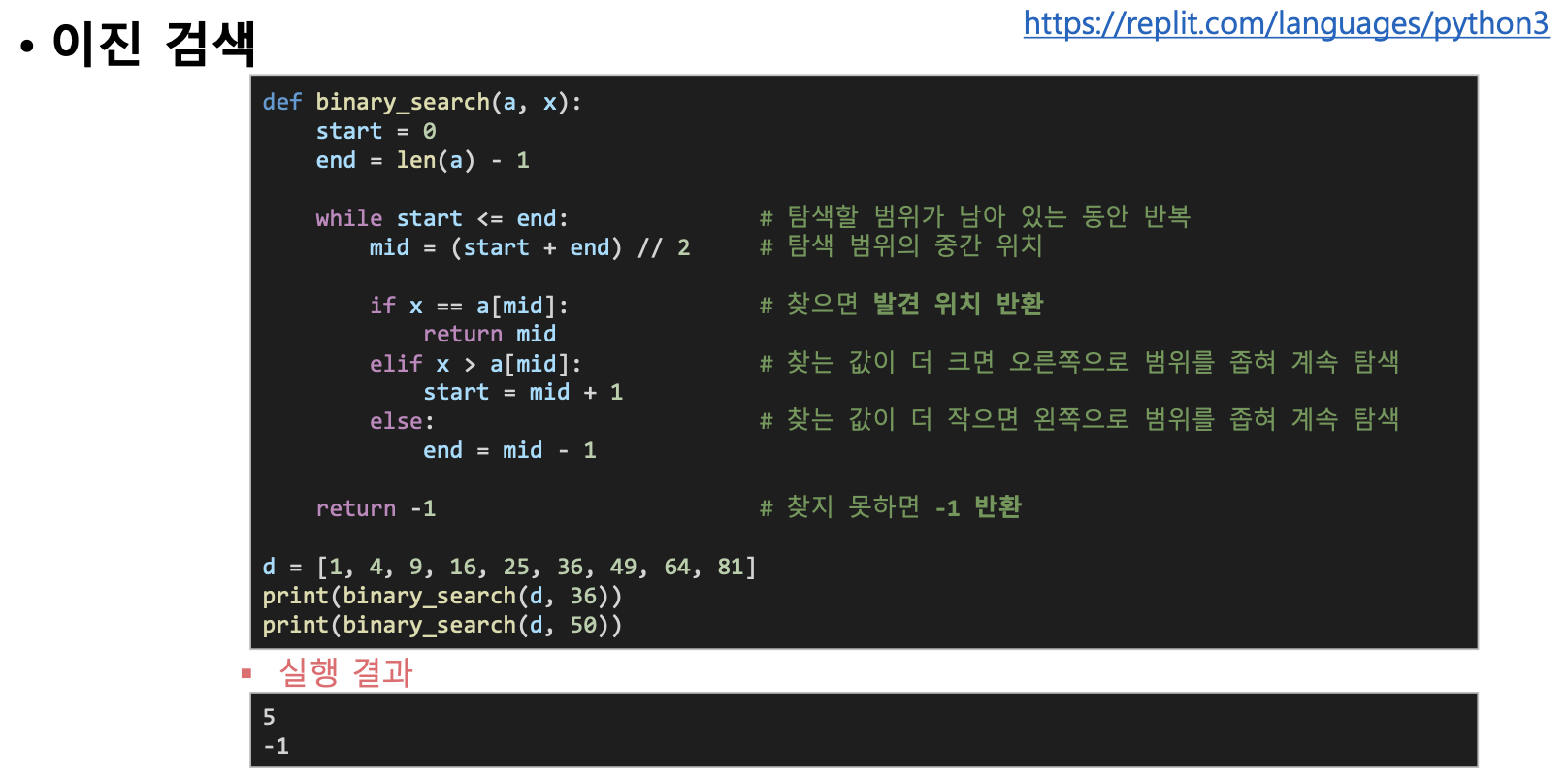
이진 검색
- 데이터가 정렬되어 있다면 이진 검색도 사용 가능
- 순차 검색에 비해 월등히 효율적이라 데이터가 몇천만개 이상이어도 빠르게 찾아 낼 수 있음
- 이진 검색 또는 탐색은 전체를 반씩 잘라서 한쪽을 버리는 방식을 사용
- 𝑶(log 𝑛)
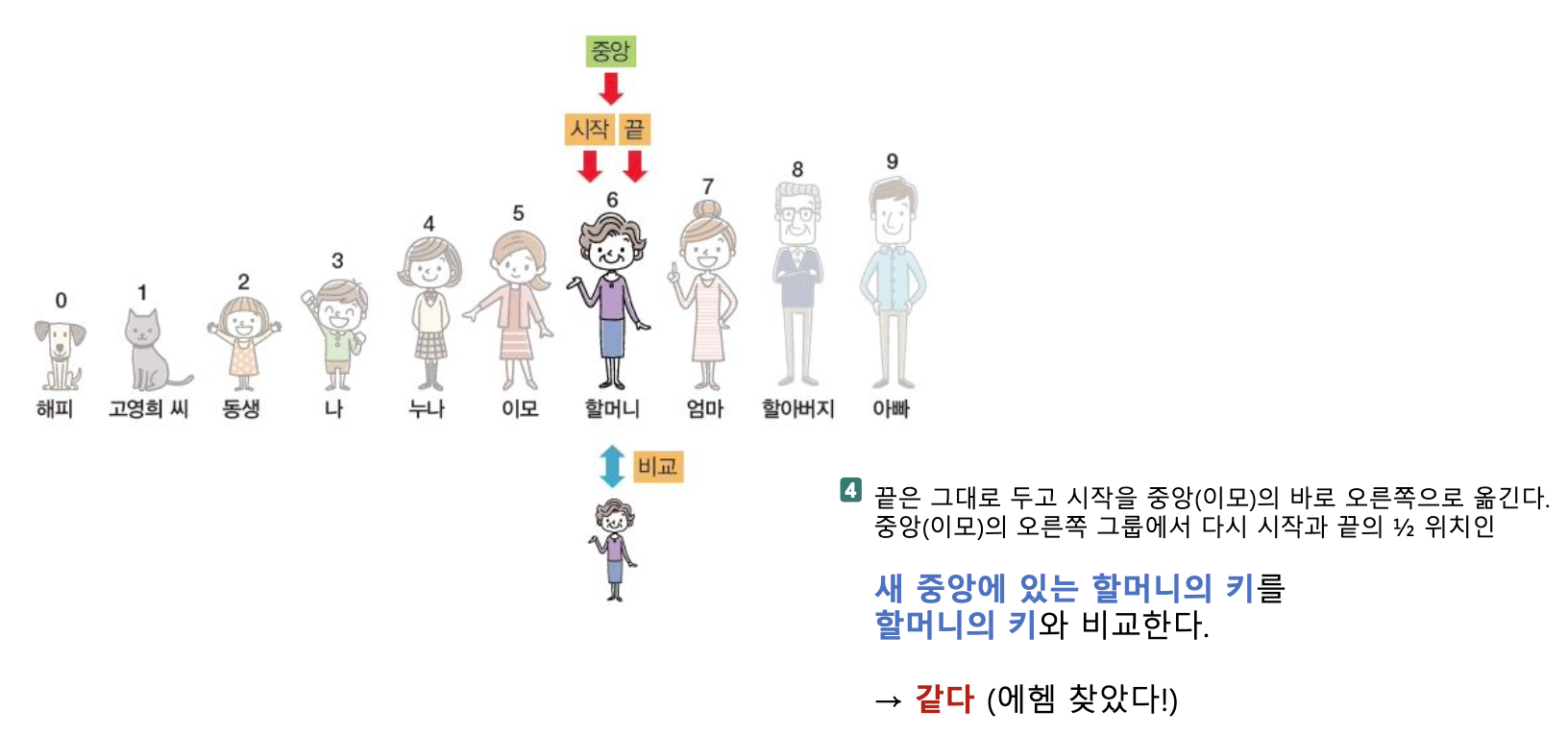
- 전체의 첫 데이터를 '시작'으로 지정하고 마지막 데이터를 '끝'으로 지정한 후 시작과 끝의 중앙에 있는 누나의 키를 (찾고 있는) 할머니의 키와 비교한다.
- 좌측을 버리고 끝은 그대로 두고 시작을 중앙(누나)의 바로 오른쪽으로 옮긴다. 중앙의 오른쪽 그룹에서 다시 시작과 끝의 반절 위치인 새 중앙에 있는 엄마의 키를 할머니의 키와 비교한다.
- 우측은 버리고 시작은 그대로 두고 끝을 중앙(엄마)의 바로 왼쪽(할머니)로 옮긴다. 중앙(엄마)의 왼쪽 그룹에서 다시 시작과 끝의 반절 위치인 새 중앙에 있는 이모의 키를 할머니의 키와 비교한다.
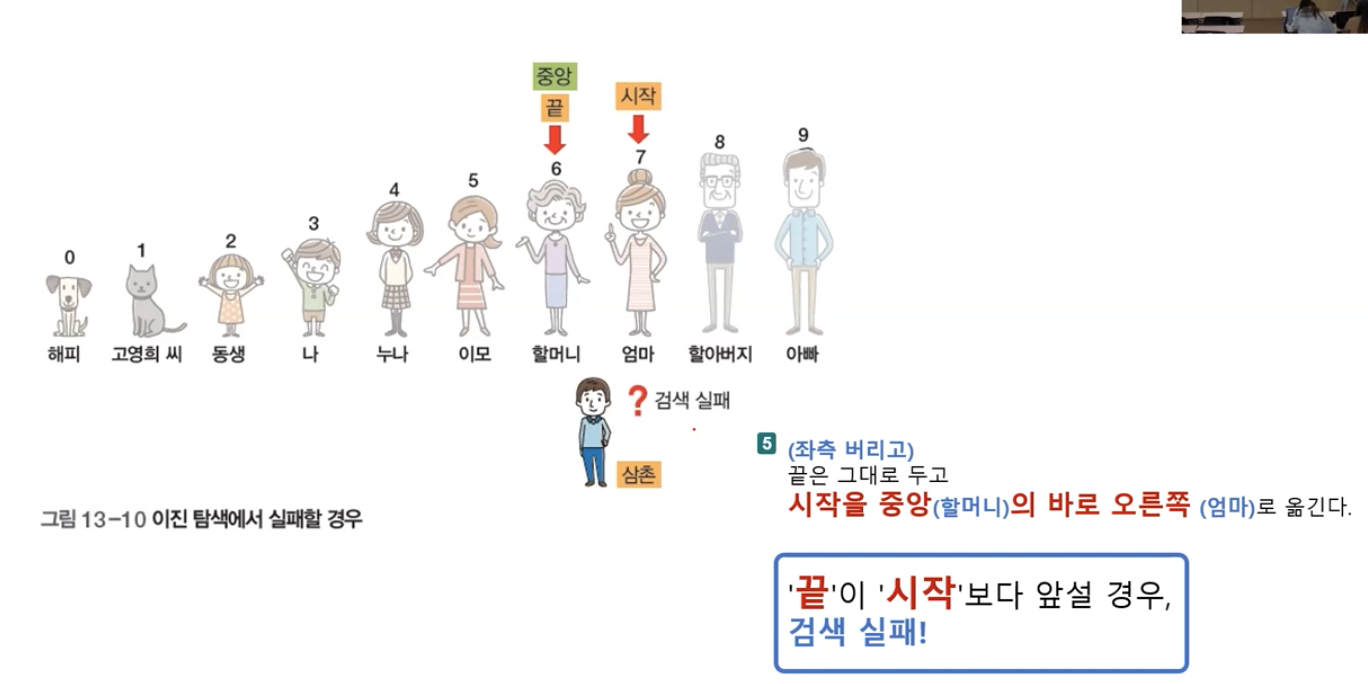
- 할머니보다는 키가 크고, 엄마보다는 키가 작은 삼촌을 찾는다면?
검색실패
▪ 이진 검색 알고리즘 정리
1) 중간 위치를 찾음 → (시작위치 + 끝위치) // 2
2) 찾는 값과 중간 위치 값을 비교
3) 같다면 원하는 값을 찾은 것이므로 위치 번호를 결과값으로 돌려줌
4) 찾는 값이 중간위치 값보다 크다면 중간 위치의 오른쪽을 대상으로 다시 탐색(1번 과정부터 반복) → 시작 위치를 중간 위치 바로 오른쪽으로
5) 찾는 값이 중간위치 값보다 작다면 중간위치의 왼쪽을 대상으로 다시 탐색(1번 과정부터 반복) → 끝 위치를 중간 위치 바로 왼쪽으로
▪ 자료의 중간부터 시작해 찾을 값이 더 크면 오른쪽으로, 작으면 왼쪽으로 점프하며 자료를 찾음
▪ 점프할 때마다 점프 거리는 반씩 줄어듬
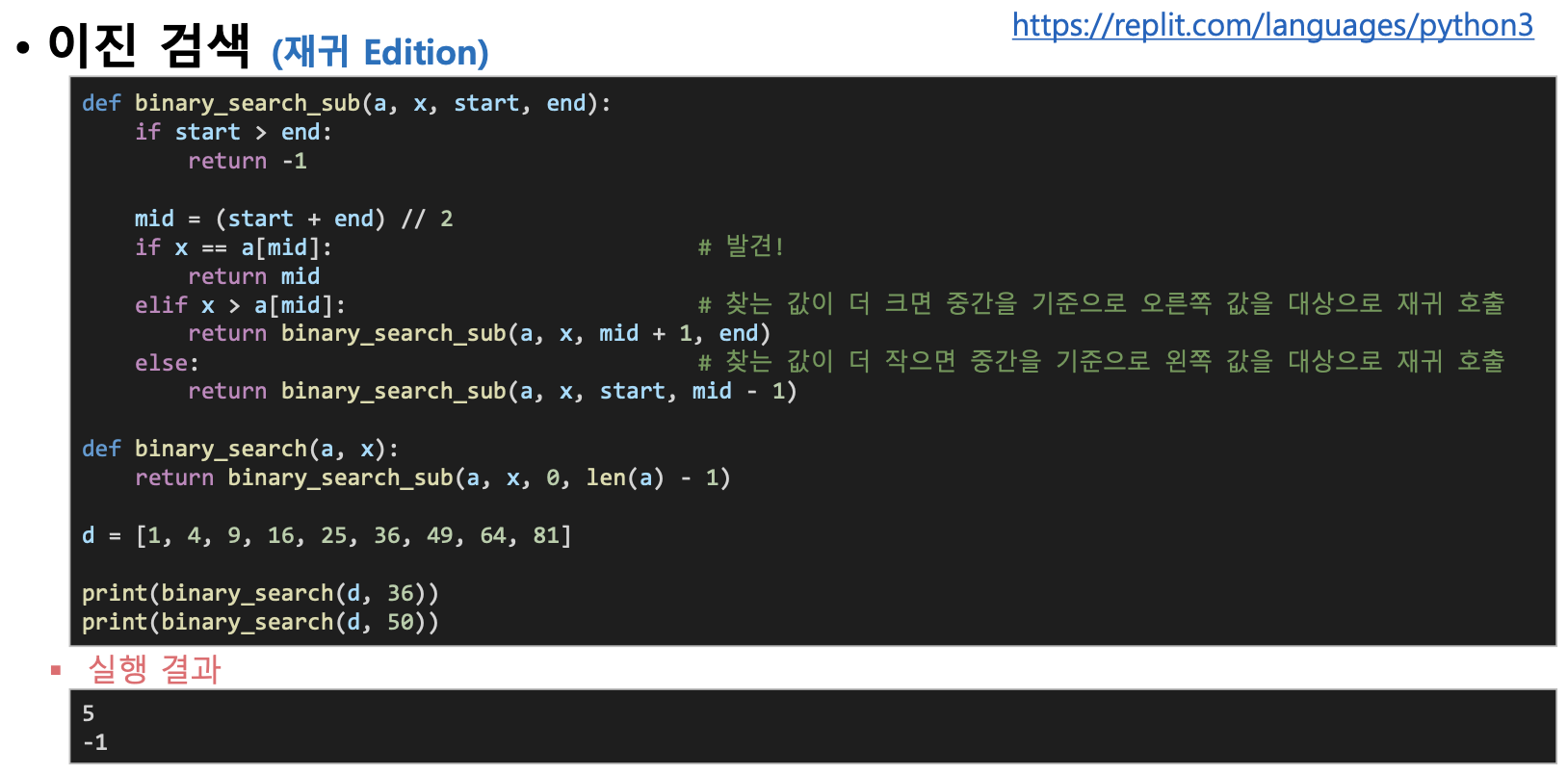
이진 검색을 재귀함수로
아래를 참고하여 재귀 호출을 사용한 이분 탐색 알고리즘을 생각해 보세요.
-
종료 조건: while문의 반복조건 반대로 생각하면 쉽다.
종료 조건이 호출되었을 때는? (반복에서 빠져나갔을 때) → 검색에 실패 (-1 반환) -
찾는 값과 주어진 탐색대상의 중간위치값을 비교
찾는 값과 중간 위치 값이 같다 → 검색에 성공 (위치 반환) -
찾는값이 중간위치값보다 크다 → 중간위치의 오른쪽을 대상으로 재귀호출 찾는 값이 중간 위치 값보다 작다 → 중간 위치의 왼쪽을 대상으로 재귀 호출
트리 검색
- 데이터 검색에는 상당히 효율적이지만 트리의 삽입, 삭제 등에는 부담
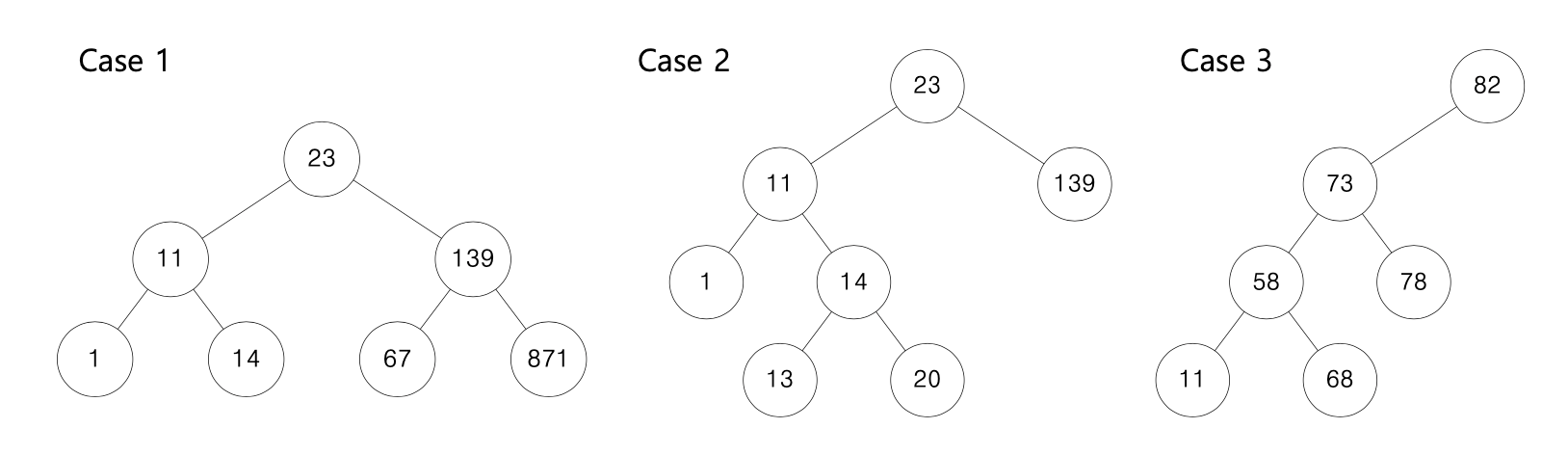
이진 검색 트리
• 이진 트리 중 활용도가 높은 트리로, 값 크기를 기준으로 일정 형태로 구성
각 노드가 다음 규칙을 따른다
• “왼쪽 자식 노드는 나보다 작고, 오른쪽 자식 노드는 나보다 크다.”
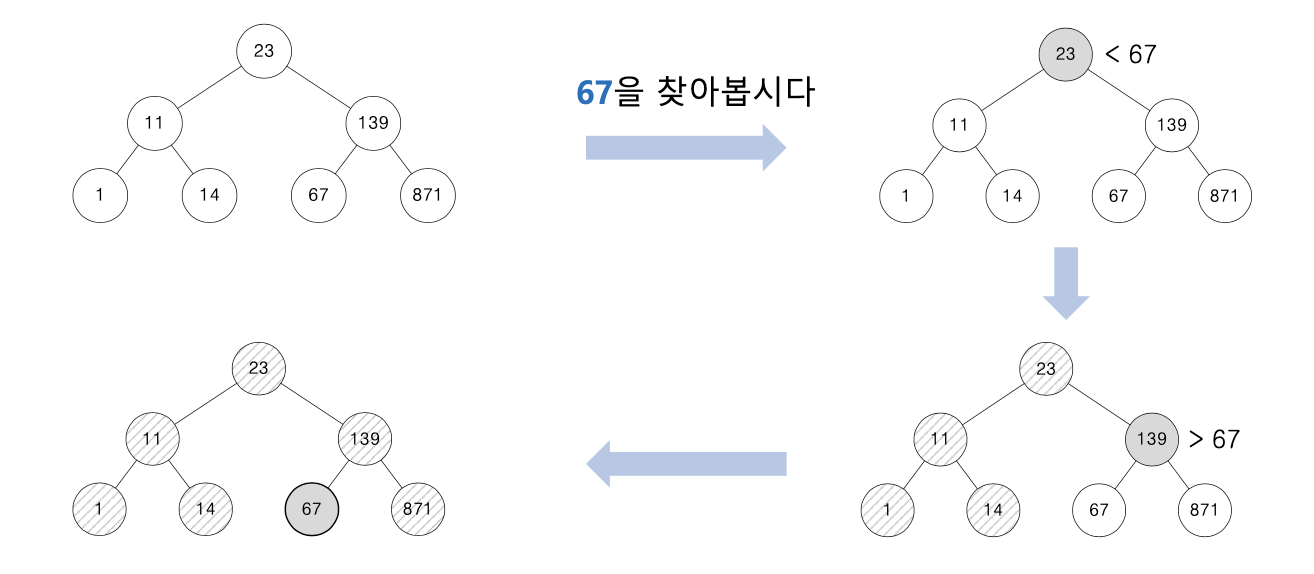
- 이진 검색 트리에서 값의 검색
• 매우 빠르게 (간단하게) 검색 가능
• 완전 이진 트리인 경우 → 𝐎(log2𝑛) =𝐎(log𝑛)
• 재귀의 방식 이용 가능
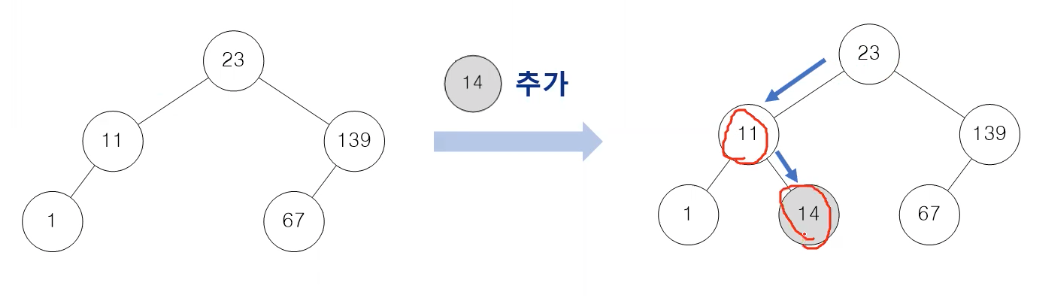
- 이진 검색 트리에서 값의 삽입
찾았을 때 True
None일 때 False
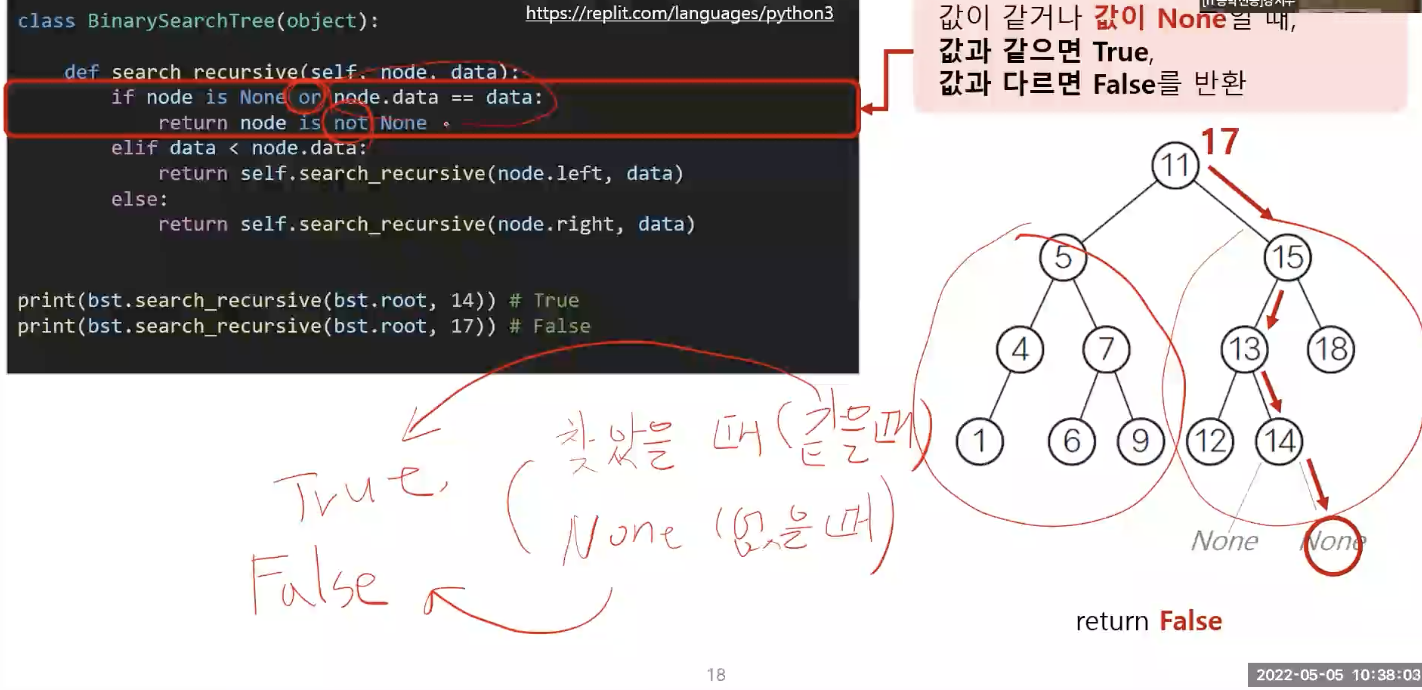
return node.data == data는 : True
중위 순회 검색 시 키값 오름차순
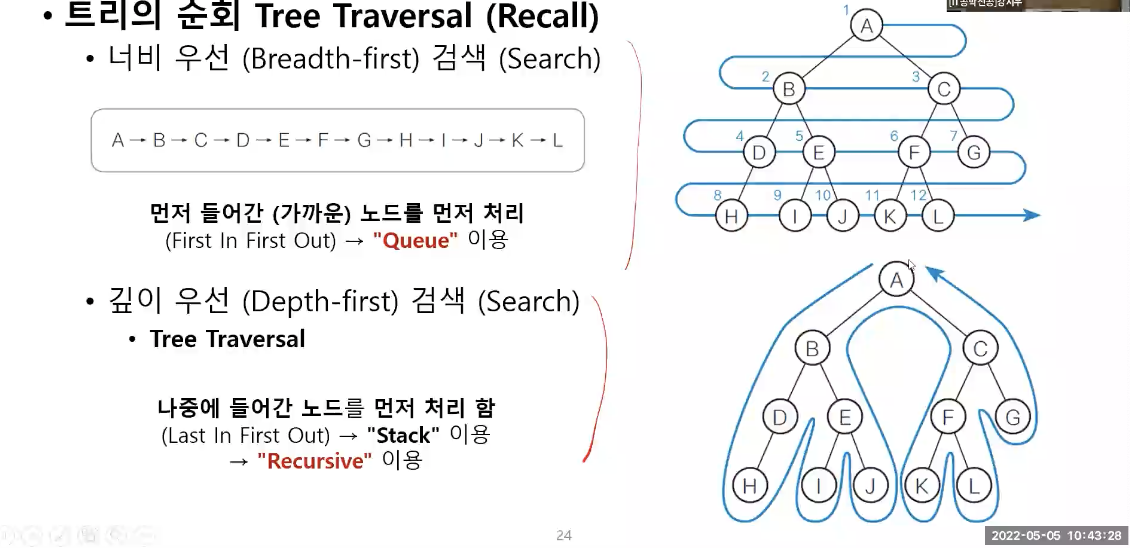
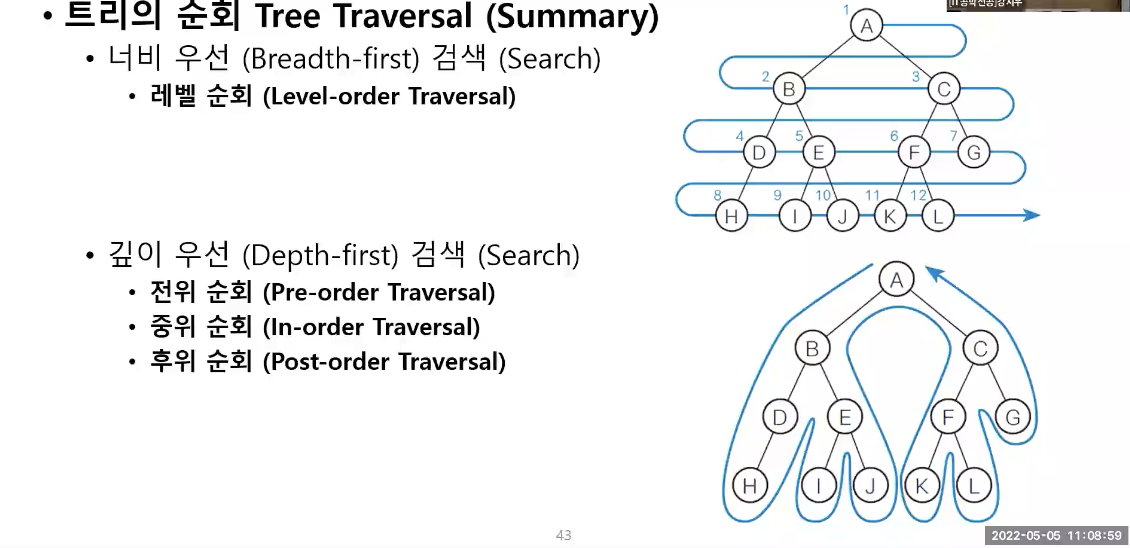
트리의 순회
Python List를 통한 Queue의 구현
가까운 애들부터 검색됨
bst.breadthfirst(bst.root) 너비 우선 검색
레벨 순서 순회임
그래프
그래프는 간선의 개수가 정해져 있지 않고, 일반적인 상하구조가 없음 / 값 가중치 부여 가능(유향 그래프) / 순서 상관 없음
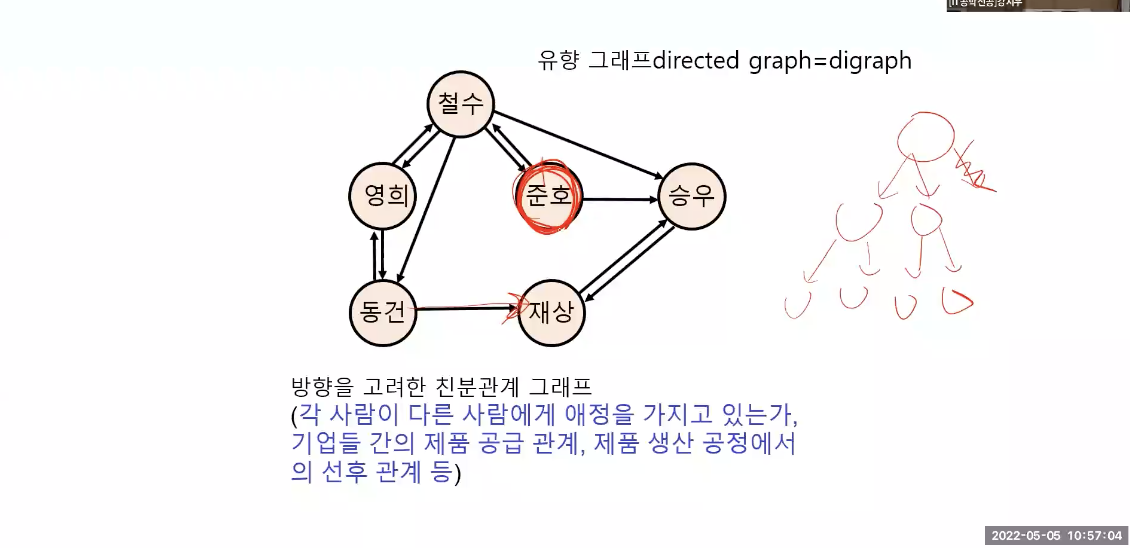
이진트리는 최대 두개이며 부모와 자식이라는 상하구조가 있음
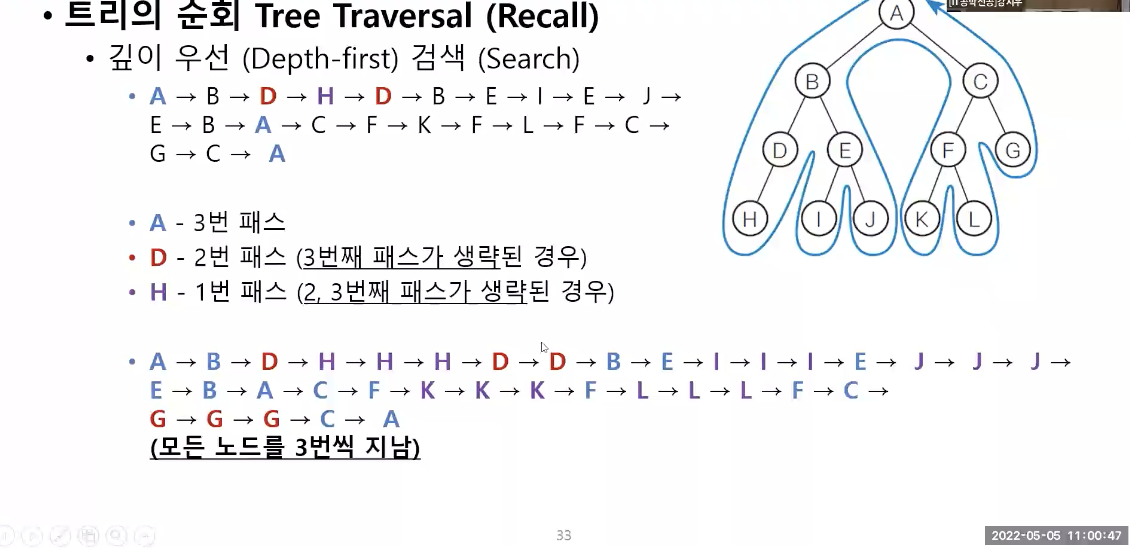
깊이 우선 검색(트리의 순회)
좌측-우측 자식 순으로 Node 재귀 순회
내 노드(꺼)가 처리되는 순서에 따라
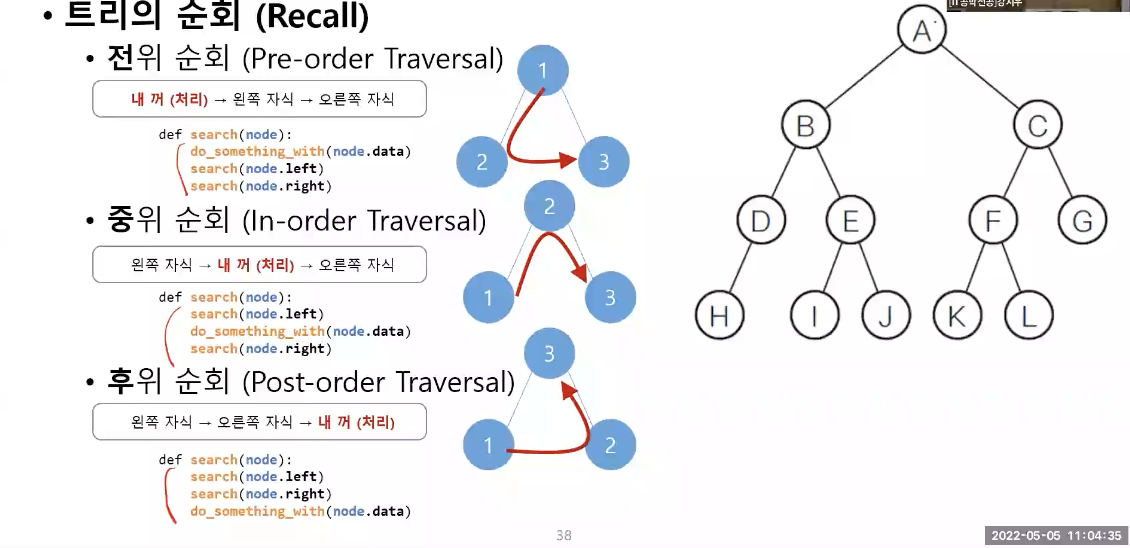
전위순회: bst.preorder
중위순회: bst.inorder
후위순회: bst.postorder
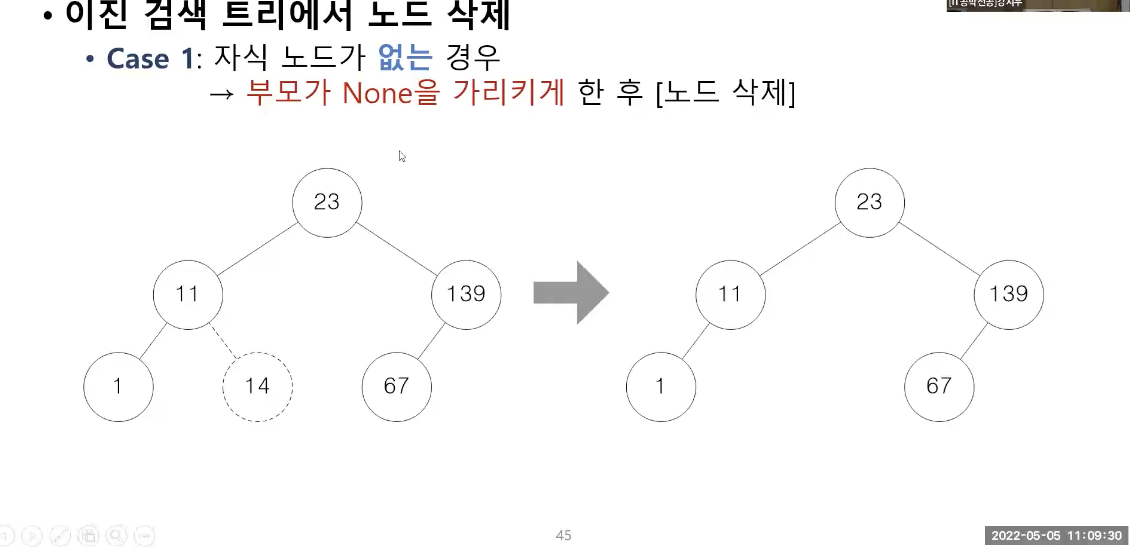
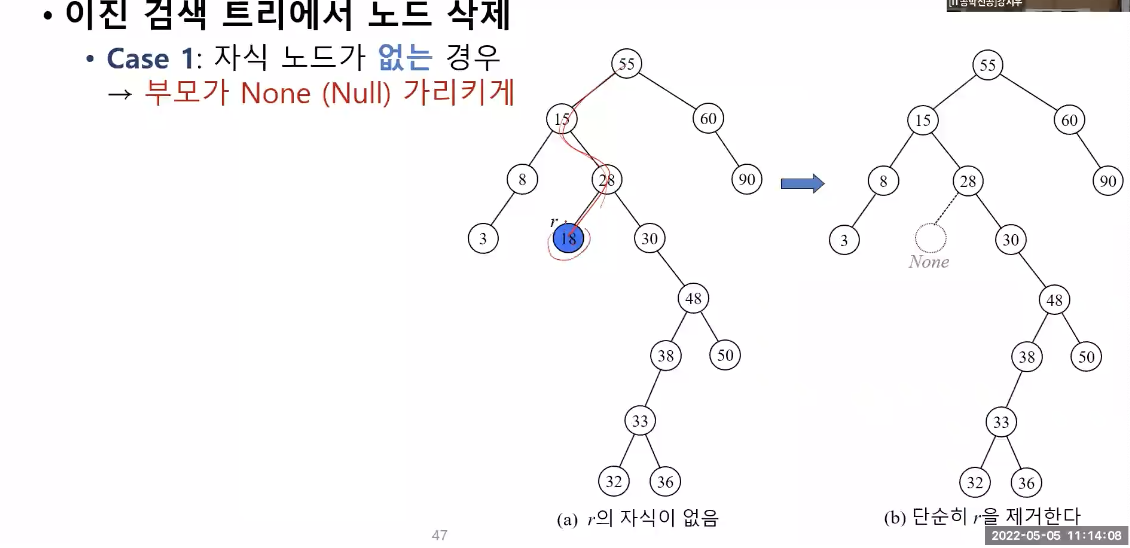
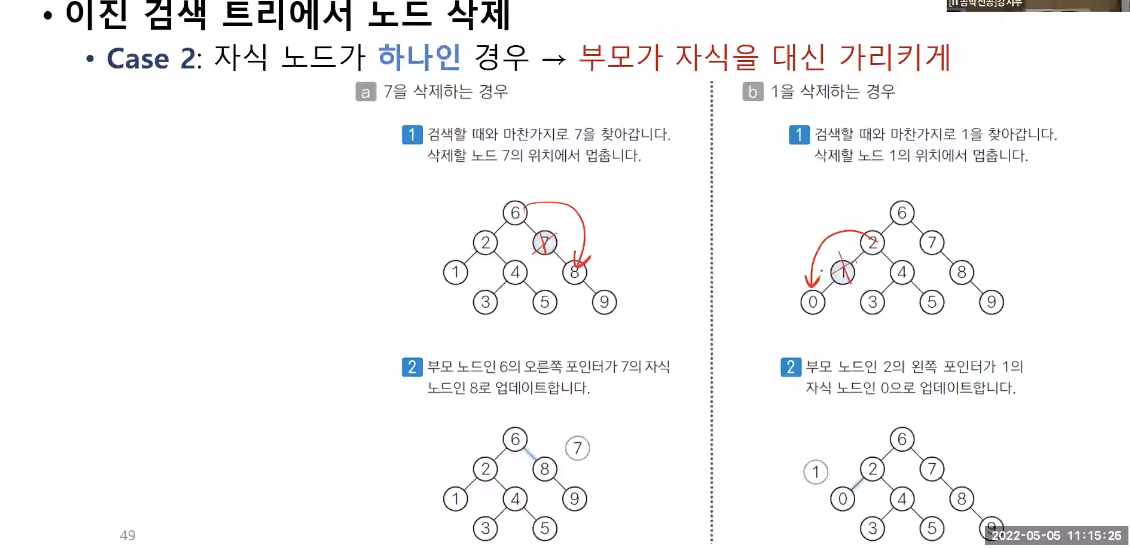
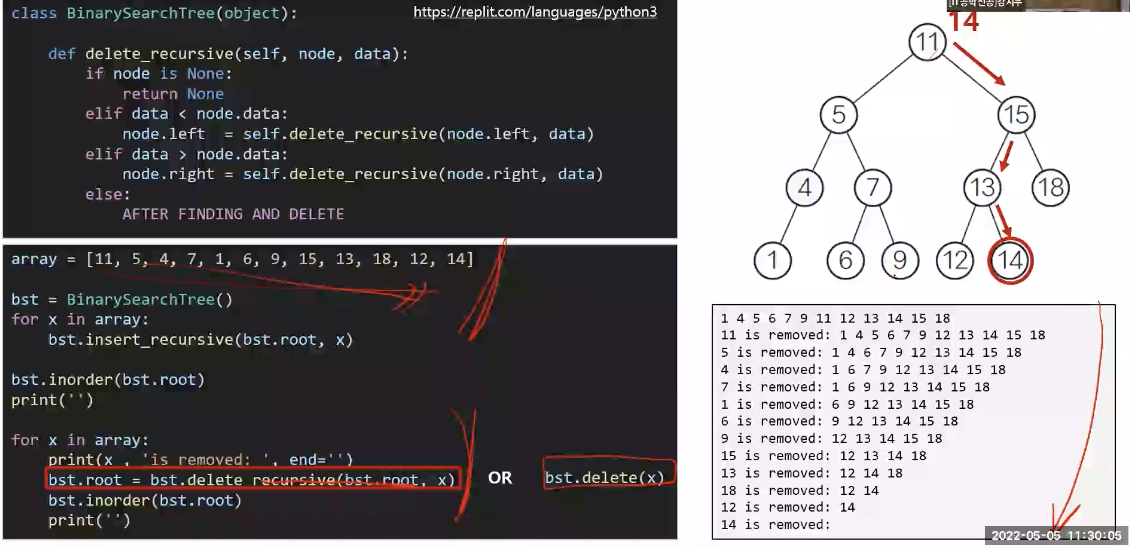
이진 검색 트리에서 노드 삭제

방법 1 : 자식 노드가 없는 경우
방법 2 : 자식 노드가 하나인 경우
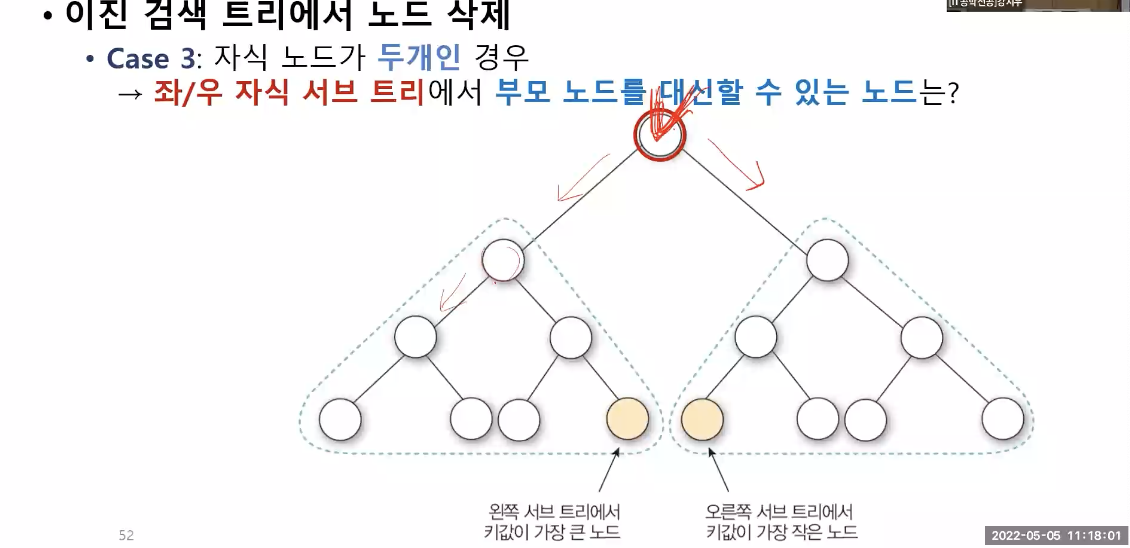
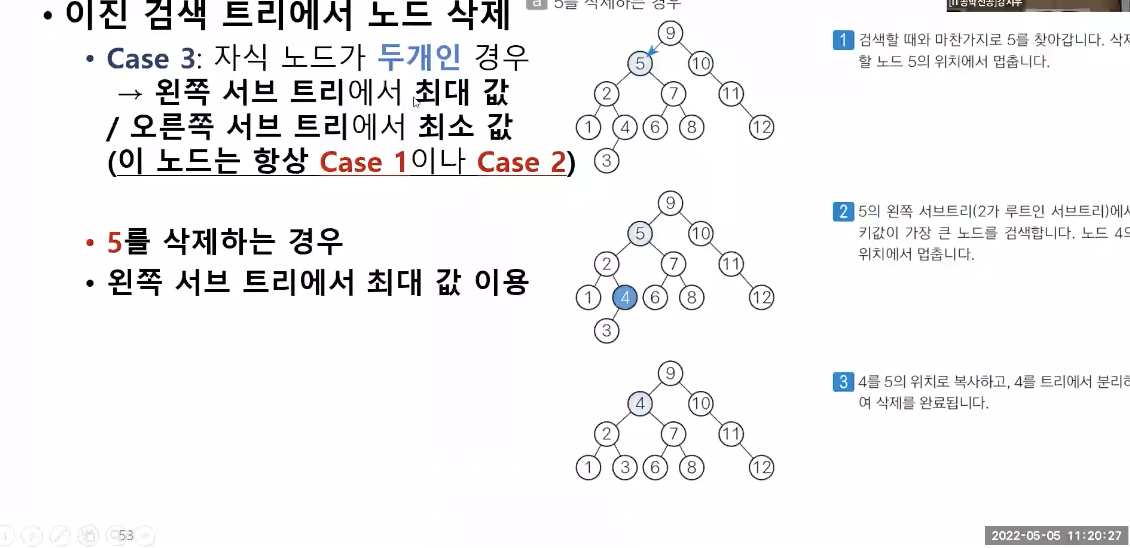
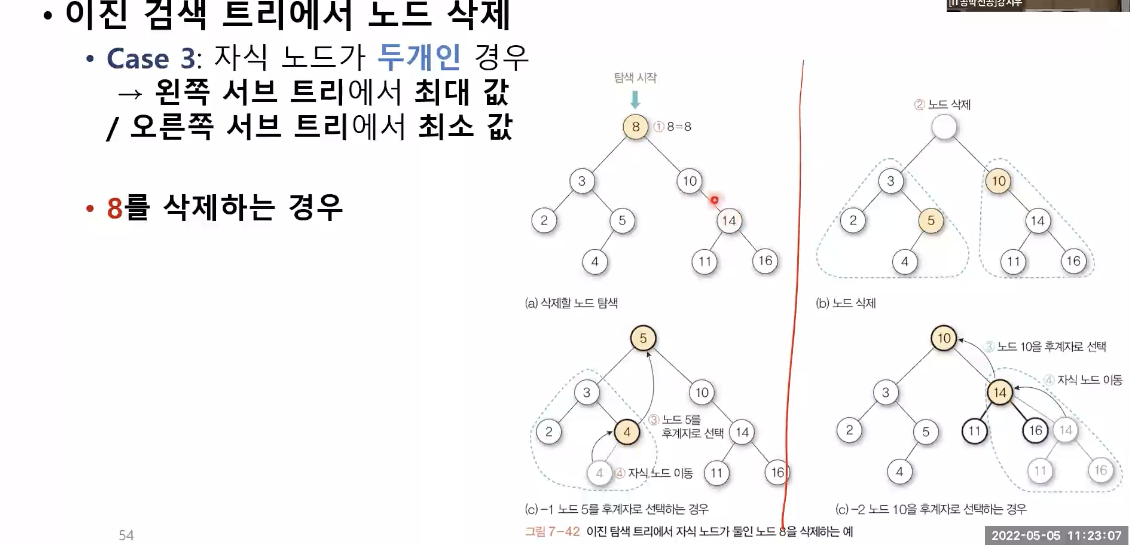
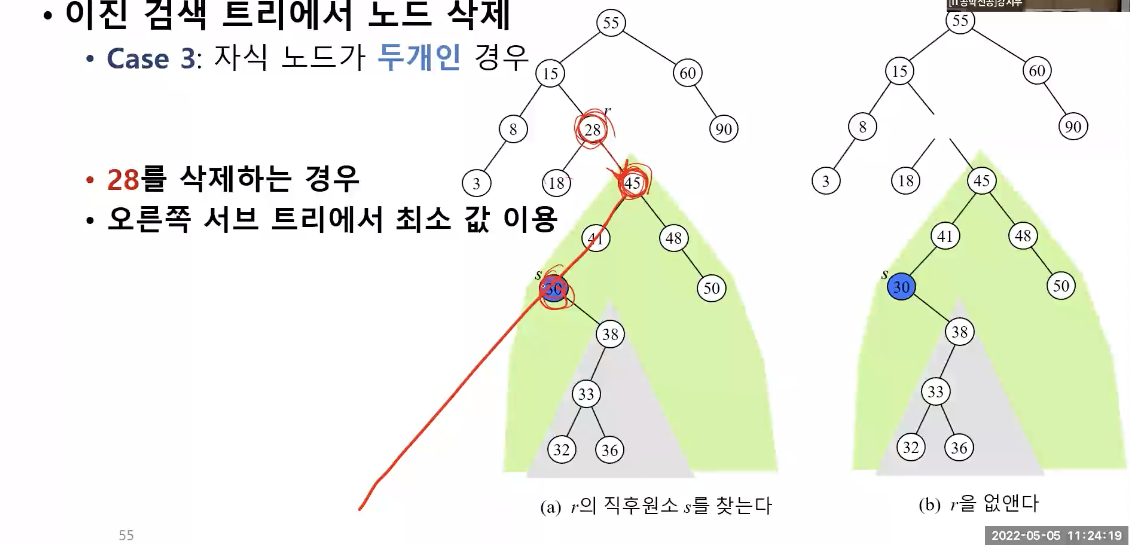
방법 3 : 자식 노드가 두 개인 경우
- 예제
+추가나 삭제는 포인터 값의 변경이 필요하므로 재귀함수를 짤 때 차이가 있다.
None or A : 이렇게 하면 안됨 (합리적인 제약이 아니다.)