1부터 n까지 연속한 숫자의 합을 구하는 문제를 풀기 위한 알고리즘
- 첫번째 방법 (숫자를 차례로 더하는 방법)
- 입력 값 n이 커질수록 덧셈을 훨씬 더 많이 반복해야 함
- n번의 복잡도 (계산량, 수행 시간)를 지닌다.
# 1부터 n까지 연속한 숫자의 합을 구하는 알고리즘 1
# 입력: n
# 출력: 1부터 n까지의 숫자를 더한 값
def sum_n(n):
s = 0 # 합을 계산할 변수
for i in range(1, n+1): # 1부터 n까지 반복(n + 1은 제외)
s = s + i
return s
print(sum_n(10)) # 실행결과: 50
print(sum_n(100) # 실행결과: 5050
- 두번째 방법
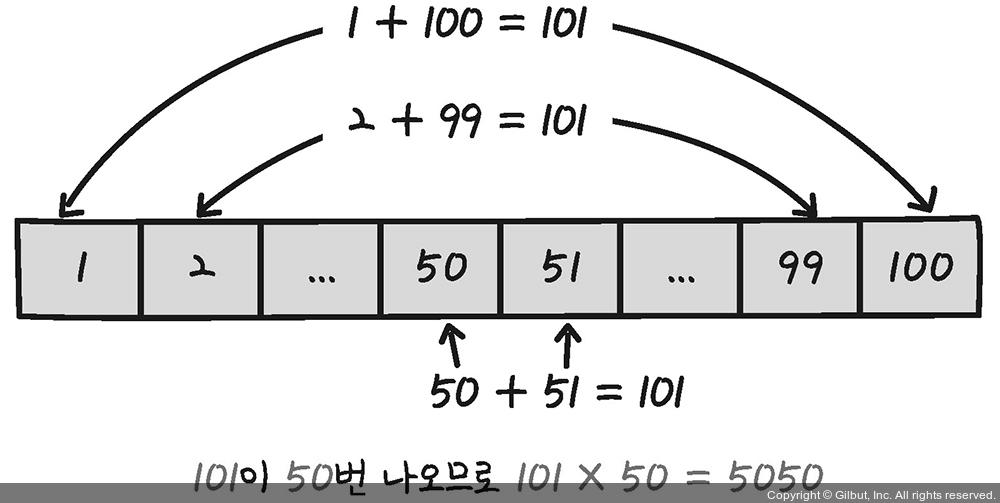
- n 값의 크기와 관계없이 덧셈, 곱셈, 나눗셈을 각각 한 번씩만 하면 답을 얻을 수 있음
- 3번의 복잡도를 지닌다.
# 1부터 n까지 연속한 숫자의 합을 구하는 알고리즘 2
# 입력: n
# 출력: 1부터 n까지의 숫자를 더한 값
def sum_n(n):
return (n * (n + 1)) // 2 #슬래시 두 개(//)는 정수 나눗셈
print(sum_n(10)) # 실행결과: 50
print(sum_n(100) # 실행결과: 5050
3. 1부터 n까지의 합 구하기를 재귀 알고리즘으로 구현
# 1부터 n까지 연속한 숫자의 합을 구하는 알고리즘
# 입력: n
# 출력: 1부터 n까지의 숫자를 더한 값
def sum_n(n):
if n < 2:
return 1
return n + sum_n(n-1)
print(sum_n(10)) # 실행결과: 55주어진 숫자 n개 중 가장 큰 숫자를 찾는 알고리즘
주어진 숫자 n개 중에서 가장 큰 숫자(최댓값)를 찾는 문제
- 17, 92, 18, 33, 58, 7, 33, 42와 같이 숫자가 여덟 개가 있을 때 최댓값 찾기
- 첫 번째 숫자 17을 최댓값으로 기억 (최댓값: 17)
- 두 번째 숫자 92를 현재 최댓값 17과 비교
92는 17보다 크므로 최댓값을 92로 바꿔 기억 (최댓값: 92)- 세 번째 숫자 18을 현재 최댓값 92와 비교
18은 92보다 작으므로 지나감 (최댓값: 92)
4~7. 네 번째 숫자부터 일곱 번째 숫자까지 같은 과정 반복- 마지막 숫자 42를 현재 최댓값 92와 비교
42는 92보다 작으므로 지나감 (최댓값: 92)- 마지막으로 기억된 92가 주어진 숫자 중 최댓값
# 최댓값 구하기
# 입력: 숫자가 n개 들어 있는 리스트
# 출력: 숫자 n개 중 최댓값
def find_max(a):
n = len(a) # 입력 크기 n
max_v = a[0] # 리스트의 첫 번째 값을 최댓값으로 기억
for i in range(1, n): # 1부터 n-1까지 반복
if a[i] > max_v: # 이번 값이 현재까지 기억된 최댓값보다 크면
max_v = a[i] # 최댓값을 변경
return max_v
v = [17, 92, 18, 33, 58, 7, 33, 42]
print(find_max(v)) # 실행결과: 922. 리스트에 있는 n개의 숫자 중에서 최댓값 찾기 알고리즘을 재귀 알고리즘으로 구현
# 최댓값 구하기
# 입력: 숫자가 n개 들어 있는 리스트
# 출력: 숫자 n개 중 최댓값
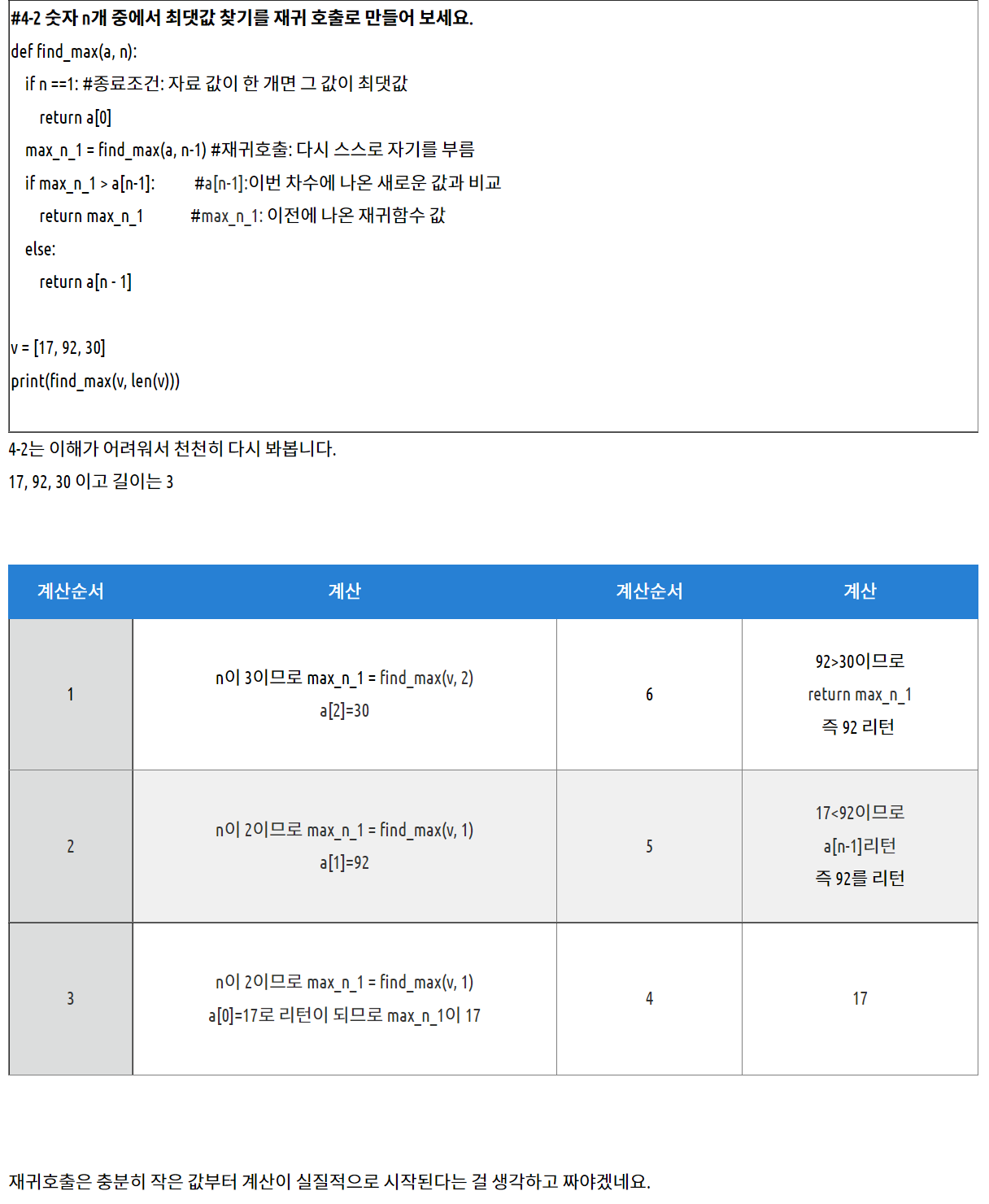
def find_max(v,n):
if n == 1:
return v[0]
max_v = find_max(v, n-1) # 재귀 호출
if (max_v > v[n-1]):
return max_v
else:
return v[n-1]
v = [17, 92, 18, 33, 58, 7, 33, 42]
print(find_max(v, len(v))) # 실행결과: 92
1부터 n까지 연속한 정수의 곱을 구하는 알고리즘
- 1부터 n까지의 곱, 즉 팩토리얼(Factorial) 문제
1! = 1
3! = 1 × 2 × 3 = 6
5! = 1 × 2 × 3 × 4 × 5 = 120
n! = 1 × 2 × 3 × … × (n -1) × n
단, 0!은 1이라고 약속합니다.
# 연속한 숫자의 곱을 구하는 알고리즘
# 입력: n
# 출력: 1부터 n까지 연속한 숫자를 곱한 값
def fact(n):
f = 1 # 곱을 계산할 변수, 초깃값은 1
for i in range(1, n + 1): # 1부터 n까지 반복(n + 1은 제외)
f = f * i # 곱셈 연산으로 수정
return f
print(fact(1)) # 1! = 1
print(fact(5)) # 5! = 120
print(fact(10)) # 10! = 3628800- 알고리즘 분석
for 반복문을 이용한 프로그램의 경우 n!을 구하려면 곱셈이 n번 필요
하노이의 탑 알고리즘
원반이 한 개일 때가 바로 ‘종료 조건’에 해당한다. 원반 n개 문제를 풀려면 n-1개 원반 문제를 풀어야 하는데, 이는 바로 ‘좀 더 작은 값으로 자기 자신을 호출’하는 과정이다. 따라서 이 문제는 전형적인 재귀 호출 알고리즘에 해당한다.
# 하노이의 탑
# 입력: 옮기려는 원반의 개수 n
# 옮길 원반이 현재 있는 출발점 기둥 from_pos
# 원반을 옮길 도착점 기둥 to_pos
# 옮기는 과정에서 사용할 보조 기둥 aux_pos
# 출력: 원반을 옮기는 순서
def hanoi(n, from_pos, to_pos, aux_pos):
if n == 1: # 원반 한 개를 옮기는 문제면 그냥 옮기면 됨
print(from_pos, ”->“, to_pos)
return
# 원반 n -1개를 aux_pos로 이동(to_pos를 보조 기둥으로)
hanoi(n -1, from_pos, aux_pos, to_pos)
# 가장 큰 원반을 목적지로 이동
print(from_pos, ”->“, to_pos)
# aux_pos에 있는 원반 n -1개를 목적지로 이동(from_pos를 보조 기둥으로)
hanoi(n - 1, aux_pos, to_pos, from_pos)
print(“n = 1”)
hanoi(1, 1, 3, 2) # 원반 한 개를 1번 기둥에서 3번 기둥으로 이동(2번을 보조 기둥으로)
print(“n = 2”)
hanoi(2, 1, 3, 2) # 원반 두 개를 1번 기둥에서 3번 기둥으로 이동(2번을 보조 기둥으로)
print(“n = 3”)
hanoi(3, 1, 3, 2) # 원반 세 개를 1번 기둥에서 3번 기둥으로 이동(2번을 보조 기둥으로)- 실행 결과
n = 1 # hanoi(1, 1, 3, 2)
1 -> 3 # print(1,”->“,3)
n = 2 # hanoi(2, 1, 3, 2)
1 -> 2 # hanoi(1, 1, 2, 3)
1 -> 3 # print(1,”->“,3)
2 -> 3 # hanoi(1, 2, 3, 1)
n = 3
1 -> 3
1 -> 2
3 -> 2
1 -> 3
2 -> 1
2 -> 3
1 -> 3선택 정렬
‘키 순서로 줄 세우기’는 대표적인 정렬 문제의 예이다.
왜냐하면, 이 문제는 ‘학생의 키라는 자료 값을 작은 것부터 큰 순서로 나열하라’는 문제와 같은 말이기 때문이다.
1 . 학생 열 명이 모여 있는 운동장에 선생님이 등장합니다.
2 . 선생님은 학생들을 둘러보며 키가 가장 작은 사람을 찾습니다. 키가 가장 작은 학생으로 ‘선택’된 민준이가 불려 나와 맨 앞에 섭니다. 민준이가 나갔으므로 이제 학생은 아홉 명 남았습니다.
3 . 이번에는 선생님이 학생 아홉 명 중 키가 가장 작은 성진이를 선택합니다. 선택된 성진이가 불려 나와 민준이 뒤로 줄을 섭니다.
4 . 이처럼 남아 있는 학생 중에서 키가 가장 작은 학생을 한 명씩 뽑아 줄에 세우는 과정을 반복하면 모든 학생이 키 순서에 맞춰 줄을 서게 됩니다.
쉽게 설명한 선택 정렬 알고리즘
# 쉽게 설명한 선택 정렬
# 입력: 리스트 a
# 출력: 정렬된 새 리스트
# 주어진 리스트에서 최솟값의 위치를 돌려주는 함수
def find_min_idx(a):
n = len(a)
min_idx = 0
for i in range(1, n):
if a[i] < a[min_idx]:
min_idx = i
return min_idx
def sel_sort(a):
result = [] # 새 리스트를 만들어 정렬된 값을 저장
while a: # 주어진 리스트에 값이 남아 있는 동안 계속
min_idx = find_min_idx(a) # 리스트에 남아 있는 값 중 최솟값의 위치
value = a.pop(min_idx) # 찾은 최솟값을 빼내어 value에 저장
result.append(value) # value를 결과 리스트 끝에 추가
return result
d = [2, 4, 5, 1, 3]
print(sel_sort(d)) # 실행결과: [1, 2, 3, 4, 5]일반적인 선택 정렬 알고리즘
‘일반적인 선택 정렬 알고리즘’은 입력으로 주어진 리스트 a 안에서 직접 자료의 위치를 바꾸면서 정렬시키는 프로그램이다.
# 선택 정렬
# 입력: 리스트 a
# 출력: 없음(입력으로 주어진 a가 정렬됨)
def sel_sort(a):
n = len(a)
for i in range(0, n - 1): # 0부터 n -2까지 반복
# i번 위치부터 끝까지 자료 값 중 최솟값의 위치를 찾음
min_idx = i
for j in range(i + 1, n):
if a[j] < a[min_idx]:
min_idx = j
# 찾은 최솟값을 i번 위치로
a[i], a[min_idx] = a[min_idx], a[i]
d = [2, 4, 5, 1, 3]
sel_sort(d)
print(d) # 실행결과: [1, 2, 3, 4, 5]내림차순 정렬
오름차순 선택 정렬에서 최솟값 대신 최댓값을 선택하면 내림차순 정렬(큰 수에서 작은 수로 나열)이 된다.
다음과 같이 비교 부등호 방향을 작다(< )에서 크다( >)로 바꾸기만 해도 내림차순 정렬 프로그램이 된다. 여기서는 변수 이름의 의미를 맞추려고 변수 min_idx를 max_idx로 바꾸었다.
# 내림차순 선택 정렬
# 입력: 리스트 a
# 출력: 없음(입력으로 주어진 a가 정렬됨)
def sel_sort(a):
n = len(a)
for i in range(0, n - 1):
max_idx = i # 최솟값(min) 대신 최댓값(max)을 찾아야 함
for j in range(i + 1, n):
if a[j] > a[max_idx]: # 부등호 방향 뒤집기
max_idx = j
a[i], a[max_idx] = a[max_idx], a[i]
d = [2, 4, 5, 1, 3]
sel_sort(d)
print(d)List [2, 5, 6, 3, 1]을 선택 정렬하는 과정을 적어보세요.
def sel_sort(a):
n = len(a)
for i in range(0, n - 1):
min_idx = i
for j in range(i + 1, n):
if a[j] < a[min_idx]:
min_idx = j
a[i], a[min_idx] = a[min_idx], a[i]
print(a) # 정렬 과정 출력하기
d = [2, 5, 6, 3, 1]
sel_sort(d)
print(d)실행결과

거품 정렬
- 서로 인접한 두 원소를 검사하여 정렬하는 알고리즘
- 인접한 2개의 레코드를 비교하여 크기가 순서대로 되어 있지 않으면 서로 교환한다.
- 선택 정렬과 기본 개념이 유사하다.
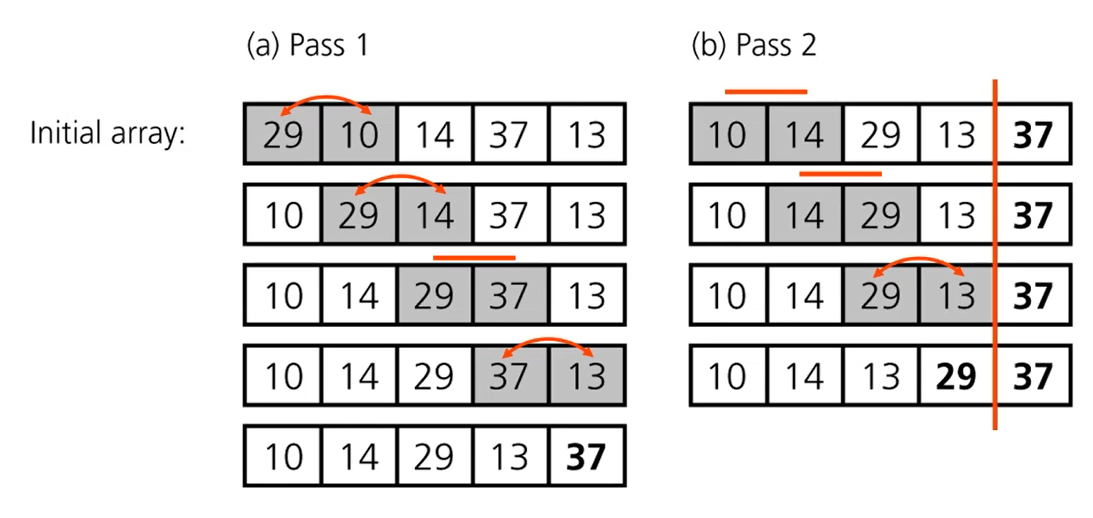
-
버블 정렬은 첫 번째 자료와 두 번째 자료를, 두 번째 자료와 세 번째 자료를, 세 번째와 네 번째를, … 이런 식으로 (마지막-1)번째 자료와 마지막 자료를 비교하여 교환하면서 자료를 정렬한다.
-
1회전을 수행하고 나면 가장 큰 자료가 맨 뒤로 이동하므로 2회전에서는 맨 끝에 있는 자료는 정렬에서 제외되고, 2회전을 수행하고 나면 끝에서 두 번째 자료까지는 정렬에서 제외된다. 이렇게 정렬을 1회전 수행할 때마다 정렬에서 제외되는 데이터가 하나씩 늘어난다.
거품 정렬 알고리즘(오름차순)
# 거품 정렬
# 입력: 리스트 a
# 출력: 없음(입력으로 주어진 a가 정렬됨)
def bubble_sort(a):
n = len(a)
for i in range(n):
for j in range(0, n - i - 1):
if a[j] > a[j + 1]: # 앞이 뒤보다 크면
print(a) # 정렬 과정 출력(참고용)
a[j], a[j + 1] = a[j + 1], a[j] # 두 자료의 위치를 맞바꿈
d = [2, 4, 5, 1, 3]
bubble_sort(d)
print(d) # 실행결과: [1, 2, 3, 4, 5]- 실행결과
[2, 4, 5, 1, 3]
[2, 4, 1, 5, 3]
[2, 4, 1, 3, 5]
[2, 1, 4, 3, 5]
[2, 1, 3, 4, 5]
[1, 2, 3, 4, 5]내림차순 정렬
# 거품 정렬
# 입력: 리스트 a
# 출력: 없음(입력으로 주어진 a가 정렬됨)
def bubble_sort(a):
n = len(a)
for i in range(n):
for j in range(0, n - i - 1):
if a[j] < a[j + 1]: # 뒤가 앞보다 크면
print(a) # 정렬 과정 출력(참고용)
a[j], a[j + 1] = a[j + 1], a[j] # 두 자료의 위치를 맞바꿈
d = [2, 4, 5, 1, 3]
bubble_sort(d)
print(d) # 실행결과: [5, 4, 3, 2, 1]List[2,5,6,3,1]을 거품정렬하는 과정
[2, 5, 6, 3, 1]
[5, 2, 6, 3, 1]
[5, 6, 2, 3, 1]
[5, 6, 3, 2, 1]
[6, 5, 3, 2, 1]삽입정렬
1 | 학생이 열 명 모인 운동장에 선생님이 등장합니다.
2 | 선생님은 열 명 중 제일 앞에 있던 승규에게 나와서 줄을 서라고 합니다. 승규가 나갔으니 이제 학생이 아홉 명 남았습니다.
3 | 이번에는 선생님이 준호에게 키를 맞춰 줄을 서라고 합니다. 준호는 이미 줄을 선 승규보다 자신이 키가 작은 것을 확인하고 승규 앞에 섭니다.
4 | 남은 여덟 명 중 이번에는 민성이가 뽑혀 줄을 섭니다. 민성이는 준호보다 크고 승규보다는 작습니다. 그래서 준호와 승규 사이에 공간을 만들어 줄을 섭니다(삽입).
5 | 마찬가지로 남은 학생을 한 명씩 뽑아 이미 줄을 선 학생 사이사이에 키를 맞춰 끼워 넣는 일을 반복합니다. 마지막 남은 학생까지 뽑아서 줄을 세우면 모든 학생이 제자리에 줄을 서게 됩니다.

쉽게 설명한 삽입 정렬 알고리즘
# 쉽게 설명한 삽입 정렬
# 입력: 리스트 a
# 출력: 정렬된 새 리스트
# 리스트 r에서 v가 들어가야 할 위치를 돌려주는 함수
def find_ins_idx(r, v):
# 이미 정렬된 리스트 r의 자료를 앞에서부터 차례로 확인하여
for i in range(0, len(r)):
# v 값보다 i번 위치에 있는 자료 값이 크면
# v가 그 값 바로 앞에 놓여야 정렬 순서가 유지됨
if v < r[i]:
return i
# 적절한 위치를 못 찾았을 때는
# v가 r의 모든 자료보다 크다는 뜻이므로 맨 뒤에 삽입
return len(r)
def ins_sort(a):
result = [] # 새 리스트를 만들어 정렬된 값을 저장
while a: # 기존 리스트에 값이 남아 있는 동안 반복
value = a.pop(0) # 기존 리스트에서 한 개를 꺼냄
ins_idx = find_ins_idx(result, value) # 꺼낸 값이 들어갈 적당한 위치 찾기
result.insert(ins_idx, value) # 찾은 위치에 값 삽입(이후 값은 한 칸씩 밀려남)
return result
d = [2, 4, 5, 1, 3]
print(ins_sort(d)) # 실행결과: [1, 2, 3, 4, 5]일반적인 삽입 정렬 알고리즘
# 삽입 정렬
# 입력: 리스트 a
# 출력: 없음(입력으로 주어진 a가 정렬됨)
def ins_sort(a):
n = len(a)
for i in range(1, n): # 1부터 n -1까지
key = a[i] # i번 위치에 있는 값을 key에 저장
# j를 i 바로 왼쪽 위치로 저장
j = i - 1
# 리스트의 j번 위치에 있는 값과 key를 비교해 key가 삽입될 적절한 위치를 찾음
while j >= 0 and a[j] > key:
a[j + 1] = a[j] # 삽입할 공간이 생기도록 값을 오른쪽으로 한 칸 이동
j -= 1
a[j + 1] = key # 찾은 삽입 위치에 key를 저장
d = [2, 4, 5, 1, 3]
ins_sort(d)
print(d) # 실행결과: [1, 2, 3, 4, 5]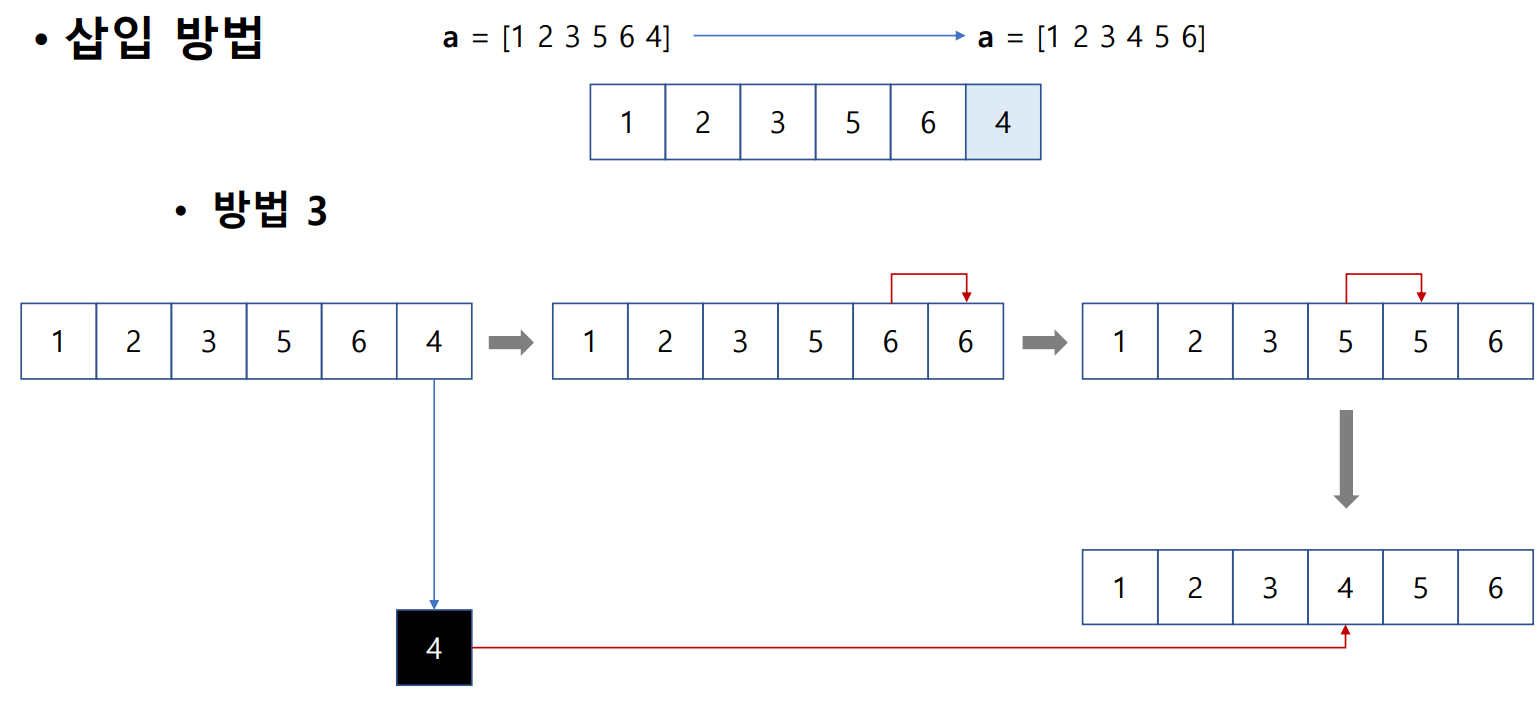
내림차순 정렬
# 삽입 정렬
# 입력: 리스트 a
# 출력: 없음(입력으로 주어진 a가 정렬됨)
def ins_sort(a):
n = len(a)
for i in range(1, n): # 1부터 n -1까지
key = a[i] # i번 위치에 있는 값을 key에 저장
# j를 i 바로 왼쪽 위치로 저장
j = i - 1
# 리스트의 j번 위치에 있는 값과 key를 비교해 key가 삽입될 적절한 위치를 찾음
while j >= 0 and a[j] < key:
a[j + 1] = a[j] # 삽입할 공간이 생기도록 값을 오른쪽으로 한 칸 이동
j -= 1
a[j + 1] = key # 찾은 삽입 위치에 key를 저장
d = [2, 4, 5, 1, 3]
ins_sort(d)
print(d) # 실행결과: [5, 4, 3, 2, 1]List [2, 5, 6, 3, 1]을 삽입 정렬하는 과정을 적어보세요.
i=0, j=0
[5,2,6,3,1]
i=0, j=1
[5,6,2,3,1]
i=0, j=2
[5,6,3,2,1]
i=0, j=3
[5,6,3,2,1]
i=1, j=0
[6,5,3,2,1]병합 정렬
1 | 학생들에게 일일이 지시하는 것이 귀찮아진 선생님은 학생들이 알아서 줄을 설 수 있는 방법이 없을지 고민입니다. 열 명이나 되는 학생들에게 동시에 알아서 줄을 서라고 하면 너무 소란스러울 것 같아서, 다섯 명씩 두 조로 나누어 그 안에서 키 순서로 줄을 서라고 시켰습니다.
2 | 이제 선생님 앞에는 키 순서대로 정렬된 두 줄(중간 결과 줄)이 있습니다.
3 | 선생님은 각 줄의 맨 앞에 있는 두 학생 중에 키가 더 작은 민수를 뽑아 최종 결과 줄에 세웁니다. 그리고 다시 각 중간 결과 줄의 맨 앞에 있는 두 학생을 비교해 더 작은 학생을 최종 결과 줄의 민수 뒤에 세웁니다.
4| 이 과정을 반복하다가 중간 결과 줄 하나가 사라지면 나머지 중간 결과 줄에 있는 사람을 전부 최종 결과 줄에 세웁니다.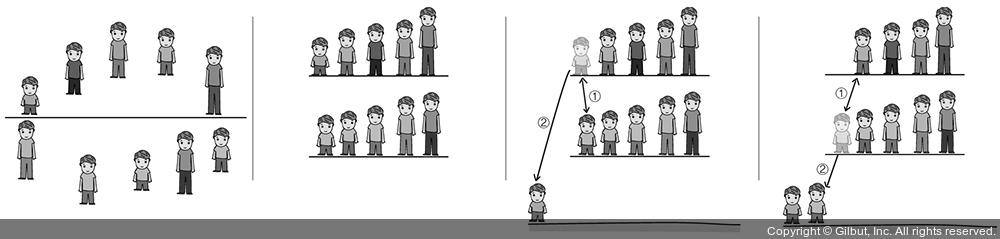
쉽게 설명한 병합 정렬 알고리즘
# 쉽게 설명한 병합 정렬
# 입력: 리스트 a
# 출력: 정렬된 새 리스트
def merge_sort(a):
n = len(a)
# 종료 조건: 정렬할 리스트의 자료 개수가 한 개 이하이면 정렬할 필요 없음
if n <= 1:
return a
# 그룹을 나누어 각각 병합 정렬을 호출하는 과정
mid = n // 2 # 중간을 기준으로 두 그룹으로 나눔
g1 = merge_sort(a[:mid]) # 재귀 호출로 첫 번째 그룹을 정렬
g2 = merge_sort(a[mid:]) # 재귀 호출로 두 번째 그룹을 정렬
# 두 그룹을 하나로 병합
result = [] # 두 그룹을 합쳐 만들 최종 결과
while g1 and g2: # 두 그룹에 모두 자료가 남아 있는 동안 반복
if g1[0] < g2[0]: # 두 그룹의 맨 앞 자료 값을 비교
# g1 값이 더 작으면 그 값을 빼내어 결과로 추가
result.append(g1.pop(0))
else:
# g2 값이 더 작으면 그 값을 빼내어 결과로 추가
result.append(g2.pop(0))
# 아직 남아 있는 자료들을 결과에 추가
# g1과 g2 중 이미 빈 것은 while을 바로 지나감
while g1:
result.append(g1.pop(0))
while g2:
result.append(g2.pop(0))
return result
d = [6, 8, 3, 9, 10, 1, 2, 4, 7, 5]
print(merge_sort(d))- 실행결과
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]일반적인 병합 정렬 알고리즘
정렬 원리는 같지만, return 값이 없고 입력 리스트 안의 자료 순서를 직접 바꾼다는 차이가 있다.
# 병합 정렬
# 입력: 리스트 a
# 출력: 없음(입력으로 주어진 a가 정렬됨)
def merge_sort(a):
n = len(a)
# 종료 조건: 정렬할 리스트의 자료 개수가 한 개 이하이면 정렬할 필요가 없음
if n <= 1:
return
# 그룹을 나누어 각각 병합 정렬을 호출하는 과정
mid = n // 2 # 중간을 기준으로 두 그룹으로 나눔
g1 = a[:mid]
g2 = a[mid:]
merge_sort(g1) # 재귀 호출로 첫 번째 그룹을 정렬
merge_sort(g2) # 재귀 호출로 두 번째 그룹을 정렬
# 두 그룹을 하나로 병합
i1 = 0
i2 = 0
ia = 0
while i1 < len(g1) and i2 < len(g2):
if g1[i1] < g2[i2]:
a[ia] = g1[i1]
i1 += 1
ia += 1
else:
a[ia] = g2[i2]
i2 += 1
ia += 1
# 아직 남아 있는 자료들을 결과에 추가
while i1 < len(g1):
a[ia] = g1[i1]
i1+= 1
ia += 1
while i2 < len(g2):
a[ia] = g2[i2]
i2 += 1
ia += 1
d = [6, 8, 3, 9, 10, 1, 2, 4, 7, 5]
merge_sort(d)
print(d)- 실행결과
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]- 예시
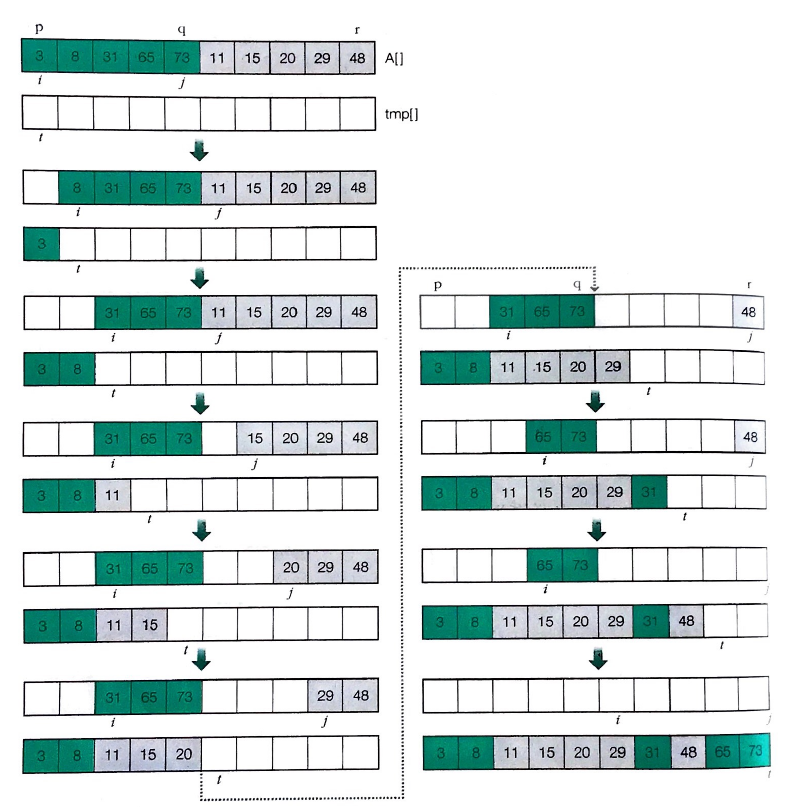
내림차순 정렬
오름차순 정렬에서 값을 비교하는 부분(g1[i1] < g2[i2])의 부등호 방향을 반대로 하면 내림차순 정렬 프로그램이 된다.
# 내림차순 병합 정렬
# 입력: 리스트 a
# 출력: 없음(입력으로 주어진 a가 정렬됨)
def merge_sort(a):
n = len(a)
# 종료 조건: 정렬할 리스트의 자료 개수가 한 개 이하이면 정렬할 필요가 없음
if n <= 1:
return
# 그룹을 나누어 각각 병합 정렬을 호출하는 과정
mid = n // 2
g1 = a[:mid]
g2 = a[mid:]
merge_sort(g1)
merge_sort(g2)
# 두 그룹을 합치는 과정(병합)
i1 = 0
i2 = 0
ia = 0
while i1 < len(g1) and i2 < len(g2):
if g1[i1] > g2[i2]: # 부등호 방향 뒤집기
a[ia] = g1[i1]
i1 += 1
ia += 1
else:
a[ia] = g2[i2]
i2 += 1
ia += 1
while i1 < len(g1):
a[ia] = g1[i1]
i1 += 1
ia += 1
while i2 < len(g2):
a[ia] = g2[i2]
i2 += 1
ia += 1
d = [6, 8, 3, 9, 10, 1, 2, 4, 7, 5]
merge_sort(d)
print(d)List [2, 5, 6, 3, 1]을 병합 정렬하는 과정을 적어보세요.
1. 배열을 반반으로 나눈다.
l1 = [2,5]
l2 = [6,3,1]
2. 각각 독립적으로 정렬한다(오름차순).
l1 = [2,5]
l2 = [1,3,6]
3. 두 집단 중 맨 앞 값을 비교해서, 더 작은 값을 뽑아 새로운 배열에 추가
result =[1]
result = [1,2]
result = [1,2,3]
result = [1,2,3,5]
4. 한 집단의 값이 모두 뽑히면, 다른 값이 남은 집단의 값을 모두 새로운 배열에 이어 붙임
result = [1,2,3,5,6]퀵 정렬
1 | 학생들에게 일일이 지시하는 것이 귀찮아진 선생님은 학생들이 알아서 줄을 서는 방법이 없을지 고민입니다. 그렇다고 열 명이나 되는 학생들에게 한 번에 알아서 줄을 서라고 하면 소란스러울 것 같아 조를 나누려고 합니다.
2 | 열 명 중에 기준이 될 사람을 한 명 뽑습니다. 기준으로 뽑은 태호를 줄 가운데 세운 다음 태호보다 키가 작은 학생은 태호 앞에, 태호보다 큰 학생은 태호 뒤에 서게 합니다(학생들은 태호하고만 키를 비교하면 됩니다).
3 | 기준인 태호는 가만히 있고, 태호보다 키가 작은 학생은 작은 학생들끼리, 큰 학생은 큰 학생들끼리 다시 키 순서대로 줄을 서면 줄 서기가 끝납니다.

쉽게 설명한 퀵 정렬 알고리즘

Pivot을 기준으로 좌우로 나누는 것을 Partitioning
# 쉽게 설명한 퀵 정렬
# 입력: 리스트 a
# 출력: 정렬된 새 리스트
def quick_sort(a):
n = len(a)
# 종료 조건: 정렬할 리스트의 자료 개수가 한 개 이하이면 정렬할 필요가 없음
if n <= 1:
return a
# 기준 값을 정하고 기준에 맞춰 그룹을 나누는 과정
pivot = a[-1] # 편의상 리스트의 마지막 값을 기준 값으로 정함
g1 = [] # 그룹 1: 기준 값보다 작은 값을 담을 리스트
g2 = [] # 그룹 2: 기준 값보다 큰 값을 담을 리스트
for i in range(0, n - 1): # 마지막 값은 기준 값이므로 제외
if a[i] < pivot: # 기준 값과 비교
g1.append(a[i]) # 작으면 g1에 추가
else:
g2.append(a[i]) # 크면 g2에 추가
# 각 그룹에 대해 재귀 호출로 퀵 정렬을 한 후
# 기준 값과 합쳐 하나의 리스트로 결괏값 반환
return quick_sort(g1) + [pivot] + quick_sort(g2)
d = [6, 8, 3, 9, 10, 1, 2, 4, 7, 5]
print(quick_sort(d))- 실행결과
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]일반적인 퀵 정렬 알고리즘
쉽게 설명한 퀵 정렬 프로그램은 새로운 리스트 g1과 g2를 만들어 값을 분류하고, 결과 리스트도 새로 만들어 돌려줍니다. 이번에는 입력 리스트 안에서 직접 위치를 바꾸면서 정렬하는 일반적인 퀵 정렬을 살펴보겠습니다.
# 퀵 정렬
# 입력: 리스트 a
# 출력: 없음(입력으로 주어진 a가 정렬됨)
# 리스트 a에서 어디부터(start) 어디까지(end)가 정렬 대상인지
# 범위를 지정하여 정렬하는 재귀 호출 함수
def quick_sort_sub(a, start, end):
# 종료 조건: 정렬 대상이 한 개 이하이면 정렬할 필요가 없음
if end - start <= 0:
return
# 기준 값을 정하고 기준 값에 맞춰 리스트 안에서 각 자료의 위치를 맞춤
# [기준 값보다 작은 값들, 기준 값, 기준 값보다 큰 값들]
pivot = a[end] # 편의상 리스트의 마지막 값을 기준 값으로 정함
i = start
for j in range(start, end):
if a[j] <= pivot:
a[i], a[j] = a[j], a[i]
i += 1
a[i], a[end] = a[end], a[i]
# 재귀 호출 부분
quick_sort_sub(a, start, i - 1) # 기준 값보다 작은 그룹을 재귀 호출로 다시 정렬
quick_sort_sub(a, i + 1, end) # 기준 값보다 큰 그룹을 재귀 호출로 다시 정렬
# 리스트 전체(0 ~ len(a) -1)를 대상으로 재귀 호출 함수 호출
def quick_sort(a):
quick_sort_sub(a, 0, len(a) - 1)
d = [6, 8, 3, 9, 10, 1, 2, 4, 7, 5]
quick_sort(d)
print(d)- 실행결과
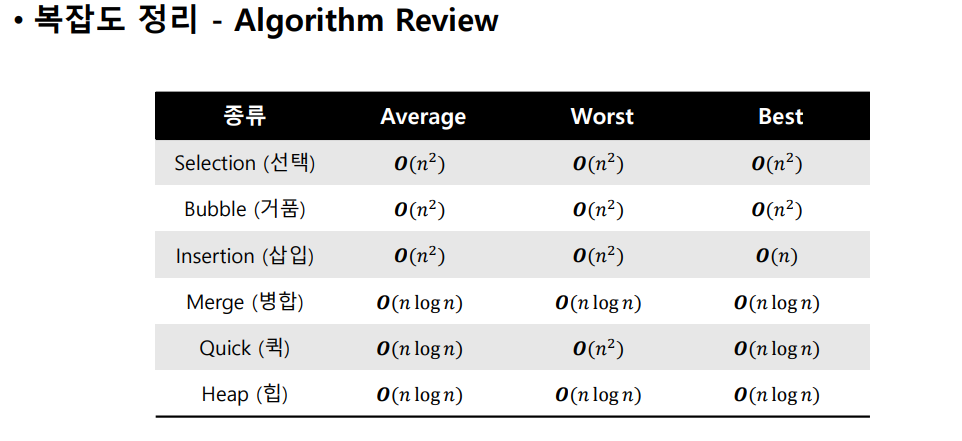
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]복잡도 정리