알고리즘 입문 - 병합 정렬

병합 정렬로 줄 세우기

1 | 학생들에게 일일이 지시하는 것이 귀찮아진 선생님은 학생들이 알아서 줄을 설 수 있는 방법이 없을지 고민입니다. 열 명이나 되는 학생들에게 동시에 알아서 줄을 서라고 하면 너무 소란스러울 것 같아서, 다섯 명씩 두 조로 나누어 그 안에서 키 순서로 줄을 서라고 시켰습니다.

2 | 이제 선생님 앞에는 키 순서대로 정렬된 두 줄(중간 결과 줄)이 있습니다.

3 | 선생님은 각 줄의 맨 앞에 있는 두 학생 중에 키가 더 작은 민수를 뽑아 최종 결과 줄에 세웁니다. 그리고 다시 각 중간 결과 줄의 맨 앞에 있는 두 학생을 비교해 더 작은 학생을 최종 결과 줄의 민수 뒤에 세웁니다.

4| 이 과정을 반복하다가 중간 결과 줄 하나가 사라지면 나머지 중간 결과 줄에 있는 사람을 전부 최종 결과 줄에 세웁니다.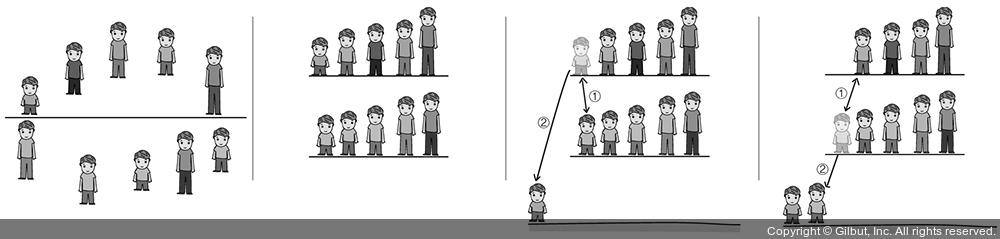

쉽게 설명한 병합 정렬 알고리즘

# 쉽게 설명한 병합 정렬
# 입력: 리스트 a
# 출력: 정렬된 새 리스트

 
def merge_sort(a):
    n = len(a)
    # 종료 조건: 정렬할 리스트의 자료 개수가 한 개 이하이면 정렬할 필요 없음
    if n <= 1:
        return a
    # 그룹을 나누어 각각 병합 정렬을 호출하는 과정
    mid = n // 2              # 중간을 기준으로 두 그룹으로 나눔
    g1 = merge_sort(a[:mid])  # 재귀 호출로 첫 번째 그룹을 정렬
    g2 = merge_sort(a[mid:])  # 재귀 호출로 두 번째 그룹을 정렬
    # 두 그룹을 하나로 병합
    result = []               # 두 그룹을 합쳐 만들 최종 결과
    while g1 and g2:          # 두 그룹에 모두 자료가 남아 있는 동안 반복
        if g1[0] < g2[0]:     # 두 그룹의 맨 앞 자료 값을 비교
            # g1 값이 더 작으면 그 값을 빼내어 결과로 추가
            result.append(g1.pop(0))
        else:
            # g2 값이 더 작으면 그 값을 빼내어 결과로 추가
            result.append(g2.pop(0))
    # 아직 남아 있는 자료들을 결과에 추가
    # g1과 g2 중 이미 빈 것은 while을 바로 지나감
    while g1:
        result.append(g1.pop(0))
    while g2:
        result.append(g2.pop(0))
    return result

 
d = [6, 8, 3, 9, 10, 1, 2, 4, 7, 5] 	
print(merge_sort(d))

• 실행결과

[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

병합 정렬 함수의 첫 부분이 바로 종료 조건입니다.

n = len(a)

if n <= 1:

    return a

입력으로 주어진 리스트 a의 크기가 1 이하이면, 즉 자료가 한 개뿐이거나 아예 비어 있다면 정렬할 필요가 없으므로 입력 리스트를 그대로 돌려주면서 재귀 호출을 끝냅니다.

다음은 전체 리스트를 절반으로 나눠 각각 재귀 호출로 병합 정렬하는 부분입니다.

mid = n // 2             # 두 그룹으로 나누기 위한 중간 값

g1 = merge_sort(a[:mid]) # 재귀 호출로 첫 번째 그룹을 정렬

g2 = merge_sort(a[mid:]) # 재귀 호출로 두 번째 그룹을 정렬

리스트의 자료 개수가 홀수일 때 절반으로 나누는 방법

n // 2는 리스트의 길이 n을 2로 나눈 몫이므로 n이 5와 같은 홀수라면 n // 2는 2가 됩니다. 즉, 자료가 두 개인 그룹과 세 개인 그룹으로 나눕니다.

참고로 a[:mid] 는 리스트 a의 0번 위치부터 mid 위치 직전까지의 자료를 복사해서 새 리스트를 만드는 문장입니다.
또한, a[mid:]는 리스트 a의 mid 위치부터 끝까지의 자료를 복사해서 새 리스트를 만드는 문장입니다.

• Ex

>>> a = [1, 2, 3, 4, 5]
>>> mid = len(a) // 2
>>> mid
2
>>> a[:mid]
[1, 2]
>>> a[mid:]
[3, 4, 5]

병합정렬 단계별 분석

① 숫자 열 개를 두 그룹(g1, g2)으로 나눕니다.

g1: [6 8 3 9 10]
g2: [1 2 4 7 5]

② 두 그룹을 각각 정렬합니다(재귀 호출 부분이므로 이 부분은 뒤에서 설명함. 일단 각 그룹을 정렬해 본다).

g1: [3 6 8 9 10]
g2: [1 2 4 5 7]

③ 이제 두 그룹을 합쳐 다시 한 그룹으로 만들겠습니다(병합).

두 그룹의 첫 번째 값을 비교하여 작은 값을 빼내 결과 리스트에 넣습니다. g1의 첫 번째 값은 3, g2의 첫 번째 값은 1이므로 1을 빼내 결과 리스트(result)에 넣습니다.

g2: [2 4 5 7]
result: [1]

④ 두 그룹의 첫 번째 값을 비교하여 작은 값을 빼내 결과 리스트에 넣는 과정을 반복합니다. 이번에는 g2의 2가 뽑혀 정렬됩니다.

g1: [3 6 8 9 10]
g2: [4 5 7]
result: [1 2]

⑤ 이번에는 g1의 3이 뽑혀 정렬됩니다.

g1: [6 8 9 10]
g2: [4 5 7]
result: [1 2 3]

⑥ 이 과정을 반복하면 다음과 같이 한 그룹의 자료가 다 빠져나가 비어 있게 됩니다.

g1: [8 9 10]
g2: []
result: [1 2 3 4 5 6 7]

⑦ g2에는 자료가 없으므로 비교할 필요 없이 g1에 남아 있는 값을 전부 result로 옮기면 정렬이 끝납니다.

g1: []
g2: []
result: [1 2 3 4 5 6 7 8 9 10]

병합 정렬에서의 재귀 호출

병합 정렬에서 ②번 과정을 보면 두 그룹으로 나눈 자료를 각각 정렬한다. 그렇다면 나누어진 그룹은 어떤 정렬 알고리즘으로 정렬하는 걸까?

바로 병합 정렬이다. 병합 정렬을 하는 과정에서 나누어진 리스트를 다시 두 번의 병합 정렬로 정렬하는 것이다.

이는 원반이 n개인 하노이의 탑 문제를 풀기 위해 원반이 n-1개인 하노이의 탑 문제를 재귀 호출하는 것과 비슷하다.

재귀 호출의 세 가지 요건을 다시 떠올려 보면

1 . 함수 안에서 자기 자신을 다시 호출합니다.
2 . 재귀 호출할 때 인자로 주어지는 입력 크기가 작아집니다.
3 . 특정 종료 조건이 만족되면 재귀 호출을 종료합니다.

병합 정렬은 자료 열 개를 정렬하기 위해 자료를 다섯 개씩 두 그룹으로 나누어 병합 정렬 함수를 재귀 호출한다. 즉, 요건 1, 2는 쉽게 확인할 수 있다.

그렇다면 종료 조건은 병합 정렬의 입력 리스트에 자료가 한 개뿐이거나 아예 자료가 없을 때는 정렬할 필요가 없으므로 입력 리스트를 그대로 돌려주면서 재귀 호출을 끝내면 된다.

일반적인 병합 정렬 알고리즘

정렬 원리는 같지만, return 값이 없고 입력 리스트 안의 자료 순서를 직접 바꾼다는 차이가 있다.

# 병합 정렬
# 입력: 리스트 a
# 출력: 없음(입력으로 주어진 a가 정렬됨)

def merge_sort(a):
    n = len(a)
    # 종료 조건: 정렬할 리스트의 자료 개수가 한 개 이하이면 정렬할 필요가 없음
    if n <= 1:
        return
    # 그룹을 나누어 각각 병합 정렬을 호출하는 과정
    mid = n // 2    # 중간을 기준으로 두 그룹으로 나눔
    g1 = a[:mid]
    g2 = a[mid:]
    merge_sort(g1)  # 재귀 호출로 첫 번째 그룹을 정렬
    merge_sort(g2)  # 재귀 호출로 두 번째 그룹을 정렬
    # 두 그룹을 하나로 병합
    i1 = 0
    i2 = 0
    ia = 0
    while i1 < len(g1) and i2 < len(g2):
        if g1[i1] < g2[i2]:
            a[ia] = g1[i1]
            i1 += 1
            ia += 1
        else:
            a[ia] = g2[i2]
            i2 += 1
            ia += 1 
    # 아직 남아 있는 자료들을 결과에 추가
    while i1 < len(g1):
        a[ia] = g1[i1]
        i1+= 1
        ia += 1
    while i2 < len(g2):
        a[ia] = g2[i2]
        i2 += 1
        ia += 1

d = [6, 8, 3, 9, 10, 1, 2, 4, 7, 5]
merge_sort(d)
print(d)

• 실행결과

[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

• 예시
  

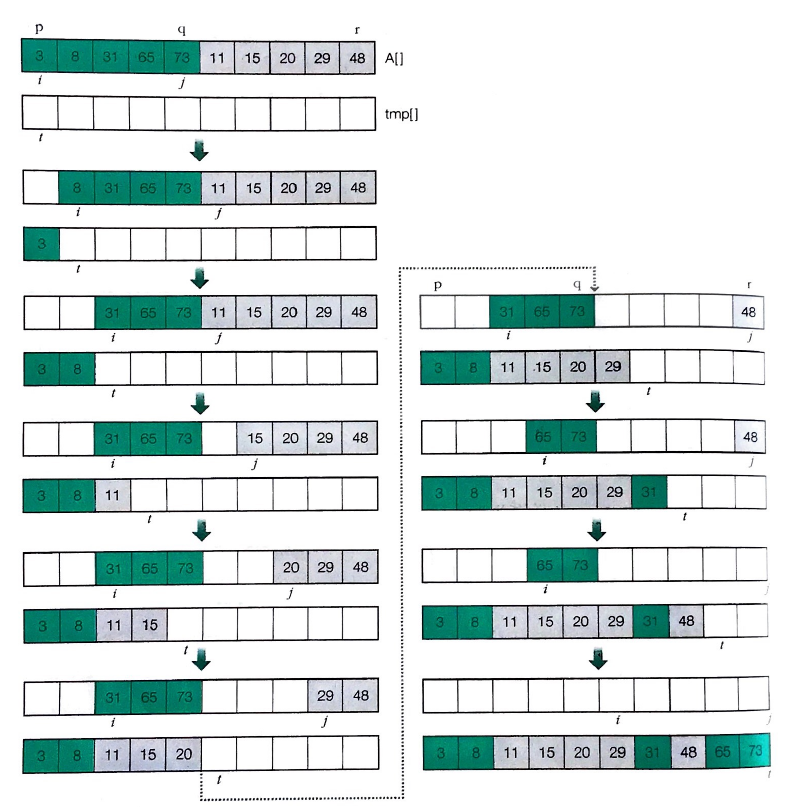
알고리즘 분석

병합 정렬은 주어진 문제를 절반으로 나눈 다음 각각을 재귀 호출로 풀어 가는 방식이다.

이처럼 큰 문제를 작은 문제로 나눠서(분할하여) 푸는(정복하는) 방법을 알고리즘 설계 기법에서는 ‘분할 정복(divide and conquer)’이라고 부른다.

입력 크기가 커서 풀기 어려웠던 문제도 반복해서 잘게 나누다 보면 굉장히 쉬운 문제(종료 조건)가 되는 원리를 이용한 것이다. 분할 정복은 잘 활용하면 계산 복잡도가 더 낮은 효율적인 알고리즘을 만드는 데 도움이 된다.

분할 정복을 이용한 병합 정렬의 계산 복잡도는 O(n·logn)으로 선택 정렬이나 삽입 정렬의 계산 복잡도 O(n제곱)보다 낮다. 따라서 정렬해야 할 자료의 개수가 많을수록 병합 정렬이 선택 정렬이나 삽입 정렬보다 훨씬 더 빠른 정렬 성능을 발휘한다.

예를 들어 대한민국 국민 오천만 명을 생년월일 순서로 정렬한다고 생각해 보면 입력 크기가 n = 50,000,000일 때 n제곱은 2,500조이고 n·log n은 약 13억이다. 2,500조는 13억보다 무려 200만 배 정도 큰 숫자이다. 이 사실을 알면 O(n2) 정렬 알고리즘과 O(n·logn) 정렬 알고리즘의 계산 시간이 얼마나 많이 차이 나는지 짐작할 수 있을 것이다.

내림차순 정렬

오름차순 정렬에서 값을 비교하는 부분(g1[i1] < g2[i2])의 부등호 방향을 반대로 하면 내림차순 정렬 프로그램이 된다.

# 내림차순 병합 정렬
# 입력: 리스트 a
# 출력: 없음(입력으로 주어진 a가 정렬됨)


def merge_sort(a):
    n = len(a)
    # 종료 조건: 정렬할 리스트의 자료 개수가 한 개 이하이면 정렬할 필요가 없음
    if n <= 1:
        return
    # 그룹을 나누어 각각 병합 정렬을 호출하는 과정
    mid = n // 2
    g1 = a[:mid]
    g2 = a[mid:]
    merge_sort(g1)
    merge_sort(g2)
    # 두 그룹을 합치는 과정(병합)
    i1 = 0
    i2 = 0
    ia = 0
    while i1 < len(g1) and i2 < len(g2):
        if g1[i1] > g2[i2]: # 부등호 방향 뒤집기
            a[ia] = g1[i1]
            i1 += 1
            ia += 1
        else:
            a[ia] = g2[i2]
            i2 += 1
            ia += 1
    while i1 < len(g1):
        a[ia] = g1[i1]
        i1 += 1
        ia += 1
    while i2 < len(g2):
        a[ia] = g2[i2]
        i2 += 1
        ia += 1
 
d = [6, 8, 3, 9, 10, 1, 2, 4, 7, 5]
merge_sort(d)
print(d)