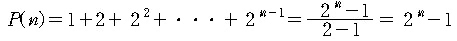원반이 n개인 하노이의 탑을 옮기기 위한 원반 이동 순서를 출력하는 알고리즘
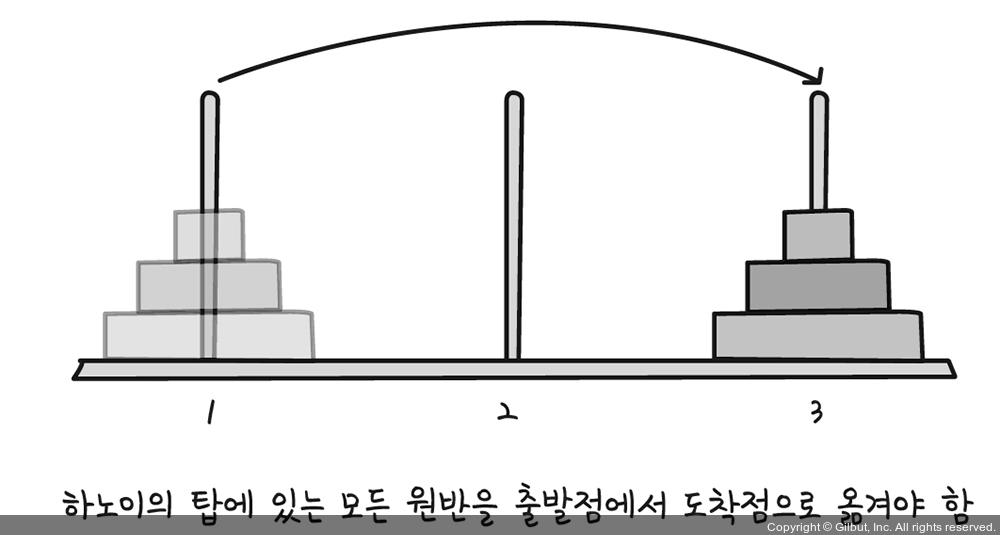
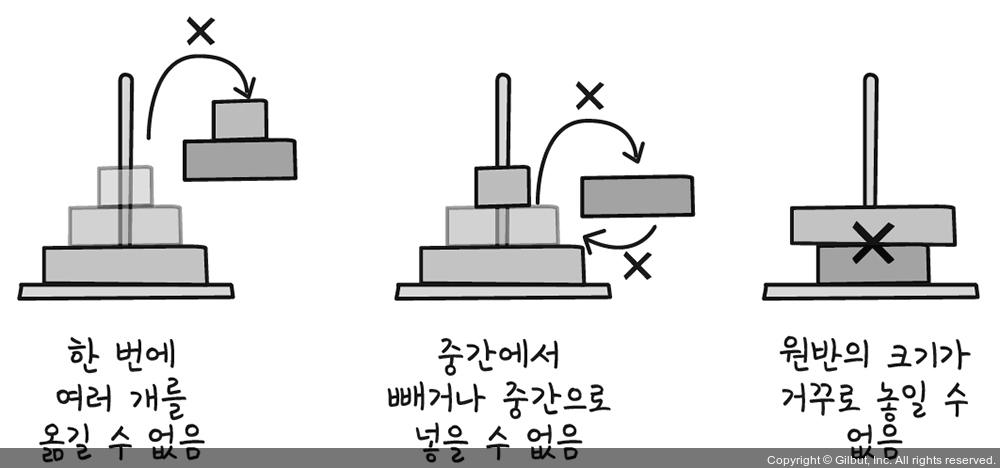
하노이의 탑 규칙
• 크기가 다른 원반 n개를 출발점 기둥에서 도착점 기둥으로 전부 옮겨야 합니다.
• 원반은 한 번에 한 개씩만 옮길 수 있습니다.
• 원반을 옮길 때는 한 기둥의 맨 위 원반을 뽑아, 다른 기둥의 맨 위로만 옮길 수 있습니다(기둥의 중간에서 원반을 빼내거나 빼낸 원반을 다른 기둥의 중간으로 끼워 넣을 수 없습니다).
• 원반을 옮기는 과정에서 큰 원반을 작은 원반 위로 올릴 수 없습니다.
하노이의 탑 풀이
- 원반이 한 개일 때 (1번 걸림)
1번 기둥에 있는 원반을 3번 기둥으로 옮기면 끝난다.(1 → 3)
- 원반이 두 개일 때 (3번 걸림)
1번 기둥의 맨 위에 있는 원반을 2번 기둥으로 옮긴다.(1 → 2)
1번 기둥에 남아 있는 큰 원반을 3번 기둥으로 옮긴다.(1 → 3)
2번 기둥에 남아 있는 원반을 3번 기둥으로 옮긴다.(2 → 3) - 원반이 세 개일 때 (3+1+3 = 7번 걸림)
하노이의 탑 규칙에 따르면 한 번에 원반을 두 개씩 옮길 수 없다고 했지만, 우리는 이미 원반이 두 개일 때 하노이의 탑을 푸는 방법을 알고 있으니 그 방법을 그대로 적용하면 된다.1번 기둥에 있는 원반 세 개 중에 위에 있는 원반 두 개를 비어 있는 2번 기둥(보조 기둥)으로 옮긴다. (1 → 3, 1 → 2, 3 → 2) 실제로 원반은 세번 이동함
1번 기중에 남아 있는 큰 원반을 3번 기둥으로 옮긴다.(1 → 3)
이번에는 2번 기둥에 있는 원반 두 개를 3번 기둥으로 옮긴다.(2 → 1, 2 → 3, 1 → 3) 실제로 원반은 세번 이동함
n번으로 일반화해보기 >> 재귀호출 사용 가능
- 원반이 n개일 때
- 1번 기둥에 있는 n-1개 원반을 2번 기둥으로 옮깁니다(n-1개짜리 하노이의 탑 문제 풀기).
- 1번 기둥에 남아 있는 가장 큰 원반을 3번 기둥으로 옮깁니다(1 → 3).
- 2번 기둥에 있는 n-1개 원반을 3번 기둥으로 옮깁니다(n-1개짜리 하노이의 탑 문제 풀기).
원반이 한 개면 그냥 옮기면 끝(종료 조건)
하노이의 탑 알고리즘
원반이 한 개일 때가 바로 ‘종료 조건’에 해당한다. 원반 n개 문제를 풀려면 n-1개 원반 문제를 풀어야 하는데, 이는 바로 ‘좀 더 작은 값으로 자기 자신을 호출’하는 과정이다. 따라서 이 문제는 전형적인 재귀 호출 알고리즘에 해당한다.
# 하노이의 탑
# 입력: 옮기려는 원반의 개수 n
# 옮길 원반이 현재 있는 출발점 기둥 from_pos
# 원반을 옮길 도착점 기둥 to_pos
# 옮기는 과정에서 사용할 보조 기둥 aux_pos
# 출력: 원반을 옮기는 순서
def hanoi(n, from_pos, to_pos, aux_pos):
if n == 1: # 원반 한 개를 옮기는 문제면 그냥 옮기면 됨
print(from_pos, ”->“, to_pos)
return
# 원반 n -1개를 aux_pos로 이동(to_pos를 보조 기둥으로)
hanoi(n -1, from_pos, aux_pos, to_pos)
# 가장 큰 원반을 목적지로 이동
print(from_pos, ”->“, to_pos)
# aux_pos에 있는 원반 n -1개를 목적지로 이동(from_pos를 보조 기둥으로)
hanoi(n - 1, aux_pos, to_pos, from_pos)
print(“n = 1”)
hanoi(1, 1, 3, 2) # 원반 한 개를 1번 기둥에서 3번 기둥으로 이동(2번을 보조 기둥으로)
print(“n = 2”)
hanoi(2, 1, 3, 2) # 원반 두 개를 1번 기둥에서 3번 기둥으로 이동(2번을 보조 기둥으로)
print(“n = 3”)
hanoi(3, 1, 3, 2) # 원반 세 개를 1번 기둥에서 3번 기둥으로 이동(2번을 보조 기둥으로)- 실행 결과
n = 1 # hanoi(1, 1, 3, 2)
1 -> 3 # print(1,”->“,3)
n = 2 # hanoi(2, 1, 3, 2)
1 -> 2 # hanoi(1, 1, 2, 3)
1 -> 3 # print(1,”->“,3)
2 -> 3 # hanoi(1, 2, 3, 1)
n = 3
1 -> 3
1 -> 2
3 -> 2
1 -> 3
2 -> 1
2 -> 3
1 -> 3알고리즘 분석
입력 크기, 즉 탑의 층수가 높을수록 원반을 더 많이 움직여야 한다.
n층짜리 하노이의 탑을 옮기려면 원반을 모두 (2n승-1)번 옮겨야 한다. 마찬가지로 n이 커지면 -1은 큰 의미가 없으므로 O(2n)으로 표현할 수 있다. 이는 2를 n번 제곱한 값이므로 n이 커짐에 따라 값이 기하급수적으로 증가한다.
이동횟수: 2 x H(n-1) + 1
H(n) = 2H(n-1) + 1
H(1) = 1
H(2) = 2 H(1) + 1 = 2 + 1 = 3
H(3) = 2 H(2) + 1 = 2 x 3 + 1 = 4(2의 2승) + 2 + 1 = 7
H(4) = 2 H(3) + 1 = 2 x 7 + 1 = 8(2의 3승) + 4(2의 2승) + 2 + 1 = 15 ...
- 등비수열의 합 공식 이용