
⭐️ 그래프란?
그래프는 연결되어 있는 원소간의 관계를 표현한 자료구조이다.
그래프는 노드(N, node)와 그 노드를 연결하는 간선(E, edge)의 집합으로 구성된다.
- 즉, 연결되어 있는 객체 간의 관계를 표현할 수 있는 자료 구조이다.
- ex) 철도망의 안정성 분석, 소셜 네트워크 분석, 인터넷 전송 속도 계산, 한 붓 그리기, 외한 거래 등
- 그래프는 여러 개의 고립된 부분 그래프로 구성될 수 있다.
- 그래프는 주로 연결 관계를 표현하기 위해 사용된다.
이러한 그래프를 저장하는 3가지가 있다.
1️⃣ 인접 행렬 (Adjacency Matrix)
인접 행렬이란, 그래프의 연결 관계를 행렬로 표현하여 이차원 배열로 나타내는 방식을 의미한다.
adj[i][j] : 노드 i에서 j로 가는 간선이 존재할 경우 1, 아니면 0
만약 표현하고자 하는 그래프가 방향이 없는 무향 그래프의 경우 노드 i에서 노드 j로 가는 길이 존재하면 노드 j에서 노드 i로 가는 길 또한 존재한다.
이러한 특성으로 인접 행렬을 구현할 경우, 대각 성분을 기준으로 대칭인 성질을 가지게 된다.
- 2차원 배열을 활용하여 그래프를 표현하는 방식
👇 인접 행렬의 가중치가 있는 방향 그래프
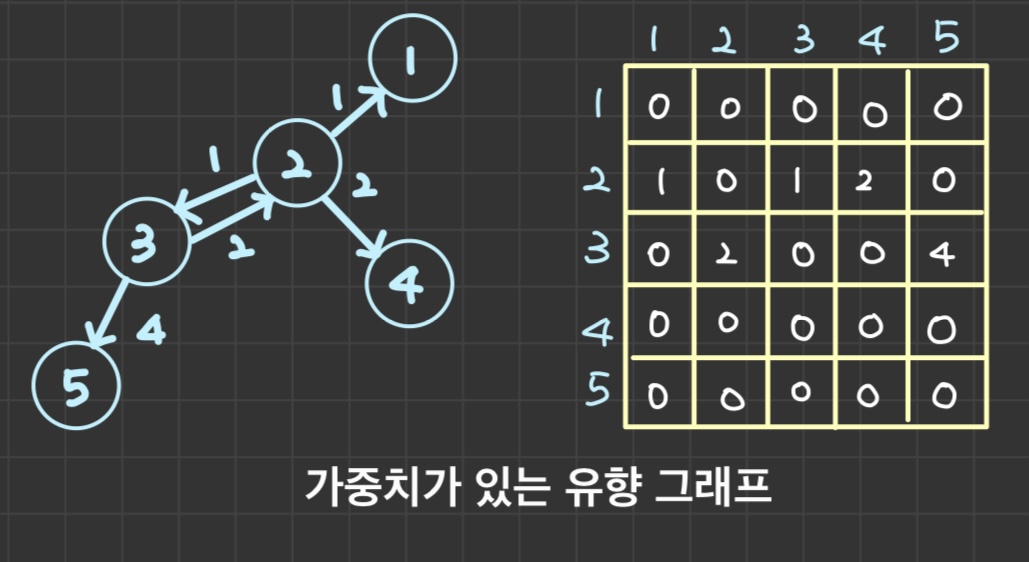
👇 인접 행렬의 가중치가 없는 무방향 그래프
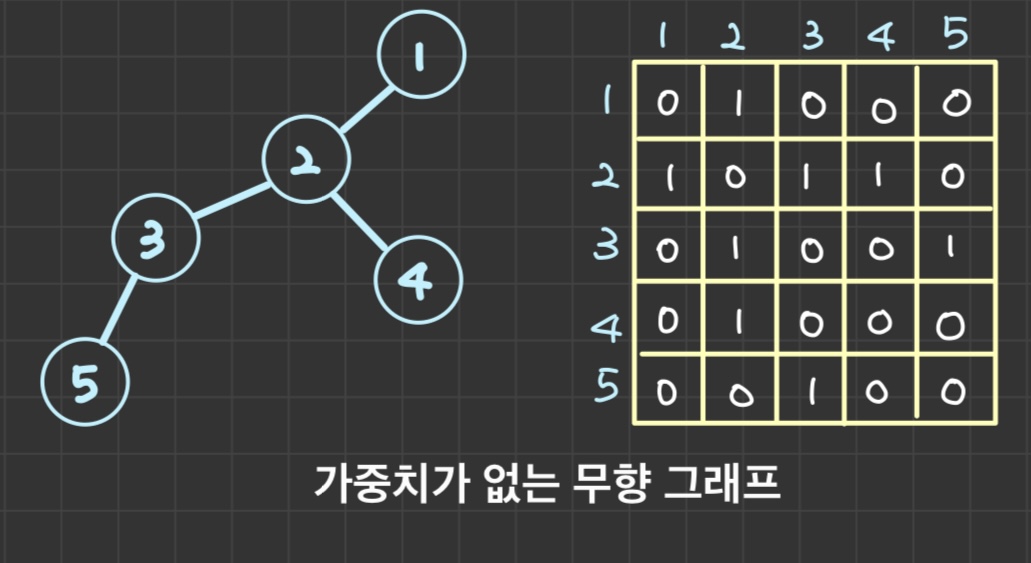
💻 인접 행렬 (방향 그래프) 구현
V, E = 6, 8
edge = [0, 1, 0, 2, 0, 5, 0, 6, 4, 3, 5, 3, 5, 4, 6, 4]
adj_matrix = [[0]*(V+1) for _ in range(V+1)]
for i in range(E):
# 2*i와 2*i+1은 edge 리스트에서 간선 정보를 가져오기 위한 인덱스
num1, num2 = edge[2*i], edge[2*i+1]
# num1 정점에서 num2 정점으로의 방향성을 가진 간선이 존재함을 나타냄
adj_matrix[num1][num2] = 1💻 인접 행렬 (무방향 그래프) 구현
V, E = 6, 8
edge = [0, 1, 0, 2, 0, 5, 0, 6, 4, 3, 5, 3, 5, 4, 6, 4]
adj_matrix = [[0]*(V+1) for _ in range(V+1)]
for i in range(E):
# 2*i와 2*i+1은 edge 리스트에서 간선 정보를 가져오기 위한 인덱스
num1, num2 = edge[2*i], edge[2*i+1]
# 각 인덱스에 1을 할당하여 num1과 num2 사이에 간선의 존재 여부를 나타냄
adj_matrix[num1][num2] = 1
adj_matrix[num2][num1] = 1🟢 인접 행렬의 장점
- 구현이 쉽다
- 노드 i와 노드 j가 연결되어 있는지 확인하고 싶을 때, indexing으로 접근하기 때문에 O(1)의 시간 복잡도를 가진다.
🔴 인접 행렬의 단점
- 전체 노드의 개수를 v개, 간선의 개수를 E개라고 하면, 노드 i에 연결된 모든 노드들에 방문하고 싶은 경우 adj[i][1]부터 adj[i][V]를 모두 확인해봐야 하기 때문에 총 O(V)의 시간이 걸린다.
- 노드의 수에 비해 간선의 개수가 훨씬 적은 그래프면 적절하지 않다.
2️⃣ 인접 리스트 (Adjacency List)
인접 리스트란, 각각의 노드에 연결된 노드들을 원소로 갖는 리스트들의 배열을 의미한다.
adj[i] : i번째 노드에 연결된 노드들을 원소로 갖는 리스트
인접 리스트 또한 무방향 그래프의 경우에는 본인 노드 인덱스의 리스트 내에 서로를 원소로 가지게 된다.
- 인접 리스트를 활용하여 표현하는 방식
- 인접 리스트는 그래프의 전체 노드 목록을 저장한다.
- Python에서는 하나의 노드가 키(key)가 되고, 그 노드에 인접한 노드가 값(value)이 되는 딕셔너리로 구현할 수 있다.
- 인접 리스트는 인접 행렬이 갖는 단점을 극복할 수 있다.
👇 인접 리스트의 가중치가 있는 방향 그래프
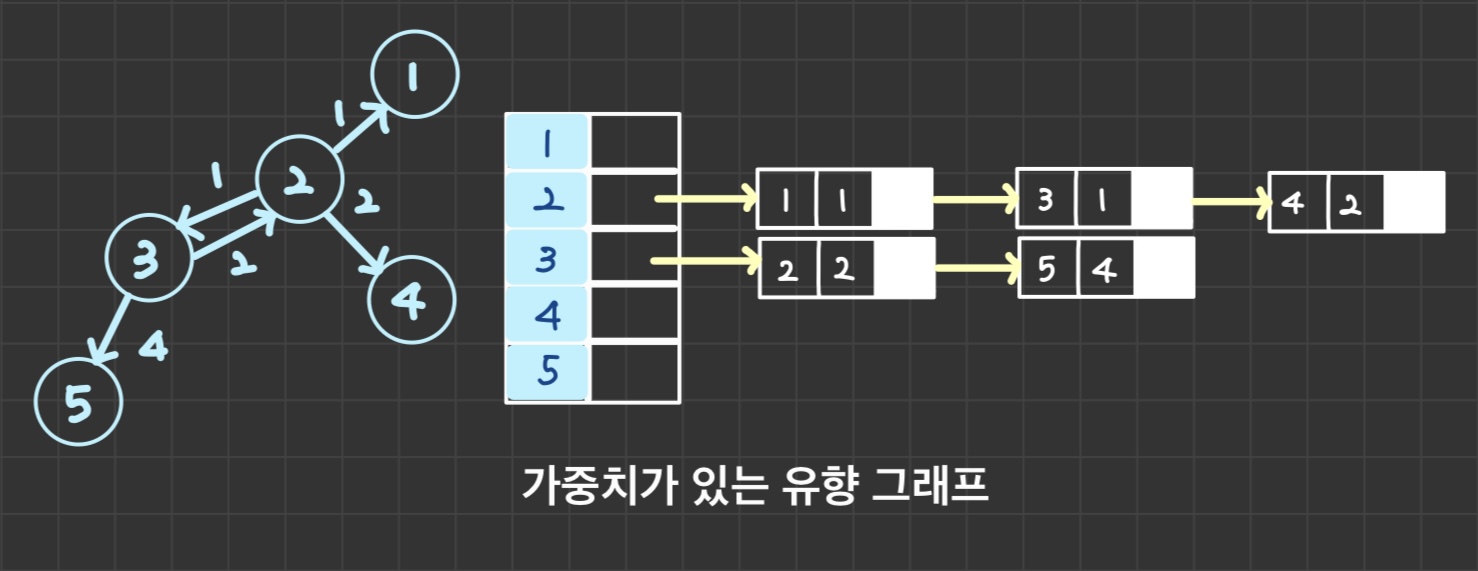
👇 인접 리스트의 가중치가 없는 무방향 그래프
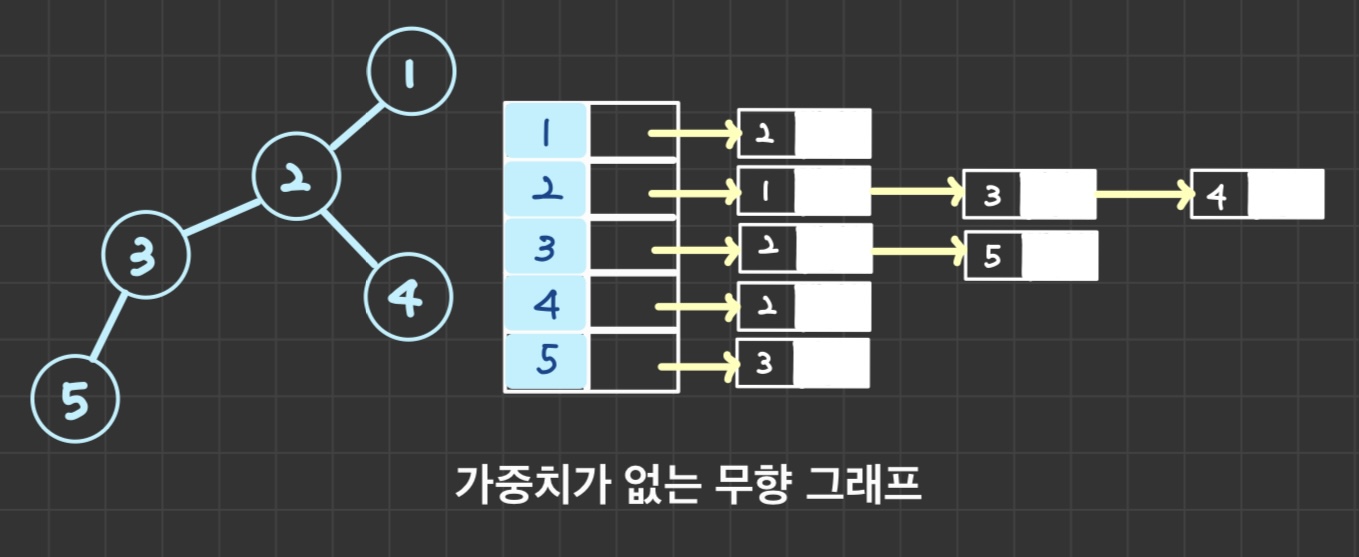
💻 인접 리스트 (방향 그래프) 구현
V, E = 6, 8
edge = [0, 1, 0, 2, 0, 5, 0, 6, 4, 3, 5, 3, 5, 4, 6, 4]
# 인접 리스트를 생성하여 각 정점에 연결된 간선 정보를 저장할 배열
adj_list = [[] for _ in range(V+1)]
for i in range(E):
# 현재 간선을 구성하는 시작 정점과 끝 정점을 num1, num2 변수에 할당
# 2*i와 2*i+1은 edge 리스트에서 간선 정보를 가져오기 위한 인덱스
num1, num2 = edge[2*i], edge[2*i+1]
# num1 정점에 연결된 간선의 끝 정점 num2를 adj_list 리스트에 추가
# num1 정점과 num2 정점이 방향성을 가진 간선으로 연결되어 있다는 정보를 인접 리스트에 저장
adj_list[num1].append(num2)💻 인접 리스트 (무방향 그래프) 구현
V, E = 6, 8
edge = [0, 1, 0, 2, 0, 5, 0, 6, 4, 3, 5, 3, 5, 4, 6, 4]
# 인접 리스트를 생성하여 각 정점에 연결된 간선 정보를 저장할 배열
adj_list = [[] for _ in range(V+1)]
for i in range(E):
# 현재 간선을 구성하는 시작 정점과 끝 정점을 num1, num2 변수에 할당
# 이때 2*i와 2*i+1은 edge 리스트에서 간선 정보를 가져오기 위한 인덱스
num1, num2 = edge[2*i], edge[2*i+1]
# num1 정점에 연결된 간선의 끝 정점 num2를 adj_list에 추가
# 이것은 num1 정점과 num2 정점이 연결되어 있다는 정보를 인접 리스트에 저장하는 것을 의미
adj_list[num1].append(num2)
# 무방향 그래프이기 때문에 num2 정점에도 num1 정점을 연결된 간선의 끝 정점으로 추가
# 이것은 num2 정점과 num1 정점이 연결되어 있다는 정보를 인접 리스트에 저장하는 것을 의미
adj_list[num2].append(num1)🟢 인접 리스트의 장점
- 실제 연결된 노드에 대한 정보만 저장하기 때문에, 모든 원소의 개수의 합이 간선의 개수와 동일하다.
- 즉, 간선의 개수에 비례하는 메모리만 차지하여 구현이 가능하다.
- 각 노드에 연결된 모든 노드들을 방문해 보아야 하는 경우, 인접 리스트로 연결 관계를 저장하는 것이 시간상 큰 이점을 가진다.
🔴 인접 리스트의 단점
- 노드 i와 j의 연결 여부를 알고 싶을 때, adj[i] 리스트를 순회하며 j 원소가 존재하는지 확인해야 한다 → 시간 복잡도 O(V)
- 인접 행렬은 adj[i][j]가 1인지 0인지만 확인하면 i와 v 노드의 연결 여부를 O(1)로 확인 가능하다.
3️⃣ 간선 리스트 (Edge List)
간선 리스트는 인접 리스트와 인접 행렬을 모두 사용할 수 없는 경우에 간선 리스트를 사용한다.
STL, Array, collection 등을 사용할 수 없는 경우에 해당된다.
하나의 배열을 이용하여 모든 간선은 저장하고, 누적합을 저장한 다른 배열로 한 정점의 간선이 저장된 index의 범위를 알려주도록 한다.
- 그래프를 정점, 간선 두 가지 요소로 분리하여 사용한다.
- 간선 리스트는 간선을 모두 저장하고 있다.
- 간선 리스트는 [노드1 혹은 출발 노드, 노드2 혹은 도착 노드, 가중치] 형태의 자료구조를 리스트 또는 배열의 형태로 저장하는 방식이다.
👇 간선 리스트의 그래프
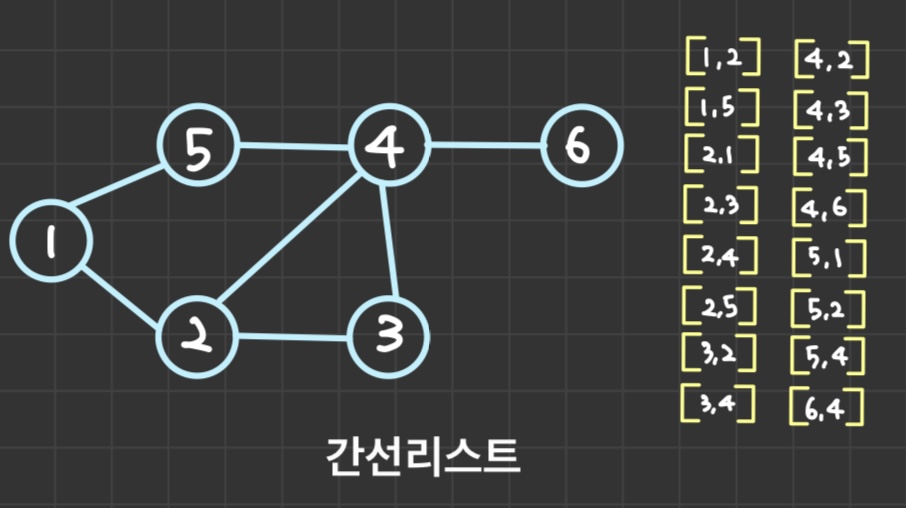
💻 간선 리스트 (방향 그래프) 구현
V = 7
edge = [(1, 2), (1, 5), (2, 1), (2, 3), (2, 4), (2, 5), (3, 2), (3, 4), (3, 4), (4, 2), (4, 3), (4, 5), (4, 6), (5, 1), (5, 2), (5, 4), (6, 4)]
agj_list = [[] for _ in range(V)]
for u, v in edge:
# 시작 정점 u와 끝 정점 v를 추출하여 adj_list에 각각의 정점을 연결
# 방향 그래프이므로 u 정점에 v를 추가
adj_list[u].append(v)💻 간선 리스트 (무방향 그래프) 구현
V = 7
edge = [(1, 2), (1, 5), (2, 1), (2, 3), (2, 4), (2, 5), (3, 2), (3, 4), (3, 4), (4, 2), (4, 3), (4, 5), (4, 6), (5, 1), (5, 2), (5, 4), (6, 4)]
agj_list = [[] for _ in range(V)]
for u, v in edge:
# 시작 정점 u와 끝 정점 v를 추출하여 adj_list에 각각의 정점을 연결
# 무방향 그래프이므로 u 정점에 v를, v 정점에 u를 추가
adj_list[u].append(v)
adj_list[v].append(u)🟢 간선 리스트의 장점
- 구현이 가장 간단하다.
- 모든 간선을 탐색할 때 유리하다 (ex) 벨만-포드 알고리즘
🔴 간선 리스트의 단점
- 특정 두 노드가 이웃한지 알아보려면 모든 간선을 탐색해야 한다.
- 특정 노드에 연결된 간선을 알아보려면 모든 간선을 탐색해야 한다.
Reference
(책) 프로그래밍 대회에서 배우는 알고리즘 문제해결전략
https://ninefloor-design.tistory.com/165
https://livecoding.tistory.com/49
https://ko.wikipedia.org/wiki/%EC%9D%B8%EC%A0%91%ED%96%89%EB%A0%AC
https://ko.wikipedia.org/wiki/%EC%9D%B8%EC%A0%91_%EB%A6%AC%EC%8A%A4%ED%8A%B8

안녕하세요
간선 리스트에서 [2, 5]는 왜 들어가는건가요?