🔍 스택(Stack)이란?
💡 스택(Stack)은 한 쪽 끝에서만 제한적으로 접근하여 데이터를 넣고 뺄 수 있는 후입선출(Last-In-First-Out) 형태의 선형 자료구조이다.
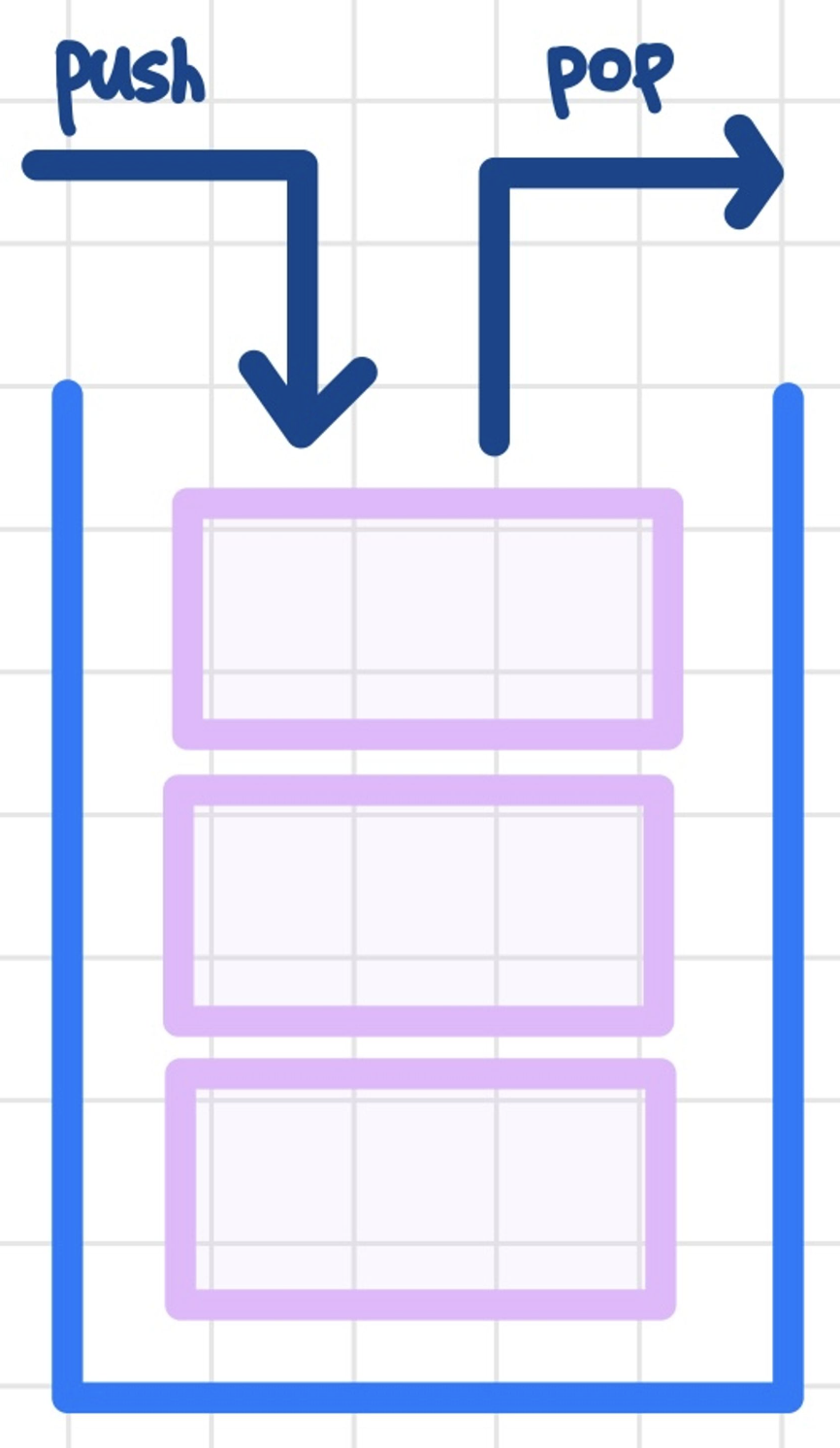
스택(Stack)은 LIFO(Last-In-First-Out)/FILO(First-In-Last-Out) 순서를 따른다.
- LIFO(Last-In-First-Out): 마지막에 들어온 값이 처음으로 나가는 것
- FILO(First-In-Last-Out): 처음 들어온 값이 마지막에 나가는 것
기본적으로 stack 클래스는 내부에서 최상위 타입 배열인 Object[] 배열을 사용하여 데이터를 관리하고 있다.
👉 스택(Stack)의 특징
- 스택 내부의 데이터는 top을 통해서만 접근할 수 있다.
- top은 가장 마지막에 들어온 데이터를 의미한다.
- 스택에 데이터를 삽입할 때는 top 위에 삽입 → push 연산
- 스택에서 데이터를 삭제할 때는 top에 위치한 데이터를 삭제 → pop 연산
→ 스택은 시간 순서에 따라 데이터가 쌓이게 되므로 가장 마지막에 삽입된 데이터가 가장 먼저 삭제된다는 특징을 가진다.
- 이러한 스택의 구조를 후입선출 구조하고 한다.
🔄 스택(Stack)의 작동원리
스택은 기본적으로 후입선출(나중에 들어온 데이터가 가장 먼저 나가는) 구조로 이루어져 있다.
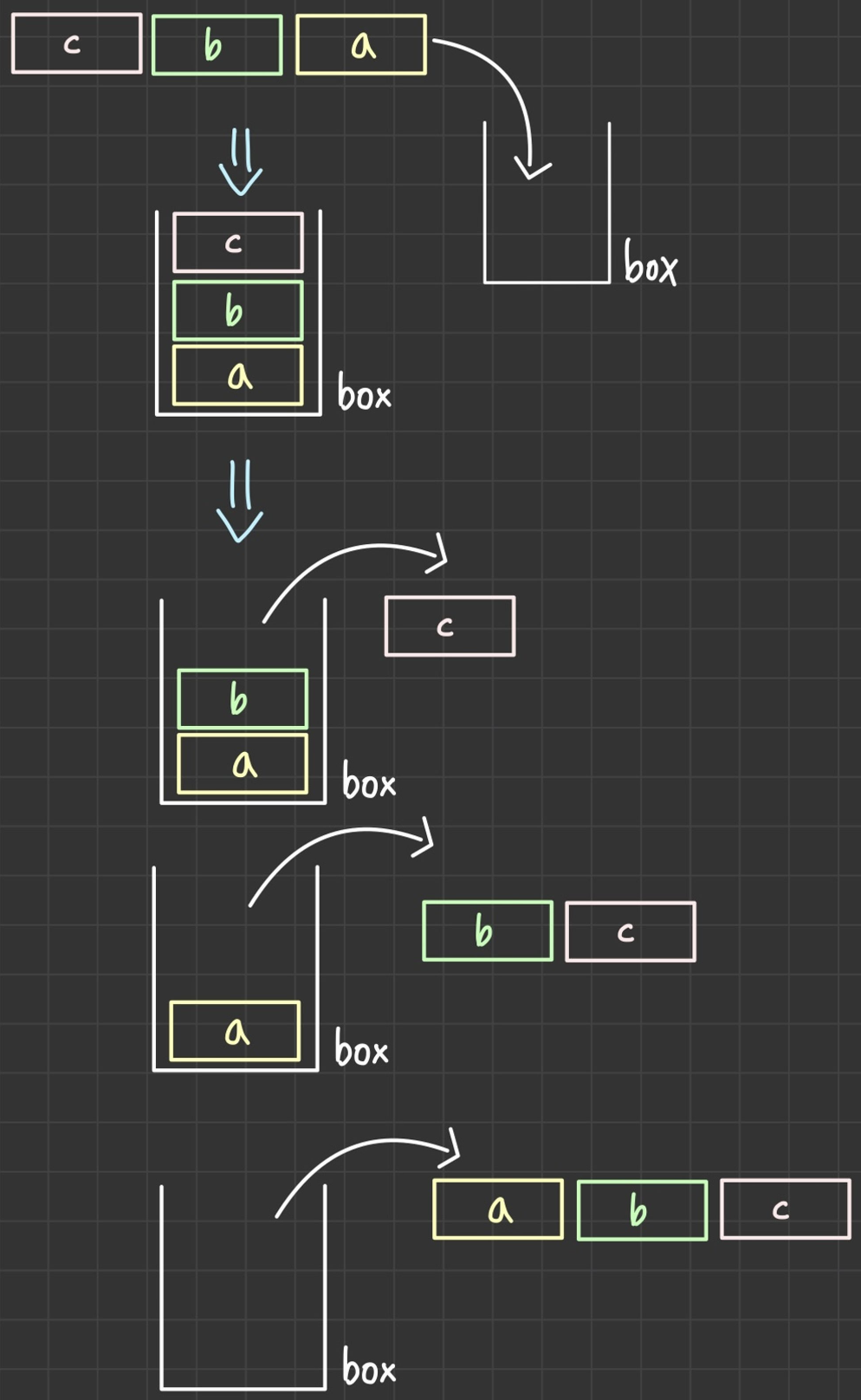
위의 그림을 보면 가장 먼저 들어온 a 데이터가 가장 마지막에 쌓여있고 가장 나중에 들어온 c 데이터가 가장 위에 놓여져 있다. 데이터를 넣고 빼는 입구가 하나뿐인 스택은 가장 위에 쌓인 데이터를 먼저 꺼내도록 작동한다.
📝 스택(Stack)의 연산
✔️ 가장 최근에 스택에 추가한 항목이 가장 먼저 제거될 항목
- pop() : 스택에서 가장 위에 있는 항목을 제거한다.
- push(item) : item 하나를 스택의 가장 윗 부분에 추가한다.
- peek() : 스택의 가장 위에 있는 항목을 반환한다.
- isEmpty() : 스택이 비어 있을 때 true를 반환한다.
🌐 스택(Stack)의 구조
스택은 아래 그림과 같은 구조로 이루어져 있다.
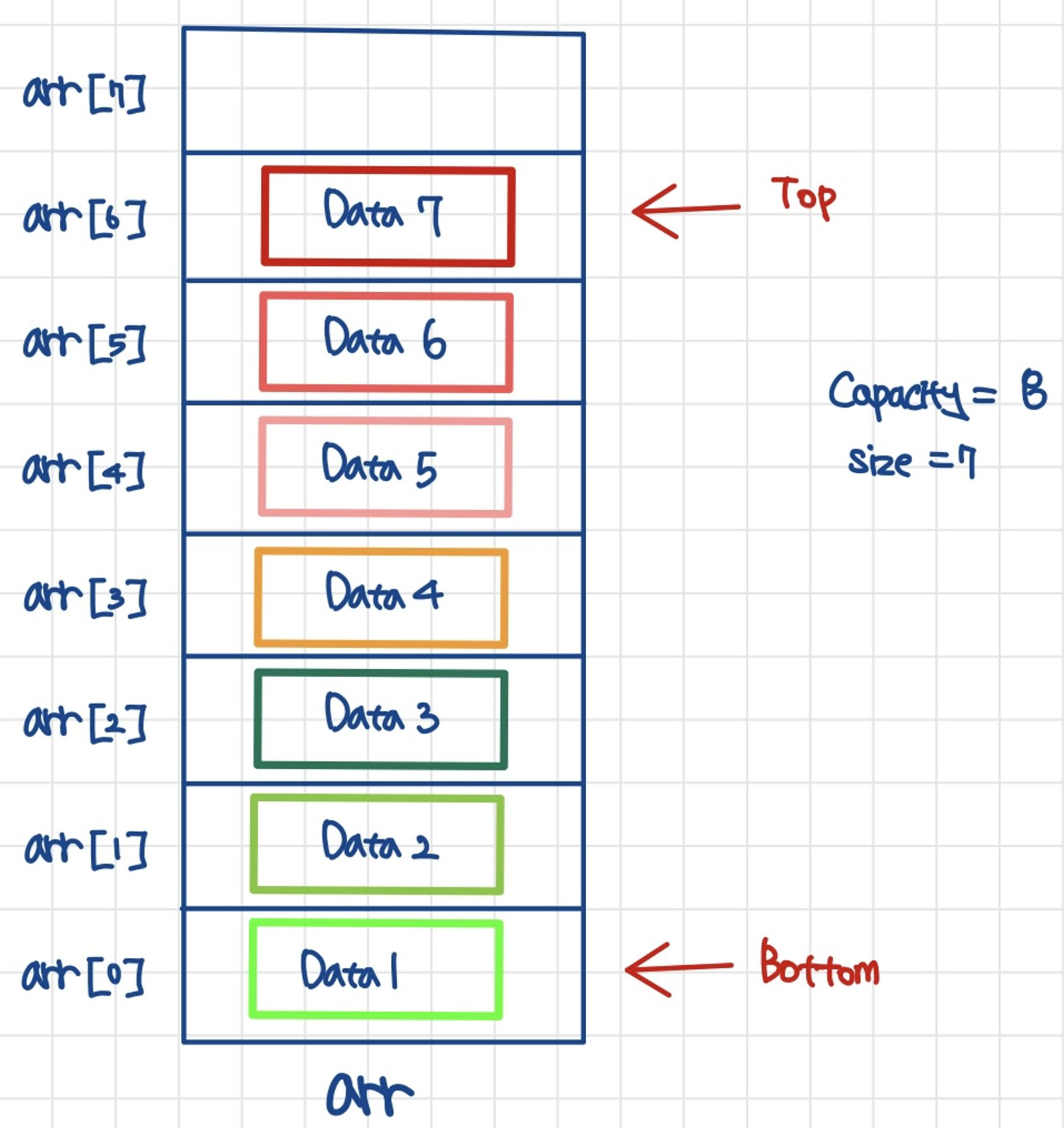
Bottom: 가장 밑에 있는 데이터 또는 인덱스
Top: 가장 위에 있는 데이터 또는 인덱스
Capacity: 스택에 담을 수 있는 데이터의 총 용량
Size: 현재 스택에 담겨져있는 데이터의 개수
🔡 스택(Stack) 구현
문제의 종류에 따라 배열보다 스택에 데이터를 저장하는 것이 더 적합한 방법일 수 있다.
- 배열과 달리 스택은 상수 시간에 i번째 항목에 접근할 수 없다.
- 하지만 스택에서 데이터를 추가하거나 삭제하는 연산은 상수 시간에 가능하다.
- 배열처럼 원소들을 하나씩 옆으로 밀어 줄 필요가 없다.
스택은 연결리스트로 구현할 수 있다. 연결리스트의 같은 방향에서 아이템을 추가하고 삭제하도록 구현한다.
class stack:
def __init__(self): # stack 객체 생성
self.items = []
def push(self, data): # stack 데이터 추가 append
self.items.append(data)
def pop(self):
pop_object = None
if self.isEmpty():
print("Stack is Empty")
else:
pop_object = self.items.pop()
return pop_object # stack의 가장 마지막 데이터를 삭제하고 return pop()
def peek(self):
if self.isEmpty():
print("Stack is Empty")
else:
return self.top[-1]
return top_object # stack의 가장 마지맏 데이터 return
def isEmpty(self):
is_empty = False
if len(self.items) == 0:
is_empty = True
return is_empty # stack이 비었는지 확인하고 boolean 값으로 반환1️⃣ 데이터 추가 - push ()
💡 스택에 데이터를 추가하는 작업은 push()로 이루어진다.
스택에 데이터를 추가하면 가장 마지막 부분(최상단)에 추가된다. 스택에 데이터를 추가하는 push 작업은 인덱스를 증가하면서 이루어진다.
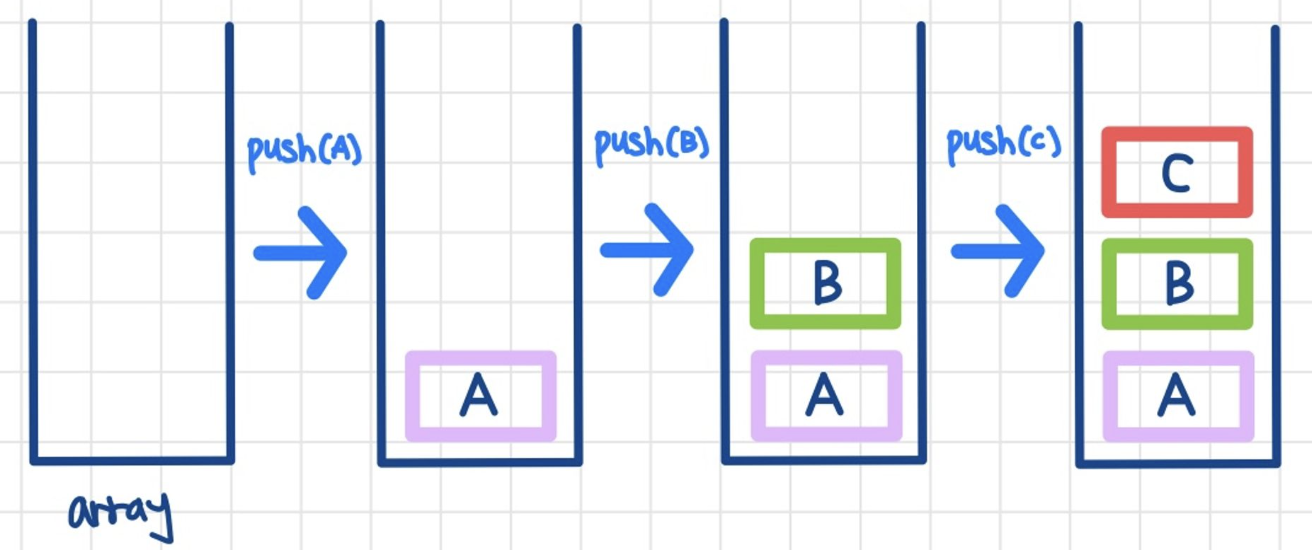
- 1단계: 스택이 가득 차 있는 확인
- 2단계: 스택이 가득 차 있으면 오류 발생 및 종료
- 3 단계: 스택이 가득 차 있는 상태가 아니면 Top을 증가
- 4 단계: Top이 가리키는 스택 위치에 데이터를 추가
array = list()
def append(data):
array.append(data)
append("A")
append("B")
append("C")2️⃣ 데이터 삭제 - pop()
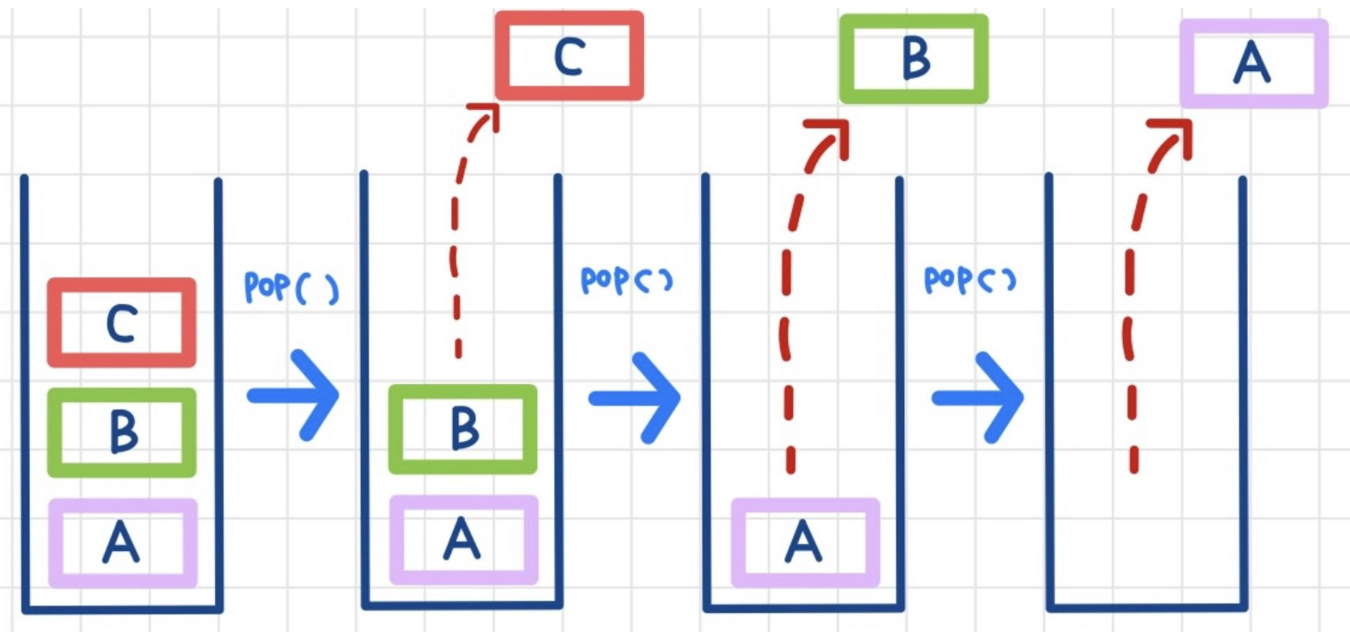
💡 스택에 데이터를 삭제하는 작업은 pop()으로 이루어진다.
스택에 데이터를 삭제하는 작업은 가장 위에 있는 (가장 마지막에 추가된 데이터) 데이터를 제거한다.
- 1 단계: 스택이 비어 있는지 확인
- 2 단계: 스택이 비어 있으면 오류 발생 및 종료
- 3 단계: 스택이 비어 있지 않으면 Top이 가리는 데이터를 제거
- 4 단계: Top 값을 제거
데이터 제거 시 중요한 점은 스택이 비어있어 삭제할 데이터가 없는 경우이다.
array = list()
def pop():
data = array[-1]
def array[-1]
return data
pop() # C
pop() # B
pop() # A3️⃣ 최상단 데이터 확인 - peek()
💡 peek()은 가장 상단에 있는 데이터를 삭제하지 않고 확인만 하고 싶을 때 사용하는 메서드이다.
스택의 가장 위에 있는 항목을 반환하며 pop()에서 삭제 과정만 없는 것이 peek()이다.
4️⃣ 데이터 유무 확인 - isEmpty()
💡 isEmpty() 는 Stack이 비어있는지 확인하는 메서드이다.
스택이 비어 있으면 True, 데이터가 있으면 False를 반환한다.
⌛️ 스택(Stack) 시간복잡도
💡 스택은 상수 시간에 i번째 항목에 접근할 수 없다. 하지만 스택에서 데이터를 추가하거나 삭제하는 연산은 상수 시간에 가능하다.
스택의 삽입이나 삭제 시 맨 위의 데이터를 삭제하기 때문에 시간복잡도는 늘 O(1)이다. 하지만 특정 데이터를 찾을 때는 데이터를 찾을 때까지 순차적으로 수행해야 하므로 O(n) 시간복잡도를 갖는다.
📌 스택(stack)의 사용 사례
- 재귀 알고리즘
- 재귀적으로 함수를 호출해야 하는 경우에 임시 데이터를 스택에 넣어준다.
- 재귀함수를 빠져 나와 퇴각 검색(backtrack)을 할 때는 스택에 넣어 두었던 임시 데이터를 빼줘야 한다.
- 스택은 이런 일련의 행위를 직관적으로 가능하게 해준다.
- 또한 스택은 재귀 알고리즘을 반복적 형태(iterative)를 통해서 구현할 수 있게 해준다.
- 웹 브라우저 방문기록 (뒤로 가기)
- ex) 가장 마지막에 열린 페이지부터 다시 보여준다.
- 실행 취소(undo)
- ex) 가장 마지막에 실행된 것부터 실행을 취소한다.
- 역순 문자열 만들기
- 가장 마지막에 입력된 문자부터 출력한다.
- 후위 표기법 계산
- 수식의 괄호 검사
- 연산자 우선순위 표현을 위한 괄호 검사
- ex) 올바른 괄호 문자열(VPS: Valid Parenthesis String) 판단하기

