가중치 행렬/변화율/경사하강법/역전파 알고리즘

텐서 플로우 블로그 2.4 신경망의 엔진: 그래디언트 기반 최적화

해당 사이트를 개인 공부 목적으로 재구성한 내용입니다.

가중치 행렬

가중치 행렬(텐서 W)과 편향 b는 층의 속성처럼 볼 수 있다.

• 가중치 = 훈련되는 파라미터 = 훈련 데이터를 신경망에 노출시켜 학습된 정보가 담겨 있다.

가중치 행렬은 초기에 작은 난수로 채워져있다.
피드백 신호에 기초하여 가중치가 점진적으로 조정된다.

이 점진적 조정 = 훈련 = 머신러닝에서의 학습

• 훈련의 과정

1. 훈련 샘플 X, 타깃 y의 배치를 추출
2. X를 사용하여 네트워크 실행(forward pass), 예측 y_pred를 구함
3. y_pred와 y의 차이를 측정 => 해당 배치에 대한 네트워크 손실을 계산
4. 배치에 대한 손실이 조금 감소되도록 네트워크의 모든 가중치를 업데이트

가중치 업데이트

Q. 가중치 업데이트는 어떤 식으로 해야할까?

한 가지 간단한 방법은 네트워크 가중치 행렬의 원소를 모두 고정하고 관심 있는 하나만 다른 값을 적용해 보는 것입니다. 이 가중치의 초깃값이 0.3이라고 가정합시다. 배치 데이터를 정방향 패스에 통과시킨 후 네트워크의 손실이 0.5가 나왔습니다. 이 가중치 값을 0.35로 변경하고 다시 정방향 패스를 실행했더니 손실이 0.6으로 증가했습니다. 반대로 0.25로 줄이면 손실이 0.4로 감소했습니다. 이 경우에 가중치를 –0.05만큼 업데이트한 것이 손실을 줄이는 데 기여한 것으로 보입니다. 이런 식으로 네트워크의 모든 가중치에 반복합니다.

=> 가중치 행렬의 모든 원소마다 두번의 정방향 패스를 계산해야 하므로 매우 비효율적

A. 신경망에 사용된 모든 연산이 미분 가능differentiable하다는 장점을 사용하여 네트워크 가중치에 대한 손실의 그래디언트gradient 26를 계산하는 것이 훨씬 더 좋은 방법

변화율

변화율 함수: x가 바뀜에 따라 f(x)가 어떻게 바뀔지 설명해준다.

f(x+ epsilon_X) = y+ epsilon_y

해당 함수는 연속적이다. x를 조금 바꾸면 y가 조금 변경된다. 함수가 매끈하다. 미분 가능하다. 변화율을 유도할 수 있다.
epsilon_x가 충분히 작다면 어떤 포인트 p에서 기울기 a의 선형함수로 f를 근사할 수 있다.

f(x + epsilon_X) = y + a* epsilon_X

이때 기울기 a : p에서 f의 변화율

• a가 음수: p에서 양수 x만큼 조금 이동하면 f(x)가 감소한다.
• a가 양수: p에서 음수 x만큼 조금 이동하면 f(x)가 감소한다.
• a의 절댓값 = 변화율의 크기 = f(x)의 증가, 감소가 얼마나 빠르게 일어나는가

우리의 목적은 손실함수 f(x)의 값을 줄이는 것!
f(x)의 값을 감소시키고 싶다면 x를 변화율의 방향과 반대로 조금 이동해야 한다.

그래디언트

= 텐서 연산의 변화율
다차원 데이터인 텐서를 입력으로 받는 함수에 변화율 개념을 적용시킨 것

입력 벡터 x, 행렬 W, 타깃 y와 손실 함수 loss가 있다고 가정합시다. W를 사용하여 타깃의 예측 y_pred를 계산하고 손실, 즉 타깃 예측 y_pred와 타깃 y 사이의 오차를 계산할 수 있습니다.

y_pred = dot(W, x)
loss_value = loss(y_pred, y)

입력 데이터 x와 y가 고정되어 있다면 이 함수는 W를 손실 값에 매핑하는 함수로 볼 수 있습니다.

loss_value = f(W)

의 현재 값을 W0라고 합시다. 포인트 W0에서 f의 변화율은 W와 같은 크기의 텐서인 gradient(f)(W0)28입니다. 이 텐서의 각 원소 gradient(f)(W0)[i, j]는 W0[i, j]를 변경했을 때 loss_value가 바뀌는 방향과 크기를 나타냅니다. 다시 말해 텐서 gradient(f)(W0)가 W0에서 함수 f(W) = loss_value의 그래디언트입니다.

그래디언트도 텐서이기 때문에 행,렬이 존재. 그래디언트 텐서의 [i, j] 칸을 변경했을 때 손실함수의 변화율이 gradient(f)(W0)[i , j] 이다!

확률적 경사 하강법

함수의 최솟값 = 변화율이 0이 되는 지점
최솟값을 찾기 위해 우리가 해야할 일은?
변화율이 0인 지점의 값들을 비교해 어떤 포인트의 함수 값이 가장 작은지 확인하는 것

해당 개념을 신경망에 적용하면...

손실함수의 값을 가장 작게 만드는 가중치의 조합을 찾아야 한다
즉 gradient(f)(W) = 0 을 풀어야 한다.

이때 이 식은 네트워크 가중치 개수인 N개의 변수로 이루어져 있다.
= 우리가 여태 풀었던 방정식 풀 듯 풀 수는 없음!

따라서 랜덤한 배치 데이터를 설정한 다음, 현재 손실 값을 토대로 조금씩 파라미터를 수정하는 방식을 활용해야 한다.

더 구체적으로는, 그래디언트를 계산하여 그래디언트의 반대 방향으로 가중치를 업데이트 하면 손실이 매번 조금씩 감소할 것이다. ( = 손실함수의 값이 작아질 것)

미니 배치 확률적 경사 하강법(mini-batch SGD)

1. 훈련 샘플 배치 x와 이에 상응하는 타깃 y를 추출합니다.
2. x로 네트워크를 실행하고 예측 y_pred를 구합니다.
3. 이 배치에서 y_pred와 y 사이의 오차를 측정하여 네트워크의 손실을 계산합니다.
4. 네트워크의 파라미터에 대한 손실 함수의 그래디언트를 계산합니다(역방향 패스(backward pass)).
5. 그래디언트의 반대 방향으로 파라미터를 조금 이동시킵니다. 예를 들어 W -= step * gradient처럼 하면 배치에 대한 손실이 조금 감소할 것입니다.

• step 값을 적절히 고르는 것이 중요하다.
  • 너무 작다 = 곡선을 따라 내려가는데 너무 많은 반복이 필요
  • 너무 크다: 손실 함수 곡선에서 완전히 임의의 위치로 이동시킬 수 있다
• SGD의 종류
  • 진정한(true) SGD: 반복마다 하나이 샘플과 하나의 타깃을 뽑는 방식
  • 배치 SGD: 모든 가용 데이터를 사용하여 반복을 실행. 정확도 높지만 비용 증가.
  • 절충안은 적절한 크기의 미니 배치를 사용하는 것.
• 지역 최솟값 문제

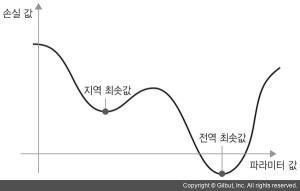
네트워크 파라미터 하나에 대한 손실 값의 곡선

대상 파라미터가 작은 학습률을 가진 SGD로 최적화되었다면 최적화 과정이 전역 최솟값으로 향하지 못하고 지역 최솟값에 갇혀버리는 문제가 발생할 수 있다.

• 모멘텀

마치 손실 곡선 위로 작은 공을 굴리는 것과 같다.

모멘텀은 현재 기울기 값(현재 가속도) 뿐 아니라 (과거의 가속도로 인한) 현재 속도를 함께 고려하여 각 단계에서 공을 움직인다.

= 현재 그래디언트 값 뿐만 아니라 이전에 업데이트한 파라미터에 기초하여 파라미터 w를 업데이트

past_velocity = 0.
momentum = 0.1     # 모멘텀 상수
while loss > 0.01: # 최적화 반복 루프
    w, loss, gradient = get_current_parameters()
    velocity = momentum * past_velocity - learning_rate * gradient
    #velocity를 구할 때 past_velocity가 사용되는 것을 볼 수 있다.
    w = w + momentum * velocity - learning_rate * gradient
    past_velocity = velocity
    update_parameter(w)

역전파 알고리즘

연쇄 법칙(Chain Rule)을 신경망의 그래디언트 계산에 적용한 것

연쇄법칙: f (g(x))' = f '(g(x)) * g'(x)

최종 손실 값에서부터 시작한다.
손실 값에 각 파라미터가 기여한 정도를 계산하기 위해 연쇄 법칙을 적용하여 최상위 층에서 하위 층까지 거꾸로 진행된다.