Day 10 인공지능(2)
탐색
GBFS의 단점은 GBFS가 최정의 경로를 보장해주지 않는 데 있다. 하지만 GBFS를 조금만 수정하면 탐색으로 변경하는 것이 가능하다. 는 시작 노드에서 임의의 노드로의 실제 비용을 뜻하는 경로 비용(path-cost)을 추가했다. 표기법 는 노드 의 경로 비용을 나타낸다. s는 현재 노드를 선택할때 노드의 경로 비용 와 휴리스틱 의 총합인 가 가장 낮은 노드를 선택한다.
가 최적의 경로를 찾기 위해서는 몇 가지 조건을 충족해야 한다. 우선 시작점과 목표점 사이에는 당연히 경로가 존재해야한다. 또한 휴리스틱은 허용 가능해야한다(즉 실제 비용을 초과해서는 안된다). 마지막으로 모든 엣지의 가중치는 0과 같거나 커야한다. 를 구현하려면 GBFS에서 했던 것처럼 먼저 AStarScratch를 정의한다. AstarScrath 구초제에는 값을 저장하기 위해 mActualFromStart라는 float 타입 멤버 변수가 있다는 점이 GBFS에서 사용한 구조체와의 유일한 차이점이다. GBFS 코드와 코드 사이에도 추가적으로 차이점이 존재한다. 노드를 열린 집한에 추가할 때는 의 경로 비용 도 계산해야한다. 그리고 최소 비용의 노드를 선택할 때도 는 비용이 가장 낮은 노드를 선택한다. 마지막으로 는 노드 채택(node adoption)이라는 프로세스를 사용해서 어느 노드가 부모가 되는지를 선택한다. GBFS 알고리즘에서 인접 노드는 항상 현재 노드를 부모 노드로 설정했지만 는 그렇지 않다. 노드 의 경로 비용 값은 해당 노드 부모의 경로 비용 값에 부모로 부터 노드 로의 엣지를 이동하는 데 드는 비용을 더한 값이기 때문이다. 따라서 노드 에 부모를 할당하기 전에 는 값이 더 개선될 수 있을지를 확인해야한다.

위 그림에서 왼쪽에 있는 맵을 보면 GBFS처럼 C2까지 가고 현재 노드는 C3가 되었다. 현재 노드는 자신의 인접 노드를 확인한다. C3의 왼쪽 노드 B3는 = 2이며 부모 노드는 B2이다. 만약 B3가 부모 노드가 C3가 된다면 = 4가 돼 경로 비용 값이 커지게 된다. 그래서 는 이 경우 B3의 부모를 변경하지 않을 것이다. 오른쪽에 있는 맵은 에 의해 계산된 최종 경로를 보여주며, 이 최종 경로는 GBFS를 사용했을 때보다 훨씬 낫다. 노드 채택을 제외하면 코드는 GBFS 코드와 매우 유사하다.
탐색에서 인접 노드에 대한 루프
for (const WeightedEdge* edge : current->mEdges) {
const WeightedEdgeGraphNode* neighbor = edge->mTo;
// 이 노드의 추가 데이터를 얻는다
AStarScratch& data = outMap[neighbor];
// 닫힌 집합에 없는지를 확인
if (!data.mInClosedSet) {
if (!data.mInOpenSet) {
// 열린 집합에 없다면 부모는 반드시 열린 집합에 있어야 한다
data.mParentEdge = edge;
data.mHeuristic = ComputerHeuristic(neighbor, goal);
// 실제 비용은 부모의 실제 비용 + 부모에서 자신으로 이동하는 엣지의 가중치다
data.mActualFromStart = outMap[current].mActualFromStart + edge->mWeight;
data.mInOpenSet = true;
openSet.emplace_back(neighbor);
}
else {
// 현재 노드가 부모 노드가 될지를 판단하고자 새로운 실제 비용을 계산한다
float newG = outMap[current].mActualFromStart + edge->mWeight;
if (newG < data.mActualFromStart) {
// 현재 노드가 이 노드의 부모 노드로 채택됨
data.mParentEdge = edge;
data.mActualFromStart = newG;
}
}
}
}다익스트라 알고리즘
미로 예제로 돌아와서 이제는 미로상에 여러 개의 치즈가 있다고 가정하자. 그리고 쥐를 가장 가까운 치즈를 향해 이동시킨다고 가정하자. 휴리스틱은 어느 치즈가 가장 가까운지를 추정할 수 있고, 알고리즘은 그 치즈에 대한 경로를 찾을 수 있다. 하지만 휴리스틱을 기반으로 선택된 치즈는 실제로 가까운 치즈가 아닐 수 있다. 왜냐하면 휴리스틱은 단지 추정에 불과할 뿐이기 때문이다. 다익스트라 알고리즘(Dijkstra's algorithm)에는 시작 노드는 있지만 목표는 없다. 대신 다익스트라는 그래프 상의 시작 노드에서 모든 도달 가능한 노드까지의 계산한다. 미로 예제에서 다익스트라는 쥐로부터 도달 가능한 모든 노드의 거리를 구한 후 모든 치즈에 대한 실제 이동 비용을 구해서 쥐가 가장 가까운 치즈로 이동할 수 있게 해준다. 코드는 다익스트라 알고리즈으로 변환 가능하다. 먼저 휴리스틱 요소를 제거한다. 그렇다면 = 0인 휴리스틱 함수와 같다는 것을 뜻하며, 실제 비용보다 같거나 낮음을 보장하기 때문에 허용될 수 있다. 다음으로 목표 노드를 재고하고 열린 집합이 빌 때만 루프를 종료하도록 한다. 그러면 코드는 시작점에부터 모든 도달 가능한 노드에 대한 경로 비용 를 계산한다. 이러한 접근은 원래 다익스트라 알고리즘과 조금 다르지만 기능적으로는 동일하다. 일반적이로 게임에서는 같은 경험에 기반을 둔 접근법을 선호한다. 왜냐하면 휴리스틱 기반 접근법이 다익스트라 알고리즘보다 노드 탐색 수가 훨씬 적기 때문이다.
길 따라가기
길 찾기 알고리즘이 경로를 생성하면 AI는 그 경로를 따라가야한다. 경로는 일련의 점으로 추상화할 수 있다. 그러면 AI는 이 경로를 따라 점에서 점으로 이동만 하면 된다. NavComponent라는 MoveComponent의 하위 클래스를 만들어서 경로 이동을 구현한다. MoveComponent는 이미 액터를 앞방향으로 이동시킬 수 있으므로 NavComponent는 액터가 경로를 따라 이동할 때 옳은 방향을 향할 수 있도록 액터를 회전시켜주기만 하면 된다. 먼저 NavComponent에서 TurnTo 함수는 특정 점을 향하고자 액터를 회전시킨다.
void NavComponent::TurnTo(const Vector2& pos) {
// 향하려는 점으로의 벡터를 구한다
Vector2 dir = pos - mOwner->GetPosition();
// 새 각도는 이 방향 벡터의 atan2다
// y값을 반전시킨다
float angle = Math::Atan2(-dir.y, dir.x);
mOwner->SetRotation
}NavComponent는 mNextPont 변수를 가지고 있는데 이 변수는 경로상에서 이동할 다음 지점을 가리킨다. Update 함수는 액터가 mNextPoint에 도달했는지 여부를 테스트한다.
void NavComponent::Update(float deltaTime) {
// 다음 지점에 도착한다면 이동할 새 지점을 얻고 해당 지점을 향해 회전한다
Vector2 diff = mOwner->GetPosition() - mNextPoint;
if (diff.Length() <= 2.0f) {
mNextPoint = GetNextPoint();
TurnTo(mNextPoint);
}
// 액터를 전진시킨다
MoveComponent::Update(deltaTime);
} 위의 코드에서 GetNextPoint 함수는 경로상의 다음 지점을 반환한다는 것을 가정한다. 액터가 경로상의 첫번째 지점에서 시작한다고 가정한다면 mNextPoint는 두 번째 지점 값으로 초기화 되며, 액터는 두 번째 지점을 향하도록 회전한다. 이후 루프에서는 두 번째 지점에 도달할 때까지 선형속도로 액터를 이동시킨다. 이 방식으로 경로를 따라 이동을 갱신하는 데는 한 가지 이슈가 있다. 이 방식은 액터가 너무 빨리 움직여서 한 번에 노드를 뛰어넘지는 않는다고 가정한다. 만약 한 번에 노드를 뛰어넘어버리면 액터와 점은 결코 가까워질 수 없게 된다.
기타 그래프 표현
실시간 액션 게임에서 중립 캐릭터(Non-Player Character, NPC)는 대개 격자상의 사각형에서 사각형으로 이동하지 않는다. 이 때문에 그래프로 세계를 표현하는 것이 더 복잡해지게 된다. 그래서 그 대안으로 경로 노드와 네비게이션 메시를 사용한 2가지 접근법에 대해서 알아본다.
경로 노드(path node, 웨이 포인트 그래프라고도 한다)에서 디자이너는 게임 세계에서 AI가 이동할 수 있는 위치에 경로 노드를 배치한다. 이 경로 노드는 그래프상의 노드로 직접 변환된다. 일반적으로 경로 노드 사이의 엣지는 자동적으로 생성된다. 알고리즘은 다음과 같이 동작한다.
- 각 경로 노드에 대해 해당 노드와 해당 노드 근처에 있는 노드 사이에 장애물이 있는지 여부를 시험한다.
- 각 노드 사이에 차단이 없다면 엣지를 생성한다.
선분 캐스트(line segment cast)나 유사 충돌 테스트가 노드 사이에 차단이 있는지를 결정할 수 있다. 경로 노드를 사용할 시 주된 결점은 AI가 노드 또는 엣지의 위치로만 이동할 수 있다는 것이다. 이 때문에 경로 노드가 삼각형을 형성한다 하더라도 삼각형 내부가 유효한 위치라고 보장할 방법이 없다. 길 찾기 알고리즘은 노드나 엣지가 아닌 위치의 경우 장애물이 존재할 가능성이 있으므로 유효하지 않다고 가정해야 한다. 위의 상황을 피하려면 게임 세계는 AI가 이동에 제약을 받지 않는 공간을 많이 주거나 AI의 이동을 위해 많은 경로 노드를 제공해야 한다. 첫 번째는 AI가 믿음직스럽지 못한 행동을 할 수 있기 때문에 바람직하지 않다. 그리고 두 번째는 단순히 비효율적이다. 노드와 엣지가 많아지면 많아질수록 길 찾기 알고리즘이 해답을 찾는 데는 더욱더 시간이 걸리기 때문이다. 이 상황은 성능과 정확도 간 트레이드 오프가 필요함을 의미한다. 다른 게임에서는 내비게이션 메시(navigation mesh)를 사용한다. 이 접근법에서 그래프상의 각 노드는 볼록 다각형(convex polygon)에 해당하며 인접 노드는 인접한 볼록 다각형이다. 각 노드를 볼록 다각형으로 정의하면 몇 개의 볼록 다각형만으로도 게임 세계의 전체 지역을 나타낼 수 있다. 내비게이션 메시를 사용하면 AI는 볼록 다각형 내부의 어떠한 지점도 안전하게 이동할 수 있다. 즉 AI의 기동성이 향상됐음을 의미한다.

위 그림은 경로 노드와 내비게이션 메시 간 표현 방식의 비교를 보여준다. 내비게이션 메시는 크기가 다른 여러 캐릭터의 이동에 대해 더욱더 효과적이다. 게임에 농장 주위를 돌아다니는 소와 닭이 있다고 가정하자. 닭이 소보다 작다는 걸 감안하면 소는 갈 수 없지만 닭은 접근할 수 있는 지역이 존재할 것이다. 따라서 닭을 위해 설계된 경로 노드 네트워크는 소에 대해서는 제대로 동작하지 않아야한다. 이는 게임이 경로 노드를 사용한다면 각각의 생명체에 대한 별도의 2개 그래프를 가져야한다는 것을 뜻한다. 그에 반해 내비게이션 메시에서 각각의 노드는 볼록 다각형이다. 그래서 내비게이션 메시는 캐릭터가 특정 지역에 적합한지 여부를 계산하는 것이 가능하다. 따라서 게임은 닭과 소 모두에 하나의 내비게이션 메시만을 사용할 수 있다. 내비게이션 메시를 사용하는 대부분의 게임에서는 자동적으로 내비게이션 메시를 생성한다. 내비게이션 메시의 자동 생성은 디자이너가 AI 경로 지정에 따른 영향을 걱정할 필요없이 레벨을 변경할 수 있기에 유용하다. 하지만 내비게이션 메시 생성 알고리즘을 복잡하다. 다행히 내비게이션 메시 생성을 구현한 오프 소스 라이브러리가 있다. 가장 인기 있는 라이브러리 Recast는 3D 레벨의 삼각형 기하로 구성된 내비게이션 메시를 생성한다.
게임 트리
틱택토나 체스 같은 게임은 대부분의 실시간 게임과는 매우 다르다. 이러한 유형의 게임은 플레이어가 2명이며 각 플레이어는 차례를 번갈아가면서 진행한다. 또한 적대적인 상황에 놓여있으므로 두 플레이어가 서로 대결하는 구조다. 이런 유형의 게임에 대한 AI 요구 사항은 실시간 게임의 요구 사항과는 매우 다르다. 게임은 게임의 상태를 유지하는 것이 필요하며, 이 상태는 AI의 의사결정에 영향을 미친다. 게임 상태를 유지하는 한 가지 접근법은 게임 트리(game tree)라는 트리 구조를 사용하는 것이다. 게임 트리에서 루트 노드는 게임의 현재 상태를 나타낸다. 각각의 엣지는 게임에서 가능한 이동을 나타내며 각 이동은 새로운 게임 상태와 연결된다.
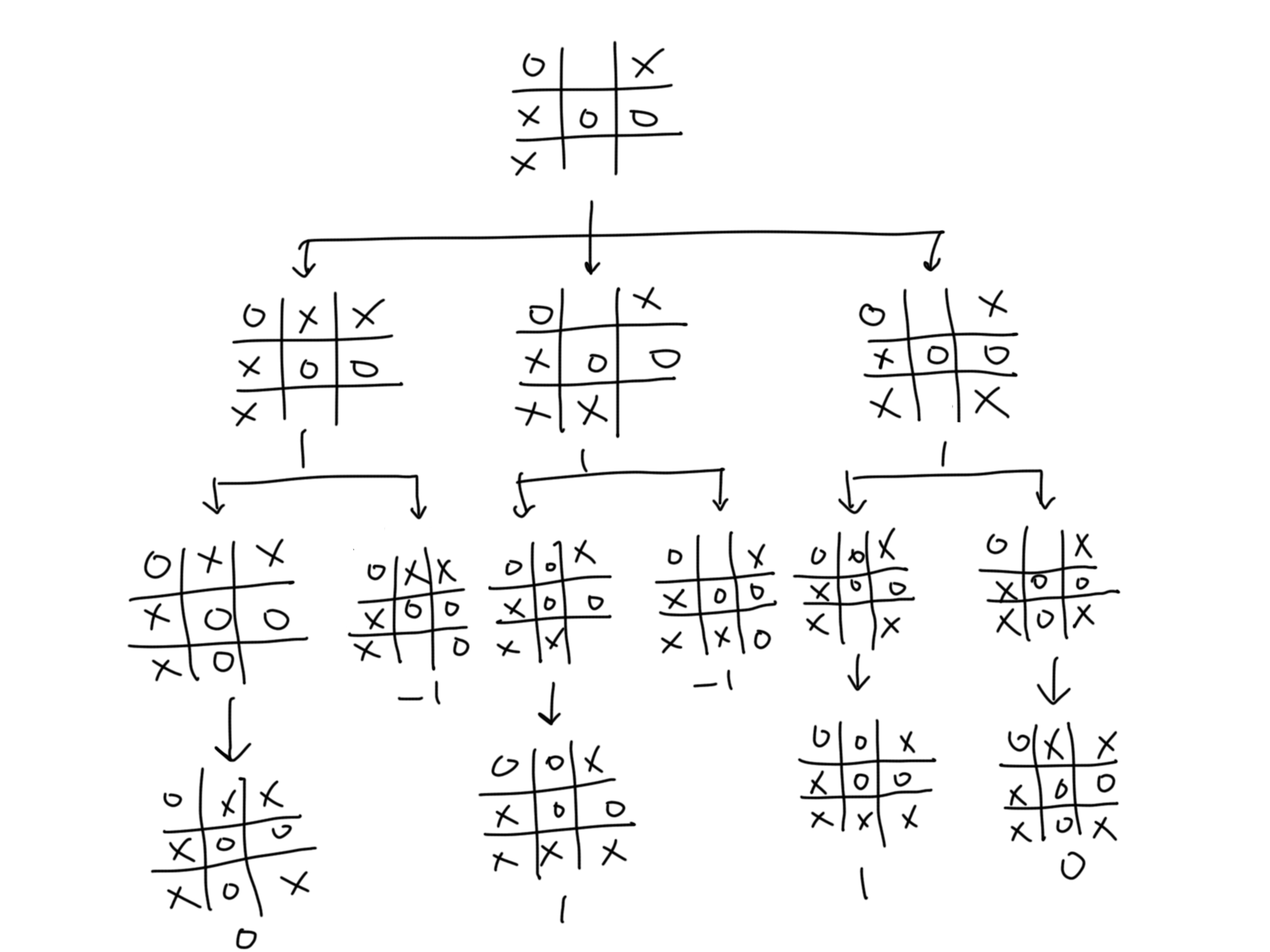
위 그림은 틱택토 게임의 게임 트리이다. 루트 노드로부터 시작해서 현재 플레이어(max player라고도 부른다)는 3가지 이동의 선택이 가능하다. 맥스 플레이어가 이동을 하면 게임 상태는 트리의 첫 번째 레벨이 있는 노드로 전이한다. 그러면 적(min player라고 부른다)는 트리의 두 번째 레벨로 이끄는 이동을 선택ㄷ한다. 이 과정은 게임의 종료 상태를 나타내는 리프 노드(leaf node)에 도달할 때 까지 반복된다. 틱택토 게임에서는 오직 승리, 패배, 무승부 3가지 결과만이 존재한다. 위 게임 트리에서 리프 노드에 할당된 숫자 값은 이런 결과를 나타낸다. 이 값들은 맥스 플레이어의 관점에서 얻은 값이다. 1은 맥스플레이어(X)가 승리했음을 뜻하고, -1은 민플레이어(O)가 승리했음을 뜻한다. 그리고 0은 무승부를 뜻한다. 여러 게임들은 다양한 상태를 가질 수 있따. 틱택토 게임의 경우 상태는 단순한 2D 배열 형식의 보드로 표현하면된다.
struct GameState {
enum SquareState { Empty, X, O };
SquareState mBoard[3][3];
};게임 트리 노드는 해당 노드의 게임 상태뿐만 아니라 자식 노드 리스트도 저장한다.
struct GTNode {
// 자식노드
std::vector<GTNode*> mChildren;
// 이 노드의 게임 상태
GameState mState;
};완전한 게임 트리를 생성하려면 루트 노드를 현재 게임의 상태로 설정하고 이동 가능한 자식 노드를 생성해야한다. 그런 다음 첫 번째 레벨의 각 노드에 대해서도 이 과정을 반복하고 모든 이동이 완료될 때까지 진행한다. 게임 트리의 크기는 잠재적인 이동의 수에 따라 지수적으로 커진다. 틱택토 게임의 경우 게임 트리의 상한성은 9!, 즉 362,880개의 노드가 필요하다. 9! 크기의 노드라면 틱택토 게임은 완전한 게임 트리를 생성해서 평가하는 것이 문제가 되지 않는다. 하지만 체스의 경우 완전한 게임 트리는 의 노드를 가지므로 시간과 공간의 복잡도를 완전히 평가하는 것이 불가능하다. 하지만 불완전한 트리를 다루는 방법도 있다.
미니맥스
미니맥스(minimax) 알고리즘은 2인용 게임 트리를 평가해서 현재 플레이어에 대한 최선의 이동을 결정한다. 미니맥스는 각 플레이어가 자신에게 가장 쵯건인 선택을 한다고 가정한다. 점수는 맥스플레이어의 관점이므로 맥스플레이어는 자신의 점스를 극대화하려는 반면 민플레이어는 맥스플레이어의 점수를 최소화하는 데 집중한다. 미니맥스의 구현을 위해 민플레이어와 맥스플레이어의 행동에 대해 별도의 함수를 사용한다. 두 함수 모두 최초에는 노드가 리프 노드인지를 시험한다. 리프 노드일 경우 GetScore 함수를 호출해서 점수를 계산한다. 다음으로 두 함수는 재귀 호출을 사용해서 최선의 하위 트리를 결정한다. 맥스플레이어의 경우 최선의 하위 트리는 최고의 값을 산출하는 트리다. 반대로 민플레이어의 경우 가장 낮은 값을 가진 하위 트리를 찾는다.
MaxpPlayer와 MinPlayer 함수
float MaxPlayer(const GTNode* node) {
// 리프 노드라면 점수를 리턴한다
if (node->mChildren.empty) {
return GetScore(node->mState);
}
// 최댓값을 가지는 하위 트리를 찾는다
float maxValuew = -std::numeric_limits<float>::infinity();
for (const GTNode* child : node->mChildren) {
maxValue = std::max(maxValue, MinPlayer(child));
}
return maxValue;
}
float MinPlayer(const GTNode* node) {
// 리프 노드라면 점수를 반환한다
if (node->mChildren.empty()) {
return GetScore(node->mState);
}
// 최솟값을 가진 하위 트리를 찾는다
float minValue = std::numeric_limits<float>::infinity();
for (const GTNode child : node->mChildren) {
minValue = std::min(minValue, MaxValue(child));
}
return minValue;
}루트 노드에서 MaxPlayer를 호출하면 맥스플레이어에 대한 최선의 함수를 반환한다. 그러나 이 함수는 AI 플레이어가 알고 싶어하는 최적화된 다음 이동을 지정하지 않는다. 따라서 최선의 이동을 결정하는 코드를 작성해야한다. MinimaxDecide 함수는 MaxPlayer 함수와 비슷하지만 MinimaxDecide 함수는 어떤 자식 노드가 최선의 값을 산출하는지를 추적한다.
const GTNode* MinimaxDecide(const GTNode* root) {
// 최댓값을 가진 하위 트리를 찾고 해당 선택을 저장한다
const GTNode* choice = nullptr;
float maxValue = -std::numeric_limit<float>::infinity()'
for (const GTNode* child : root->mChildren) {
float v = MinPlayer(child);
if (v > maxValue) {
maxValue = v;
choice = child;
}
}
return choice;
}불완전 게임 트리 다루기
완전한 게임 트리를 생성하는 것은 항상 가능하지는 않지만, 미니맥스 코드를 수정하면 불완전 게임 트리에 대응하는 것이 가능하다. 먼저 함수는 노드가 아닌 함수 상태에 따라 동작해야 한다. 다음으로 코드는 자식 노드를 반복하기보다는 주어진 상태로부터 가능한 다음 이동을 반복해야한다. 이렇게 수정하는 것은 미니맥스 알고리즘이 사전에 트리를 생성하기보다는 실행 시간 동안에 트리를 생성한다는 것을 뜻한다. 체스처럼 트리가 너무 크다면 전체 트리를 생성하는 것은 가능하지 않다. 숙련된 체스플레이어가 오직 8번의 다음 수를 예측할 수 있는 것 처럼 AI도 게임 트리의 깊이를 제한해야한다. 즉 코드는 노드가 게임 상태의 마지막에 있지 않다하더라도 리프 노드로써 노드를 다룬다는 것을 뜻한다. 정보에 입각한 결정을 내리기 위해 미니맥스는 이 종료되지 않은 상태가 얼마나 좋은지를 알아야한다. 하지만 종료 상태와는 다르게 정확한 점수를 알아내는 것은 불가능하다. 그러므로 점수를 얻어내는 함수는 종료되지 않은 상태의 품질을 근사화하는 휴리스틱 요소가 필요하다. 즉 점수는 특정 범위 내의 값을 가진다는 것을 의미한다. 휴리스틱 요소를 추가하면 미니맥스가 최선의 결정을 내리는 것을 보장할 수 없다는 걸 의미하기에 주의해야한다. 휴리스틱은 게임 상태의 품질을 근사화하려고 하지만 이 근삿값이 얼마나 정확한지 알 수 없다. 불완전 게임 트리를 사용하면 미니맥스에 의해 선택된 이동은 차선책에 불과하므로 결국 완전 트리의 최선의 선택과 비교해 볼 때 손실이 발생할 수 밖에 없다.
float MaxPlayerLimit(const GameState* state, int depth) {
// depth가 0이거나 상태가 terminal이면 최대 깊이에 도달했다는 것을 뜻한다
if (depth == 0 || state->IsTerminal()) {
return state->GetScore();
}
// 최댓값을 가진 하위 트리를 찾는다
float maxValue = -std::numeric_limits<float>::infinity();
for (const GameState* child : state->GetPossibleMoves()) {
maxValue - std::max(maxValue, MinPlayer(child, depth - 1));
}
return maxValue;
}휴리스틱 함수는 게임에 따라 다양하다. 예를 들어 단순한 체스 게임의 휴리스틱 함수는 각 플레이어가 가진 말의 수를 세고, 각각의 말에 가중치를 부여할 수 있다. 하지만 이런 단순한 휴리스틱의 결점은 때때로 짧은 기간에 장기말을 희생하는 것이 긴 기간동안 장기말을 살려놓는 것보다 좋을 때도 있다. 다른 휴리스틱은 왕의 안전이나 여왕의 기동력, 체스판 중앙의 통제 등을 고려한다. 다른 몇 가지 요인들이 휴리스틱에 영향을 많이 미친다. 보다 복잡한 휴리스틱을 위해서는 많은 연산이 필요하다. 하지만 대부분의 게임에서는 AI의 연산에 시간 제한이라는 제약을 설정한다. 예를 들어 체스 게임 AI는 10초 이내로 다음 턴을 결정해야할 수도 있다. 이런 시간 제한 설정은 AI의 지능을 낮출 수 있으므로 탐색하려는 깊이 및 휴리스틱 복잡성 등과 균형을 맞춰야 한다.
알파 베타 가지치기
알파 베타 가지치기(Alpha-beta pruning)는 평가하려는 노드의 수를 줄이는 미니맥스 알고리즘의 최적화 기법이다. 그래서 알파 베타 가지치기는 계산 시간을 증가시키지 않고 탐색하려는 최대 깊이를 증가시키는 것이 가능하다.

위 그림은 알파 베타 가지치기로 단순화된 게임 트리를 보여준다. 형제 노드에 대한 평가 순서를 왼쪽에서 오른쪽 순으로 한다고 가정했을 때 맥스플레이어는 먼저 하위 트리 B를 조사한다. 그러면 민플레이어는 값이 5인 리프 노드를 보게 된다. 그래서 민플레이어는 5와 다른 값 중에서 하나를 선택하는데 이 다른 값이 5보다 크면 민플레이어는 5를 선택한다. 그래서 이 상황은 하위 트리 B로부터 얻을 수 있는 상한선은 5이며, 하한선은 음의 무한대 값이라는 것을 뜻한다. 민플레이어는 계속해서 값이 0인 리프 노드를 보게 되며, 민플레이어는 최소 점수를 원하므로 값이 0인 리프 노드를 선택한다. 제어는 이제 하위트리 B가 0의 값을 가진다는 것을 아는 맥스플레이어 함수로 돌아온다. 계속해서 맥스플레이어는 하위 트리 C를 조사한다. 민플레이어는 먼저 -3의 값을 가진 리프 노드를 살펴본다. 이전과 마찬가지로 하위트리 C의 상한선은 -3이다. 그러나 맥스플레이어는 이미 하위 트리 B가 0의 값을 가진 알고 있으며 이 값은 맥스플레이어 입장에서 -3보다 좋다. 즉 맥스플레이어는 하위 트리 C로부터 하위 트리 B보다 더 나은 결과를 얻을 수 없는 것이다. 알파 베타 가지치기는 이를 인식해서 결과적으로 C의 다른 자식 노드를 조사하지 않는다. 알파 베타 가지치기는 알파와 베타라는 2개의 변수를 필요로 한다. 알파는 현재 레벨이나 그 이상에서 맥스 플레이어에게 보장하는 최고 점수다. 반대로 베타는 현재 레벨이나 그 이상에서 민플레이어에게 보장하는 최고 점수이다. 다시 말해서 알파와 베타는 점수의 상한과 하한의 경계값이다. 처음의 알파는 음의 무한대 값이고 베타는 양의 무한대 값이다. 즉 두 플레이어는 최악의 점수로 시작한다.
AlphaBetaDecide 구현
const GameState* AlphaBetaDecide(const GameStae* root, int maxDepth) {
const GameState* choice = nullptr;
// 알파는 음의 무한대, 베타는 양의 무한대 값으로 시작한다
float maxValue = -std::numeric_limits<float>::infinity();
float beta = std::numeric_limits<float>::infinity();
for (const GameState* child : root->GetPossibleMoves()) {
float v = AlphaBetaMin(child, maxDepth - 1, MaxValue, beta);
if (v > maxValue) {
maxValue = v;
choice = child;
}
}
return choice;
}AlphaBetaMax 구현
float AlphaBetaMax(const GameState* node, int depth, float alpha, float beta) {
if (depth == 0 || node->IsTerminal()) {
return node->GetScore();
}
float maxValue = -std::numeric_limits<float>::infinity();
for (const GameState* child : node->GetPossibleMoves()) {
maxValue = std::max(maxValue, AlphaBetaMin(child, depth - 1, alpha, beta));
if (maxValue >= beta) {
return maxValue; // 베타 가지치기
}
alpha = std::max(maxValue, alpha); // 알파값 증가
}
return maxValue;
}AlphaBetaMax 함수는 MaxPlayerLimit 함수를 토대로 구현됐다. 어떤 반복에서도 최댓값이 베타값보다 같거나 크다면 이전 베타값은 더 좋아질 수 없다. 이 상황에서는 함수가 남아 있는 형제 노드를 확인할 필요가 없기에 결과를 반환하고 종료한다. 그렇지 않고 최댓값이 베타값보다 작고 알파값보다 크다면 코드는 알파값을 증가시킨다.
AlphaBetaMin 구현
float AlphaBetaMin(const GameState* node, int depth, float alpha, float beta) {
if (depth == 0 || node->IsTerminal()) {
return node->GetScore();
}
float minValue = std::numeric_limits<float>::infinity();
for (const GameState* child : node->GetPossibleMoves()) {
minValue = std::min(minValue, AlphaBetaMax(child, depth - 1, alpha, beta));
if (minValue <= alpha) {
return minValue // 알파 가지치기
}
beta = std::min(minValue, beta); // 베타값을 감소시킨다
}
return minValue;
}마찬가지로 AlphaBetaMin 함수는 최솟값이 알파와 같거나 더 작은지를 검사한다. 이 경우에는 이전 알파값이 더 좋아질 수 없으므로 함수는 종료된다. 그렇지 않으면 코드는 상황에 따라 베타값을 감소시킨다. 자식 노드에 대한 평가 순서는 내쳐지는 노드 수에 영향을 미친다. 이는 일관된 깊이 제한을 가진다고 하더라도, 시작 상태에 따라 실행 시간이 달라질 수 있음을 끗한다. 이런 상황은 AI가 고정된 시간 제한을 가진다면 문제가 된다. 불완전한 탐색은 AI가 어떤 이동을 해야 할지 결정 못했다는 것을 의미하기 때문이다. 이에 대한 해결책으로서, 깊이 제한값을 증가시키면서 알고리즘을 여러 번 실행하는 반복적인 심화 방법이 대안이 될 수 있겠다. 예를 들어 먼저 3의 깊이 제한으로 알파 베타 가지치기를 실행해 기준이 되는 이동을 산출한다. 그리고 시간이 다 소진될때까지 4의 깊이 제한으로 실행하고 계속해서 5의 깊이 제한으로 실행한다. 이전 반복에서 기본 이동을 구했기 때문에 특정 깊이에서 불완전한 탐색을 했다 하더라도 AI가 어떤 이동을 해야할지 선택하는데 문제가 없다.
