Game Programming in C++ - Day 9

Day 9 인공지능(1)

상태 기계 행위(State Machine Behaviors)

아주 간단한 게임에서는 AI는 항상 같은 행위를 한다. 예를 들어 2인용 퐁 게임에서 AI는 공이 움직일 때 공의 위치를 추적한다. 이 행위는 게임이 진행되는 동안 바뀌지 않지만 다른 게임에서는 AI의 행동이 변할 때가 있다. 예를 들어 팩맨에서 유령은 3가지 다른 행동을 한다.

• 플레이어 쫓아가기
• 흩어지기
• 플레이어로부터 멀어지기

이런 행동의 변화를 표현하는 한 가지 방법으로 각 행동이 하나의 상태를 가지는 상태 기계(State Machine)란 것이 있다.

상태 기계 설계하기

상태 그 자체는 부분적으로 하나의 상태 기계만 정의한다. 그래서 상태 기계 설계에 있어서는 상태 기계를 변경하거나 상태 기계 간 전이(transition)하는 방법을 결정하는 것이 중요하다. 또한 각 상태는 해당 상태에 진입하거나 빠져나갈 때 특정 행위를 수행한다. 그래서 게임 캐릭터의 AI에 상태 기계를 구현할 때는 서로 다른 상태가 어떻게 상호 연결되어 있는지 계획해야한다. 스텔스 게임에서의 기본 가드 캐릭터로 예를 들면 기본적으로 가드는 미리 정해진 경로를 순찰한다. 그리고 플레이어를 감지하면 공격하고 어떤 행동을 하고 있던간에 플레이어에게 공격을 받아 체력이 바닥나면 사망한다. 그래서 가드 AI는 3가지의 상태를 갖는다

• 순찰(patrol)
• 공격(attack)
• 사망(death)

다음으로 각 상태에 대한 정의를 정의해야 한다. 사망 상태 전이는 간단하다. 가드가 치명적인 데미지를 받으면 사망으로 전이한다. 사망은 현재의 상태에 관계없이 일어난다. 이것은 기본적인 것이고 일반적인 스텔스 게임의 AI 캐릭터는 더 복잡하다. 예를 들어 가드가 순찰 상태에서 수상한 소리를 들었다면 가드는 플레이어를 찾는 조사(investigate) 상태가 된다. 그리고 플레이어를 찾았을 때 바로 공격할 수도 있지만 경고(alert) 상태에 진입할 수 있다. 경고 상태에서는 확률적으로 플레이어를 공격하거나 알람(alarm) 상태에 들어가 바로 공격하는 대신에 일정시간 대기한 후에 공격할 수 있다. 그렇다면 처음에 설정한 가드의 상태보다 더 복잡한 상태를 구현할 수 있다.

기본 상태 기계 구현

상태 기계를 구현하는 데는 몇 가지 방법이 존재한다. 적어도 코드는 현재 상태를 기반으로 AI의 행위를 갱신해야한다. 그리고 상태 기계는 상태 진입 및 상태 종료 시의 액션을 지원해야 한다. AIComponent 클래스는 이러한 상태 행위를 캡슐화한다. 여러 상태를 표현하기 위해 열거형을 사용하면 좋다.

enum AIState {
	Patrol,
    Death,
    Attack
};

또한 각 상태에 대한 별도의 갱신 함수를 정의해야한다.

• UpdatePatrol
• UpdateDeath
• UpdateAttack

AIComponent::Update 함수는 AIState 멤버 변수에 대한 switch 문을 가지고 있으며, 현재 상태에 해당하는 갱신 함수를 호출한다.

void AIComponent::Update(float deltaTime) {
	swtich (mState)
    {
    case Patrol:
    	UpdatePatrol(deltaTime);
        break;
    case Death:
    	UpdateDeath(deltaTime);
        break;    
	case Attack:
    	UpdateAttack(deltaTime);
        break;
    default:
    	break;
}

별도의 ChangeState 함수로 상태 기계의 전이를 다룰 수 있다. 여러 갱신 함수는 ChangeState 함수를 호출해서 상태 전이를 초기화한다.

void AIComponent::ChangeState(State newState) {
	// 현재 상태 빠져 나가기
    // switch 문을 사용해서 일치하는 Exit 함수 호출
    // ...
    mState = newState;
    // 현재 상태 진입하기
    // switch 문을 사용해서 일치하는 Enter 함수 호출
    // ...
}

이러한 구현은 간단하지만 문제가 있다. 먼저 확장성이 부족하다. 상태를 많이 추가하면 할수록 Update와 ChangeState 둘 다 가독성이 떨어지계 된다. 또한 별도의 Update, Enter, Exit 함수가 많아지면 코드를 다루기가 어렵게 된다. 또한 여러 AI 간에 기능을 혼합하고 일치시키는 것도 쉽지 않다. 여러 AI 캐릭터는 일부 기능을 공유할 수 있는데 예를 들어 두 AI가 대부분의 상태 기계는 다르지만 둘 다 순찰 상태는 가지고 있다고 가정하면 이 둘 AI 컴포넌트 사이에 순찰 코드를 공유하는 것은 쉽지 않다.

클래스로서의 상태

각 상태를 클래스를 사용해서 나타내는 방법이 있다. 먼저 AIState라는 모든 상태에 대한 기본 클래스를 정의한다.

class AIState {
public:
	AIState(class AIComponent* owner)
    	:mOwner(owner)
    { }
    // 각 상태의 구체적인 행동
   	virtual void Update(float deltaTime) = 0;
    virtual void OnEnter() = 0;
    virtual void OnEixt() = 0;
    // 상태의 이름 얻기
    virtual const char* GetName() const = 0;
protect:
	class AIComponent* mOwner;
};

AIState 기본 클래스는 상태를 제어하고자 몇 가지 가상 함수를 포함한다. Update 함수는 상태를 갱신하며, OnEnter 함수는 상태 진입 시의 전이 코드를 구현한다. 그리고 OnExit에서는 종료 전이 코드를 구현한다. GetName 함수는 상태에 대해 사람이 읽을 수 있는 이름 문자열을 반환한다. 또한, AIState 클래스는 mOwner 멤버 변수를 사용해서 AIComponent와 연관시켜야 한다. 그리고 AIComponent 클래스를 선언한다.

class AIComponent : public Component {
public:
    AIComponent(class Actor* owner);
    
    void Update(float deltaTime) override;
    void ChangeState(const std::string& name);
    
    // 새 상태를 맵에 추가한다.
    void RegisterState(class AIState* state);
private:
	// 상태의 이름과 AIState 인스턴스를 매핑한다
    std::unordered_map<std::string, class AIState*> mStateMap;
    //AI의 현재 상태
    class AIState* mCurrentState;
};

AIComponent는 상태 이름과 AIState 인스턴스 포인터의 해시 맵을 가진다. RegisterState 함수는 AIState 함수를 인자로 받아서 맵에 해당 상태를 추가한다.

void AIComponent::RegisterState(AIState* state) {
	mStateMap.emplace(state->GetName(), State);
}

AIComponent::Update 함수 또한 간단하다. 이 함수는 단순히 상태가 존재하면 해당 상태의 Update 함수를 호출한다.

void AIComponent::Update(float deltaTime) {
	if (mCurrentState) {
    	mCurrentState->Update(deltaTime);
    }
}

하지만 ChangeState 함수는 몇 가지 작업을 수행한다. 먼저 ChangeState 함수는 현재 상태의 OnExit 함수를 호출한다. 다음으로 이 함수는 맵에서 변경하고자 한느 상태를 찾으려고 시도한다. 이 상태를 찾으면 ChangeState 함수는 mCurrentState를 새로운 상태로 변경한 뒤 이 새로운 상태의 OnEnter 함수를 호출한다. 맵에서 다음 상태를 찾을 수 없으면 에러 메세지를 출력하고 mCurrentState를 nullptr 로 설정한다.

void AIComponent::ChangeState(const std::string& name) {
	// 먼저 현재 상태를 빠져 나온다
    if (mCurrentState) {
    	mCurrentState->OnExit();
    }
    
    // 맵에서 새로운 상태를 찾는다
    auto iter = mStateMap.find(name);
    if (iter != mStateMap.end()) {
    	mCurrentState = iter->second;
        // 새로운 상태로 진입한다
        mCurrentState->OnEnter();
    }
    else {
   		SDL_Log("Could not find AIState %s in state map", name.c_str());
        mCurrentState = nullptr;
    }
}	

AIPatrol라는 AIState의 서브클래스를 선언하면 다음과 같다.

class AIPatrol : public AIState {
public:
	AIPatrol(class AIComponent* owner);
    
    // 이 상태에 대한 행위를 재정의
    void Update(float deltaTime) override;
    void OnEnter() override;
    void OnExit() override;
    
    const char* GetName() const override
    { return "Patrol"; }
};

그런 다음 Update, OnEnter, OnExit의 구체적인 행위를 구현한다. AIPatrol에서는 캐릭터가 죽을 때 AIDeath로 상태를 변경한다. 전이를 초기화하기 위해 소유자 컴포넌트의 ChangeState 함수를 호출한다. ChangeState 함수에는 새로운 상태의 이름을 인자로 넘긴다.

void AIPatrol::Update(float deltaTime) {
	// 일부 갱신 작업
    // ...
    bool dead = /* 자신이 죽었는지 판단 */;
    if (dead) {
    	// AI 컴포넌트에 상태를 변경하라고 알림
        mOwner->ChangeState("Death");
    }
}   

ChangeState 호출에서 AIComponent는 자신의 상태 맵을 살펴보고 Death라는 이름의 상태를 찾으면 이 상태로 전이한다. 상태들을 AIComponent의 상태 맵에 등록하려면 먼저 Actor와 Actor의 AIComponent를 생성한다. 그런 다음 RegisterState 함수를 호출해서 추가하려는 상태를 상태 기계에 등록한다.

Actor* a = new Actor(this);
// AIComponent 생성
AIComponent* aic = new AIComponent(a);
// AIComponet에 상태 등록
aic->RegisterState(new AIPatrol(aic));
aic->RegisterState(new AIDeath(aic));
aic->RegisterState(new AIAttack(aic));

그런 다음 AIComponent를 순찰 상태로 설정하려면 다음과 같이 ChangeState를 호출한다.

aic->ChangeState("Patrol");

이러한 접근법은 각 상태가 별도의 서브클래스에서 구현됐으므로 유용하다. 이를 통해 AIComponent는 간결함을 유지할 수 있기 때문이다. 또한 여러 다양한 AI 캐릭터가 같은 상태를 재사용하기 쉽게 해준다. 새 액터의 AIComponent에다가 원하는 상태를 등록만 해주면 되기 때문이다.

길 찾기

길 찾기(path finding) 알고리즘은 두 지점의 경로상에 있는 장애물을 피해서 길을 찾는다. 이 길 찾기의 복잡성은 두 점 사이에는 여러 다양한 결로 집합이 존재할 수 있다는 사실에 있다. 하지만 이러한 경로 중 아주 적은 수의 경로만이 최단 경로이다. 아래 그림은 A와 B 사이의 잠재적 경로를 보여준다.
빨간 경로로 이동하는 AI는 지능적으로 보이지 않는다. 왜냐하면 파란 경로가 더 최단 경로이기 때문이다. 따라서 최단 경로를 찾기 위해서 모든 가능한 경로를 효율적으로 탐색하기 위한 방법이 필요하다.

그래프

길 찾기 문제를 풀기 전에 먼저 AI가 통과할 수 있는 게임 세계의 부분을 표현하는 방법이 필요하다. 일반적으로는 그래프(graph) 데이터 구조를 많이 선택한다. 그래프는 일련의 노드(node)를 포함한다. 이 노드들은 엣지(edge)를 통해 서로 연결된다. 이 엣지는 방향성이 없는 경우가 있는데 방향성이 없다는 것은 양방향으로 이동할 수 있다는 걸 의미한다. 반면 방향성이 있다는 것은 엣지가 오직 한 방향으로만 이동할 수 있다는 걸 뜻한다. AI가 플랫폼에서 뛰어내릴 수는 있지만 다시 뛰오 올라갈 수는 없는 경우 방향성이 있는 엣지를 사용하면 된다. 엣지는 선택적으로 엣지와 관련된 가중치(weight)를 가질 수 있는데, 가중치는 엣지를 이동하는 데 드는 비용을 나타낸다. 게임에서 가중치는 노드 사이의 최소한의 거리를 뜻한다. 그러나 이 가중치는 해당 엣지를 이동하는 것이 얼마나 어려운지를 나타내는 것으로 사용할 수 있다. 그래프를 나타내는 데는 여러 가지 방법이 있으나 Game Programming in C++에서는 인접 리스트(adjacency list)를 사용한다. 이 표현에서는 각 노드는 std::vector를 사용해서 인접 노드 컬렉션을 가진다. 그래서 그래프를 그런 노드의 단순한 집합이다.

struct GraphNode {
	// 각 노드는 인접 노드의 포인터들을 가지고 있다
    std::vector<GraphNode*> mAdjacent;
};

struct Graph {
	// 그래프는 노드를 포함한다
    std::vector<GraphNode*> mNode;
};

가중 그래프에서 각 노드는 연결된 노드 리스트 대신에 외부로 향하는 엣지를 저장한다.

struct WeightedEdge {
	// 이 엣지에 어떤 노드가 연결되어 있는지
    struct WeightedGraphNode* mFrom;
    struct WeightedGraphNode* mTo;
    // 이 엣지의 가중치
    float mWeight;
};
struct WeightedGraphNode {
	// 외부로 향하는 엣지를 저장한다
    std::vector<WeightedEdge*> mEdges;
}; 

엣지의 시작과 끝을 참조하면 노드 A에서 B로 향하는 방향성 있는 엣지의 지원이 가능하다. 이 경우에는 노드 B의 mEdges 벡터가 아니라 노드 A의 mEdges 벡터에 엣지를 추가해야 한다. 방향성이 없는 엣지를 원한다면 간단히 각 방향별로 하나씩해서 총 2개의 방향성있는 엣지를 추가하면 된다. 여러 게임은 여러 가지 방식을 사용해서 그래프를 통해 게임 세계를 나타낸다. 세계를 격자 형태의 사각형으로 분할하는 것은 일반적인 접근법이다. 하지만 이러한 방식이 모든 게임에 적용되는 것은 아니다.

너비 우선 탐색(Breadth-First Search)

게임이 사각형 격자로 설계된 미로에서 일어난다고 가정하면 게임은 오직 4개의 기본적인 방향으로의 이동만 가능하다. 미로에서 각각의 이동은 길이가 일정하므로 가중치 없는 그래프로 이 미로를 표현할 수 있다. 이 미로에서 AI 쥐와 목표물인 치즈가 있다고 할때 미로를 표현한 그래프의 시작 노드에서 치즈까지의 최단거리를 구한다고 했을때 한 가지 접근법은 먼저 시작 노드로부터 한 칸 떨어진 모든 노드를 검사한다. 이 과정에서 치즈가 발견되지 않으면 그 다음은 두 칸 떨어진 모든 노드를 검사한다. 이 과정은 치즈가 발견되거나 더이상 유효한 이동이 없을 때까지 반복한다. 이 알고리즘은 가까운 노드에서 목포를 발견할 수 없으면 더 먼 노드를 고려하므로 치즈에 대한 최단 경로를 놓치지 않을 것이다. 이 방식을 너비 우성 탐색(BFS)이라고 한다. BFS 알고리즘은 엣지에 가중치가 없거나 모든 엣지가 양의 같은 가중치를 가질 경우 최단 경로를 찾는 것을 보장한다. BFS 알고리즘을 수행하는 동안 몇 가지 데이터를 기록하면 최소한의 이동 횟수로 경로를 재구성할 수 있다. 경로가 계산되면 AI 캐릭터는 이 경로를 따라 이동할 수 있게 된다. BFS 동안에 각 노드는 직전에 방문한 노드를 알아야한다. 부모노드라 불리는 해당 노드는 BFS가 완료된 후 경로를 재구성하는 데 도움이 된다. 이 데이터를 GraphNode 구조체에 추가할 수 있지만 GraphNode는 부모 노드에 의해 데이터가 변경되지 않도록 분리하는 것이 좋다. 부모 노드는 시작 노드와 목표 노드에 따라 변하기 때문이다. 또한 데이터를 분리하면 멀티 스레드를 통해 동시에 몇 개의 경로를 계산할 경우 각 탐색이 서로 간섭하지 않는 것을 보장할 수 있다. 이를 위해 먼저 NodeToParentMap이라 불리는 맵 타입을 정의한다. 이 맵은 키와 값이 GraphNode 포인터인 unordered map이다.

using NodeToParentMap = std::unordered_map<const GraphNode*, const GraphNode*>;

BFS를 구현하는 가장 간단한 방법은 큐의 사용이다. 먼저 시작 노드를 큐에 추가하고 루프에 진입한다. 각 반복에서는 큐로부터 노드를 꺼낸 뒤 해당 노드의 이웃을 큐에 추가한다. 부모 맵을 확인함으로써 이미 검사한 노드를 큐에 다시 추가하는 걸 피할 수 있다. 큐에서 꺼낸 노드의 이웃 노드는 outMap에 대괄호를 사용해서 자신의 부모가 등록되어 있는지 조회한다. 키 값이 이미 맵에 존재한다면 검사가 된 노드이므로 큐에 추가하지 않는다. 키가 맵상에 존재하지 않으면 outMap은 nullptr을 반환하며, 이는 해당 노드의 부모가 설정되어 있지 않았음을 의미하므로 노드 맵에 부모를 등록하고 자신을 큐에 추가한다. 시작 노드와 목표 노드 사이에 어떤 경로도 존재하지 않는다면 루프는 종료될 것이다. 알고리즘이 시작점에서 도달 가능한 모든 노드를 검사했기 때문이다. 모든 가능성이 소진됐으므로 큐는 비게 되고 루프는 종료된다.

bool BFS(const Graph& graph, const GraphNode* start, 
	const GraphNode* goal, NodeToParentMap& outMap) {
	// 경로를 찾았는지 알 수 있는 플래그
    bool pathFound = false;
    // 고려해야할 노드
    std::queue<const GraphNode*> q;
    
    // 시작 노드를 큐에 넣는다
   	q.emplace(start);
    
    while (!q.empty()) {
    	// 큐에서 노드를 꺼낸다
        const GraphNode* current = q.front();
        q.pop();
        if (current == goal)
        {
        	pathFound = true;
            break;
        }
        
        // 큐에 없는 인접 노드를 꺼낸다
        for (const GraphNode* node : current->mAdjacent) {
        	// 시작 노드를 제외하고
            // 부모가 null 이면 큐에 넣지 않은 노드다
            const GraphNode * parent = outMap[node];
            if (parent == nullptr && node != start) {
            	// 이 노드의 부모 노드를 설정하고 큐에 넣는다
               	outMap[node] = current;
                q.emplace(node);
            }
       	}
    }
    
    return pathFound;
}

Graph g가 존재한다고 가정했을 때 다음 두 라인처럼 코드를 작성하면 그래프의 두 노드 사이에서 BFS를 수행할 수 있다.

NodeToParentMap map;
bool found = BFS(g, g.mNodes[0], g.mNodes[9], map);

BFS가 성공하면 outMap의 부모 포인터를 사용해서 경로 재구축이 가능하다. 목표 노드에서 부모 포인터 체인을 따라가면 시작 노드에 도달하게 되고 목표점에서 시작점까지의 경로를 얻게 된다. 그 반대인 시작점에서 목표점까지 경로를 얻고싶으면 스택을 이용해서 경로를 반전시키거나 탐색 자체를 반전시키는 방법이 있다. 목표 노드부터 시작해서 시작 노드까지 탐색을 하면 되는 것이다. BFS는 경로가 존재한다면 시작 노드와 목표 노드 사이의 경로를 항상 발견한다. 하지만 가중 그래프에서 BFS는 최단 경로의 발견을 보장하지 않는다. 왜냐하면 BFS는 엣지의 가중치를 전혀 고려하지 않기 때문이다. BFS에서 모든 엣지의 이동값을 같다.

위 그림처럼 시작 노드에서 목표 노드까지 직선거리가 최단 거리지만 BFS는 단 두 번의 이동만 필요한 실선 경로를 반환한다. BFS 관련 또 다른 문제점은 노드가 목표 노드의 반대 방향에 있다하더라도 노드를 테스트하는데 있다. 좀 더 복잡한 알고리즘을 적용하면 최적의 솔루션을 찾는 과정에서 테스트할 노드의 수를 줄이는 것은 가능하다. 좀 더 복잡한 알고리즘을 적용하면 최적의 솔루션을 찾는 과정에서 테스트할 노드의 수를 줄이는 것은 가능하다. 게임에서 사용된 대부분의 다른 길 찾기 알고리즘은 전반적으로 BFS와 같은 구조를 갖고 있다. 반복마다 조사할 하나의 노드를 선택하고 해당 노드의 이웃을 데이터 구조에 추가한다. 차이점은 여러 길 찾기 알고리즘이 다양한 순서로 노드를 평가한다는데 있다.

휴리스틱

많은 탐색 알고리즘은 예상되는 결과를 근사하는 함수 휴리스틱(heuristic), 즉 경험적 방법에 의존한다. 길 찾기에서 휴리스틱은 주어진 노드로부터 목표 노드까지의 예상되는 비용이다. 휴리스틱은 경로를 더 빠르게 찾는 데 도움을 줄 수 있다. 예를 들어 BFS의 각 반복마다 BFS는 다음 노드가 목표로 부터 멀어지는 방향에 있다고 하더라도 큐에서 해당 노드를 꺼냈었다. 휴리스틱을 사용하면 특정 노드가 목표에 얼마나 가까운지를 예상할 수 있으며 그래서 우선 좀 더 가까운 노드를 살펴본다. 이렇게 하면 길 찾기 알고리즘은 반복 횟수를 줄여서 빨리 종료하는 것이 가능해진다. 표기법은 h(x)는 휴리스틱을 나타낸다. $x$는 그래프상의 노드다. 그래서 $h(x)$는 노드 $x$에서 목표 노드까지의 추정 비용을 뜻한다. 휴ㅜ리스틱 함수는 노드 $x$에서 목표까지의 실제 비용보다 같거나 작으면 항상 허용된다. 휴리스틱이 이따금 실제 비용보다 크게 평가한다면 이 휴리스틱은 허용돼서는 안된다.

사각형 격자에서 휴리스틱을 계산하는 방법은 두 가지가 있다. 예를 들어 위 그림에서 왼쪽에 있는 맨해튼 거리 휴리스틱은 대도시의 도시 구획을 따라 이동하는 것과 유사하다. 건물은 5블럭 떨어져 있지만 길이가 5블록인 루트는 다양하다. 맨해튼 거리에서는 대각선 이동이 유효하지 않다고 가정한다. 대각선 이동이 유효하면 맨해튼 거리는 종종 비용을 초과평가해서 휴리스틱을 허용 가능하지 않게 한다. 2D 격자에서 맨해튼 거리는 다음과 같은 거리 공식으로 계산한다.

$h(x) = |start.x - end.x| + |start.y - end.y|$

휴리스틱의 두 번째 타입은 오른쪽에 있는 유클리드 거리이다. 이 휴리스틱은 시작과 목표의 일직선 경로를 평가한다. 유클리드 거리는 사각형 격자보다 좀더 복잡한 세계에서 잘 동작한다. 2D에서 유클리드 거리 방정식은 다음과 같다.

$h(x) = \sqrt{(start.x - end.x)^2 + (start.y - end.y)^2}$

유클리드 거리 함수는 맨해튼 거리에서는 허용되지 않는 경우에도 거의 항상 허용 가능하다. 이는 유클리드 거리가 추천할 만한 휴리스틱 함수라는 것을 뜻한다. 그러나 맨해튼 휴리스틱은 제곱근을 사용하지 않으므로 계산에 있어서는 더 효율적이다. 유클리드 거리 휴리스틱이 실제 비용을 초과 평가하는 유일한 경우는 게임이 레벨에 존재하는 두 노드 사이를 텔레포트하는 것과 같이 비유클리드 이동을 허용하는 경우이다. 두 휴리스틱 함수는 시작 노드로부터 목표 노드까지 이동하는 실제 비용을 낮게 평가한다. 왜냐하면 휴리스틱 함수는 인접리스트에 관해 아무런 정보도 없기 때문이다. 그래서 특정 지역을 지날 수 있는지 없는지는 휴리스틱은 알 수 없다. 이 상황은 휴리스틱이 노드 $x$가 목표 노드에 얼마나 가까운지에 대한 하한선이 되므로 괜찮다. 즉 휴리스틱은 노드 $x$가 적어도 휴리스틱이 산출한 거리만큼은 떨어져 있음을 보장한다. 이러한 사실은 상대적인 관점에서 유용한 정보다. 예를 들어 휴리스틱은 노드 A나 B중 어느 노드가 목표 노드에 더 가까운지를 결정할 수 있다.

탐욕 최우선 탐색

BFS는 FIFO 순으로 노드를 다루기 위해 큐를 사용했다. 탐욕 최우선 탐색(GBFS, Greedy Best-First Search)은 대신 어느 노드 다음에 고려해야하는지를 결정하기 위해 휴리스틱 함수를 사용한다. GBFS는 합리적인 길 찾기 알고리즘처럼 보일 수 있지만 최단 경로를 보장해주지 않는다.

위 그림은 GBFS 탐색의 결과를 보여준다. 경로는 곧장 아래로 이동하는 것이 아니라 시작점에서 오른쪽으로 이동해서 4개의 이동이 추가됐다. GBFS는 탐색을 진행하는 동안 하나의 큐를 사용하는 대신에 2개의 집합을 사용한다. 열린 집합(open set)에는 평가를 위한 노드가 포함한다. 노드가 평가를 위해 선택되면 해당 노드는 닫힌 집합(closed set)으로 이동한다. 노드가 닫힌 집합에 있다면 GBFS는 더 이상 그 노드를 조사하지 않는다. 열린 집합이나 닫힌 집합에 있는 노드가 경로상에 있을 거란 보장은 없지만 이 집합들은 불필요한 노드를 쳐내는데 도움이 된다. 열린 집합에서 개발자는 휴리스틱 비용이 가장 적게 드는 노드를 제거한 뒤 이 노드를 테스트하는 작업을 수행한다. 그리고 닫힌 집합은 해당 노드가 닫힌 집합에 속하는지 알아내기 위해 활용된다. 노드가 열린 집합의 멤버인지 또는 닫힌 집합의 멤버인지를 추적하려면 추가 데이터의 이진 값을 사용하면 된다. 그리고 닫힌 집합의 경우에는 노드가 닫힌 집합 소속인지 아닌지 여부만 판별하면 되기 때문에 닫힌 집합을 관리하는 별도의 컬렉션을 사용할 필요는 없다. 열린 집합을 관리하기에 적합한 보편적인 자료 구조는 우선순위 큐이다. 하지만 간결함을 위해 벡터를 사용한다. 벡터를 사용하면 열린 집합에서 가장 낮은 비용을 가진 요소를 찾기 위해 선형 검색을 해야한다. BFS와 마찬가지 이므로 각각의 노드는 GBFS 탐색 동안 노드를 위한 추가 데이터가 필요하다. 추가 데이터의 수가 많으므로 이 데이터를 캡슐화한 구조체를 정의하면 좋다. 가중 그래프를 사용하므로 부모 엣지는 해당 노드로 들어오는 엣지이다. 그리고 각 노드는 자신의 휴리스틱 값과 자신이 열린 집합에 존재하는지 또는 닫힌 집합에 존재하는지를 추적할 수 있어야한다.

struct GBFSScratch {
	const WeightEdge* mParentEdge = nullptr;
    float mHeuristic = 0.0f;
    
    bool mInOpenSet = false;
    bool mInClosedSet = false;
};

그런 다음 키가 노드의 포인터이고 값이 GBFSScratch의 인스턴스인 맵을 정의한다.

using GBFSMap = 
	std::unordered_map<const WeightedGraphNode*, GBFSScratch>

GBFS 함수는 WeightGraph, 시작 노드, 목표 노드 그리고 GBFSMap의 참조를 파라미터로 받는다.

bool GBFS(const WeightedGraph& g, const WeightedGraphNode* start,
			const WeightedGraphNode* goal, GBFSMap& outMap);

GBFS 함수의 시작 부분에 열린 집합 벡터를 정의한다.

std::vector<const WeightedGraphNode*> openSet;

다음으로 평가 중인 노드인 현재 노드를 추적할 변수가 필요하다. 이 현재 노드 변수는 알고리즘이 진행됨에 따라 변경된다. 최초 시작시 현재 노드는 시작 노드이다. 그리고 이 노드는 닫힌 집합에 있다고 표시한다.

const WeightGraphNode* current = start;
outMap[current].mInClosedSet = true;

그리고 GBFS의 메인루프에 진입한다. 먼저 현재 노드와 인접한 노드를 모든 노드를 살펴본다. 메인 루프는 닫힌 집합에 있지 않은 노드만을 고려한다. 이 노드들은 현재 노드로부터 자신의 노드로 향하는 부모 엣지를 가진다. 그리고 코드는 열린 집합에는 없는 노드의 휴리스틱을 계산한 다음, 해당 노드를 열린 집합에 추가한다.

do {
	// 인접 노드를 열린 집합에 추가한다
    for (const WeightEdge* edge : current->mEdges) {
    	// 이 인접 노드의 추가 데이터를 얻는다
        GBFSScratch& data = outMap[edge->mTo];
        // 이 노드가 닫힌 집합에 없다면 추가한다
        if (!data.mInClosedSet) {
        	// 인접 노드의 부모 엣지를 설정
            data.mParentEdge = edge;
            if (!data.mInOpenSet) {
            	// 이 노드의 휴리스틱을 계산하고 열린 집합에 추가한다
                data.mHeuristic = ComputeHeuristic(edge->mTo, goal);
                data.mInOpenSet = true;
                openSet.emplace_back(edge->mTo);
           	}
        }
    }
}

현재 노드에 인접한 노드를 처리한 후에는 열린 집합을 살펴본다. 열린 집합이 비어있다면 평가할 노드가 없다는 것을 뜻한다. 이 경우는 시작점에서 목표점까지의 경로가 존재하지 않을 때 발생한다.

if (openSet.empty()) {
	break;
}

열린 집합에 여전히 노드가 있다면 알고리즘은 계속 진행된다. 열린 집합에서 가장 낮은 휴리스틱 비용을 가진 노드를 찾으면 해당 노드를 닫힌 집합으로 이동해야한다. 이 노드는 새로운 현재 노드가 된다.

// 열린 집합에서 가장 비용이 낮은 노드를 찾자
auto iter = std::min_element(openSet.begin(), openSet.end(),
	[&outMap](const WeightedGraphNode* a, const WeightedGraphNode* b)
    {
    	return outMap[a].mHeuristic < outMap[b].mHeuristic;
    });
// 현재 노드를 설정하고 이 노드를 열린 집합에서 닫힌 집합으로 이동시킨다
current = *iter;
openSet.earse(iter);
outMap[current].mInOpenSet = false;
outMap[current].mInClosedSet = ture;

가장 낮은 휴리스틱 값을 찾기 위해 algorithm 헤더에 있는 std::min_element 함수를 사용했다. 이 함수의 세 번째 파라미터는 한 요소가 다른 요소보다 작은지를 결정하기 위한 방법을 지정하는 특병한 유형의 함수(람다 표현식)를 파라미터로 받는다. min_element 함수는 최솟값을 가진 요소의 반복자를 반환한다. 마지막으로 메인 루프에서는 현재 노드가 목표 노드인지 아닌지를 판단한다.

} while (current != goal);

루프는 위의 while 조건문이 거짓이거나 초기 break 문(열린 집합이 빈 경우)에 걸렸을 때 벗어난다. GBFS가 경로를 발견했는지의 여부는 현재 노드와 목표 노드의 값을 비교하면 된다.

return (current == goal) ? true : false;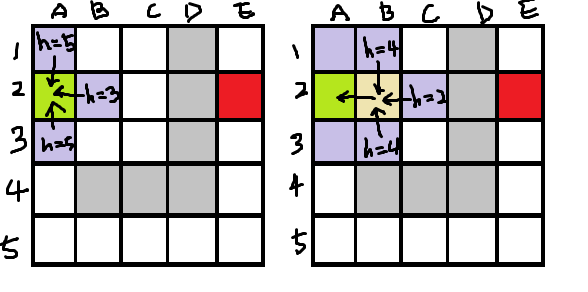

위 그림은 GBFS 루프를 두 번 반복된 상황을 보여준다. 첫 번째 반복이 진행됐을 때 왼쪽처럼 A2가 닫힌 집합에 있고 A2의 인접 노드인 A1, B2, A3의 휴리스틱이 계산되고 열린 집합에 들어간다. 화살의 방향은 자식 노드에서 부모 노드로의 방향이다. 그리고 휴리스틱 비용이 가장 작은 B2가 현재 노드(current)로 바뀌고 닫힌 집합으로 이동한다. 오른쪽은 현재 노드인 B2의 인접 노드들의 휴리스틱을 계산해 열린 집합으로 이동시키는 것을 나타낸다. 여기서는 C2가 가장 낮은 휴리스틱 비용을 갖으므로 C2가 현재 노드가 되고 닫힌 노드로 이동한다. 가장 낮은 휴리스틱 비용을 갖고 있다고 해서 최적의 경로는 아니라는 것을 알 수 있다. 아래 코드는 탐욕 최우선 탐색 함수의 전체 코드이다.

탐욕 최우선 탐색

bool GBFS(const WeightedGraph& g, const WeightedGraphNode* start,
		const WeightedGraphNode* goal, GBFSMap& outMap)
{
	std::vector<const WeightedGraphNode*> openSet;
    // 시작 노드를 현재 노드로 설정하고 닫힌 집합에 있다고 마킹한다
    const WeightGraphNode* current = start;
	outMap[current].mInClosedSet = true;
    do {
		// 인접 노드를 열린 집합에 추가한다
    	for (const WeightEdge* edge : current->mEdges) {
    		// 이 노드의 추가 데이터를 얻는다
        	GBFSScratch& data = outMap[edge->mTo];
       	 	// 닫힌 집합에 있는 노드가 아니라면 테스트 필요
        	if (!data.mInClosedSet) {
        		// 인접 노드의 부모 엣지를 설정한다
            	data.mParentEdge = edge;
            	if (!data.mInOpenSet) {
            		// 이 노드의 휴리스틱을 계산하고 열린 집합에 추가한다
                	data.mHeuristic = ComputeHeuristic(edge->mTo, goal);
                	data.mInOpenSet = true;
                	openSet.emplace_back(edge->mTo);
           		}
        	}
    	}
    
    	if (openSet.empty()) {
		break;
		}
    
    	// 열린 집합에서 가장 비용이 낮은 노드를 찾는다
		auto iter = std::min_element(openSet.begin(), openSet.end(),
			[&outMap](const WeightedGraphNode* a, const WeightedGraphNode* b)
    	{
    		return outMap[a].mHeuristic < outMap[b].mHeuristic;
    	});
    	// 현재 노드로 설정하고 열린 집합에서 닫힌 집합으로 이동시킨다
		current = *iter;
		openSet.earse(iter);
		outMap[current].mInOpenSet = false;
		outMap[current].mInClosedSet = ture;
    } while (current != goal);
    // 경로를 찾았는가?
    return (current == goal) ? true : false;
}