Game Programming in C++ - Day 15

Day 15 3D 그래픽스 - 오브젝트 그리기

3D에서 액터 변환

대부분의 2D 게임은 x가 수평 방향이고 y가 수직 방향인 좌표 시스템을 사용한다. 하지만 2D 좌표 체계에서도 +y는 위나 아래일 수 있으니 좌표 체계는 구현 방법에 의존한다고 볼 수 있다. 세 번째 요소를 더하면 가능한 표현 방법이 증가한다. 임의로 방향을 결정할 수 있지만 한 번 결정하면 일관성을 유지해야한다. 그래서 '+x는 앞으로 +y는 오른쪽으로 +z는 위쪽으로'라고 정했다. 이런 좌표 시스템을 왼손 좌표 시스템(left-hand coordinated system)이라고 부른다. +y가 왼쪽을 향한다면 오른손 좌표 시스템이 될 것이다.

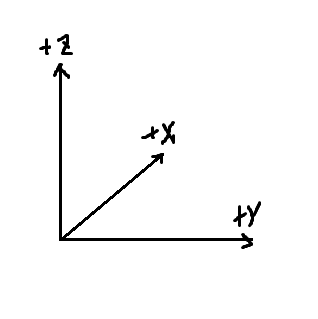
3D를 위한 변환 행렬

3D좌표를 사용하는 것은 동차 좌표가 존재함을 뜻한다$(x, y, z, w)$. 변환 행렬을 구현하기 위해선 w 요소가 필요했다. 3D 좌표에서 변환 행렬은 $4\times 4$ 행렬이 된다. 이러한 수정은 이동과 스케일에 대해서는 간단하다. $4\times 4$ 이동 행렬은 오프셋 $(a, b, c)$로 이동시킨다.

$T(a, b, c)=\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&0&1\\a&b&c&1\\ \end{bmatrix}$

마찬가지로 스케일 행렬은 세 요소를 스케일한다.

$S(s_x, s_y, s_z)=\begin{bmatrix}s_x&0&0&0\\0&s_y&0&0\\0&0&0&s_z\\a&b&c&1\\ \end{bmatrix}$

하지만 3D에서 회전은 단순하지 않다.

오일러 각

3D 상에서 회전을 표현하는 건 2D보다 복잡하다. 2D에서는 액터가 회전에 대해 하나의 float 값만 필요했었다. 2D상에서 회전은 z축에 대한 회전을 표현했던 것이다. 하지만 3D에서는 세 좌표축 전부에서도 회전하는 것이 유효하다. 3D 회전에 대한 접근 방식 중 하나로 오일러 각(Euler angle)이라는 것이 있는데 오일러 각은 각 축에 대한 회전을 표현하는 3가지 용어가 있다(요(yaw), 피치(pitch), 롤(roll)). 요는 상향 축에 대한 회전이며, 피치는 측면 축에 대한 회전이고, 롤은 전방축에 대한 회전이다. 왼손 좌표 시스템에서 요는 +z에 대한 회전이며 피치는 +y에 대한 회전이고 롤은 +x에 대한 회전이다. 3개의 다른 회전 각도인 각각의 오일러 각에 대한 별도의 회전 행렬을 만든 뒤 이 행렬들을 결합하면 최종 회전 행렬을 구하는 것이 가능하다. 이 세 행렬을 곱할 때는 곱셈의 순서가 오브젝트의 최종 회전에 영향을 미친다. 곱셈 순서의 일반적인 접근법은 롤, 피치, 요순으로 곱하는 것이다.

$FinalRot=(RollMatrix)(PitchMatrix)(YawMatrix)$

그러나 오일러 각을 적용하는데 있어 올바른 순서가 없기 때문에 가능한 순서 중 하나를 선택해서 계속 그 순서로 곱을 해줘야한다. 오일러 각을 사용할 때 단점 중 하나는 임의의 회전을 유도하는 것이 어렵다는데 있다. 우주선이 오브젝트 공간에서 +x축을 향하고 있다고 가정하고 우주선을 위치 P에 있는 임의의 오브젝트를 향하도록 회전하길 원한다. 이 새로운 방향을얻기 위해서는 오일러 각에서는 요, 피치, 롤의 결합이 필요하며, 이런 별도의 각을 결합하는 것은 쉽지 않다. 또한 처음에 오일러 각도와 방향을 가진 오브젝트가 있다고 했을 때 이 상황에서 물체가 이동할 때 목표 방향으로 부드럽게 전이하거나 보간하기를 원한다. 각 각도를 별도로 보간한다면 오일러 각도를 보간하는 것이 가능하다. 그러나 여러 상황에서 이런 보간을 올바르게 보이지 않는다. 왜냐하면 각 요소를 별도로 보간하면 보간이 이상한 방향에서 나타나는 특이한 상황과 맞딱뜨릴 수 있기 때문이다. 게임에서 오일러 각을 사용할 수는 있겠지만 임의의 축에 대한 회전에 대해서는 오일러 각보다 더 잘 작동하는 대안이 존재한다.

쿼터니언

수많은 게임은 오일러 각 대신에 쿼터니언(quaternion, 사원수)을 사용한다. 쿼터니언의 공식적인 수학 정의는 복잡하다. 그래서 쿼터니언을 임의의 축에 대한 회전을 나타내는 방법이라고 간단하게 표현한다.

기본 정의
3D 그래픽스는 단위 쿼터니언(unit quaternion)을 사용한다. 단위 쿼터니언은 크기가 1인 쿼터니언이다. 쿼터니어은 벡터와 스칼라 두 요소 모두를 가진다. 이 책에서는 쿼터니언의 벡터와 스칼라 요소를 다음 표기법을 사용해서 표현한다.

$q=[q_v, q_s]

벡터 및 스칼라 요소의 계산은 정규화된 회전 축 $\hat{a}$와 회전 각도 $\theta$에 의존한다.

q_v = $\hat{a}sin{\theta\over 2}$
q_s = $cos{\theta\over 2}$

이 방정식은 정규화된 회전축에서만 잘 작동한다. 정규화되지 않은 축을 위 공식에 적용하면 단위 쿼터니언이 아닌 값을 산출하며, 이는 게임상에서 오브젝트가 찢겨지는 듯한(균일하지 않게 오브젝트가 뻗어나가는 현상) 현상을 유발한다. 오일러 각을 사용해서 우주선을 임의의 오브젝트를 향하도록 회전시키려면 정확한 요, 피치, 롤 각도를 계산해야 하는데 이는 매우 어렵다. 그러나 쿼터니언은 이 문제를 쉽게 해결한다. 초기에 우주선은 x축을 향하고 있으며 위치 S에 있다. 이제 우주선은 임의의 점 P를 향하도록 회전하길 원한다. 먼저 우주선에서 새로운 지점으로의 벡터를 계산한 뒤 이 벡터를 정규화한다.

$NewFacing=\frac{P-S}{\Vert P-S\Vert}$

다음으로 초기에 향한 방향과 대상 물체를 향한 방향의 외적을 통해서 회전축을 계산한다. 그리고 이 벡털르 정규화한다.

$\hat{a}=\frac{\langle1,0,0\rangle\times Newfacing}{\Vert \langle1,0,0\rangle\times Newfacing\Vert}$

다음으로 내적과 아크코사인을 사용해서 회전 각도를 계산한다.

$\theta=arccos(\langle1,0,0\rangle\cdot Newfacing)$

마지막으로 위에서 구한 회전축과 각도를 결합해 점 $P$로 향하는 우주선의 회전을 나타내는 쿼터니언을 생성한다. $P$가 3D 공간상의 어떤 위치에 있다하더라도 이 프로세스는 잘 작동한다. 하지만 새롭게 향하게 될 방향과 원래 향했던 방향이 평행할 경우 외적의 모든 요소가 0인 벡터를 생성한다. 이 벡터는 길이가 0이므로 벡터를 정규화하기 위해 0으로 나누면 회전축이 깨진다. 그러므로 계산을 하는 모든 코드에서는 NewFacing이 최초에 향했던 방향과 평행하지 않음을 검증해야한다. 두 방향이 평행하면 오브젝트는 이미 NewFacing 방향으로 향하고 있음을 뜻한다. 이 경우에 쿼터니언은 항등 쿼터니언이며 회전을 적용할 필요가 없다. 벡터가 서로 반대 방향을 향한다면 상향 벡터를 기준으로 $\pi$ 라디안만큼 회전시켜주면 된다.

회전 결합
쿼터니언의 또 다른 일반 연산 중 하나는 기존 쿼터니언에 추가 회전을 적용하는 것이다. 두 쿼터니언 $p$, $q$가 주어졌을 때 그라스만 곱(Grassmann product)은 대상을 $q$로 회전한 뒤 $p$로 회전시킨다.

$(pq)_v=p_sq_v+q_vp_s+p_v\times q_v$
$(pq)_s=p_sq_s+p_v\cdot q_v$

위 곱셈 식에서 $p$, $q$ 순서대로 있다고 해도 회전은 $q$, $p$ 순서대로 적용된다. 또한 그라스만 곱은 외적을 사용하므로 교환할 수 없다. 그래서 $p$와 $q$의 순서를 바꾸면 회전 순서를 바꾼다. 행렬과 유사하게 쿼터니언은 역 쿼터니언을 가진다. 단위 쿼터니언에서 쿼터니언의 역은 벡터 요소를 반전시키면 된다.

$q^{-1}=[-q_v, q_s]$

역 쿼터니언이 있으므로 다음과 같이 정의된 항등 쿼터니언도 있다.

$i_v=\langle 0, 0, 0\rangle$
$i_s=1$

벡터를 쿼터니언으로 회전시키기
3D 벡터 $v$를 쿼터니언 $q$로 회전시키기 위해 먼저 $v$를 다음처럼 쿼터닝너 $r$로 나타낸다.

$r=[\overrightarrow{v}, 0]$

그리고 두 쿼터니언의 그라스만 곱인 $r^{'}$을 계산한다.

$r^{'}=(qr)q^{-1}$

그러면 회전된 벡터는 쿼터니언 $r^{'}$의 벡터 요소와 같다.

$\overrightarrow{v}^{'}=r_v^{'}$

구면 선형 보간
쿼터니언은 구면 선형 보간(Slerp, Spherical Linear Interpolation)이라는 보다 정확한 보간 형태를 지원한다. Slerp 방정식은 두 쿼터니언 $a$, $b$와 $a$에서 $b$까지의 [0, 1]범위 분수 값을 인자로 받는다. 예를 들어 다음 식은 $a$에서 $b$경로로 25%회전한 쿼터니언을 생성한다.

$Slerp(a,b,0.25)$

쿼터니언을 위한 회전 경로
게임은 세계 변환 행렬을 사용하므로 쿼터니언을 코드에서 사용하려면 회전 행렬로 변환해야한다. 쿼터니언을 행렬로 변환하는 것은 매우 복잡하다.

$q_v=\langle q_x, q_y, q_z\rangle$
$q_s=q_w$
$Rotate(q)=\begin{bmatrix}1-2q_y^2-2q_z^2&2q_xq_y+2q_wq_z&2q_xq_z-2q_wq_y&0\\2q_xq_y-2q_wq_z&1-2q_x^2-2q_z^2&2q_yq_z+2q_wq_x&0\\2q_xq_z+2q_wq_y&2q_yq_z-2q_wq_x&1-2q_x^2-2q_y^2&0\\0&0&0&1\\ \end{bmatrix}$

코드 상의 쿼터니언
쿼터니언의 곱셈 순서는 종종 혼선을 주므로 혼선을 주지 않도록 Math.h 라이브러리에서 곱셈 연산자를 사용하는 대신에 Concatenate 함수를 선언했다. 이 함수는 일반적으로 기대하는 순서로 쿼터니언 인자를 받는다. 그래서 회전 q를 적용한 후 p로 회전할 때의 함수 호출은 다음과 같다.

Quaternion result = Quarternion::Concatenate(q, p);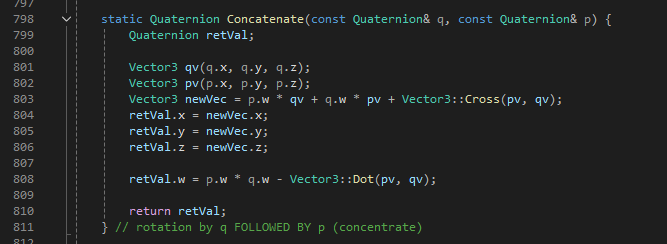

Math.h의 Quaternion 클래스

class Quaternion {
public:
	// 함수/데이터 생략
    // ...
    
    // 축과 각도로부터 쿼터니언 생성
    explicit Quaternion(const Vector3& axis, float angle);
    // 구형 선형 보간
    static Quaternion Slerp(const Quaternion& a, const Quaternion& b, float f);
    // 쿼터니언 곱셈 잇기 (q로 회전한 뒤 p의 회전은 그라스만 곱 pq를 사용한다)
    static Quaternion Concatenate(const Quaternion& q, const Quaternion& p);
    // v = (0, 0, 0); s = 1;
    static const Quaternion Identity;
};
// Matrix4...
// Quaternion에서 Matrix4 생성
static Matrix4 CreateFromQuaternion(const class Quaternion& q);
// Vector3...
// Vector3을 Quaternion으로 변환
static Vector3 Transform(const Vector3& v, const class Quaternion& q);

Matrix4 Matrix4::CreatFromQuaternion(const class Quaternion& q)

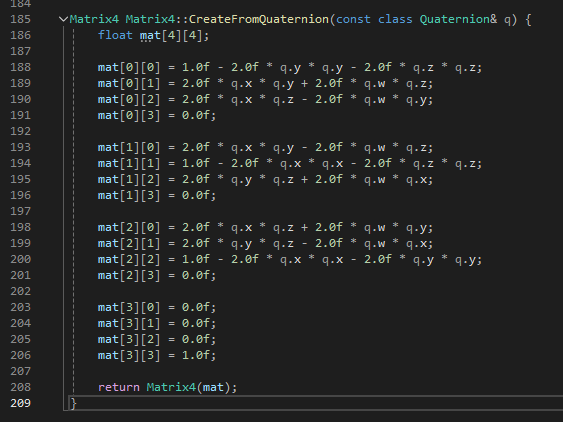
Vector3 Transform(const Vector3& v, const class Quaternion& q)

새로운 액터 변환

Actor 클래스는 이제 위치에 대해서는 Vector3, 회전에 대해서는 Quaternoin, 그리고 스케일에 대해서는 float를 가진다.

Vector3 mPosition;
Quaternion mRotation;
float mScale;

이 새로운 변환을 사용하기 위해 ComputerWorldTransform에서 세계 변환 행렬을 계산하는 코드는 다음과 같이 변경된다.

// 스케일, 회전, 이동
mWorldTransform = Matrix4::CreateScale(mScale);
mWorldTransform *= Matrix4::CreateFromQuaternion(mRotation);
mWorldTransform *= Matrix4::CreateTranslation(mPosition);

그리고 액터의 전방 벡터를 얻으려면 초기 전방 벡터(+$x$)를 회전 쿼터니언으로 변환해야한다.

Vector3 GetForward() const
{
	return Vector3::Transform(Vector3::UnitX, mRotation);
}

그 다음 MoveComponent::Update 함수와 같은, 하나의 각도를 사용해서 회전을 적용했던 코드를 수정해야한다. 지금 MoveComponent는 +z축에 대해서만 회전한다.

void MoveComponent::Update(float deltaTime) {
	if (!Math::NearZero(mAngularSpeed)) {
		Quaternion rot = mOwner->GetRotation();
		float angle = mAngularSpeed * deltaTime;
		// 회전 증가분을 위한 쿼터니언을 생성
		// (상향축을 기준으로회전)
		Quaternion inc(Vector3::UnitZ, angle);
		// 이전 쿼터니언과 새 쿼터니언을 연결한다.
		rot = Quaternion::Concatenate(rot, inc);
		mOwner->SetRotation(rot);
	}
	
    // 전진 속도를 사용한 위치 갱신은 전과 동일
    // ...
}

3D 모델 로딩

스프라이트 기반 게임의 경우 모든 스프라이트 하나의 사각형으로 그리는데, 이는 버텍스 버퍼와 인덱스 버퍼를 하드 코딩해도 별 문제가 되지 않음을 뜻한다. 하지만 3D 게임에서는 다양한 삼각형 메시가 수없이 많다. 예를 들어 FPS 게임에서는 적 메시, 무기 메시, 캐릭터 메시, 환경 메시 등이 있다. 아티스트는 블렌더나 오토데스크, 마야같은 3D 모델링 프로그램으로 이런 모델을 만든다. 게임에서는 이런 모델을 버텍스 및 인덱스 버퍼로 로드하는 코드가 필요하다.

모델 포맷 선택

3D 모델을 사용하려면 먼저 파일에 모델을 저장하는 법을 결정하는 것이 필요하다. 한 가지 방법은 모델링 프로그램을 하나 선택해서 해당 프로그램에 특화된 파일 포맷 로딩을 지원하는 것이다. 3D 모델링 프로그램을 하나 선택해서 해당 프로그램에 특화된 파일 포맷 로딩을 지원하는 것이다. 그러나 이렇게 하면 몇 가지 결점이 존재한다. 3D 모델링 프로그램의 기능 세트는 게임보다 훨씬 많다. 모델링 프로그램은 NURBS, quads, n-gons 등 여러 다른 타입의 지오메트리(geometry)를 지원한다. 또한 모델링 프로그램은 광선 추적(ray racing)을 포함한다. 그리고 복잡한 조명과 렌더링 테크닉을 지원한다. 이런 모든 기능을 게임으로 복제하는 것은 쉽지 않다. 또한 대부분의 모델링 파일은 런타임 때 불필요한 많은 양의 데이터를 가진다. 예를 들면 파일 포맷에는 모델의 실행 취소 기록을 저장할 수도 있다. 이런 추가적인 정보들은 모델링 파일 포맷이 매우 크며, 런타임시 파일을 로딩할때 성능을 떨어뜨린다. 또한 모델링 파일 포맷은 내용이 불분명한 부분이 있으며, 어떤 포맷의 경우에는 문서 자체가 존재하지 않을 수도 있다. 그래서 리버스 엔지니어링을 통해서 파일 포맷을 분석하지 않으면 게임에 파일 포맷을 로드하는 것 자체가 불가능할 수도 있다. 마지막으로 하나의 모델링 포맷을 선택하면 게임은 하나의 특정한 프로그램과 직접적으로 연관된다. 특정 포맷을 사용하면 다른 포맷으로의 변경은 어려워진다. 익스체인지 포맷(exchange format)은 여러 모델링 프로그램에서 동작하는 걸 목표로 한다. 가장 인기 있는 포맷은 FBX와 COLLADA가 있으며, 이런 포맷은 여러 모델링 프로그램이 지원한다. 이런 포맷들을 로딩하기 위한 SDK(software develop kit)이 존재하지만, 여전히 포맷은 런타임 시에 게임에서 필요로 하는 데이터보다 훨씬 많은 데이터를 포함한다. 유니티나 언리얼 엔진 같은 상업용 엔진이 동작하는 방법을 살펴보는 것은 도움이된다. 두 엔진은 자신의 편집기에 FBX와 같은 파일 포맷의 임포트를 지원하지만, 런타임에서는 이 포맷을 사용하지 않는다. 대신에 임포트를 할 때 내부 엔진 포맷으로 변경하는 변환 프로세스가 있다. 이 변환 프로세스를 통해 런타임 시에 게임은 내부 포맷으로 모델을 로드한다. 다른 엔진들은 인기 있는 모델링 프로그램을 위한 익스포트 플로그인을 지원한다. 익스포트 플러그인은 모델링 프로그램의 포맷을 게임 실행시에 사용할 수 있도록 설계된 커스텀 포맷으로 변환한다. Game Programming in C++의 프로젝트에서는 커스텀 파일 포맷을 사용한다. 바이너리 파일 포맷이 보다 효울적이고 대부분의 게임이 바이너리 파일을 사용하지만, 단순성을 위해 JSON 텍스트 파일 포맷을 사용한다. JSON 파일 포맷을 사용하면 수동으로 모델 파일을 쉽게 편집할 수 있므녀, 모델 파일이 적절히 로드됐는지 검증하는 것도 쉽다.

Cube.gpmesh

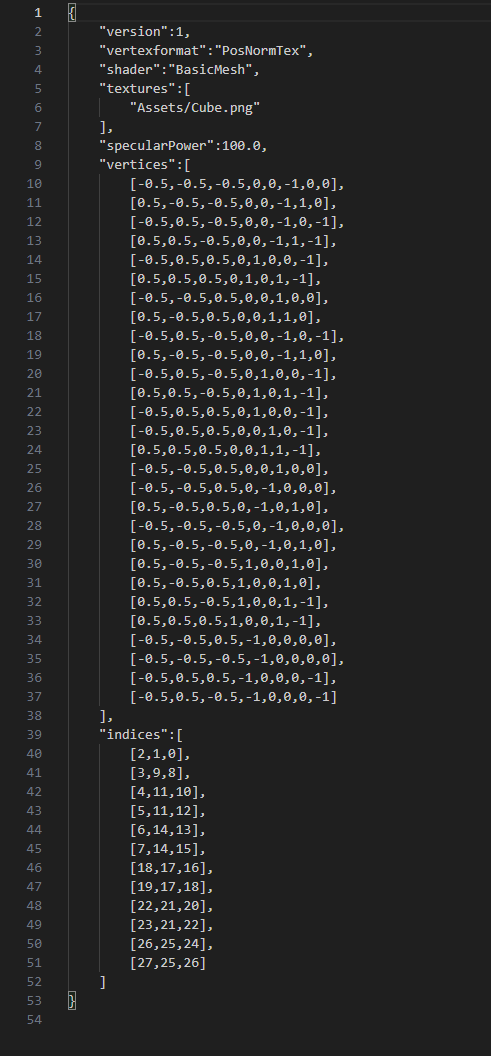
위 파일은 gpmesh 파일 포맷으로 정육면체를 표현했다. 첫 번째 항목은 현재 값이 1인 버전을 지정한다. 다음 줄은 모델에 대한 버텍스 포맷을 지정한다. 버텍스 포맷으로서 위치에 3개의 float 값이 필요했고, 텍스처 좌표에 2개의 float 값이 사용됐는데 여기서 지정된 PosNormTex 포맷은 위치와 텍스처 좌표에 버텍스 법선 벡터를 위한 3개의 float 값을 더 추가했다. 셰이더 항목은 모델을 그린는 데 사용할 셰이더 프로그램을 지정한다. 그리고 텍스처 배열은 모델과 연결된 텍스터 리스트를 지정한다. 마지막 두 항목 버텍스와 인덱스는 모델에 대한 버텍스 버퍼에 인덱스 버퍼를 지정한다. 버텍스의 각 행은 하나의 개별 버텍스이지만, 인덱스의 각 행은 한 개의 삼각형을 뜻한다.

버텍스 속성 갱신

gpmesh 파일이 버텍스당 3개의 버텍스 속성을 사용하므로 지금부터는 모든 메시가 이 포맷을 사용한다고 가정한다. 이 때문에 사각형 메시 또한 법선 벡터가 팔요하다.

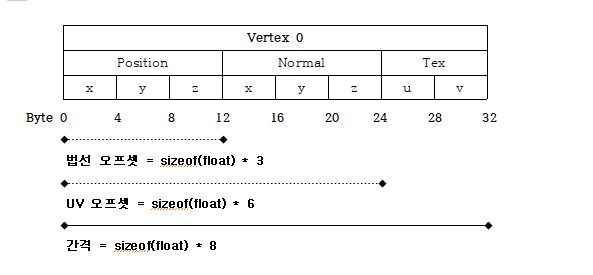
위 그림은 버텍스의 레이아웃을 보여준다. 이제 모든 버텍스 배열은 위 버텍스 레이아웃을 사용할 것이다. 그래서 VertexArray 생성자는 이 새로운 레이아웃을 지정하도록 변경해야한다. 가장 신경 써야 되는 부분은 각 버텍스의 크기가 이제 8 float 이라는 것을 반영하고 법선을 위한 속성을 추가하는 것이다.

// 위치는 3개의 float
glEnableVertexAttribArray(0);
glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 8 * sizeof(float), 0);
// 법선 벡터는 3개의 float
glEnableVertexAttribArray(1);
glVertexAttribPointer(1, 3, GL_FLOAT, GL_FALSE, 8 * sizeof(float), 
	reinterpret_cast<void*>(sizeof(float) * 3));
// 텍스처 좌표는 2개의 float
glEnableVertexAttribArray(2);
glVertexAttribPointer(2, 2, GL_FLOAT, GL_FALSE, 8 * sizeof(float), 
	reinterpret_cast<void*>(sizeof(float) * 6));

그리고 새로운 버텍스 레이아웃을 참조하도록 Sprite.vert도 수정한다.

// 속성 0은 위치, 1은 법선 벡터, 2는 텍스처 좌표다.
layout(location = 0) in vec3 inPosition;
layout(location = 1) in vec3 inNormal;
layout(location = 2) in vec2 inTexCoord;

마지막으로 Game::CreateSpriteVerts에서 생성한 사각형에 법선을 위한 3개의 float을 추가한다. 이렇게 수정하면 스프라이트는 새 버텍스 레이아웃에서도 정상적으로 작동한다.

gpmesh 파일 로딩

gpmesh 포맷은 JSON이며, RapidJSON 라이브러리를 사용해 JSON 포맷을 읽어들인다. Mesh 클래스를 선언해 메시 로딩을 캡슐화한다.

Mesh.h

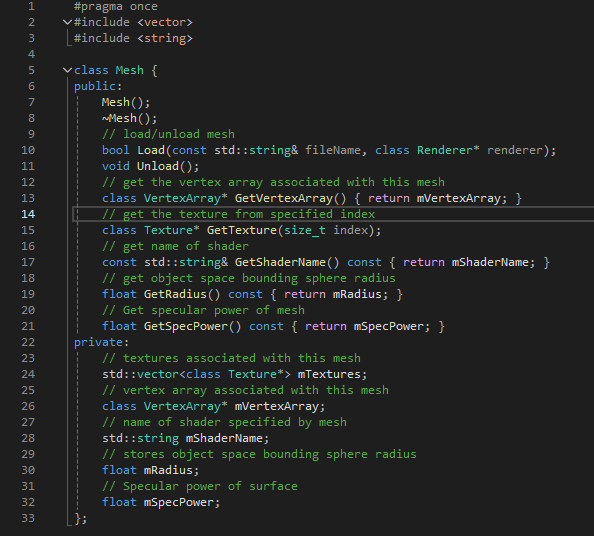
Mesh 클래스에는 Load와 Unload 함수와 생성자와 소멸자가 있다. Mesh의 멤버 데이터에는 텍스처 포인터(gpmesh 파일에서 지정된 각 텍스처에 해당)의 벡터와 VertexArray 포인터(버텍스/인덱스 버퍼용) 그리고 오브젝트 공간에서의 바운딩 구체에 대한 반지름을 포함한다. 이 바운딩 구체의 반지름은 메시 파일을 로드할 때 계산한다. 로드시 반지름을 계산해두면 오브젝트 공간에서의 반지름을 필요로하는 모든 충돌 컴포넌트가 반지름 데이터에 접근할 수 있다. Mesh::Load에서는 2개의 임시 벡터를 만든다. 하나는 버텍스에 관한 것이고, 하나는 모든 인덱스에 관한 것이다. RapidJSON 라이브러리로 모든 값을 읽기를 마치고 난 후 VertexArray 객체를 생성한다. 또한 Game에 로드된 메시 맵과 GetMesh 함수를 만든다. 텍스처와 마찬가지로 GetMesh 함수는 메시가 이미 맵에 있는지를 확인해서 디스크에 메시를 로드해야하 되는지의 여부를 결정한다.

3D 메시 그리기

3D 메시를 로드하고 난 후의 다음 단계는 3D 메시를 그리는 것이다. 그러나 3D 메시를 화면에 그리기 전에 선행돼야 할 많은 주제가 있다. 먼저 Game에서 렌더링에 대한 코드 양이 증가했기 때문에 렌더링과 관련된 코드와 아닌 코드를 분리하기 어려워졌다. 여기다가 3D 메시 그리기 코드를 추가하면 해당 문제가 더 복잡해질 것이다. 이 문제를 해결하고자 모든 렌더링 코드를 캡슐화하는 별도의 Renderer 클래스를 만드는 것이 좋다. 이 코드는 이전에 Game에 있었던 코드와 같은 코드이며, 단지 별도의 클래스로 이동시켰을 뿐이다.

Renderer.h

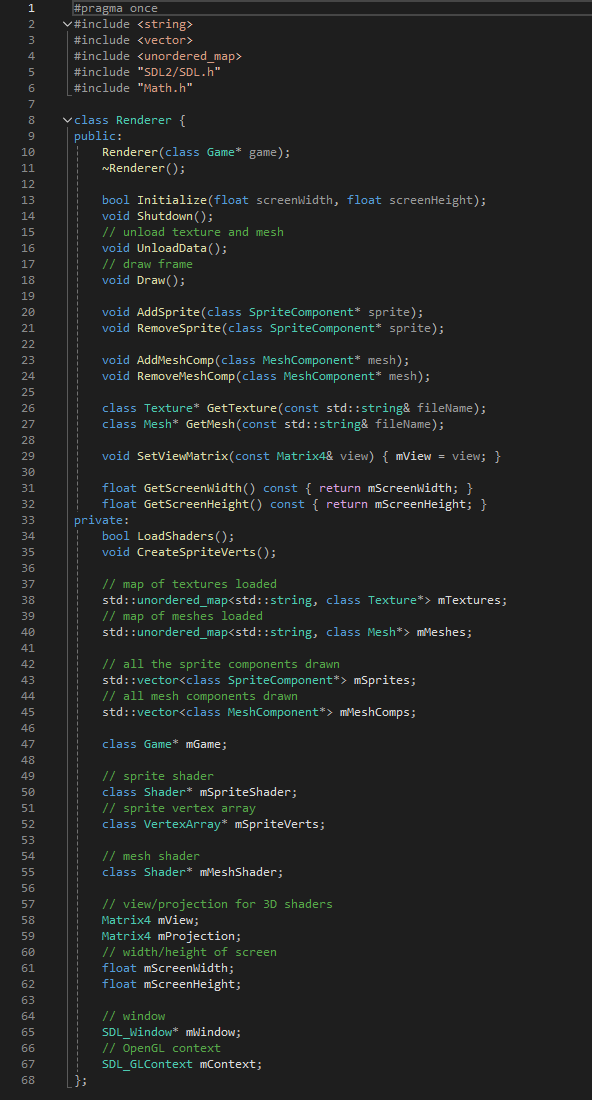
Renderer.cpp

Game 클래스는 Game::Initialize에서 Renderer의 인스턴스를 초기화한다. Initialize함수는 화면의 너비와 높이를 인자로 받고, 이 파라미터를 멤버변수에 저장한다. 그리고 Game::GenerateOutput는 렌더러 인스턴스의 Draw 함수를 호출한다. 로드된 텍스처 맵, 로드된 메시 맵, SpriteComponents에 대한 벡터도 모두 Renderer 클래스로 옮겨야한다. 하지만 이 코드들은 새로운 것이 아니라서 Renderer 클래스로 단순히 이동시켜주기만 하면된다.

클립 공간으로의 변환, 재검토

2D 게임에서는 간단한 뷰-투영 행렬로 세계 공간 좌표를 클립 공간 좌표로 축소했다. 하지만 3D 게임에서는 이러한 타입의 뷰-투영 행렬만으로는 충분하지 않다.대신 뷰-투영 행렬을 별도의 뷰 행렬과 투영 행렬로 분해해야 한다.

뷰 행렬
뷰 행렬(view matrix)은 세계에서 카메라 또는 눈의 위치 및 방향을 나타낸다. 지금은 간단한 카메라를 구현한다. look-at 행렬은 카메라의 위치와 방향을 나타낸다. 일반적으로 look-at 행렬은 카메라의 위치와 방향을 나타낸다.

• 눈의 높이(eye)
• 눈이 바라보는 타겟의 위치(target)
• 눈의 위쪽 방향(up)

이 파라미터들을 이용해서 먼저 4개의 벡터를 계산한다.

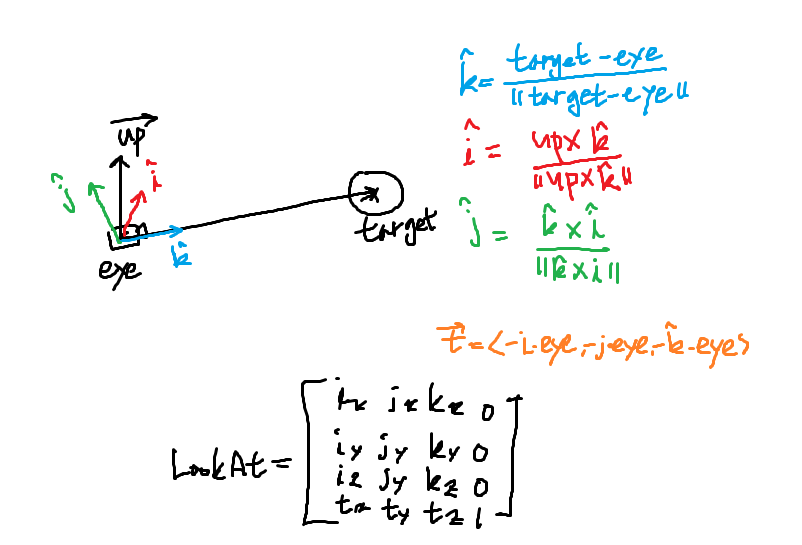
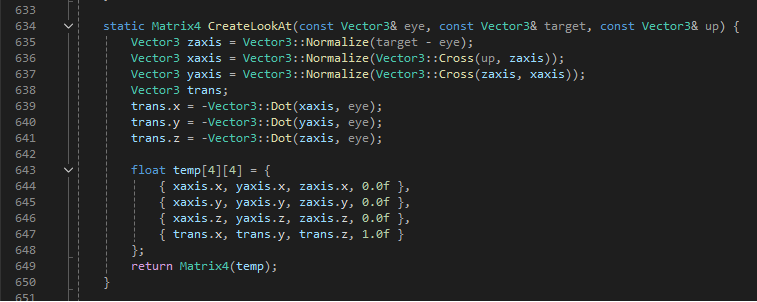
카메라를 이동시키는 빠른 방법은 카메라를 위한 액터를 만드는 것이다. 이 액터의 위치는 눈의 위치를 나타낸다. 그러면 타겟 위치는 카메라 액터의 앞에 있는 어떤 점이 될 것이다. 위쪽 방향은 액터가 뒤집혀지지 않는다면 +z가 될 것이다. 이 파라미터를 Matrix4::CreateLookAt 함수에 전달하면 유효한 뷰 행렬이 된다.

// 카메라 위치
Vector3 eye = mCameraActor->GetPosition();
// 카메라 앞의 10 유닛 떨어진 지점
Vector3 target = mCameraActor->GetPosition() +
	mCameraActor->GetForward() * 10.0f;
Matrix4 view = Matrix4::CreateLookAt(eye, target, Vector3::UintZ);

Matrix4::CreateLookAt

투영 행렬
투영 행렬(projection matrix)은 3D 세계가 화면상의 2D 세계에 그려질 때 평평해지는 정도를 결정한다. 3D 게임에서는 2가지 타입의 투영 행렬이 존재한다.

• 직교 투영(orthographic projection)
• 원근 투영(perspective projection)

직교 투영에서는 카메라에서 멀리 떨어져있는 오브젝트든 가까이에 있는 오브젝트든 그 크기가 같다. 이는 물체가 카메라로 부터 가까이 있는지 멀리 떨어져있는지 플레이어가 지각할 수 없음을 의미한다. 대부분의 2D 게임은 직교 투영을 사용한다.

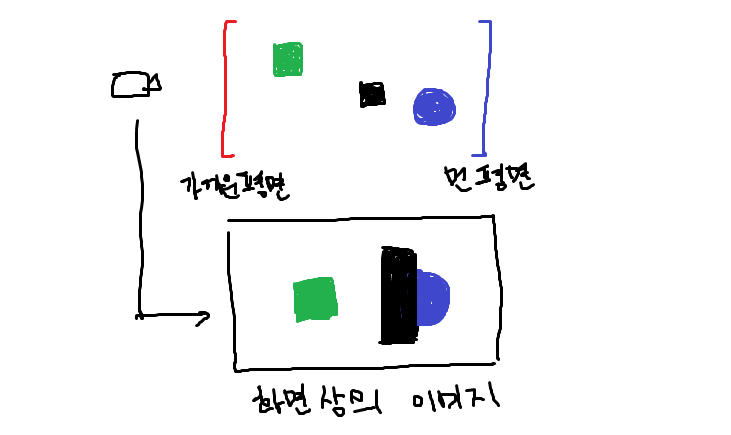
원근 투영에서는 카메라보다 멀리 떨어져 있는 물체는 카메라에 가까이 있는 물체보다 더 작게 보인다. 따라서 플레이어는 화면에 깊이가 있음을 인지한다. 대부분의 3D 게임에서는 이 형태의 투영을 사용한다.

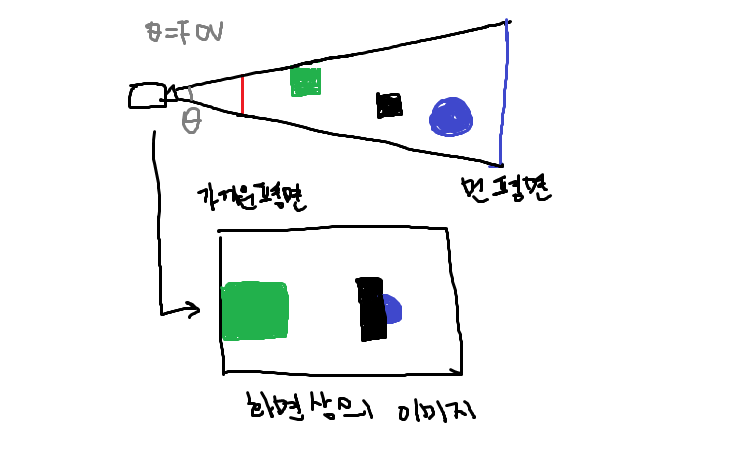
이 각각의 투영은 가까운 평면과 먼 평면을 가진다. 가까운 평면은 일반적으로 카메라에 매우 가깝다. 가메라와 가까운 평면 사이에 있는 모든 물체는 화면 상에 보이지 않는다. 이는 카메라가 너무 가까워지면 게임에서 물체가 부분적으로 사라지는 이유가 된다. 게임은 때때로 플레이어에게 포퍼먼스 향상을 위해 '그려질 부분의 거리'를 줄이는 것을 허용한다. 이를 위해 종종 먼거리의 평면을 당기는 방법을 사용한다. 직교 투영 행렬은 4개의 파라미터가 있다.

• 뷰의 너비
• 뷰의 높이
• 가까운 평면과의 거리
• 먼 평면과의 거리

이 파라미터를 사용해서 직교 투영 행렬을 구성하면 다음과 같다.

$Orthographic=\begin{bmatrix}\frac{2}{width}&0&0&0\\0&\frac{2}{height}&0&0\\0&0&\frac{1}{far-near}&0\\0&0&\frac{near}{far-near}&1\\ \end{bmatrix}$

이 직교 투영 행은 SimpleViewProjection 행렬과 유사하지만 가까운 평면과 먼 평면을 기술하는 추가적인 내용이 있다. 원근 투영은 수평 시야각(FOV, horizontal Field Of View)이라 불리는 추가 파라미터를 가진다. FOV는 투영을 통해 볼 수 있는 카메라의 수평 시야 각도다. 이 FOV, 즉 시야를 변경하면 3D 세계가 눈에 들어오는 범위를 조정할 수 있다. 다음 행렬은 원근 투영 행렬을 보여준다

$yScale=cot(\frac{fov}{2})$
$xScale=yScale\cdot \frac{height}{width}$
$Perspective=\begin{bmatrix}xScale&0&0&0\\0&yScale&0&0\\0&0&\frac{1}{far-near}&0\\0&0&\frac{-near\cdot far}{far-near}&1\\ \end{bmatrix}$

원근 행렬은 동차 좌표의 w 요소를 변경한다. 그리고 원근 나누기(perspective divdie)는 변환된 버텍스의 각 요소를 w요소로 나눈다. 그래서 w 요소는 다시 1이 된다. 이 w로 나누는 연산에 의해 물체가 카메라에서 더 멀리 떨어져 있을수록 물체의 크기는 더 많이 축소된다. OpenGL은 자동으로 장면에 대한 원근 나누기를 수행한다. 두 타입의 투영 행렬은 Math.h 라이브러리에 헬퍼 함수로 구현돼있다. Matrix4::CreateOrtho로 직교 행렬을 생성할 수 있으며. Matrix4CreatePerspectiveFOV을 사용해서 원근 행렬 생성이 가능하다.

뷰-투영 계산하기
뷰-투영 행렬은 뷰와 투영 행렬 간의 단순한 곱이다.

$ViewProjection=(View)(Projection)$

그런 다음 버텍스 셰이더가 세계 공간에서 클립 공간으로 버텍스 위치를 변환하도록 이 뷰-투영 행렬을 사용한다.

Z-버퍼링

화가 알고리즘은 오브젝트를 뒤에서부터 앞으로 그린다는 걸 떠올리자. 이 알고리즘은 2D 게임에는 잘 동작하지만, 3D 게임에서는 복잡성에 직면하게 된다.

화가 알고리즘 블루스
화가 알고리즘의 근본적인 문제점은, 3D 게임에서는 앞뒤 정렬 순서가 정적이지 않다는데 있다. 카메라가 장면을 걸쳐 이동하거나 회전하는 경우 어떤 물체가 앞에 있는지 또는 뒤에 있는지는 매번 변경된다. 3D 장면에서 화가의 알고리즘을 사용하기 위해서는 프레임마다 장면상에 있는 모든 삼각형을 뒤에서부터 앞으로 정렬해야한다. 복잡도가 그렇게 높지 않은 장면에서라도 이 빈번한 정렬한 성능 병목 현상을 초래한다. 화면 분할 게임의 경우에는 이 성능 저하 현상이 더욱더 심각해진다. 예를 들어 플레이어 A와 플레이어 B가 서로 마주본다면 앞뒤 순서는 각 플레이어마다 다르다. 그래서 시점별로 오브젝트를 정렬해야한다. 그리고 화가 알고리즘은 불필요한 대량의 그리기 연산을 수행하고 프레임마다 단일 픽셀에 여러 번 색상을 덮어쓰는 등 많은 문제를 야기한다. 화가의 알고리즘에서는 가까이 있는 물체가 이미 장면에 그려진 물체의 픽셀을 덮어쓰는 경우가 종종 발생하는데 현대의 3D게임에서 픽셀의 최종 색상을 계산하는 과정은 렌더링 파이프라인 과정 중에서 가장 비싼 비용이 드는 부분 중 하나다. 최종 색상 계산에 사용하는 프래그먼트 셰이더에는 텍스처링, 조명 그리고 수많은 여러 고급 테크닉에 관한 코드를 포함하기 떄문이다. 그러므로 3D 게임에서는 가능한 한 픽셀이 다시 그려지는 걸 최대한 제거하는 것을 목표로 한다. 마지막으로 삼각형이 겹치는 문제가 있다.

위 그림에서 어느 삼각형이 더 뒤쪽에 있는가? 정답은 '어떤 삼각형도 뒤에 있지 않다'이다. 이 경우에 화가 알고리즘이 삼각형을 올바르게 그릴 수 있는 유일한 방법은 하나의 삼각형을 절반으로 분할하는 것이지만 좋은 방법은 아니다. 이런 이유로 3D 게임에서는 오브젝트를 그리기 위해 화가의 알고리즘을 사용하지 않는다.

Z 버퍼링(Z-buffering, 깊이 버퍼링)은 렌더링 과정 동안 메모리 버퍼를 추가로 사용한다. z 버퍼(깊이 버퍼)로 알려진 이 버퍼는 장면의 색상 버퍼처럼 각 픽셀에 대한 정보를 저장하는 반면 z 버퍼는 각 픽셀마다 카메라로 부터 거리(깊이)를 저장한다. 색상 버퍼와 z 버퍼, 그리고 다른 버퍼를 포함한 그래픽을 표현할 때 필요한 버퍼 세트를 통칭해서 프레임 퍼버(frame buffer)라고 부른다. 프레임이 시작되면 z 버퍼를 클리어해야한다. z 버퍼는 정규화된 장치의 최대 깊이 값 1.0으로 각 픽셀을 초기화한다. 그리고 렌더링 동안에는 픽셀을 그리기 전에 z 버퍼링은 픽셀의 깊이를 계산한다. 픽셀의 깊이가 z 버퍼에 저장된 현재 깊이 값보다 더 작다면(카메라에 더 가까이 있다면) 해당 픽셀을 색상 버퍼로 그린다. 그러고 나서 z 버퍼는 해당 픽셀의 깊이 값을 갱신한다.

위 그림은 장면에 대한 z 버퍼의 시각적 모습을 보여준다. 앞에서부터 차례대로 구, 원숭이 얼굴, 정육면체가 카메라에 가까이 있으며 z 버퍼의 값이 카메라에 가까울수록 0에 가까우므로 검정색에 가깝다. 프레임에 그려지는 최초의 오브젝트는 항상 자신의 픽셀에 대한 색상과 깊이 정보 모두를 색상 버퍼와 z 버퍼에 모두 기록한다. 그러나 두 번째 오브젝트를 그릴 때는 z 버퍼에 있는값보다 더 0에 가까이 있는 깊이를 가진 픽셀만 그린다. 아래 코드는 z 버퍼링의 의사 코드이다.

// zBuffer[x][y]는 해당 픽셀의 깊이 값을 가진다
foreach MeshComponent m in scene
	foreach Pixel p in m
    	float depth = p.Depth()
        if zBuffer[p.x][p.y] < depth
        	p.draw
        endif
    endfor
endfor

z 버퍼링을 사용하면 장면에서 물체의 순서가 임의로 배치된다 하더라도 물체의 투명도만 없다면 제대로 보인다 하지만 이게 순서는 크게 상관이 없다는 것을 뜻하지 않는다. 예를 들어 장면을 뒤에서부터 앞으로 그리며 화가 알고리즘에서 나타났던 동일한 양의 중복 그리기를 하게된다. 거꾸로 장면을 앞에서부터 뒤로 그리면 중복 그리기는 0이 된다. 하지만 z 버퍼링은 오브젝트별 또는 삼각형에 토대를 둔 것이 아니라 픽셀 단위로 수행되므로 이전에 봤던 겹치는 삼각형에서도 잘 작동한다. z 버퍼링은 더 이상 그래픽 프로그래머가 구현해야할 항목이 아니다. 개발자는 단지 z 버퍼링을 활성화해주기만 하면 된다. OpenGL은 개발자가 최소한의 작업으로 z 버퍼링을 사용할 수 있도록 지원하고 있다. z 버퍼를 사용하려면 먼저 OpenGL 콘텍스트를 생성하기에 앞서 깊이 버퍼를 요청해야한다.

SDL_GL_SetAttribute(SDL_GL_DEPTH_SIZE, 24);

그리고 다음 호출은 깊이 버퍼링을 활성화한다.

glEnable(GL_DEPTH_TEST);

glClear 함수는 깊이 버퍼를 초기화하는데 사용되며, 한 번의 호출을 통해 색상 버퍼와 깊이 버퍼 초기화가 가능하다.

glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

z 버퍼링은 잘 작동하기는 하지만 몇 가지 문제점이 있다. 먼저 투명한 물체에서는 의도한 대로 z 버퍼링이 잘 동작하지 안는다. 게임에 반투명한 물이 있고 이 물 아래에 바위가 있다고 하면, z 버퍼링에서 먼저 수면을 그리면 z 버퍼에 기록이 되며, 바위는 깊이 값이 물보다 더 크기 때문에 그려지지 않는다. 이에 대한 해결책은 불투명한 오브젝트를 z 버퍼를 사용해사 먼저 렌더링하는 것이다. 그런 다음 깊이 버퍼 쓰기를 비활성화하고, 투명한 오브젝트를 뒤에서부터 앞으로 렌더링한다. 픽셀이 렌더링될 때마다 불투명한 오브젝트 너머에 투명한 픽셀은 그려지지 않도록 각 픽셀의 깊이를 테스트해야한다. 투명한 오브젝트를 사용할 때는 화가 알고리즘을 사용해야한다는 걸 의미하지만, 투명한 오브젝트의 수는 그렇게 많지 않을 것이다. 스프라이트 렌더링에서는 투명도가 있는 텍스처를 지원하기 위해 알파 블렌딩을 사용했었다. 이 알파블렌딩은 z 버퍼링과 궁합이 잘 맞지 않으므로 3D 오브젝트에 대한 알파 블렌딩은 비활성화한다. 그리고 스프라이트에만 알파 블렌딩을 재활성화한다. 마찬가지로 스프라이트는 z 버퍼를 비활성화한 후 헨더링해야한다. 이 때문에 렌더링은 두 단계에 걸쳐서 진행된다. 먼저 알파 블렌딩은 비활성화하고 z 버퍼링은 활성화한 후 모든 3D 오브젝트를 렌더링한다. 그리고 모든 스프라이트는 알파 블렌딩을 활성화하고 z 버퍼를 비활성화한 채로 렌더링한다. 이렇게하면 모든 2D 스프라이트는 3D 자면의 제일 앞에 나타난다. 3D 게임은 일반적으로 UI나 HUD 요소를 위해 2D 스프라이트를 사용하므로 이렇게 해도 문제는 없다.

BasicMesh 셰이더

버텍스 레이아웃에 버텍스 법선에 대한 지원을 포함하기 위해 Sprite.vert 셰이더 파일을 수정했었다. 스프라이트 버텍스 셰이더에 대한 이 수정된 코드와 Sprite.frag 셰이더는 완전한 3D 메시에서도 잘 동작한다. 3D 메시의 경우 뷰-투영 행렬 uniform은 다른 값으로 설정되지만, 버텍스/프래그먼트 셰이더 코드는 그대로 유지해도 된다. 즉 BasicMesh.vert/BasicMesh.frag 셰이더 파일은 Sprite.vert/Sprite.frag 셰이더 파일의 단순한 복사본이다. 다음으로 Renderer에 뷰와 투영 행렬을 위한 Matrix4 변수와 메시 셰이더를 위한 Shader* 멤버 변수를 추가한다. 그리고 Renderer::LoadShaders에서 BasicMesh 셰이더를 로드한다. 또한 뷰와 투영 행렬을 초기화한다. 뷰 행렬은 x축을 향하는 look-at 행렬을 초기화하고 투영 행렬은 원근 행렬로 초기화한다.

mMeshShader->SetActive();
// 뷰-투영 행렬 수정
mView = Matrix4::CreateLookAt(
	Vector3::Zero,	// 카메라 위치
    Vector3::UnitX, // 타겟 위치
    Vector3::UnitZ  // 상향 벡터
);
mProjection = Matrix4::CreatePerspectiveFOV(
	Math::ToRadians(70.0f), // 수평 FOV
	mScreenWidth, 			// 뷰의 너비
    mScreenHeight, 			// 뷰의 높이
    25.0f,					// 가까운 평면과의 거리
    10000.0f				// 먼 평면과의 거리
);
mMeshShader->SetMatrixUniform("uViewProj", mView * mProjection);

메시를 위한 셰이더가 있으니 다음 단계는 3D 메시를 그리기 위해 MeshComponent 클래스를 만들어야한다.

MeshComponent 클래스

오브젝트 공간에서 클립 공간으로 버텍스를 변환하는 모든 코드는 버텍스 셰이더에 있다. 각 픽셀의 색상을 채우는 코드는 프래그먼트 셰이더에 있다. 따라서 MeshComponent 클래스는 화면 그리기에 있어 많은 작업을 하지 않는다.

MeshComponent.h

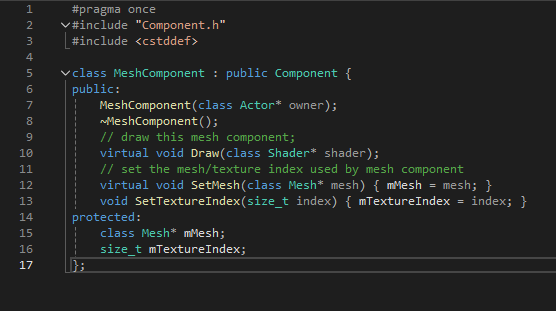
SpriteComponent와 다르게 MeshComponent는 그리기 순서 변수가 없다. 3D 메시 렌더링에서는 z 버퍼링을 사용하므로 순서는 중요하지 않기 때문이다. 유일한 멤버 변수는 텍스처 인덱스와 메시 포인터다. gpmesh는 연관된 텍스처를 여러 개 가질 수 있으며, 인덱스는 MeshComponent를 그릴 때 사용할 특정 텍스처를 결정한다. Renderer는 MeshComponent 포인터에 대한 벡터와 이러한 컴포넌트를 추가하고 제거하는 함수를 가진다. MeshComponent의 생성자와 소멸자에서는 이 Renderer의 추가/삭제 함수를 호출한다.

MeshComponent::Draw

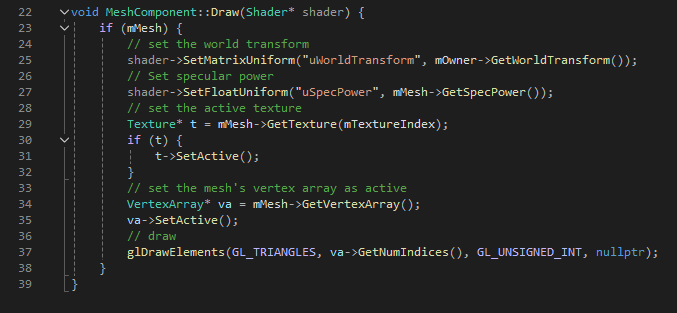
마지막으로 Renderer에는 모든 메시 컴포넌트를 그리는 코드가 필요하다. 프레임 버퍼를 초기화한 후 Renderer는 먼저 깊이 버퍼를 활성화하고 알파 블렌딩은 비활성화한 채로 모든 메시를 그린다. 그 다음에는 모든 스프라이트를 이전과 같은 방식으로 그린다. 모든 것을 그린 후 Renderer는 전면 버퍼와 후면 버퍼를 스왑한다.

// 깊이 버퍼를 활성화하고 알파 블렌딩을 끈다
glEnable(GL_DEPTH_TEST);
glDisable(GL_BLEND);
// 기본 메시 셰이더를 활성화
mMeshShader->SetActive();
// 뷰-투영 행렬 갱신
mMeshShader0>SetMatrixUniform("uViewProj", mView * mProjection);
for (auto mc : mMeshComps) {
	mc->Draw(mMeshShader);
}

MeshComponent는 다른 컴포넌트와 마찬가지로 임의의 액터에 붙어 액터의 메시를 그린다.