Day 16 조명, 퐁 반사와 퐁 셰이딩
조명
메시 프래그먼트 셰이더는 픽셀에 대한 최종 색상으로서 텍스처 색상을 직접 사용했다. 그러나 명암이 존재하지 않는다면 장면은 단조롭게 보인다. 태양이나 전구같은 컨셉트를 근사화하거나 장면에 간단한 다향성을 부여하려면 조명이 필요하다.
버텍스 속성 재검토
조명 메시는 버텍스 위치와 UV 텍스처 좌표를 가진 버텍스 속성보다 더 복잡한 버텍스 속성을 필요로 한다. 조명 메시는 버텍스 법선도 필요하다. 법선은 표면에 수직인 벡터다. 하지만 하나의 점은 표면이 아니다. 그렇다면 이 점에 대한 법선은 어떻게 만들 수 있을까.
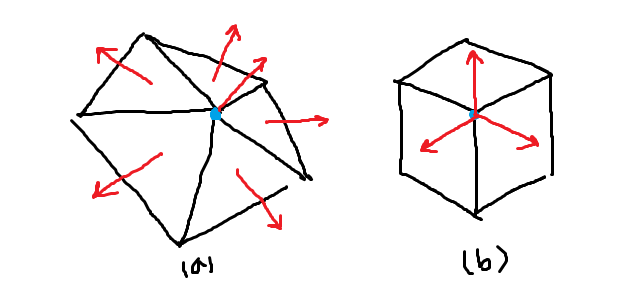
위 그림의 (a)처럼 해당 버텍스를 포함하는 삼각형의 법선들 평균을 구하면 버텍스 법선의 계산이 가능하다. 이 방식은 표면이 부드러운 모델에서는 잘 동작하지만 날카로운 모서리를 가지고 있는 모델에서는 잘 동작하지 않는다. 예를 들어 평균화된 버텍스 법선으로 정육면체를 조명을 적용했을 경우 렌더링하면 정육면체의 구석 부분은 둥글게 나타난다. 이 문제를 해결하려면 아티스트는 정육면체의 구석에 여러 개의 버텍스를 만들고, 버텍스가 다른 법선을 가지도록 제작해야한다. 위 그림의 (b)에서는 그런 방식으로 작성된 정육면체를 보여준다. 프래그먼트 셰이더로 버텍스를 보내면 모든 버텍스 속성이 삼각혀에 걸쳐 보간된다.이는 삼각형의 표면에 있는 임의의 모든 픽셀은 삼각형에 있는 3개의 버텍스 법선들로 보간된 법선 값을 가진다는 걸 뜻한다.
광원의 유형
선택할 수 있는 잠재적인 광원은 많지만, 몇 개의 광원 타입만이 3D 게임상에서 지속적으로 사용된다. 일부 광원은 전체 장면에 영향을 미치지만 다른 광원은 광원 주변에만 영향을 미친다.
주변광
주변광(ambient light)은 장면에서 모든 단일 오브젝트 적용되는 균일한 양의 빛이다. 주변광은 하루 중의 시간에 따라, 게임의 여러 레벨에 따라 다를 수 있다. 밤으로 설정된 레벨은 대낮에 설정된 레벨보다 어둡고 차가울 것이고, 대낮으로 설정된 레벨은 좀 더 밝고 따뜻한 느낌을 가질 것이다. 주변광은 균일한 양을 제공하므로 오브젝트의 여러 면을 다르게 비춰주지 않느다. 즉 주변광은 장면에 있는 모든 물체의 모든 부분에 균일하게 적용되는 전역적인 빛의 양이다. 코드에서 주변광의 가장 간단한 표현은 빛의 색상과 세기를 나타내는 RGB 색상 값이다. 예를 들어 (0.2, 0.2, 0.2)는 (0.5, 0.5, 0.5)보다 어둡다.
방향광
방향광(directional light)은 특정 방향으로 발산하는 빛이다. 주변광처럼 방향광은 전체 장면에 영향을 미친다. 하지만 방향광은 특정 방향에서 오므로 방향광은 물체의 한쪽 측면을 밝혀주지만 다른 측면은 어둡게 남겨둔다. 방향광의 한 예로 날씨가 좋을 때의 태양을 들 수 있다. 빛의 방향은 태양이 그날의 어디에 있는지에 달려 있다. 태양을 마주보는 쪽은 밝지만, 등진 쪽은 어둡다. 방향광을 사용하는 게암은 전체 레벨에서 보통 태양이나 탈을 나타내는 유일한 방향광만을 가진다. 하지만 항상 그렇지만은 않다. 예를 들어 야간의 스포츠 경기장의 광원을 근사하려면 여러 개의 방향광을 사용해야한다. 코드에서 방향광은 RGB 색상값과 빛의 방향을 위한 정규화된 벡터가 필요하다.
점광
점광(point light)는 특정 점에 존재하며 그 점에서 모든 방향으로 빛을 내뿜는다. 점광은 특정 점에서 시작하므로 점광 또한 물체의 한 측면만 밝힌다. 일반적으로 점광은 빛이 도달해서 영행을 미치는 반경을 가진다. 예를 들어 어두운 방에 있는 전구가 있다고 하면 전구 주변에 매우 가까이 있는 영역은 빛이 눈에 보이지만, 거리가 멀어질수록 빛의 세기가 약해서 빛은 점차 소멸한다. 점광은 무한대로 발산하지 않는다. 코드에서 점광은 RGB 색상, 광원의 위치, 광원으로부터 떨어진 거리가 증가할 때 조명값이 얼마나 감소해야 되는지를 결정하는 감쇄(falloff) 반경을 가져야한다.
스포트라이트
스포트라이트(spotlight)는 점광과 유사하지만 점광처럼 모든 방향으로 빛을 내뿜는 대신에 원뿔 형태로 빛을 뿜는다. 스포트라이트를 시뮬레이션하려면 점광의 모든 파라미터외에 추가적으로 원뿔의 각도가 필요하다. 스포트라이트의 전형적인 예는 극장의 스포트라이트와 어둠 속의 플래시 라이트를 들 수 있다.
퐁 반사 모델
광원을 시뮬레이션 하려면 광원과 관련된 데이터가 필요할 뿐만 아니라 광원이 장면에 있는 오브젝트에 얼마나 많은 영향을 미치는지를 계산해야한다. 광원을 근사하는 검증된 방법으로는 양방향 반사도 분포 함수(BRDF, Bidirectional Reflectance Distribution Function)이 있다. BRDF는 빛이 표면에서 반사되는 양을 근사하는 함수다. 여러 유형의 BRDF가 존재하지만 많이 쓰이는 고전적 모델 중 하나로 퐁 반사 모델(Phong reflection model)이 있따. 퐁 모델은 빛의 2차 반사를 계산하지 않으므로 제한된 광원 모델이다. 즉 반사 모델은 각 오브젝트를 전체 장면에서 유일한 오브젝트로 여기고 광원을 비춘다. 현실 세계에서는 흰 벽면에 빨간 빛을 비추면 방의 나머지 부분을 불그스럼한 색으로 채울 것이다. 그러나 이러한 형태는 퐁 모델에서는 일어나지 않는다. 퐁 모델은 빛을 3개의 요소로 구분한다.
- 주변 반사(ambient)
- 난반사(diffuse)
- 정반사(specular)

위 그림은 3가지 요소들을 보여준다. 3가지 요소 모두 표면에 영향을 미치는 빛의 색상뿐만 아니라 포면 색상을 고려한다. 주변 반사 요소(ambient component)는 장면의 전반적인 조명이다. 그러므로 주변 반사 요소는 주변광과 직접 연결하는 것이 좋다. 주변광은 전체 장면에 균등하게 적용되므로 주변 반사 요소는 다른 광원이나 카메라에 대해 독립적이다. 난반사 요소(diffuse component)는 표면으로부터 나오는 빛의 주 반사다. 모든 방향광이나 점광 또는 스포트라이트가 난반사 요소를 결정한다. 난반사 요소 계산에는 표면의 법선 벡터와 표면에서 광원으로의 벡터가 사용된다. 카메라의 위치는 난반사 요소에 영향을 미치지 않는다. 퐁 모델의 마지막 요소는 정반사 요소(specular component)다. 정반사 요소는 표면의 광택을 근사한다. 광택이 나는 금속 물체처럼 높은 반사도를 가진 오브젝트는 광이 나지 않는 검정색으로 채색된 물체보다 더 밝은 하이라이트를 가진다. 난반사 요소처럼 정반사 요소도 광원 벡터와 표면의 법선 벡터에 의존한다. 그러나 반사도는 카메라의 위치에 따라서도 달라진다. 여러 다른 각도에서 광택이 나는 물체를 바라보면 사람이 지각할 수 있는 반사율이 변화하기 때문이다.

위 그림은 측면에서 퐁 반사 모델을 살펴본 것이다. 퐁 반사를 계산하려면 몇몇 변수를 포함한 일련의 계산이 필요하다.
-정규화된 표면 법선 벡터
-표면에서 광원으로의 정규화된 벡터
-표면에서 카메라(눈) 위치로의 정규화된 벡터
-에 대한 -의 정규화된 반사 벡터
-정반사 지수(오브젝트의 광택을 결정)
또한 광원에 대한 색상이 필요하다
- 주변 색상
- 분산 색상
- 반사 색상
퐁 반사 모델에서는 표면에 적용된 광원을 다음과 같이 계산한다.
난반사와 정반사 요소는 장면에 있는 모든 광원을 이용해서 계산하지만 주변 요소는 하나뿐이다. 테스트는 광원이 자신을 마주보는 표면에만 영행을 미침을 보증한다. 여기서 설명한 방정식은 장면의 모든 광원에 대한 색상을 산출한다. 표면의 최종 색상은 표면의 색상과 빛의 색을 곱한 값이다. 광원색과 표면색은 RGB 값이므로 각 요소별 곱셈을 사용한다. 보다 복잡한 구현에서는 표면 색상을 별도의 주변 반사, 난반시, 정반사 색상으로 분리한다. 이 구현에서 방정식은 하나의 곱셈이 아닌, 각각 별도의 색상으로 곱하도록 변경된다. 이제 얼마나 자주 BRDF를 계산할 지가 남아있다. 일반적으로 3가지 방법이 존재한다.
- 표면마다 한 번씩(플랫 셰이딩, flat shading)
- 버텍스마다 한 번씩(고라우드 셰이딩, Goround shading)
- 픽셀마다 한 번씩(퐁 셰이딩, Phong shading)
픽셀당 조명이 계산상으로 더 비싸지만 현대 그래픽 하드웨어는 픽셀당 조명을 쉽게 다룰 수 있다.
조명 구현
주변광과 방향광을 구현하려면 버텍스와 프래그먼트 셰이더의 수정이 필요하다. BasicMesh.vert/.frag 셰이더는 새로운 Phong.vert/.frag 셰이더의 시작점이다. 이 셰이더 코드를 수정해서 모든 메시가 새로운 퐁 셰이더를 사용하도록 변경할 것이다. 조명이 픽셀 단위이므로 퐁 프래그먼스 셰이더는 추가로 몇 개의 uniform이 필요하다.
- 카메라 위치
- 주변광 색상
- 방향광을 위한 몇 개의 변수
// 방향광을 위한 구조체 정의
struct DirectionalLight
{
// 방향광
vec3 mDirection;
// 난반사 색상
vec3 mDiffuseColor;
// 정반사 색상
vec3 mSpecColor;
};
// 조명을 위한 uniform
// 세계 공간에서의 카메라 위치
uniform vec3 uCameraPos;
// 표면에 대한 정반사 지수
uniform float uSpecPower;
// 주변광
uniform vec3 uAmbientLight;
// 방향광(지금은 오직 하나)
uniform DirectionalLight uDirLight;DirectionalLight 구조체 선언을 보면 GLSL은 C/C++처럼 구조체 선언을 지원한다는 것을 알 수 있다. 다음으로 C++로 돌아와서 DirectionalLight에 해당하는 구조체를 선언하고 주변광과 방향광에 대한 두 멤버 변수를 Renderer에 추가한다. glUniform3fv와 glUniform1f 함수는 3D 벡터와 float uniform을 각각 설정한다. Shader에 2개의 새로운 함수 SetVectorUniform과 SetFloatUniform을 만들어서 이 함수들을 호출한다.
void Renderer::SetLightUniforms(Shader* shader) {
// 카메라의 위치는 뷰 행렬의 역행렬에서 구할 수 있다.
Matrix4 invView = mView;
invView.Invert();
shader->SetVectorUniform("uCameraPos", invView.GetTranslation());
// 주변광
shader->SetVectorUniform("uAmbientLight", mAmbientLight);
// 방향광
shader->SetVectorUniform("uDirLight.mDirection", mDirLight.mDirection);
shader->SetVectorUniform("uDirLight.mDiffuseColor", mDirLight.mDiffuseColor);
shader->SetVectorUniform("uDirLight.mSpecColor", mDirLight.mSpecColor);
}함수는 uDirLight 구조체의 특정 멤버를 참조하기 위해 .표기법을 사용한다. 뷰 행렬에서 카메라 위치를 얻어내려면 뷰 행렬의 역행렬을 구해야한다. 역행렬을 구한 후 네 번째 행의 처음 3요소가 카메라의 세계 공간의 위치에 해당한다. 다름으로 gpmesh 파일 포맷을 갱신해서 specularPower 속성을 가진 메시 표면의 정반사 지수(specular power)를 지정한다. 그런 다음 이 속성을 읽어드릴수 있도록 Mesh::Load 코드를 갱신한 뒤 메시를 그리기 전에 MeshComponent::Draw에서 uSpecPower uniform을 설정한다. GLSL로 돌아와서 Phong.vert 버텍스 셰이더는 일부 변경이 필요하다. 카메라 위치와 방향광의 위치는 모두 세계 공간에 있다. 하지만 버텍스 셰이더에서 계산된 gl_Position은 클립 공간에 있다. 표면에서 카메라로 향한느 올바른 벡터를 얻으려면 세계 공간상의 위치가 필요하다. 또한 입력 버텍스 법선은 오브젝트 공간에 있다. 하지만 이 버텍스 법선 또한 세계 공간에서 필요하다. 그래서 버텍스 셰이더는 세계 공간의 법선과 세계 공간의 위치를 계산해서 이 값들을 out 변수를 통해 프래그먼트 셰이더로 보내야한다.
// 세계 공간에서의 법선
out vec3 fragNormal;
// 세계 공간에서의 위치
out vec3 fragWorldPos;그래서 프래그먼트 셰이더의 변수로서 fragNormal과 fragWorldPos를 선언한다.
void main()
{
// 위치를 동차 좌표로 변환
vec4 pos = vec4(inPosition, 1.0);
// 위치를 세계 공간상의 위치로 변환
pos = pos * uWorldTransform;
// 세계 공간상의 위치를 저장
fragWorldPos = pos.xyz;
// 위치를 클립 공간 좌표로 변환
gl_Position = pos * uViewProj;
// 법선을 세계 공간상의 법선으로 변환 (w = 0)
fragNormal = (vec4(inNormal, 0.0f) * uWorldTransform).xyz;
// 텍스처 좌표를 프래그먼트 셰이더로 전달
fragTexCoord = inTexCoord;
}다음으로는 위 코드처럼 fragNormal과 fragWorldPos를 계산한다. swizzle이라고 알려진 .xyz 문법은 4D 벡터에서 x, y, z요소를 추출하고 이 값으로 새로운 3D 벡터를 생성한다. 이 기능은 vec4와 vec3를 효율적으로 변환한다. 또한 법선을 동차 좌표로 변환해서 세계 변환 행렬과 곱셈이 되도록 한다. 그러나 w 요소는 여기서 1이 아니라 0이다. 그 이유는 법선은 위치가 아니라서 법선을 이동시키는 것은 의미가 없기 때문이다. w 요소를 0으로 설정한다는 것은 세계 변환 행렬의 이동 요소가 곱셈으로 인해 0이 된다는 것을 뜻한다.
void main()
{
// 표면 법선
vec3 N = normalize(fragNormal);
// 표면에서 광원으로의 벡터
vec3 L = normalize(-uDirLight.mDirection);
// 표면에서 카메라로 향하는 벡터
vec3 V = normalize(uCameraPos - fragWorldPos);
// N에 대한 -L의 반사
vec3 R = normalize(reflect(-L, N));
// 퐁 반사 계산
vec3 Phong = uAmbientLight;
float NdotL = dot(N, L);
if (NdotL > 0)
{
vec3 Diffuse = uDirLight.mDiffuseColor * NdotL;
vec3 Specular = uDirLight.mSpecColor * pow(max(0.0, dot(R, V)), uSpecPower);
Phong += Diffuse + Specular;
}
// 최종색은 텍스처 색상 곱하기 퐁 광원 (알파값 = 1)
outColor = texture(uTexture, fragTexCoord) * vec4(Phong, 1.0f);
}위 코드는 프래그먼트 셰이더는 이전 절의 방정식에서 설명한 대로 퐁 반사 모델을 계산한다. fragNormal 법선은 정규화된다. OpenGL이 삼각형의 전 표면에 걸쳐 해당 픽셀의 법선 벡터를 얻기 위해 삼각형에 있는 버텍스의 법선 벡터들을 보간한느데, 보간의 각 단계에서 두 정규화된 벡터를 보간할 시 그 결과는 정규화된 벡터를 보장해주지 않기 때문이다. 따라서 보간을 통해 얻은 벡터는 재정규화 되어야한다. 방향광은 한 방향으로 발산하므로 표면에서 광원으로 향하는 벡터는 광원 벡터를 반전시키면 된다. 프래그먼트 셰이더는 몇가지 새로운 GLSL 함수를 사용한다. dot 함수는 내적을 계산하며 reflect는 반사 벡터를 계산한다. max는 두 값 중 최대값을 선택하며 pow는 거듭제곱 값을 계산한다. clamp 함수는 벡터에 전달되 각 요소의 값을 지정된 범위값으로 제한한다. 이번 경우에서 유효한 조명값은 0.0(조명없음)에서부터 1.0(해당 색상의 최대 조명)까지다. 최종 색은 텍스처 색상과 퐁 광원의 곱이다. R과 V의 내적이 음수라면 비정상적인 경우가 발생한다. 이 경우에는 정반사 요소가 음수라서 장면으로부터 빛을 없애버릴 수 있다. max 함수 호출은 내적이 음수라면 0을 선택하기 때문에 이 문제를 막아준다.

위 그림은 구와 정육면체에 퐁 셰이더를 사용해서 광원을 적용한 결과를 보여준다
- 주변광어두운 회색(0.2, 0.2, 0.2)
- 방향광 방향왼쪽 하단(0, -0.7, -0.7)
- 방향광 난반사 색상녹색(0, 1, 0)
- 방향광 정반사 색상밝은 녹색(0.5, 1.0, 0.5)

